Preview
Research Article

Journal of the Korean Society of Combustion. 30 September 2023. 11-19
https://doi.org/10.15231/jksc.2023.28.3.011

Detection of Combustion Instability of Gas Turbine Combustor using Convolutional Autoencoder Model

합성곱 오토인코더 기법을 이용한 가스터빈 연소기의 연소불안정 상태 감지 연구
Junwoo Jung1
,
Daesik Kim1
,
Jaemin Beak1†
정 준우1
,
김 대식1
,
백 재민1†
1Department of Mechanical Engineering, Gangneung-Wonju National University, Korea
1강릉원주대학교 기계공학과
*Corresponding Author

ABSTRACT

This paper presents a method for detecting the system instability in gas turbine combustor. The proposed approach is designed as the convolutional autoencoder technique so that it offers strong attractivity even if it has a very little data. Additionally, given that it is a solution to enhance the learning effect in this system, it also provides convenience of use to practicing engineers. From these benefits, the detection rate of the system instability in the proposed method is improved while in operation, which is compared with that in both a root-mean-square and a zero-crossing approaches as well-known statistic methods.

Keywords
Anomaly detection
Combustion instability
Convolutional autoencoder
Dynamic pressure
Zero crossing rate

MAIN

  • 1. 서 론

  • 2. 연구 방법

  •   2.1 이상 상태 감지 모델

  • 3. 실 험

  •   3.1 합성곱 오토인코더 모델 구성

  •   3.2 가스터빈 연소기 실험

  • 4. 토 론

  •   4.1 하이퍼 파라미터 변화에 대한 영향

  •   4.2 연소불안정 감지 성능 확인

  • 5. 결 론

1. 서 론

최근 산업에서는 친환경적인 요인을 중심으로 가스터빈 연소기를 활용한 작업이 수행되면서, 그에 관한 선진적인 연구 또한 지속적으로 진행되고 있다. 특히, 대표적인 연구 중 하나로써 예혼합 연소 및 수소 혼소 기술은 질소산화물(Nitrogen oxide, NOx)과 온실가스를 줄이고자 개발되었고, 가스터빈 연소기와 관련된 연구 중 가장 주목받는 기술로 잘 알려져 왔다[1,2]. 하지만, 이 기술은 가스터빈 연소기의 화염에서 발생하는 열방출 섭동과 연소실 내부의 압력 섭동이 결합하여 압력 섭동이 증폭되는 연소불안정을 발생시킬 여지가 있으며, 역화 또는 희박화염날림(Lean blow-off)을 연쇄적으로 야기할 수 있다는 문제점을 가지고 있다[3]. 게다가, 산업체 관점에서 연소불안정은 가스터빈 연소기의 안정성을 저하함과 동시에 시스템을 파손시킬 수 있으므로 가장 피해야 할 문제로 지목되어왔다[4].

이러한 문제를 사전에 확인하여 대처하고자, 많은 연구자들은 가스터빈 연소기의 안정성을 판별하는 기술을 개발하는 데 집중해왔다. 개발된 방법 중 하나로써, 제곱-평균-제곱근(Root mean square, RMS) 기반 가스터빈 연소기의 안정성 판별 기술은 동압 신호에 대한 진폭을 시간에 따라 평균화하는 방법으로 정압(Static pressure)의 3~5% 정도 허용 오차를 고려하고 있다[5]. 이 기술은 매우 간결하므로 실무자의 편의를 도모할 수 있다는 큰 장점이 있지만, 가스터빈 연소기 내부에서 발생하는 동압 신호의 진폭만을 고려하기 때문에 시스템이 동작하는 동안 연소불안정을 명확하게 판별하기에는 여간 어려운 일이 아니다. 또 다른 방법 중 하나로써, 시간첨도(Temporal kurtosis, TK) 기술은 시간 영역에서 가스터빈 연소기의 연소불안정을 판별하기 위해 소개되었다[6]. 이 기술은 주어진 동압 신호의 통계적 분포를 통해 가스터빈 연소기의 안정성을 수치화하였으며, TK 값이 3.0 이하로 감소하는 구간을 연소안정 상태에서 연소불안정 상태로 이동하는 천이구간으로 명명함과 동시에 TK 값이 1.5로 수렴하는 구간을 연소불안정 상태라 정의하였다. 게다가, 시간첨도 기술은 간결한 통계적 기법을 활용하므로 연소불안정을 판별하기 위해 쉽게 적용됨과 동시에 실용성 또한 충분히 입증해왔다[7,8]. 다른 연소불안정 판별 기술로써, 영교차율(Zero crossing rate, ZCR) 기반 표준편차 방법은 가스터빈 연소기에서 발생하는 동압 신호의 주기성을 식별하고 정량화하기 위해 제안되었다[9]. 이 방법은 동압 신호의 한 주기에서 0을 교차하는 지점의 수에 따라 연소 상태를 예측하기 때문에 고속 푸리에 변환(Fast fourier transform, FFT)과 같은 복잡한 계산 과정 없이 동압 신호의 주파수를 도출할 수 있으며, RMS 기반 기술과 시간첨도 기술보다 연소불안정을 감지하는 시간을 크게 앞당기는 결과를 도출하였다. 하지만, 앞서 소개한 연소불안정을 판별하는 기술들은 시스템에 대한 정보를 바탕으로 운영되지 않으므로 가스터빈 연소기에 대한 안정성을 지엽적으로 판별할 여지가 있다는 단점을 가진다.

가스터빈 시스템에 대한 정보를 요구하지 않고 가스터빈 연소기의 안정성을 판별하기 위해, 최근에 인공신경망(Neural network, NN) 기술을 기반으로 한 연구들이 활발히 진행되고 있다. 인공신경망에 근간을 둔 연구 중 하나로써, 합성곱 신경망(Convolutional neural network, CNN)과 장단기 메모리(Long short-term memory, LSTM)를 결합하여 연소실 내부에서 촬영된 화염 이미지를 지도 학습하고 가스터빈 연소기의 연소 상태에 대한 안정 및 불안정 상태를 판별하는 방법이 소개되었다[10]. 또한, 고속(Hi- speed) 비디오를 통해 촬영된 연소실 내부의 화염 이미지를 오토인코더(Autoencoder, AE) 기법을 사용하여 학습한 후에 가스터빈 연소기의 안정성을 판별하는 연구를 수행해왔다[11]. 하지만, 이 선행 기술들에 활용된 지도 학습 기반 인공신경망 모델의 경우에는 많은 수의 상태 정보를 가진 데이터를 요구하기 때문에 가스터빈 연소기와 같은 여러 속성의 데이터를 취득하기 어려운 시스템의 경우에는 실제 시스템에 대한 연소불안정을 포괄적으로 판별하기 쉽지 않다. 또한, 가스터빈 연소기에서 데이터를 취득할 수 있는 여건이 될지라도 많은 수의 상태 정보를 가진 데이터에 기반을 둔 학습 기법을 적용하는 것은 적지 않은 시간이 소요되기 때문에 실무자들에게 많은 불편함을 유발할 수 있다.

본 연구에서는 합성곱 오토인코더(Convolutional autoencoder, CAE)에 근간을 두어 가스터빈 연소기의 동압 신호만을 학습하여 연소불안정을 판별하는 방법을 제안한다. 합성곱 오토인코더 방법은 상태 정보가 정의되지 않은 데이터를 사용하더라도 디코더 기법이 내재하므로 본래의 데이터에 대한 특징을 효율적으로 재구성할 수 있는 비지도 학습 기반 인공신경망 기술이다. 이러한 특징을 가졌기에 선행연구들과 달리 훈련 데이터에 대한 종류가 단편적이더라도 학습 결과에 대한 효과를 높일 수 있는 장점이 있다. 또한, 이 방법은 시스템 모델에 대한 학습을 위해 가스터빈 연소기의 화염 이미지가 아닌 동압 신호만을 요구하므로 데이터가 간결할 뿐만 아니라 다른 인공신경망 학습 방법보다 학습 속도가 빠르므로 실무자들에게 편의를 도모할 수 있다. 게다가, 합성곱 오토인코더에 근간을 둔 학습 방법은 시스템의 불확실성 등과 같은 요소에 대해서도 일부 학습이 가능하기에 통계적 방법에 기반으로 한 연소불안정 예측 기술 등 선행 기술들보다 가스터빈 연소기의 연소불안정을 판별하는 시간을 더 단축시킬 수 있다. 본 연구 내용에 대한 성능은 잘 알려진 RMS 기반 기술, 영교차율 기반 표준편차 방법의 성능과 비교하였으며, 비교된 기술들과의 성능 분석은 실제 데이터를 활용한 가스터빈 연소기에 근간을 둔 시뮬레이션을 통해 진행되었다.

본 논문의 나머지 부분은 다음과 같이 구성된다. 2장에서는 합성곱 오토인코더의 개념과 연소불안정을 감지하는 방법에 대해 소개하고, 3장에서는 제안된 합성곱 오토인코더의 모델 구성 및 가스터빈 연소기 실험에 대해 설명한다. 4장에서는 하이퍼 파라미터(Hyper parameter)에 대한 변화에 따른 영향 및 그에 대한 연소불안정 감지 성능을 확인하며, 5장에서는 본 논문의 결과를 요약하여 마무리한다.

2. 연구 방법

2.1 이상 상태 감지 모델

2.1.1 오토인코더 개념

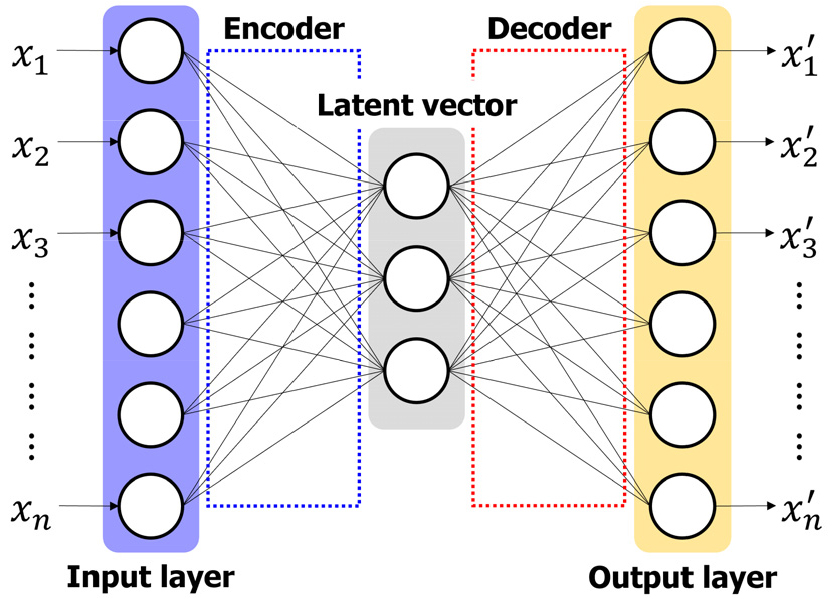
오토인코더는 상태 정보가 정의되지 않은 훈련 데이터를 사용하여 입력 데이터의 특징을 효율적으로 재구성할 수 있는 대표적인 비지도학습 인공 신경망이다[12]. 일반적인 오토인코더는 Fig. 1과 같이 완전 연결 계층(Fully connected layer)의 구조로 이루어진 인코더(Encoder), 잠재 벡터(Latent vector), 그리고 디코더(Decoder)로 구성된다. Fig. 1과 같은 순방향(Feed-forward) 완전 연결 계층의 오토인코더는 계층(Layer)의 수를 증가하거나 잠재 벡터의 크기를 증가시키면 재구성 능력이 향상된다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F1.jpg
Fig. 1.

Configuration of typical autoencoder.

하지만, 시간 의존성(Temporal dependency)을 가진 1차원 시계열 데이터 또는 공간 의존성(Spatial dependency)을 가진 2차원 이미지 데이터에 대한 학습이 어렵다는 단점을 가지고 있다[13]. 따라서, 이를 보완하기 위해 다양한 인공신경망 모델을 활용하여 오토인코더의 구조로 구성하여 사용한다.

2.1.2 합성곱 오토인코더 개념

2.1.1절에서 언급된 오토인코더의 단점을 보완하기 위해 다양한 종류의 오토인코더가 제시되었으며, 그 중 합성곱 신경망을 활용한 합성곱 오토인코더가 많이 활용된다. 합성곱 오토인코더는 합성곱 신경망과 k-means 모델보다 상태 정보가 포함되지 않은 데이터(Unlabeled)에 대한 분류 성능이 효과적인 것을 보였으며, 1-D 신호 정보를 통한 이상 상태 감지에서 뛰어난 성능을 입증한 바가 있다[13,14].

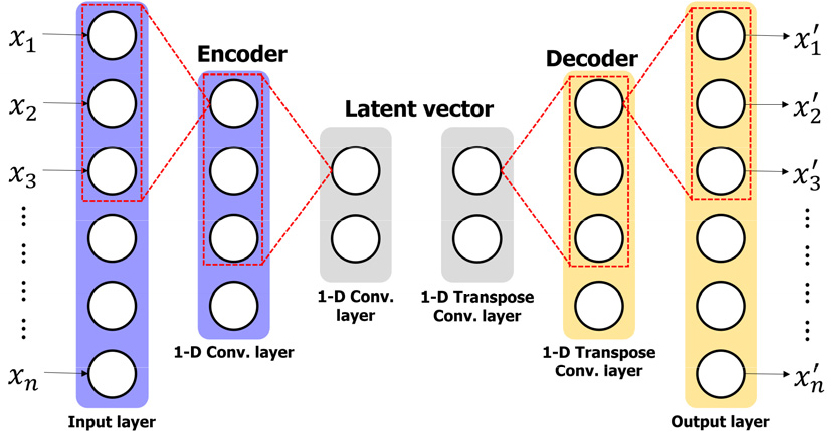
합성곱 오토인코더의 구조는 Fig. 2와 같으며, 오토인코더의 구조와 같이 합성곱 계층(Convolution layer)으로 구성된 인코더 영역과 전치 합성곱 계층(Transpose convolution layer)으로 구성된 디코더 영역으로 나뉜다. 데이터의 정보를 압축하는 인코더의 합성곱 계층의 경우, 아래의 식 (1)로 나타날 수 있다.

(1)
yl+1k=σ(∑xlk⊗wlk+bk)

여기서, xlk와 wlk 는 l번째 계층에서 k번째 특성 지도(Feature map)의 입력 값과 가중치(Weight)를 나타내며, bk는 k번째 특성 맵의 편향 값(Bias)이다. 그리고 ⊗는 합성곱 연산자이며, yl+1k은 합성곱 결과를 의미한다. 𝜎는 활성화 함수를 의미하며, 일반적으로 활성화 함수는 식 (2)으로 표현되는 ReLU(Rectified linear units)을 사용한다.

(2)
σ=max(0,x)

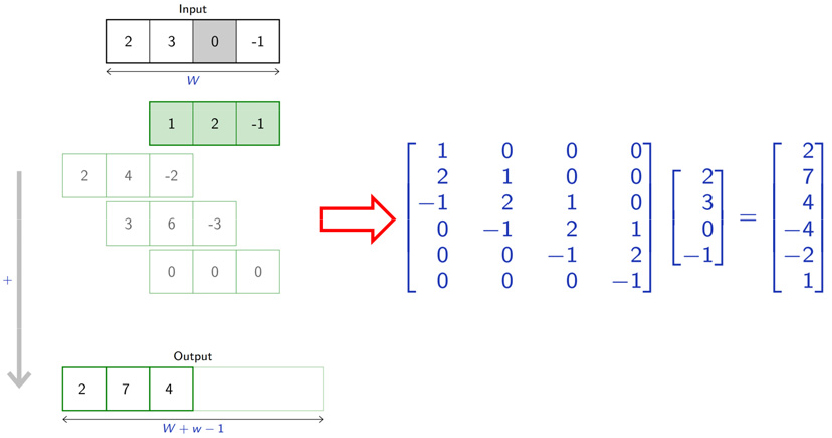
압축된 정보를 재구성하는 디코더의 전치 합성곱 계층은 합성곱 연산을 행렬 표현하였을 때의 커널 행렬을 전치하고, 입력 행렬과 행렬곱을 수행한다. Fig. 3은 1-D 데이터에서의 전치 합성곱 계산을 통해 업샘플링(Upsampling)하는 예시를 나타낸 것이다[15,16].

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F2.jpg
Fig. 2.

Configuration of convolutional autoencoder in 1-D data.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F3.jpg
Fig. 3.

An example for calculation of transpose convolution.

2.1.3 이상 상태 감지 방법

2.1.2절에서 설명된 합성곱 오토인코더를 사용한 이상 상태 감지의 원리는 입력 데이터와 재구성된 출력 데이터 사이의 오차 값 즉, 재구성 데이터 정보의 손실 값을 확인하는 것이다[17]. 정상 데이터로 학습된 합성곱 오토인코더는 입력 데이터로서 정상 데이터를 사용할 경우, 출력 데이터와 입력 데이터 사이의 오차는 적다. 하지만 비정상 데이터를 입력 데이터로써 사용할 경우, 입력 데이터와 출력 데이터 사이의 오차가 크게 발생하여 이상 상태로 감지할 수 있다.

이와 같은 이상 상태 감지 원리를 바탕으로 합성곱 오토인코더는 Table 1과 같이 이상 상태 감지를 수행한다. 먼저, 이상 상태를 감지하기 위해서는 정상 데이터(훈련 데이터)의 집합(N)을 학습한 합성곱 오토인코더 모델(Model)을 사용하여 vk을 출력한다. 그리고 vk와 nk 사이의 오차 값을 계산하여 오차 값 집합(L)에 저장하고, L에서의 최대 오차를 임계 값(t)으로 설정한다. 이때, 본 연구에서 사용된 오차 계산법은 제곱-평균-제곱근 오차(Root mean square error, RMSE)를 사용했다. 다음으로, 감지를 위한 데이터의 집합(D)을 Model의 입력 데이터로 사용하여 출력 데이터(ps)를 생성한다. 이후, ps와 입력 데이터(ds) 사이의 오차 값(es)을 계산한다. 만약 es이 t보다 큰 경우, ds를 이상 상태로 판단하여 이상 상태에 대한 데이터의 집합(A)에 저장한다.

Table 1.

Algorithm of anomaly detection for convolutional autoencoder

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_T1.jpg

3. 실 험

3.1 합성곱 오토인코더 모델 구성

3.1.1 하이퍼 파라미터 설정

본 연구는 Tensorflow 2.9.1 환경[18]에서 합성곱 오토인코더를 구성했다. 합성곱 오토인코더 모델 학습을 위해 사용되는 입력 데이터는 동압 신호 데이터이며, 이는 1차원 형태의 이산 데이터이다. 따라서 합성곱 오토인코더의 계층은 1-D 합성곱 계층으로 구성된다.

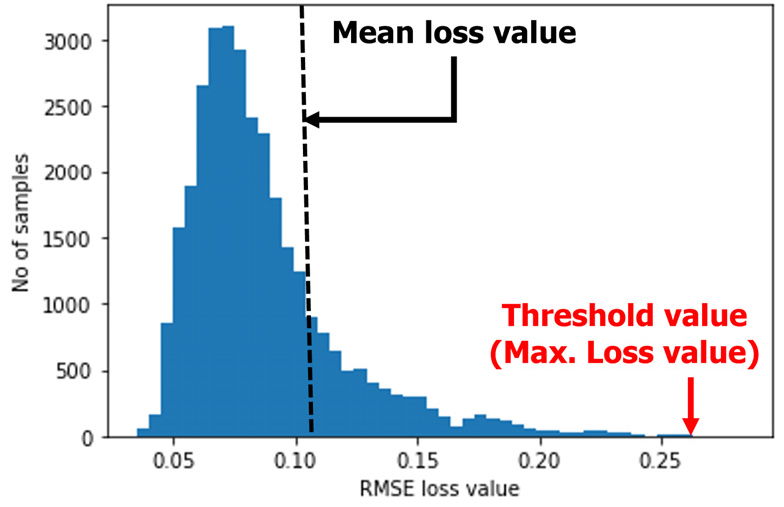
합성곱 오토인코더 구성 시 모델의 구조 변화에 따른 이상 상태 감지 성능 변화를 확인하기 위해 Table 2에 나타난 하이퍼 파라미터를 고정한 상태에서 Table 3와 같이 커널 크기(Kernel size)와 계층의 개수를 변경한 모델들을 만들어 학습을 수행했다. 특히, 각 Model에서 가장 작은 커널 크기를 갖는 잠재 벡터에 대해서는 8과 16의 커널 크기를 적용하여 잠재 벡터의 커널 크기가 모델 성능에 미치는 영향을 확인했다. 그리고 이상 상태 감지 성능의 안정성을 확인하기 위하여 Table 3에 나타난 각 모델에 대해 같은 입력 데이터를 학습한 10개의 모델들을 생성하여 임계 값, 평균 손실(Loss) 값 그리고 감지 시간에 대한 평균과 표준 편차를 확인했다. 여기서 설명되는 임계 값과 평균 손실 값은 Fig. 4를 통해 나타냈다. Fig. 4는 Table 1에서 설명된 오차 값 집합(L)의 히스토그램에 대한 예시를 나타냈으며, 평균 손실 값과 임계 값이 낮은 값을 가질수록 합성곱 오토인코더의 입력 데이터에 대한 재구성 정확도가 높은 것을 의미한다.

Table 2.

Hyper parameters of convolutional autoencoder

Padding Same
Stride 2
Dropout 0.2
Activation Relu
Loss function RMSE
Table 3.

Models of convolutional autoencoder in change of hyper parameters

Model 1 32* → 16 → 8 → 8 → 16 → 32
Model 2 64 → 32 → 16 → 8 → 8 → 16 → 32 → 64
Model 3 128 → 64 → 32 → 16 → 8 → 8 → 16 → 32 → 64 → 128
Model 4 32 → 16 → 16 → 32
Model 5 64 → 32 → 16 → 16 → 32 → 64
Model 6 128 → 64 → 32 → 16 → 16 → 32 → 64 → 128

* Value of kernel size per 1 layer

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F4.jpg
Fig. 4.

An example of histogram for loss values calculated with training data and restructured data (Output data).

게다가, 합성곱 오토인코더 학습과 관련된 하이퍼 파라미터 설정은 학습 속도를 향상하기 위해 Adam(Adaptive moment estimation)을 적용했고, 미니배치 경사 하강법(Minibatch gradient descent)에 대한 에포크(Epoch)는 50 그리고 미니배치 크기는 60으로 설정하였다. 또한, 조기 종료(Early stopping)를 적용하였으며, 조기 종료에 대한 설정값인 인내(Patience) 값을 5로 설정했다.

3.1.2 데이터 전처리 방법

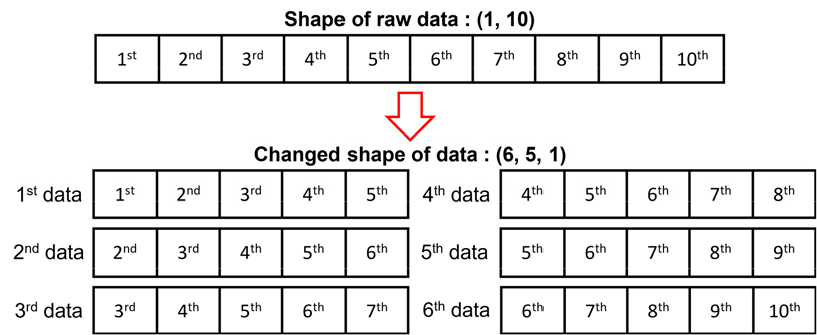
본 연구에서 모델의 입력 데이터로서 단변량 시계열 형태의 동압 신호를 사용하며, 이러한 데이터는 합성곱 오토인코더의 학습을 위해 [배치 크기(Batch size), 시퀀스 길이(Sequence length), 특성(Feature) 개수]로 구성된 3차원의 입력 데이터 형태로 변경된다. Fig. 5의 예시를 통해 3차원 입력 데이터의 형태에 대한 설명을 아래와 같이 나타냈다. 배치 크기는 합성곱 오토인코더 모델에 입력되는 데이터의 수이며, Fig. 5에서 1st data부터 6th data가 입력 데이터를 의미한다. 시퀀스 길이는 데이터 1개 당 포함된 신호의 개수를 의미하며, Fig. 5에서는 시퀀스 길이가 5이다. 특성 개수는 데이터의 종류를 의미하며, 본 연구에서는 동압 신호만을 사용하기 때문에 특성 개수는 1이다. 이러한 3차원 형태의 입력 데이터를 Fig. 5과 같이 각 입력 데이터가 중복되는 신호를 포함되도록 입력 데이터에 대한 전처리를 수행했다. 예를 들어 160,000개의 이산신호 데이터를 시퀀스 길이 100개로 설정하여 데이터 전처리를 수행하면, (159901, 100, 1) 형태의 3차원 입력 데이터로 변경된다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F5.jpg
Fig. 5.

An example for change in shape of input data.

본 연구에서는 1개의 입력 데이터가 가지고 있는 시퀀스의 길이는 모델 학습에 영향을 미치기 때문에 Table 3에서 나타난 모델 구조 변화에 따른 영향을 확인할 때는 시퀀스 길이를 100으로 고정한다. 그리고 모델 구조가 결정된 후 시퀀스 길이를 100~1,000까지 100의 간격으로 감지 결과에 미치는 영향을 확인했다.

마지막으로 모델 학습을 위해 표준 점수(Standard score)를 적용하여 데이터를 정규화했고, 과대 적합을 방지하고자 훈련 데이터의 10%를 검증데이터로 설정하여 합성곱 오토인코더의 학습을 수행했다.

3.1.3 합성곱 오토인코더 학습 결과

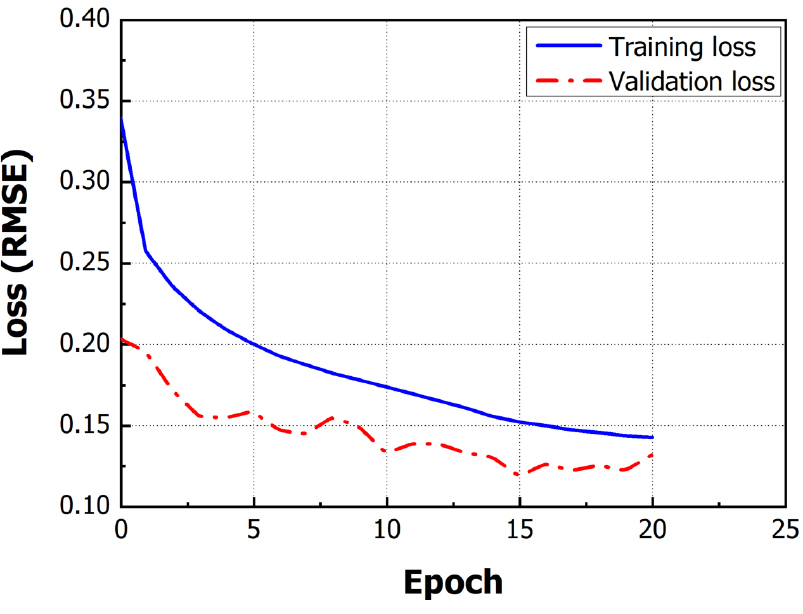
Fig. 6는 3.1.1절과 3.1.2절에서 설명된 설정이 적용된 합성곱 오토인코더의 학습에 대한 훈련 손실(Training loss)과 검증 손실(Validation loss)을 나타낸 그래프이다. Fig. 6에서 확인된 바와 같이 손실 값이 빠르게 감소되어 수렴하는 것이 확인되었다. 또한, 3.1.1절에서 설명된 조기 종료로 인해 설정된 에포크 50이 도달하기 이전에 미리 종료되는 것을 확인되었기 때문에 모델 학습이 성공적으로 수행된 것으로 판단했다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F6.jpg
Fig. 6.

A Graph of training and validation loss per epoch.

3.2 가스터빈 연소기 실험

3.2.1 실험 조건

합성곱 오토인코더의 연소불안정 감지 성능을 확인하기 위해 Joo 등[9]의 연구에서 사용된 예혼합 가스터빈 연소기 실험 결과를 활용했다. 동압 신호 데이터는 덤프면에 위치한 동압 센서로부터 얻어졌으며, 16 kHz의 주파수로 10초 동안 수집되었다. 그리고 연소불안정의 인위적 발생을 위한 운전 조건은 Table 4에 나타냈으며, Initial 조건으로 시작하여 Case 1과 Case 2로 변경했다. 여기서, Case 1은 연료의 조성비를 변경한 조건이며 Case 2는 입열량(Heat input)을 증가한 조건이다. 더 자세한 예혼합 가스터빈 연소기의 실험 장치에 대한 구성과 측정 방법에 대해서는 선행연구[19]에서 확인할 수 있다.

Table 4.

Experimental conditions of combustion state

Name Initial Case 1 Case 2
Combustion state Stable Unstable Unstable
Fuel flow rate [volumetric ratio] H2:CH4 = 87.5:12.5 H2:CH4 = 75:25 H2:CH4 = 87.5:12.5
Overall equivalence ratio 0.51 0.53 0.65
Heat input
[kW] 		40 40 50
Air flow rate [slpm] 1100
Air temperature [℃] 200

본 연구에서는 합성곱 오토인코더의 훈련을 위해 0초부터 2초까지의 동압 신호를 훈련 데이터로 사용했다. 그리고 모델 학습 이후, 0초부터 10초까지의 동압 신호에 대해 연소불안정 감지를 수행하여 합성곱 오토인코더의 성능을 확인했다.

3.2.2 실험 결과

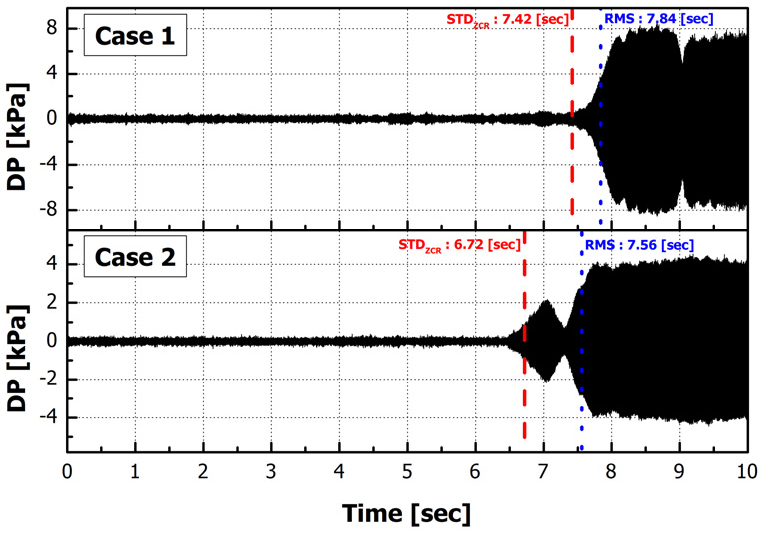
Joo 등[9]은 앞서 설명한 동압 신호 데이터를 바탕으로 영교차율(ZCR)의 표준편차(Standard deviation, STD)를 통해 연소불안정을 감지하는 기법을 제시했다. 그리고 전통적으로 연소불안정 감지를 위해 사용되고 있는 RMS 기반 기술과의 비교를 Fig. 7와 같이 수행하여 제시된 기법에 대한 효과를 확인했다. 따라서 본 연구에서는 Fig. 7에서 제시된 감지 시간과 합성곱 오토인코더를 통해 감지된 시간을 비교하여 연소불안정 감지 성능을 확인했다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F7.jpg
Fig. 7.

Experimental results of detection time between RMS and STDZCR.

4. 토 론

4.1 하이퍼 파라미터 변화에 대한 영향

4.1.1 모델 구조 변화에 대한 영향

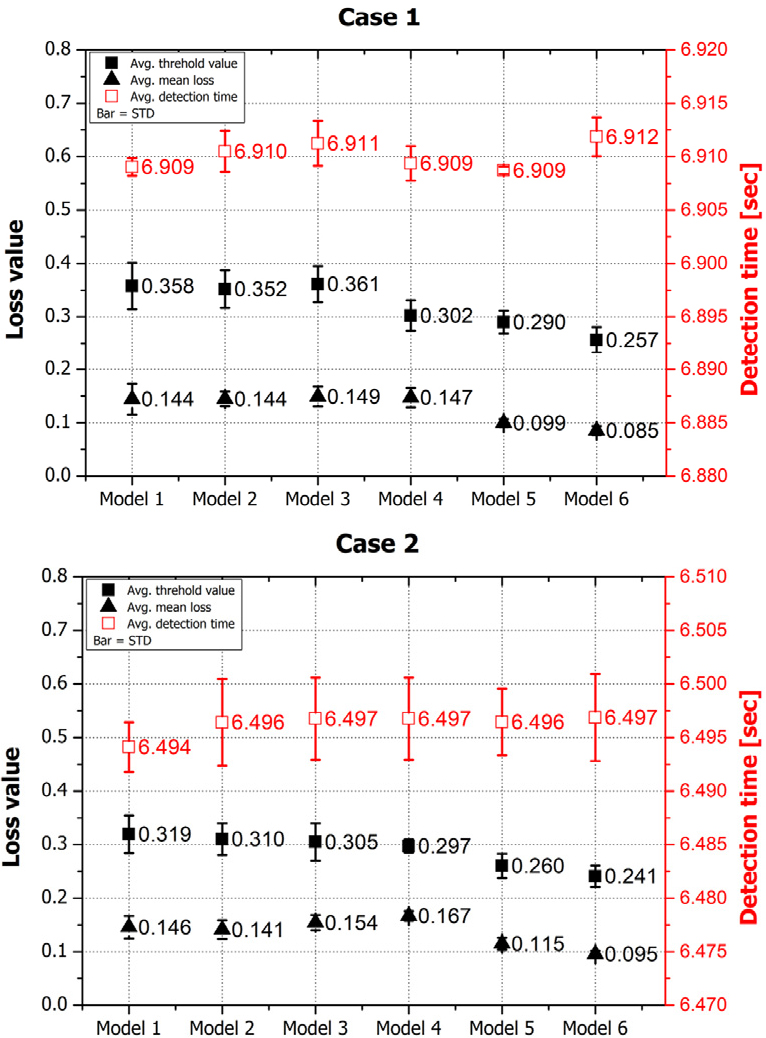
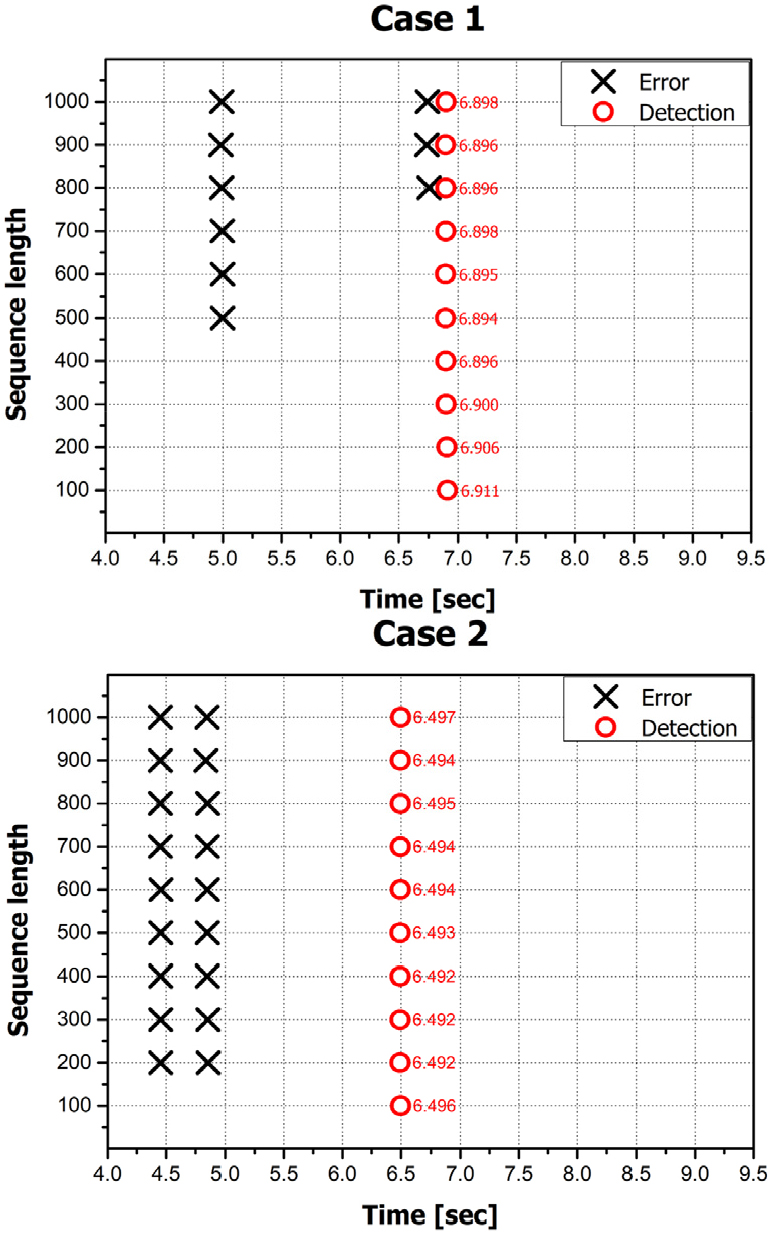
Fig. 8는 Case 1과 Case 2 조건에서 Table 3에 나타난 하이퍼 파라미터의 변화에 따른 감지 시간, 임계 값 그리고 평균 손실 값에 대한 평균과 표준편차를 나타낸 것이다. 모든 모델(Model 1~6)의 평균 감지 시점을 확인했을 때, Case 1은 평균 6.910초에서 감지했고 Case 2는 평균 6.499 초에서 감지했다. 평균 감지 시간과 그에 대한 표준편차를 고려했을 때, 가장 늦게 감지된 시간과 가장 빨리 감지된 시간의 차이가 Case 1은 0.00558초 차이가 발생했으며, Case 2는 0.02859초 차이가 발생한 것을 확인했다. 이를 통해 모델 구조 변화에도 유사한 감지 성능을 보인다는 것을 확인할 수 있다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F8.jpg
Fig. 8.

Average values and standard deviation for detection time of combustion instability, threshold value, and mean loss value in change of hyper parameters at Case 1 and Case 2.

구조 변화에 따른 임계 값과 평균 손실 값을 확인했을 때, 잠재 벡터의 커널 크기가 16인 모델(Model 4~6)이 커널 크기가 8인 모델(Model 1~3)보다 임계 값과 평균 손실 값이 작은 것을 확인할 수 있다. 이는 잠재 벡터의 커널 크기가 증가함에 따라 데이터 정보를 많이 포함하여 재구성을 더욱 정확하게 할 수 있기 때문이다. 계층의 개수 증가에 따른 영향을 볼 때, 잠재 벡터의 커널 크기가 16인 모델이 계층 개수 증가에 따라 임계 값 및 평균 손실 값이 감소하는 것으로 나타났다. 반면, 잠재 벡터의 커널 크기가 8개인 모델은 계층 개수 증가에 따라 임계 값 및 평균 손실 값이 감소하는 효과가 나타나지 않았다. 따라서, 계층의 개수 증가는 반드시 데이터 재구성의 정확도를 증가시키는 것이 아니라는 것을 확인했으며, 일정 수준의 잠재 벡터의 커널 크기가 필요한 것을 확인했다.

본 연구에서는 모든 Model이 유사한 감지 성능을 나타내지만, 임계 값, 평균 손실 값, 그리고 이에 대한 표준 편차가 적게 나타난 Model 6을 기준으로 4.1.2절의 연구를 수행했다.

4.1.2 시퀀스 길이 변화에 대한 영향

3.1.2절에서 언급한 바와 같이 시퀀스 길이는 데이터 하나의 정보 크기를 결정하는 하이퍼 파라미터로써 확인되어야 하는 인자 중 하나이다. Fig. 9는 시퀀스 길이의 변화에 따른 감지 결과를 그래프로 나타낸 것이다. 그 결과, Case 1에서는 시퀀스 길이 100부터 400까지는 정상적으로 연소불안정을 감지했으나, 500부터는 감지 오류가 발생하는 것이 확인되었으며, Case 2에서는 시퀀스 길이 100을 제외한 나머지 시퀀스 길이에서 감지 오류가 발생한 것을 확인했다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F9.jpg
Fig. 9.

Detection time of combustion instability in change of sequence length at Case 1 and Case 2.

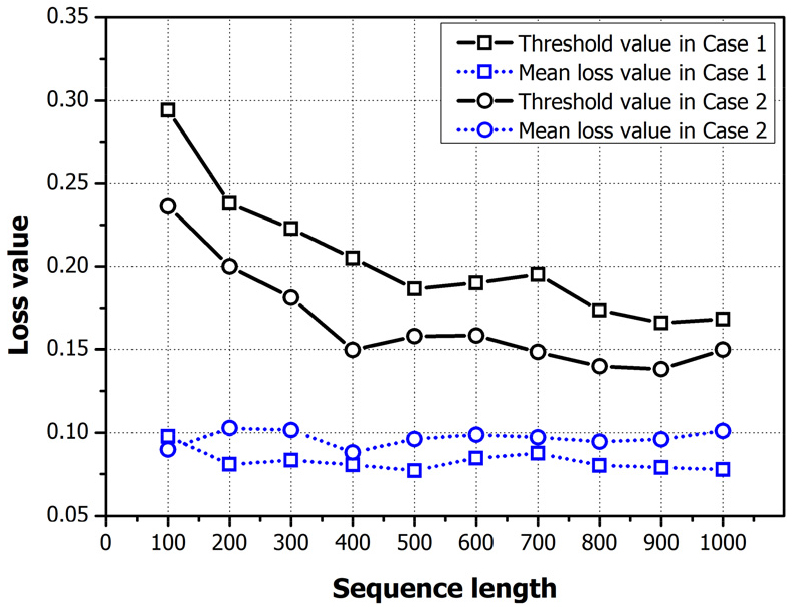
이와 같은 감지 오류의 원인을 확인하기 위해 Fig. 10과 같이 시퀀스 길이 변화에 따른 임계 값 및 평균 손실 값을 확인했다. 평균 손실 값의 경우, 시퀀스 길이 변화에 따른 영향을 보이지 않고 거의 일정한 값을 보였다. 하지만 임계 값의 경우, 시퀀스 길이가 증가함에 따라 감소하는 결과를 나타냈다. 특히, Case 2의 임계 값은 Case 1의 임계 값보다 낮은 값을 보인다. 이러한 임계 값 감소는 입력 데이터의 작은 변화에도 이상 상태로 판단할 수 있는 가능성이 높아짐을 의미한다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F10.jpg
Fig. 10.

Threshold value and mean loss value in change of sequence length at Case 1 and Case 2.

따라서, 시퀀스 길이의 증가로 인해 임계 값이 감소되고, 감소된 임계 값으로 인해 합성곱 오토인코더가 더욱 민감하게 이상 상태를 감지하기 때문에 감지 오류가 나타나는 것을 Fig. 9과 Fig. 10을 통해 확인 가능하다. 또한, 평균 손실의 경우 시퀀스 길이에 의해 영향을 받는 것이 아닌 4.1.1절에서 언급한 바와 같이 모델 구조에 따른 영향을 받는 것을 확인했다.

본 연구는 4.1.1절과 4.1.2절의 결과를 바탕으로 Model 6과 시퀀스 길이 100으로 학습된 합성곱 오토인코더를 사용하여 연소불안정 감지 성능을 4.2절과 같이 확인했다.

4.2 연소불안정 감지 성능 확인

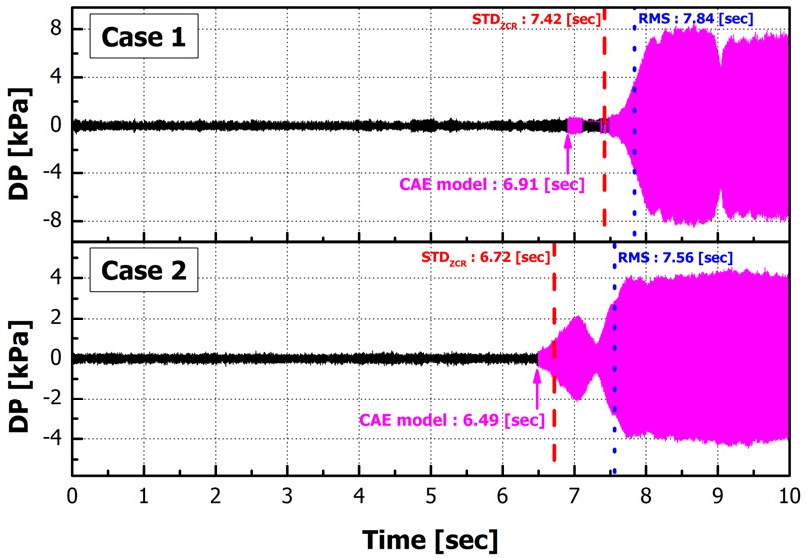
Fig. 11은 Model 6과 시퀀스 길이 100으로 학습된 합성곱 오토인코더에 대한 연소불안정 판단 결과를 나타낸 그래프이다. 합성곱 오토인코더는 Case 1와 Case 2를 각각 6.91초와 6.49초에 연소불안정을 감지했으며, 이는 기존 RMS 기반 기술보다 연소불안정 감지 시간을 약 11.8%와 14.1% 단축한 결과를 보였으며, 영교차율 기반 기술과 비교했을 때, Case 1은 약 6.8% 그리고 Case 2는 3.4% 단축했다. 이때, Fig. 11의 Case 1에서의 결과가 2번의 감지 결과를 나타낸 것을 확인할 수 있다. 이와 같은 감지 결과의 오류 여부를 판단하기 위해 선행연구[9]에서 나타낸 Fig. 12의 결과를 확인했다. Fig. 12에서 약 7초 구간의 STDZCR 값은 연소불안정 판정 기준(CI criterion = 0.003)에 거의 유사한 것을 확인할 수 있으며, 이후 STDZCR 값이 증가하다가 약 7.5초에서 STDZCR 값이 감소되어 연소불안정 판정 기준에 도달한 것을 확인할 수 있다. 이는 Fig. 11의 Case 1에 나타난 합성곱 오토인코더 감지 결과와 같은 결과이다. 따라서, 약 6.9초에서 연소불안정을 감지한 결과가 오류가 아닌 것을 확인했으며 합성곱 오토인코더가 가스터빈 연소기의 동압 신호 데이터만으로 연소불안정을 감지할 수 있다는 결과를 확인했다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F11.jpg
Fig. 11.

Experimental results of detection time between CAE, RMS, and STDZCR at Case 1 and Case 2.

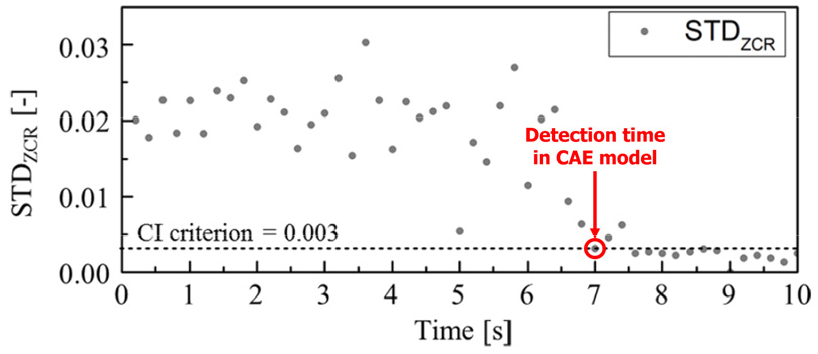
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-03/N0590280302/images/ksssf_28_03_02_F12.jpg
Fig. 12.

Comparison to demonstrate the suitability of experimental result for the STDZCR derived from [9].

5. 결 론

본 논문은 합성곱 오토인코더를 활용하여 가스터빈 연소기의 연소불안정을 감지하는 방법을 제안했다. 본 연구에서 제안된 방법은 기존의 통계적 기법 연구와는 달리 디코더가 내재된 인공신경망 기술에 기반하였기에 가스터빈 연소기의 동압 신호라는 단일 데이터만을 활용할지라도 존재하는 기법들보다 더 간결하면서 빠른 연소불안정을 감지함을 보였다. 제안된 방법에 대한 성능은 시뮬레이션을 통해 확인하였으며, 성능 향상에 대한 검증은 잘 알려진 통계적 기법들의 시뮬레이션 결과와 비교하여 진행되었다.

본 논문에서 소개된 방법은 산업 현장에서 사용되는 가스터빈 연소기에 손쉽게 적용될 수 있으리라 생각되며, 많은 실무자에게 작업의 효율과 안전을 향상시킬 수 있음과 동시에 편의를 제공할 수 있으리라 믿는다.

Acknowledgements

본 연구는 2023년도 정부(교육부)의 재원으로 한국연구재단 기초연구사업의 지원을 받아 수행된 연구이며(No. 2021R1I1A3059648), 2023년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원(20217010100030) 및 2020년도 강릉원주대학교 신임교원 연구비 지원에 의하여 연구되었음.

References

1
J. Beita, M. Talibi, S. Sadasivuni, R. Balachandran, Thermoacoustic instability considerations for high hydrogen combustion in lean premixed gas turbine combustor, Hydrogen, 2 (2021), 33-57. 10.3390/hydrogen2010003
2
D. Kim, Review on the Development Trend of Hydrogen Gas Turbine Combustion Technology, J. Korean Soc. Combust. 24(4) (2019), 1-10. 10.15231/jksc.2019.24.4.001
3
B. Noble, L. Angello, B. Emerson, T. Lieuwen, Advanced gas turbine combustor health monitoring using combustion dynamics data, high pressure condition, 59th ISA POWID/EPRI Symposium (2016).
4
J. Oh, Y. Yoon, Combustion Instability in Gas Turbine Engines, J. Korean Soc. Propulsion Engineers, 12(4) (2008), 63-77.
5
S. Joo, J. Choi, M. Lee, N. Kim, Prognosis of combustion instability in a gas turbine combustor using spectral centroid & spread, Energy, 224 (2021), 120180. 10.1016/j.energy.2021.120180
6
W. Song, D. Cha, Temporal kurtosis of dynamic pressure signal as a quantitative measure of combustion instability, Appl. Therm. Eng. 104 (2016), 577-586. 10.1016/j.applthermaleng.2016.05.094
7
W. Song, D. Cha, Combustion Instability Assessment Using Temporal Kurtosis of Dynamic Pressure Data, The 48th KOSCO Symposium, (2014), 39-41.
8
S. Choi, J. Baek, D. Kim, Early Diagnosis of Combustion Instability Using Statistical Methods, J. Korean Soc. Combust. 27(3) (2022), 1-7. 10.15231/jksc.2022.27.3.001
9
S. Joo, J. Choi, N. Kim, M. Lee, Zero-crossing rate method as an efficient tool for combustion instability diagnosis, Exp. Therm Fluid Sci. 123 (2021), 110340. 10.1016/j.expthermflusci.2020.110340
10
B. Jun, D. Jang, M. Lee, Combustion instability diagnosis using machine learning methodology of high-speed flame images for the safe operation of a gas turbine combustor, Trans. Korean Soc. Mech. Eng. B 45 (2021), 447-458. 10.3795/KSME-B.2021.45.8.447
11
T. Gangopadhyay, V. Ramanan, A. Akintayo, P.K. Boor, S. Sarkar, S.R. Chakravarthy, S. Sarkar, 3D convolutional selective autoencoder for instability detection in combustion systems, Energy and AI 4 (2021), 100067. 10.1016/j.egyai.2021.100067
12
G. Dong, G. Liao, H. Liu, G. Kuang, A review of the autoencoder and its variants: A comparative perspective from target recognition in synthetic-aperture radar images, IEEE GEOSCI REMOTE M 6 (2018), 44-68. 10.1109/MGRS.2018.2853555
13
C. Fan, F. Xiao, Y. Zhao, J. Wang, Analytical investigation of autoencoder based methoeds for unsupervised anomaly detetion in building energy data, Applied Energy 211 (2018), 1123-1135. 10.1016/j.apenergy.2017.12.005
14
G. Lee, M. Jung, M. Song, J. Choo, Unsupervised anomaly detection of the gas turbine operation via convolutional auto-encoder, 2020 IEEE International Conference on Prognostics and Health Management (2020), 19950224. 10.1109/ICPHM49022.2020.9187054
15
F. Fleurt, François Fleuret's deep-learning courses 14x050, the University of Geneva, Switzerland, Available at https://fleuret.org/francois/
16
C. Lee, S. Lee, P. Kim, Fault detection and diagnosis of chain transmission system using convolutional auto-encoder, Trans. the KSNVE 31 (2021), 563-573. 10.5050/KSNVE.2021.31.5.563
17
J. An, S. Cho, Variational autoencoder based anomaly detection using reconstruction probability, SNU Data Mining Center (2015).
18
Tensorflow 2.9.1, Available at https://www.tensorflow.org.
19
S. Joo, S. Kwak, S. Kim, J. Lee, Y. Yoon, High-frequency transition characteristics of synthetic natural gas combustion in gas turbine, Aeronaut. J. 123 (2019), 138-156. 10.1017/aer.2018.150
페이지 상단으로 이동하기