Numerical Aspects of Noise-Induced Dynamics in Continuous Combustion Systems

Minwoo Lee

doi:10.15231/jksc.2023.28.2.067

Preview

Technical Notes

Journal of the Korean Society of Combustion. 30 June 2023. 66-77
https://doi.org/10.15231/jksc.2023.28.2.067

Numerical Aspects of Noise-Induced Dynamics in Continuous Combustion Systems

연속 연소 시스템의 소음 기반 동역학적 거동에 관한 수치적 고찰

Minwoo Lee¹^†

이 민우¹^†

¹Department of Mechanical Engineering, Hanbat National University

¹국립한밭대학교 기계공학과

^{*Corresponding Author}

ABSTRACT

Combustion systems are exposed to intrinsic and extrinsic noise arising from various sources. Contrasting the conventional viewpoint of treating noise as signal contamination, the stochastic effects on combustion systems, namely the noise-induced dynamics (NID), are attracting much attention. This is because noise can alter the system's dynamics from the nonlinear interactions with the reacting flow field. Because such an alteration in combustion dynamics cannot be analyzed in a traditional deterministic framework, many studies have been conducted to quantitatively and qualitatively analyze the noise-driven behaviors in combustion systems. In this paper, review the various types of noise-induced dynamics in continuous combustion systems along with the low-order numerical simulations and summarize how such dynamics are used to analyze the physical nature of the system. Specifically, we investigate the ▲phenomenological aspects of the NID in combustion systems, ▲NID used for the diagnosis of such systems, and ▲system identification of combustion systems using the NID.

Keywords

Noise-induced dynamics

Combustion dynamics

Combustion noise

Stochastic stability

Low-order modeling

MAIN

1. 서 론
2. NID의 현상학적 측면
2.1 트리거링 및 소음 유도 상태 천이
2.2 소음 유도 간헐성 및 플리커링
3. NID 활용 연소 시스템 진단
3.1 감쇠 인자 및 임계 감속 기반 진단
3.2 시계열 특성 변화 기반 진단
4. NID 기반 연소 시스템 모델링
4.1 확률적 공진 및 코히어런스 공진
4.2 NID 기반 시스템 식별 기법
5. 결 론

1. 서 론

로켓과 가스터빈 등의 추진기관, 소각로, 버너 및 보일러를 포함한 대부분의 연속 연소 시스템은 연소과정 중 다양한 출처에서 유래하는 소음에 지속적으로 노출된다. 이러한 소음은 반응 유동장의 유체역학적 불안정성[1], 화학반응 과정에서의 열방출률 섭동[2], 공기역학적 소음[3] 및 공급 계통 불안정성[4] 등의 복합적인 작용으로써 발생하며, 신호 결합 성질 및 주파수 등에서 매우 다양한 소음 양상을 보인다[5]. 유동장에 작용하는 소음은 전통적인 계측·진단의 관점에서 연구자가 계측하고자 하는 신호의 오염원으로서, 최적화 및 잡음 제거 기법을 통해 소음의 영향을 최소화하는 방향의 연구가 지속되어 왔다[6,7,8]. 그러나 소음이 동적 시스템에 미치는 결정론적 영향이 다양한 물리적 시스템에서 관찰되고, 그러한 영향이 시스템에 내재된 동특성에 대한 정보를 제공할 수 있음이 알려짐에 따라[9,10], 연소 시스템의 소음 기반 동역학(Noise-Induced Dynamics, NID)이 주요한 연구 대상으로 관심받고 있다[5]. 본 논문에서는 소음이 연속 연소 시스템의 동적 거동에 미치는 영향을 고찰하고, 이러한 소음 기반 동역학적 특성이 반응 유동의 진단 및 모델링에 활용된 사례를 분석한다. 또한, 소음 기반 동역학적 거동의 각 예시를 저차(low- order) 수치 모델을 활용한 모사 데이터로 수치적으로 재현하며, 이를 통해 향후 다양한 연소 시스템의 개발 및 운용에 기여하고자 한다.

본 기술논문의 구성은 다음과 같다. 아래 2장에서 연소 시스템에 소음이 작용하였을 때 발생할 수 있는 물리적인 현상과 그러한 현상이 발생하는 조건을 저차 수치 모델로부터 얻은 결과와 함께 정리·분석하였다. 이어서, 3장에서는 NID를 활용한 연소 시스템의 진단 기법을 고찰하고, 실제 연소기의 진단 사례를 요약하였다. 나아가 4장에서는 시스템 모델의 구축 및 시스템 변수 추출에 NID가 어떻게 활용되었는지 정리하였으며, NID에 관한 사례연구 및 수치해석을 통해 얻은 결론을 5장에 기술하였다.

2. NID의 현상학적 측면

2.1 트리거링 및 소음 유도 상태 천이

연소 시스템에서 소음이 유발하는 대표적인 동적 변화는 안정 상태에서 연소 불안정으로의 트리거링(triggering) 현상이 있다. 익히 알려진 바와 같이 연소 불안정은 열방출률 섭동과 음향 섭동의 상호 양성 피드백에 의해 발생하며[11], 흔히 열음향 진동자가 호프 분기(Hopf bifurcation) 이후에 선형 안정성(linear stability)을 상실하며 나타나는 한계 순환(limit cycle)으로 설명된다[12]. 시스템의 비선형적 특성에 따라 이러한 호프 분기는 초임계(supercritical)와 준임계(subcritical)의 두 형태로 나타난다[13]. 초임계 호프 분기 전후의 연소 시스템에서는 연소 불안정이 반드시 분기점(bifurcation point) 이후에만 발생하므로, 분기점 이전의 시스템에 소음이 작용하더라도 소음의 세기 및 특성과 무관하게 시스템은 열음향적으로 안정 상태에 존재하며, 연소 불안정 현상이 발생하지 않는다[5]. 반면에 연소 시스템이 준임계 호프 분기 이전에 존재하는 경우, 선형적으로 안정하더라도 비선형적인 불안정성으로 인해 열음향 섭동이 발생할 수 있다. 이때, 시스템의 비선형성으로 인해 열음향적 안정 상태와 한계 순환 상태가 모두 관찰되는 쌍안정(bistable) 구간이 호프 분기 이전에 존재한다. 호프 분기 인근에서 시간에 따른 섭동 진폭의 변화를 나타내는 표준형(normal form)의 실수 부분은 다음과 같으며:

(1)

\frac{d a}{d t} = a (ϵ + α_{1} | a |^{2} + α_{2} | a |^{4} + \dots),

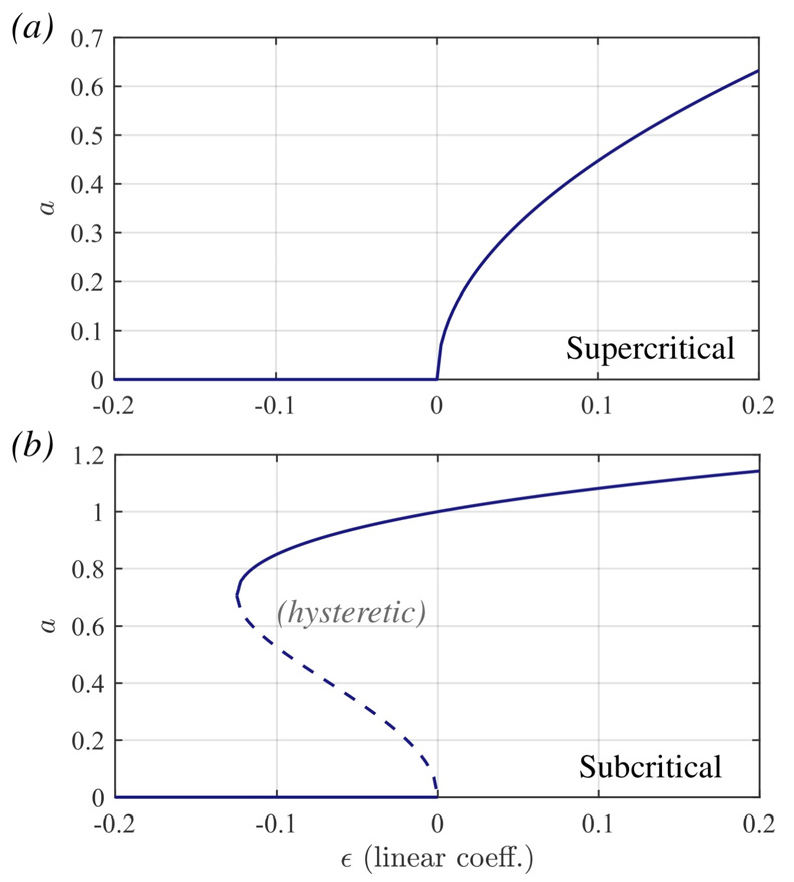
여기서 a는 섭동의 진폭, t는 시간, ε은 분기 인자로 기능하는 선형 변수, α_n은 비선형 변수이다. 선형 변수가 음에서 양으로 변화할 때 호프 분기가 발생하는데, 모든 비선형 항이 음수일 경우 초임계 분기(Fig. 1a)가, 양의 비선형 항이 존재할 경우 준임계 분기(Fig. 1b)가 나타난다. 즉, 준임계 호프 분기에서는 선형적으로 안정한 구간(𝜖)에서도 비선형적인 불안정성( $α_{n} > 0$ )으로 인해 불안정한 한계 순환이 발생할 수 있는 것이다. 이 구간에서 소음이 없는 경우 안정 상태의 시스템은 자발적으로 한계 순환 상태로 발달하지 않으나, 일정 세기 이상의 외란이 가해질 경우 한계 순환, 즉 열음향적 자려진동(self-sustained oscillation) 상태로 발달하게 된다[14]. 이렇게 쌍안정 구간에서 소음으로 인해 연소 불안정이 유도되는 현상이 트리거링이며, 이는 소음으로 인한 상태 천이(noise-induced transition)의 한 형태로서 정의되고 있다[15].

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F1.jpg

Fig. 1.

Illustration of (a) supercritical and (b) subcritical Hopf bifurcation. These figures are obtained by analytically solving Eq. 1 with varying 𝜖 and fixed $α_{n}$ : (a) $α_{1} = - 2$ , $α_{2} = 0$ , and (b) $α_{1} = 2$ , $α_{2} = - 4$ . Both x- and y-axis parameters are in arbitrary units.

호프 분기 인근에 작용하는 소음의 영향은 Eq. 1과 동치인 자려진동 모델, 즉 반 데르 폴(Van der Pol) 진동자에 소음항을 추가함으로써 모사할 수 있다:

(2)

\frac{d^{2} x}{d t^{2}} - (ϵ + α_{1} x^{2} + α_{2} x^{4} + \dots) \frac{d x}{d t} + x = \sqrt{2 d η} .

위의 확률 미분방정식(stochastic differential equation)에서 x는 단위 각주파수( $ω = 1$ )로 진동하는 시스템 변수이며, 진폭 a와 위상 𝜙를 가진 정현파 형태로 표현될 수 있다( $x = a \cos (t + ϕ)$ ). 𝜂는 단위 가우스 잡음(Gaussian noise)이며, d는 이 소음의 세기이다. 선형 변수의 절대값( $| ϵ |$ )이 충분히 작은 경우, 무소음 상태( $d$ =0)에서 Eq. 2를 a에 대해 전개하면 Eq. 1과 동치가 되므로, 호프 분기 인근의 소음 영향을 Eq. 2를 활용하여 효과적으로 모사할 수 있다. 상술한 바와 같이 열음향적 섭동이 호프 분기를 통한 한계 순환의 발생으로 이해되므로, Eq. 2는 열음향 불안정성의 발생 한계 부근에서 연소 시스템의 동적 특성을 나타내는 주요한 현상학적 모델로서 효과적으로 활용되어왔다[12,16,17]. 이러한 모델에서 Eq. 2의 시스템 변수( $x$ )는 압력 섭동을 나타내는 값으로 설정되며, 압력 섭동 진폭( $a$ )을 기준으로 열음향 분기 여부를 판단하게 된다.

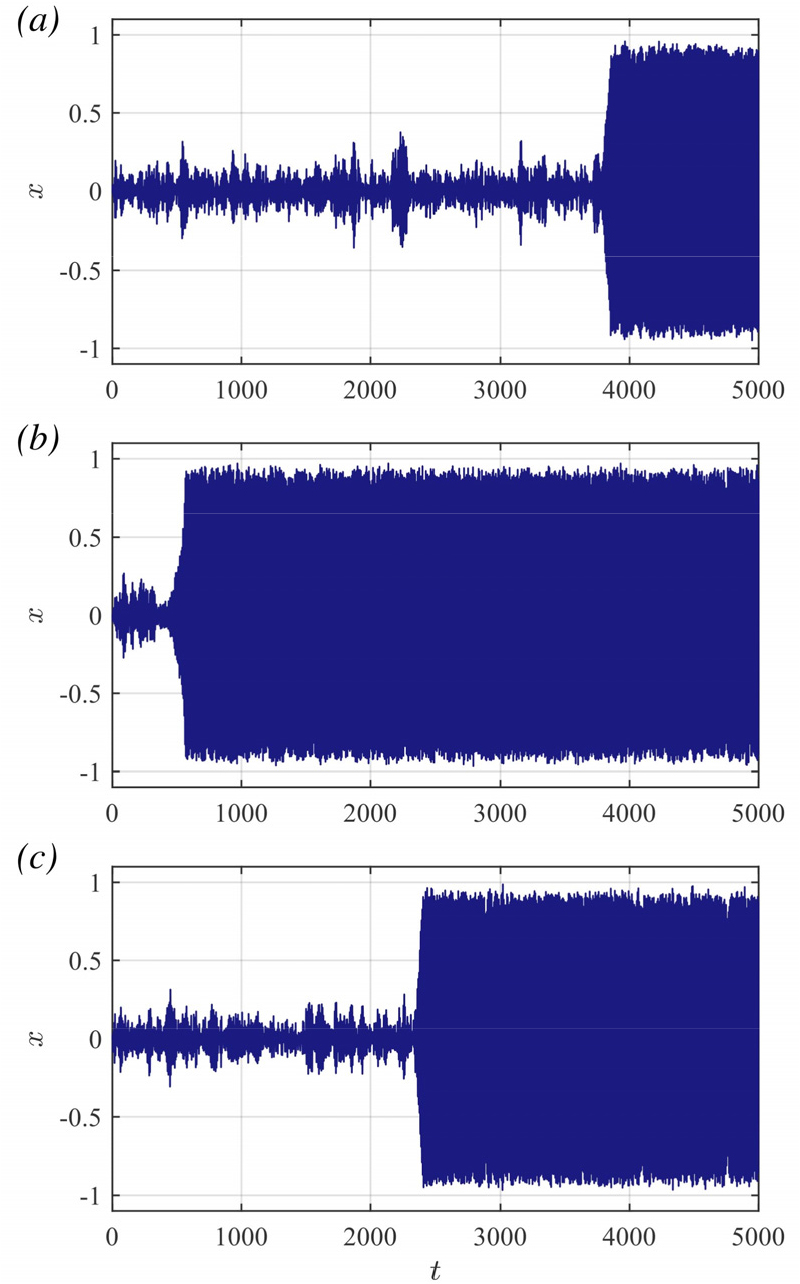
준임계 호프 분기 인근에서 트리거링이 발생하는 경우 작은 소음에 의해서도 신호가 분기 이후에 나타나는 한계순환 형태로 천이한다. 이러한 천이는 Fig. 2와 같이 확률적으로 발생하므로 시간 축에서 트리거링의 시점을 예측할 수 없으나, 발생 빈도에 대한 수치적인 평가는 가능하다. 구체적으로, 시스템이 선형 한계 부근( $| ϵ | \approx 0$ )에 근접할수록 점차 선형 안정성이 낮아지므로, 트리거링이 보다 잘 발생하게 되어 안정 상태의 유지가 어려워진다. 시스템에 작용하는 소음이 강할수록 이와 같은 원리로 트리거링이 쉽게 발생하므로, 소음의 증가는 Fig. 3과 같이 실질적인 쌍안정 구간의 감소로 이어진다. 참고적으로, Fig. 2, 3과 같이 본 논문에서 NID에 관한 고찰을 위해 사용된 데이터는 Eq. 2의 확률 미분방정식을 4차 룬게-쿠타(Runge- Kutta) 방법으로 0.01의 시간 차분을 통해 임의의 시간까지 시간 전진(time marching)한 수치해로부터 획득하였다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F2.jpg

Fig. 2.

Numerical examples of randomly triggered signals near a subcritical Hopf bifurcation. Data in these figures are obtained by numerically solving Eq. 2 with $ϵ = - 0.08$ , $α_{1} = 2$ , $α_{2} = - 4$ , and $d = 5 \times 10^{- 4}$ . Both x- and y-axis parameters are in arbitrary units.

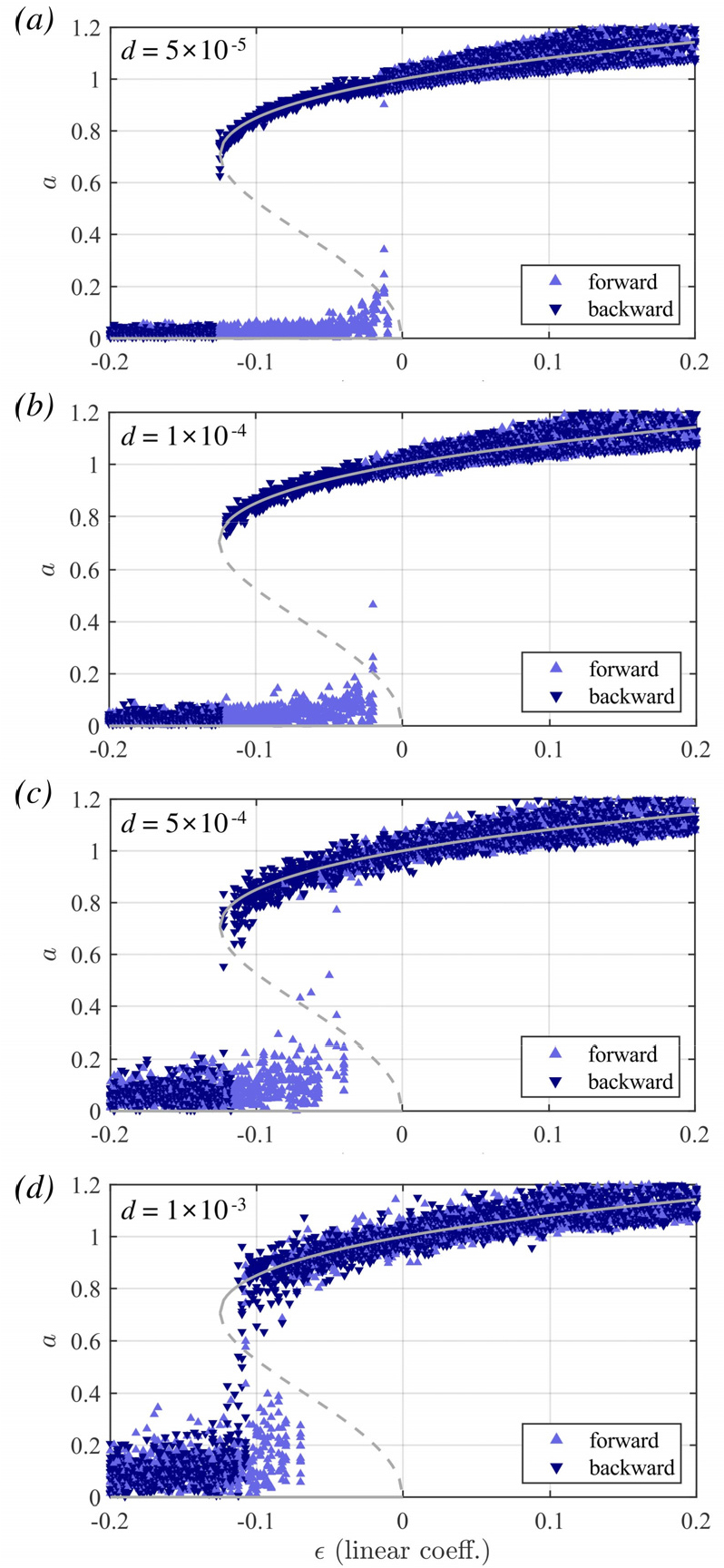
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F3.jpg

Fig. 3.

Illustration of the shrinking bistable region upon increasing noise amplitude d. Triangular markers show the oscillation amplitude (a) obtained from the Hilbert transform of the system signal x (initial transient removed). Gray solid lines show analytically computed oscillation amplitude at zero-noise conditions. Numerical Results are obtained by solving Eq. 2 with $α_{1} = 2$ , $α_{2} = - 4$ , and varying 𝜖. The initial value of x is set to zero (forward) and one (backward). Both x- and y-axis parameters are in arbitrary units.

수학적 관점에서, 연소기에서의 트리거링 현상은 열음향 시스템이 가지는 비정규성(non -normality)으로 인하여 발생하는 것으로 설명된 바 있다[18]. 즉, 고유벡터 간 직교성(orthogonality)이 성립하지 않는 경우 시스템에 작용하는 작은 외란이 증폭되므로, 유동장의 에너지에 비해 미미한 세기의 소음으로도 열음향적 자려진동이 유도되어 연소 불안정 상태로 천이할 수 있는 것이다. 열음향 시스템의 비정규성은 수치적, 실험적 연구에서 모두 관찰되어[18,19] 트리거링의 주요한 수학적 메커니즘으로 이해되고 있다[20]. 선형적으로 안정한 시스템에서 이러한 비정규성으로 인해 작은 불안정성이 크게 증폭되는 현상은 유동이 층류에서 난류로 발달하는 경로 중 하나인 난류 바이패스 천이(bypass transition in turbulence)의 메커니즘으로도 알려져 있는데[21], 이와 같은 상사성을 바탕으로 트리거링의 발생 과정을 분석하는 연구도 수행된 바 있다[11,20]. 이를 통해 층류[20] 및 난류[21] 연소장에서 외란 발생, 외란의 증폭 및 포화, 고진폭 한계순환의 발달과 같은 트리거링 발생 단계가 상세히 연구되었으며, 연소 불안정 발생 이후 압력 섭동의 진폭이 트리거링을 위해 입력된 소음의 세기와 유관함이 보여지기도 하였다[14].

이처럼 트리거링은 연소 시스템을 모사한 저차 수치 모델은 물론이고 리케 튜브[20]를 포함한 열음향 덕트형 연소기[14], 가스터빈 연소기[22]와 로켓 엔진의 연소실[23] 등 다양한 연소 시스템에서 광범위하게 관찰되는 소음 기반 동역학적 현상으로, 준임계 호프 분기 전후의 연소 시스템 설계 및 운용 과정에서 반드시 고려되어야 하는 요소이다.

2.2 소음 유도 간헐성 및 플리커링

간헐성(intermittency)은 동적 시스템이 주기적 진동 등의 정규적(regular) 상태와 카오스 등의 비정규적(irregular) 상태를 반복적으로 겪는 현상을 의미한다[24]. 이는 두 개의 서로 다른 끌개 영역(basin of attraction) 인근에서 시스템이 빠르게 두 상태를 오가는 플리커링(flickering) 현상[25]의 일종으로, 하나의 상태에서 다른 상태로의 전환이 소음의 입력에 의해 쉽게 일어나는 상황에서 관찰된다[26].

비선형동역학적 연구에 따르면 연소 소음(combustion noise)은 단순한 잡음이 아니라 카오스 상태이며[27], 따라서 연소 소음에서 열음향 자려진동으로 발달하는 연소 불안정의 발생은 카오스에서 한계 순환으로의 상태 전환으로 인식되고 있다. 이러한 사실로 인하여 카오스 끌개와 한계 순환 끌개가 동시에 존재하는 연소 불안정 발생 지점 부근에서 간헐성이 관찰되고 있는데, 이는 레이놀즈수와 평형비, 화염 밀도비 등 다양한 변수의 변화로 인해 발생하는 연소 불안정 현상에서 일관적으로 보고되었다[28,29,30].

간헐성은 끌개 사이에서 소음이 유도하는 상태 전환[31]에 의해 발생하며, 입력되는 소음 에너지에 따라 간헐성의 발생이 촉진될 수 있음이 수치 연구에 기반해 보여졌다[32,33]. 그러므로 플리커링의 한 형태인 간헐성의 발생은 연소 시스템에서 관찰되는 소음 기반 동역학적 거동의 한 형태로서 받아들여지고 있다. 또한, 간헐성은 연소 불안정이 발생하는 호프 분기[28]와 희박 가연 한계(lean blowout limit) 부근[34]에서 빈번히 발생하므로, 하술할 연소 시스템의 진단 문제에도 현상학적으로 활용할 수 있음이 주장된 바 있다[28,29,30].

3. NID 활용 연소 시스템 진단

3.1 감쇠 인자 및 임계 감속 기반 진단

연속 연소 시스템의 진단은 연소실의 주요한 동적 변화를 예측하고 회피하고자 하는 목적에서 이루어져 왔으며, 이러한 진단은 주로 로켓 연소실과 같이 연소 불안정에 취약한 시스템의 설계 및 운용 단계에서 연소 불안정에 이르기까지의 안정성 여유(stability margin)를 판단하는 방식으로 수행된다. 전통적인 기법에서는 선형 안정성 이론에 기반하여 유동의 열방출률 섭동과 압력 섭동 간의 위상 이동을 증폭 지수(n) 및 시간 지연(τ) 등으로 평가하는 방식의 수치적, 실험적 진단이 수행되었으며[35,36,37], 음향 모드 간의 비선형적 상호작용을 고려한 조화 진동자 기반의 해석도 활발히 연구되어왔다[38,39,40,41,42]. 후자의 연구에서는 연소실의 각 음향 모드에 화염의 열방출률 섭동 특성을 나타내는 항을 포함시킨 저차 진동자 모델을 사용, 해당 수식의 감쇠 인자(damping coefficient)로부터 안정성 여유를 판단하는 진단 방식이 사용되었다[41,42].

이러한 저차 모델에서의 감쇠 인자는 시스템의 교란을 소산시키는 모든 물리적 요소를 축약적으로 표현하는 값으로, Eq. 1과 Eq. 2에서의 -𝜖값과 같은 형태로 이해할 수 있다. 따라서, 감쇠 인자는 시스템의 안정 상태에서 양수이고 연소 불안정에 가까워질수록 단조 감소하며, 감쇠 인자가 0이 될 때 연소 불안정이 발생한다. 이러한 특성을 바탕으로, 연소 시스템을 펄스 인젝터나 음향 신호 등으로 가진하여 해당 외란이 소산되는 시간을 측정하는 방식으로 감쇠 인자 기반의 연소 불안정성 진단이 수행된 바 있다[41]. 그러나 이와 같은 방식은 인위적인 가진이 필요하므로, 연소 시스템 이외의 추가적인 설비가 필요할 뿐 아니라 연구실 수준의 연구장치를 벗어난 실질적인 대규모 연소 시스템에 적용이 어렵다는 한계가 존재하였다. 이러한 한계에 주목하여 외부 가진 없이 연소 과정에서 발생하는 자체적인 소음으로부터 유도되는 소음 기반 동역학적 특성으로부터 감쇠 인자를 추출하는 연구가 수행되었다[11]. 구체적으로, 해당 연구에서는 연소기 내부의 확률적 압력 섭동의 감쇠를 자기상관(autocorrelation)함수의 포락선 감쇠로부터 유도하여 연소기의 안정성 한계를 실험적으로 진단하였다. 이러한 연구는 하나의 관점에서 4장에서 기술할 소음 기반 동역학을 활용한 저차 모델링에서 파악하고자 하는 변수 중 하나인 선형 인자의 추산으로 받아들일 수 있으며, 다른 관점에서는 동적 시스템이 분기에 가까워질수록 외란에 반응하는 속도가 감소하는 임계 감속(critical slowing down)을 활용한 예시로도 볼 수 있다.

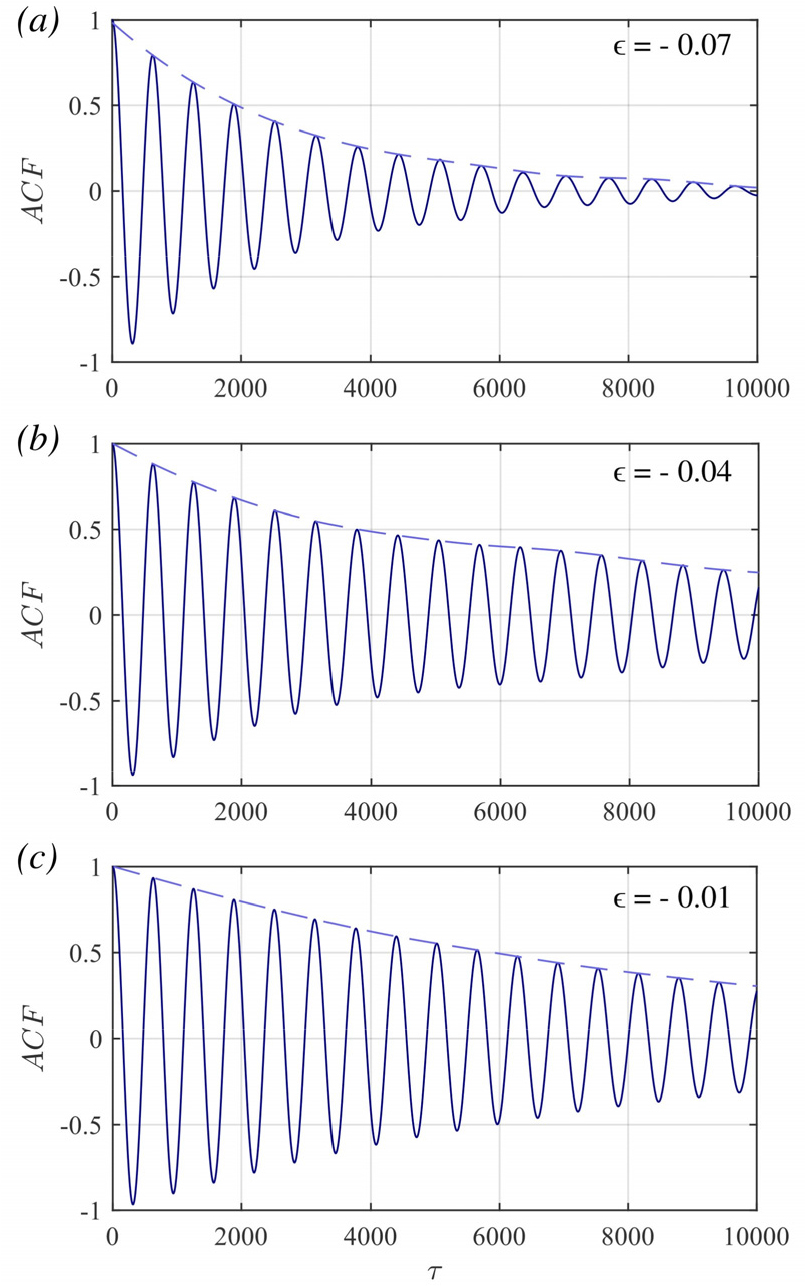
임계 감속은 끌개 영역의 전환이 발생하는 분기 인근에서 동적 시스템의 복원력(resilience) 감소로 인해 시스템이 원래의 상태로 복귀하는 시간이 감소하는 현상으로, 자기상관함수뿐 아니라 회복 시간과 분산 등 다양한 통계적 특성으로부터 파악된다[25,26,43,44]. 상술한 바와 같이 호프 분기로 해석할 수 있는 열음향 시스템에서도 임계 감속으로 드러나는 통계를 활용하여 시스템이 분기에 접근함을 진단할 수 있음이 수치적, 실험적으로 보여진 바 있다[44]. 해당 연구에서는 열음향 불안정으로 분기하는 준임계 호프 분기 인근의 리케 튜브 및 이를 모사한 수치모델에서 시스템이 분기에 가까워질수록 압력 섭동의 분산과 자기상관함수가 증가함을 확인하였는데, 이와 같은 변화는 실제 분기가 발생하기 이전부터 관찰되므로, 열음향 불안정성에 대한 진단을 수행할 수 있을 것으로 보았다. 즉, Fig. 4와 같이 저차 수치모델에서 감쇠 인자가 감소할수록 자기상관함수가 느리게 감소하는 것을 확인할 수 있으므로, 역으로 자기상관함수의 감소율을 이용하여 시스템의 감쇠 인자를 판단할 수 있는 것이다. 이처럼 시스템이 소음으로 인한 교란에서 원래의 동적 상태로 복귀하는 특성을 활용하여 연속 연소 시스템의 진단이 다양한 기법을 기반으로 수행되었으며, 이러한 진단은 인위적인 소음 가진이 없는 상태에서도 수행할 수 있어 범용성이 높은 것으로 평가된다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F4.jpg

Fig. 4.

Decay of the autocorrelation function (ACF) at various linear coefficients (𝜖). ACF decays slower as $| ϵ |$ approaches zero. Data used in these figures are obtained from the numerical simulation: $α_{1} = - 2, α_{2} = 0$ , and $d = 10^{- 4}$ (see Eq. 2). 𝜏 is the time delay in arbitrary unit used for the calculation of the ACF.

3.2 시계열 특성 변화 기반 진단

시계열 신호에 소음이 작용할 경우, 엔트로피와 프랙탈리티와 같은 비선형동역학적 특성이 변화한다[45,47]. 이러한 특성을 활용하여 압력과 열방출률 섭동이 상호 피드백을 일으키는 열음향 시스템에서 소음이 작용하는 시계열 신호의 특성 변화가 상태 진단에 활용되기도 하였다. 선행적 연구에서 Gotoda 등[45,46]은 가스터빈 연소기의 희박 예혼합 화염이 연소 불안정을 거쳐 희박 가연 한계에 이르기까지 압력 신호의 비선형적 변화를 분석하였다. 해당 연구에서는 비선형 시계열 해석을 통해 평형비의 증가에 따라 압력 섭동 신호가 소음이 지배하는 확률적 특성을 상실하고 저차원의 카오스 상태를 거쳐 주기성을 가지게 된다고 보고하였으며, 이러한 변화를 신호의 임의도(randomness)를 나타내는 퍼뮤테이션 엔트로피(permutation entropy)와 멀티프랙탈 차원(multi-fractal dimension) 등으로 수치화하여 연소기 진단에 활용할 수 있음을 제시하였다. 이후 Hachijo 등[48]의 후속 연구에서는 신호의 불균일도(disequilibrium)를 나타내는 젠슨-섀넌 복잡도(Jensen-Shannon complexity)와 퍼뮤테이션 엔트로피를 결합한 복잡도-엔트로피 인과 평면(complexity-entropy causality plane, Fig. 5) [49,50,51]을 활용하여 시계열의 임의도 상실과 불균일도 증감을 관찰하였다. 또한, 압력 신호 이외에 연소기의 열방출률 신호를 동시에 고려한 임의도-복잡도 해석이 수행되기도 하였다[51]. 평형비와 같은 분기 변수 변화에 따른 압력 및 열방출률 섭동 신호의 비선형적 변화가 온전히 소음 기반 동역학적인 작용에 의한 것은 아니나, 신호에 작용하는 소음의 효과를 계량함으로써 연소 시스템의 상태를 진단할 수 있다는 의미에서 상기한 연구의 의미를 평가할 수 있다.

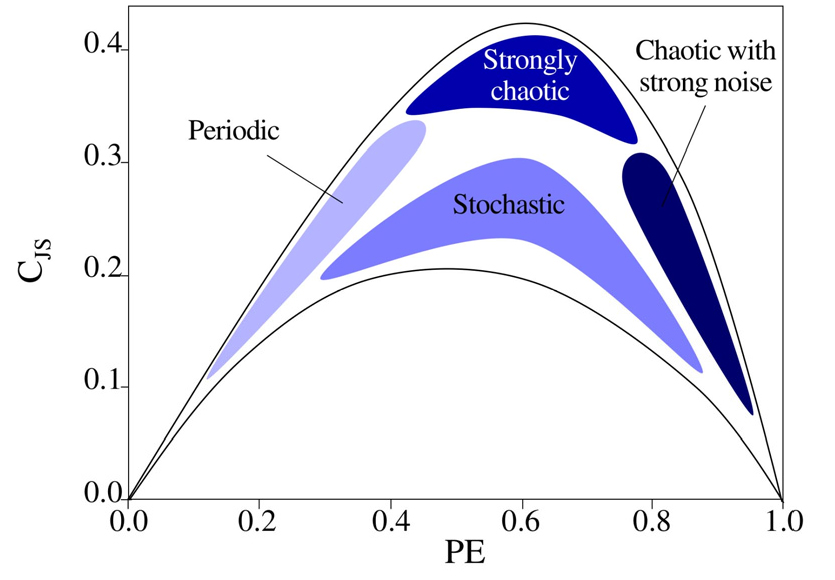
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F5.jpg

Fig. 5.

A rough illustration of the complexity-entropy causality plane depicting different categories of the dynamical states[51].

이와 더불어 2장에서 기술한 간헐성 등 소음 기반 동역학의 현상학적 특성을 활용한 연소 시스템의 진단도 수행되었다. Nair 등[28,34]은 실험실 규모의 난류 연소기에서 시스템이 열음향 불안정과 희박 가연 한계에 가까울수록 간헐성의 발생이 잦으며 시계열 중 고진폭 부분의 진동이 더욱 오래 지속됨을 관찰하였으며, 이를 통해 간헐성 경로로의 연소 불안정 발생 가능성을 진단할 수 있음을 주장하였다. 또한, Aoki 등[52]은 모델 로켓 연소기의 음향 모드에 의해 발생하는 간헐적인 압력 서지 현상을 퍼뮤테이션 스펙트럼 평가, 복잡도-엔트로피 곡선 평가 및 그래프 네트워크 기법 등을 통해 분석하여 그 특성을 정량화하고, 이러한 기법을 통해 연소실의 섭동을 진단할 수 있음을 제시하였다. 유사한 맥락에서, 시계열 패턴 형성과 같이 소음이 유발하는 현상학적 특성을 정량화하여 연소실의 동특성을 진단하고 변화를 예측할 수 있음이 알려진 바 있다[53].

4. NID 기반 연소 시스템 모델링

4.1 확률적 공진 및 코히어런스 공진

본 장에서는 소음 기반 동역학을 활용하여 연소 시스템의 저차 모델을 구성한 연구에 대해 짚어보도록 한다. 이를 위해서는 우선 소음이 시스템에 작용할 때 무소음 상태보다 명확한 모델링을 수행할 수 있게 하는 요인에 대한 분석이 필요하다. 소음의 작용은 때때로 신호의 명확성을 증진시키는 역할을 하는데, 이와 관련된 대표적인 현상으로 확률적 공진(stochastic resonance)이 있다. 확률적 공진이란, 주기성(periodicity)을 가진 미약한 신호가 동적 시스템에 작용하고 있을 때, 해당 신호가 소음의 입력으로 의해 증폭되는 현상을 일컫는다[54]. 이와 같은 현상은 시스템에 작용하는 주기적 신호의 신호대 잡음비(signal-to-noise ratio)를 증가시켜 관측을 용이하게 하므로, 자연적이거나 인위적으로 발생하는 소음의 효과를 이용하여 광학부터 지구과학에 이르기까지 다양한 물리적 시스템의 진단 및 모델링에 사용되어왔다[54,55].

확률적 공진이 시스템에 작용하는 외부의 주기적 신호가 소음에 의해 증폭되는 현상을 나타낸다면, 이와 유사한 현상인 코히어런스 공진(coherence resonance)은 시스템의 자체적인 신호가 소음에 의해 증폭되는 현상을 일컫는다[56]. 코히어런스 공진은 소음이 신호대 잡음비를 높인다는 측면에서 확률적 공진의 한 갈래로서 이해되기도 하는데, 이로 인해 초기 연구에서 코히어런스 공진은 주기적 신호가 배제된 확률적 공진 혹은 자동(autonomous) 확률적 공진으로 일컬어지기도 하였다[56,57,58,59]. 시스템에 작용하는 소음이 지나치게 강하면 무작위적 특성이 신호의 동특성을 지배하고, 지나치게 약하면 공진이 발생하지 않으므로, 소음 세기의 증가에 따라 코히어런스 공진 현상이 점차 뚜렷해지다가 다시 미약해지며, 중간 세기의 소음에서 공진이 최대가 된다고 알려졌다[60]. 코히어런스 공진은 2장에서 언급된 트리거링과 같이 호프 분기 이전의 시스템에서 뚜렷하게 관찰되므로, 호프 분기로 대표되는 연소 불안정 현상의 전구적 현상으로서 효과적으로 활용될 수 있다. 실제로, Kabiraj 등[61]은 준임계 호프 분기를 통해 연소 불안정 상태로 분기하는 열음향 시스템에서, 분기 이전의 연소기에서도 약한 주기성의 압력 섭동이 관찰됨을 확인하였다. 이러한 상태의 연소기에 적절한 세기의 소음이 입력되는 경우 압력 섭동의 진폭이 커지며 시스템 자체 신호가 공진하는 코히어런스 공진 현상이 관찰되었다. 또한, 압력 섭동 데이터로부터 계산된 자기상관 함수의 감쇠 추이로부터 이와 같은 코히어런스 공진 현상은 중간 세기의 소음에서 최대가 되는 것이 확인되었다. 이렇게 중간 세기의 소음에서 코히어런스 공진으로 인해 신호의 주기성이 최대가 되는 현상은 Fig. 6 및 Fig. 7과 같이 저차 수치 모델에서도 확인할 수 있다. 나아가, 코히어런스 공진은 수치모델을 포함한 다양한 연소 시스템에서 관찰되어 연소 불안정성의 예측 뿐 아니라 모델링에도 활용할 수 있음이 제시된 바 있는데[62], 이는 공진 발생 시 시스템 변수의 변화 없이도 압력 섭동 등의 시스템 진동 특성이 명확해져 섭동 모델 등 저차 모델의 인자를 추출하기 용이해지기 때문이다. 이러한 관점에서, 다음 절에 하술할 바와 같이 의도적으로 연소 시스템에 소음을 입력하여 코히어런스 공진을 유도하고, 이때 계측된 데이터를 바탕으로 연소 시스템의 저차 모델링을 수행하는 기법이 연구되었다[17].

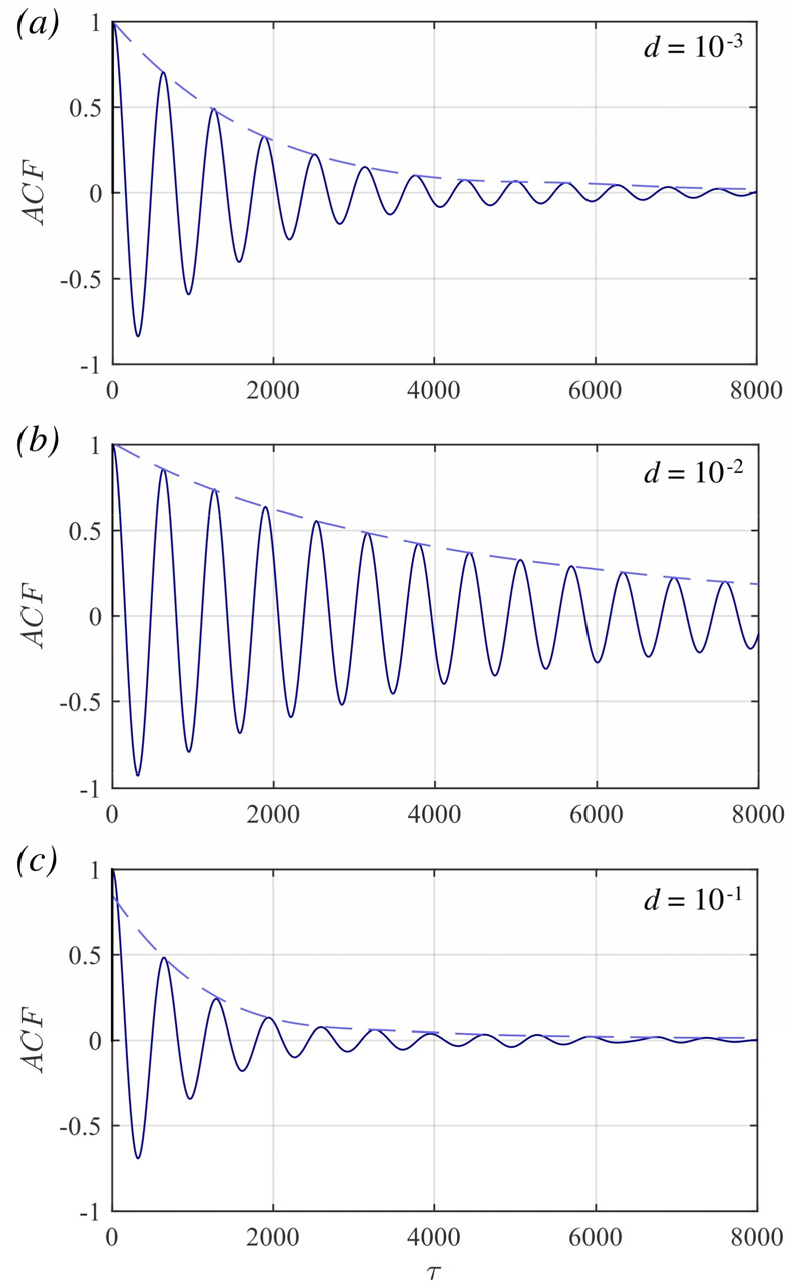
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F6.jpg

Fig. 6.

Figures illustrating the nonmonotonic behavior of autocorrelation function (ACF) decay under the influence of coherence resonance. The coherence of the signal reaches the maximum at the intermediate noise level. Dashed lines indicate the envelope of ACF, and 𝜏 is the time delay in arbitrary unit used for the calculation of the ACF. Data used in these figures are obtained from the numerical simulation: $ϵ = - 0.13, α_{1} = 2$ , and $α_{2} = - 4$ (see Eq. 2).

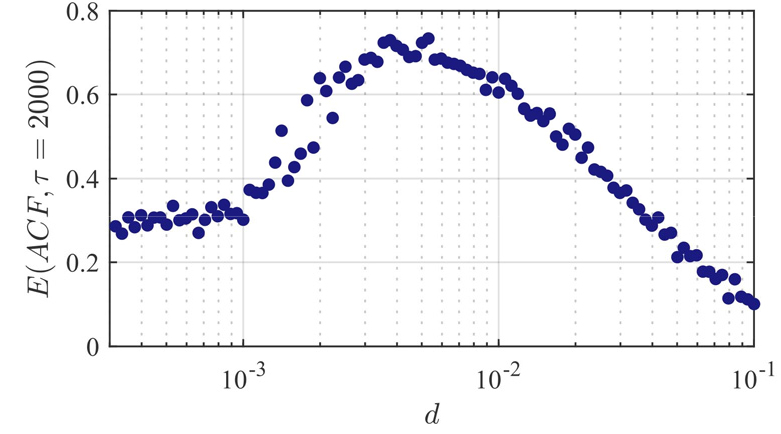
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F7.jpg

Fig. 7.

Change in the autocorrelation function (ACF) decay upon varying noise amplitude $d$ . Y-axis is the envelope of the ACF (dashed lines in Fig. 6) at 𝜏=2000 (in arbitrary unit). ACF decay is the slowest in the intermediate noise amplitude ( $d \approx 5 \times 10^{- 3}$ ). Linear and nonlinear coefficients are kept identical to Fig. 6. Note the logarithmic scale of the X-axis.

4.2 NID 기반 시스템 식별 기법

연속 연소 시스템의 소음 기반 동역학적 특성은 시스템의 동특성을 나타내는 저차 모델을 구성하고, 해당 모델의 변수를 추출하는데 사용된 바 있다. 이는 3장에서 기술한 것과 같은 일부 변수에 대한 식별부터, 시스템 모델의 전체 변수를 파악하는 역문제(inverse problem) 기반 기법까지 다양하게 시도되었다. 시스템에 작용하는 소음의 효과를 반영하는 방식의 모델링은 대부분의 경우 소음의 확률적 효과를 모사하기 위해 Eq. 2와 같이 확률 미분방정식 형태의 랑주뱅(Langevin) 방정식을 활용하게 된다. 랑주뱅 방정식은 압력 섭동 등 시스템 변수의 결정론적 거동을 지배하는 항과 소음의 영향을 표현하는 확률 항의 합성으로 구성되며, 입자와 같은 시스템의 미소한 구성 요소의 거동을 나타낸다. 전체 시스템 측면에서 이러한 미소 요소들의 집합적 거동을 고려할 경우, 개별 요소의 확률적 거동을 기반으로 계 전체의 거동에 대한 확률 분포를 모사할 수 있는데, 이는 포커-플랑크 방정식(Fokker-Planck equation)으로 표현된다[63]. 임의의 시스템 변수 x에 대한 포커-플랑크 방정식은 아래와 같다:

(3)

\frac{\partial}{\partial t} P (x, t) = - \frac{\partial}{\partial x} [D^{(1)} (x) P (x, t)] + \frac{\partial^{2}}{\partial x^{2}} [D^{(2)} (x) P (x, t)] .

여기서 $P (x, t)$ 는 변수 x의 시간(t)에 따른 확률 분포이며, $D^{(1)}$ 은 x의 결정론적 거동을 묘사하는 드리프트(drift) 항, $D^{(2)}$ 는 확률적 요소를 나타내는 확산(diffusion) 항이다. 좌변이 0이 되는 정상 상태 확률 분포에 대해 간소화된 포커-플랑크 방정식 형태를 제외하면 일반적으로 위 방정식의 일반해는 해석적으로 구하기 어렵다[64]. 따라서 대부분의 경우 포커-플랑크 방정식을 활용한 해석과, 이 방정식의 역문제를 통해 시스템 모델의 변수를 추출하는 과정은 수치적인 방법에 의존하고 있다[16,64,65,66].

Noiray 등[16]은 포커-플랑크 방정식을 연소 시스템의 모델링에 직접적으로 활용할 수 있음을 보였다. 해당 연구자들은 신호 섭동 진폭의 확률밀도함수를 활용하여 포커-플랑크 방정식의 드리프트 항과 확산 항을 식별할 수 있음을 제시한 Siegert 등[67]의 연구를 응용하여, 가스터빈 연소기 내 압력 섭동에 대한 모델링을 수행하였다. 저차 모델로서 한계 순환에 대한 반 데르 폴 진동자 형태(Eq. 2)에 소음 항을 결합하여 활용하였으며, 해당 식의 선형 및 비선형 변수를 포커-플랑크 방정식의 드리프트 항과 확산 항으로부터 추출하였다. 이러한 시스템 식별 연구는 외부의 인위적인 소음 입력을 배제하고 연소기 내의 자연적인 소음에 의해 가진된 압력 신호만을 활용하여 수행되었으며, 후속 연구[68]에서는 해당 방법론을 활용하여 열음향 시스템에 대한 모델 기반 피드백 제어 기법이 제시되기도 하였다. 이와 같이 진동자 모델을 사용한 연소 시스템의 저차 모델링은 단 하나의 섭동 모드만이 시스템에 존재함을 가정하므로, 해당 모드 부근의 밴드패스 필터링 등 전처리가 필요하다. 그러나 이러한 전처리는 소음의 무작위성, 즉 마르코프 성질(Markovian property)을 파괴하므로, 소음 기반 동역학적 특성이 시스템 식별에 온전히 반영되지 못한다는 단점이 존재하였다. 이러한 문제는 수반(adjoint) 미분방정식 형태의 포커-플랑크 방정식을 활용한 최적화를 수행하여 일부 해결할 수 있으나[64,65], 여러 개의 섭동 모드가 존재하는 등 복잡한 동특성을 지닌 연소 시스템을 단순한 진동 모델로써 모사하는 경우 모델의 정확성이 필연적으로 희생된다.

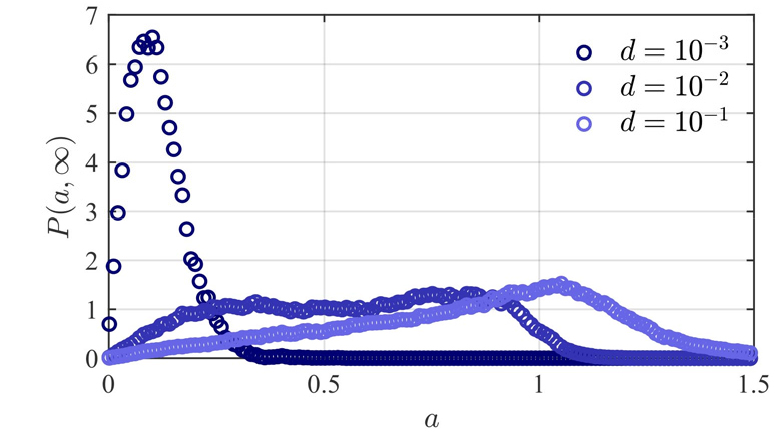
연소기 내부에서 자연적으로 발생하는 소음의 특성을 활용한 상기 모델링 기법과 달리, 인위적인 소음 입력을 통해 소음 기반 동역학적 특성을 유발시켜 연소 시스템의 모델링을 수행하는 입력(input)-출력(output) 방식의 시스템 식별 연구 또한 수행되었다. 이러한 입력-출력 방식의 연소 시스템 모델링은 소음의 세기(Eq. 2의 d)에 대한 정보를 보유한 상태에서 수행되므로, 실험적으로 계측된 섭동 진폭의 정상 상태 확률밀도함수(Fig. 8)만을 이용하여 시스템 변수를 추출할 수 있다는 장점을 가진다. 예를 들어, Lee 등[17]은 화염의 위치에 따라 초임계 호프 분기를 통해 열음향 불안정성으로 진행하는 리케 튜브를 백색 소음으로 가진하여 코히어런스 공진을 유도하였으며, 분기 이전의 시스템 변수를 식별하였다. 구체적으로, Ushakov 등[69]이 제시한 코히어런스 지수를 기반으로 소음 세기를 정량화하고, 입력되는 소음의 세기에 따른 압력 신호의 확률적인 반응을 정상 상태 포커-플랑크 방정식에 대입하여 선형 및 비선형 변수를 추출하였다. 나아가, 이를 통해 열음향 불안정성 발생 이전의 시스템 모델을 바탕으로 불안정성 발생 이후의 동특성을 예측할 수 있음이 제시되었다. 이와 같이 소음 기반 동역학적 모델링을 바탕으로 한 연소 불안정 예측 방식은 피스톤에 의해 연소실 길이가 변화하는 가스터빈 연소기[70]에서도 실험적으로 검증된 바 있다[71]. 이처럼 소음 기반 동역학을 활용한 연속 연소 시스템의 모델링 및 시스템 식별 기법은 시스템의 선형적, 비선형적 특성을 추출하여 안정 한계를 식별할 수 있게 할 뿐 아니라, 불안정성 발생 이후의 동특성까지도 예측할 수 있으며 연소기 제어에도 활용될 수 있으므로 단순한 시계열 진단 기법에 비해 높은 실용성을 가지는 것으로 평가된다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280206/images/ksssf_28_02_06_F8.jpg

Fig. 8.

Sample stationary probability density functions ( $P (a, \infty)$ of the oscillation amplitude ( $a$ , in arbitrary unit) at different noise levels. Data used in this figure are obtained from the numerical simulation: $ϵ = - 0.13, α_{1} = 2$ , and $α_{2} = - 4$ (see Eq. 2).

5. 결 론

본 논문에서는 연속 연소 시스템에 소음이 가해지는 경우 발생하는 현상을 고찰하고, 이와 같은 소음 기반 동역학적 특성을 기반으로 연소기의 진단 및 모델링을 수행한 연구 사례에 대해 기술하였다. 이를 통해 전통적인 결정론적 인식으로는 분석과 진단이 어려운 연소 시스템에 대한 다양한 연구 사례를 확인하였다. 본 논문에서 소개된 연구 이외에도 소음의 색상이나 신호 결합 형태와 같은 소음 특성에 따라 변화하는 연소 시스템의 소음 기반 동역학적 특성에 대한 연구가 현재 광범위하게 수행 중에 있으며, 이러한 연구를 통해 연속 연소 시스템의 동적 특성에 대한 이해를 증진시킬 수 있을 것으로 기대된다.

기 호 설 명

x : System parameter

a : Oscillation amplitude

ε : Linear coefficient

α_n : Nonlinear coefficient

d : Noise amplitude

ACF : Autocorrelation function

τ : Time delay

PE : Permutation entropy

C_JS : Jensen-Shannon complexity

P(x,t) : Probability density function

D⁽¹⁾ : Drift term

D⁽²⁾ : Diffusion term

References

P.K. Ezhil Kumar, D.P. Mishra, Combustion noise characteristics of an experimental 2D trapped vortex combustor, Aerosp. Sci. Technol. 43 (2015) 388-394. 10.1016/j.ast.2015.03.014

W.C. Strahle, Combustion noise, Prog. Energy Combust. Sci. 4(3) (1978) 157-176. 10.1016/0360-1285(78)90002-3

C.L. Morfey, Amplification of aerodynamic noise by convected flow inhomogeneities, J. Sound Vib. 31(4) (1973) 391-397. 10.1016/S0022-460X(73)80255-X

F.E.C. Culick, Combustion instabilities in liquid-fuelled propulsion systems, in: AGARD Conference Proceedings 430 (1988) 1-73.

L. Kabiraj, N. Vishnoi, A. Saurabh, A review on noise-induced dynamics of thermoacoustic systems, in: Dynamics and Control of Energy Systems, Springer (2020) 265-281. 10.1007/978-981-15-0536-2_12

F. Richecoeur, L. Hakim, A. Renaud, L. Zimmer, Dmd algorithms for experimental data processing in combustion, in: Proceedings of the Summer Program, Center for Turbulence Research (2012) 459-468.

I. Duran, S. Moreau, F. Nicoud, T. Livebardon, E. Bouty, T. Poinsot, Combustion noise in modern aero-engines, Aerospace Lab 7 (2014) 1-11.

M. Lee, J. Park, An optimized dynamic mode decomposition model robust to multiplicative noise, SIAM J. Appl. Dyn. Syst. 22(1) (2023) 235-268. 10.1137/21M1443832

W.W. Horsthemke, Noise-induced transitions: theory and applications in physics, chemistry, and biology., Springer-Verlag, 1984. 10.1007/978-3-642-46508-6_11

L.S. Tsimring, A. Pikovsky, Noise-induced dynamics in bistable systems with delay, Phys. Rev. Lett. 87(25) (2001) 250602. 10.1103/PhysRevLett.87.25060211736552

T.C. Lieuwen, V. Yang, Combustion instabilities in gas turbine engines: operational experience, fundamental mechanisms, and modeling, American Institute of Aeronautics and Astronautics, 2005. 10.2514/4.866807

M. Lee, System identification near a Hopf bifurcation via the noise-induced dynamics in the fixed-point regime, Ph.D. thesis, The Hong Kong University of Science and Technology (2020).

V.S. Burnley, F.E.C. Culick, Influence of random excitations on acoustic instabilities in combustion chambers, AIAA J. 38(8) (2000) 1403-1410. 10.2514/2.1116

V. Jegadeesan, R. Sujith, Experimental investigation of noise induced triggering in thermoacoustic systems, Proc. Combust. Inst. 34(2) (2013) 3175-3183. 10.1016/j.proci.2012.05.003

I.C. Waugh, M.P. Juniper, Triggering in a thermoacoustic system with stochastic noise, Int. J. Spray Combust. Dyn. 3 (3) (2011) 225-241. 10.1260/1756-8277.3.3.225

N. Noiray, B. Schuermans, Deterministic quantities characterizing noise-driven Hopf bifurcations in gas turbine combustors, Int. J. Non-Linear Mech. 50 (2013) 152-163. 10.1016/j.ijnonlinmec.2012.11.008

M. Lee, Y. Guan, V. Gupta, L.K.B. Li, Input-output system identification of a thermoacoustic oscillator near a Hopf bifurcation using only fixed-point data, Phys. Rev. E. 101(1) (2020) 013102. 10.1103/PhysRevE.101.01310232069669

K. Balasubramanian, R.I. Sujith, Thermoacoustic instability in a Rijke tube: Non-normality and nonlinearity, Phys. Fluids 20(4) (2008) 044103. 10.1063/1.2895634

S. Mariappan, R.I. Sujith, P.J. Schmid, Experimental investigation of non-normality of thermoacoustic interaction in an electrically heated Rijke tube, Int. J. Spray Combust. Dyn. 7(4) (2015) 315-352. 10.1260/1756-8277.7.4.315

M.P. Juniper, Triggering in the horizontal rijke tube: non-normality, transient growth and bypass transition, J. Fluid Mech. 667 (2011) 272-308. 10.1017/S0022112010004453

P.J. Schmid, Nonmodal stability theory, Annu. Rev. Fluid Mech. 39 (2007) 129-162. 10.1146/annurev.fluid.38.050304.092139

K.T. Kim, S. Hochgreb, Measurements of triggering and transient growth in a model lean-premixed gas turbine combustor, Combust. Flame 159(3) (2012) 1215-1227. 10.1016/j.combustflame.2011.10.016

Z. Wang, P. Liu, B. Jin, W. Ao, Nonlinear characteristics of the triggering combustion instabilities in solid rocket motors, Acta Astronaut. 176 (2020) 371-382. 10.1016/j.actaastro.2020.06.022

P. Bergé, Y. Pomeau, C. Vidal, Order within chaos, Wiley-VCH, 1987.

E.H. Van Nes, M. Scheffer, Slow recovery from perturbations as a generic indicator of a nearby catastrophic shift, Am. Nat. 169(6) (2007) 738-747. 10.1086/51684517479460

M. Scheffer, S.R. Carpenter, T.M. Lenton, J. Bascompte, W. Brock, V. Dakos, J. Van de Koppel, I.A. Van de Leemput, S.A. Levin, E.H. Van Nes, M. Pascual, J. Vandermeer, Anticipating critical transitions, Science 338(6105) (2012) 344-348. 10.1126/science.122524423087241

V. Nair, G. Thampi, S. Karuppusamy, S. Gopalan, R.I. Sujith, Loss of chaos in combustion noise as a precursor of impending combustion instability, Int. J. Spray Combust. Dyn. 5(4) (2013) 273-290. 10.1260/1756-8277.5.4.273

V. Nair, G. Thampi, R.I. Sujith, Intermittency route to thermoacoustic instability in turbulent combustors, J. Fluid Mech. 756 (2014) 470-487. 10.1017/jfm.2014.468

G. Thampi, R.I. Sujith, Intermittent burst oscillations: Signature prior to flame blowout in a turbulent swirl-stabilized combustor, J. Propul. Power 31 (6) (2015) 1661-1671. 10.2514/1.B35526

S. Suresha, R.I. Sujith, B. Emerson, T. Lieuwen, Nonlinear dynamics and intermittency in a turbulent reacting wake with density ratio as bifurcation parameter, Phys. Rev. E 94(4) (2016) 042206. 10.1103/PhysRevE.94.04220627841488

F.T. Arecchi, R. Badii, A. Politi, Generalized multistability and noise-induced jumps in a nonlinear dynamical system, Phys. Rev. A 32(1) (1985) 402. 10.1103/PhysRevA.32.4029896062

A.E. Hramov, A.A. Koronovskii, O.I. Moskalenko, M.O. Zhuravlev, R. Jaimes-Reategui, A.N. Pisarchik, Separation of coexisting dynamical regimes in multistate intermittency based on wavelet spectrum energies in an erbium-doped fiber laser, Phys. Rev. E 93(5) (2016) 052218. 10.1103/PhysRevE.93.05221827300891

O.I. Moskalenko, A.A. Koronovskii, M.O. Zhuravlev, A.E. Hramov, Characteristics of noise-induced intermittency, Chaos Solitons Fract. 117 (2018) 269-275. 10.1016/j.chaos.2018.11.001

V. Nair, R.I. Sujith, Intermittency as a transition state in combustor dynamics: An explanation for flame dynamics near lean blowout, Combustion Sci. Technol. 187(11) (2015) 1821-1835. 10.1080/00102202.2015.1066339

F.E.C. Culick, A review of calculations for unsteady burning of a solid propellant, AIAA Journal 6(12) (1968) 2241-2255. 10.2514/3.4980

K.-M. Kim, J.-K. Yoon, Linear stability analysis in a solid-propellant rocket motor, Trans. Korean Soc. Mech. Eng. 19(10) (1995) 2637-2646.

S.Y. Lee, Linear stability analysis of a baffled rocket combustor, J. of the Korean Society of Propulsion Engineers 22(3) (2018) 46-52. 10.6108/KSPE.2018.22.3.046

B.T. Zinn, E.A. Powell, Nonlinear combustion instability in liquid-propellant rocket engines, Symposium (international) on combustion 13(1) (1971) 491-503. 10.1016/S0082-0784(71)80051-6

F.E.C. Culick, Nonlinear behavior of acoustic waves in combustion chambers-I, Acta Astronaut. 3(9-10) (1976) 715-734. 10.1016/0094-5765(76)90107-7

F.E.C. Culick, Nonlinear behavior of acoustic waves in combustion chambers-II, Acta Astronaut. 3(9-10) (1976) 735-757. 10.1016/0094-5765(76)90108-9

C.E. Johnson, Y. Neumeier, T.C. Lieuwen, B.T. Zinn, Experimental determination of the stability margin of a combustor using exhaust flow and fuel injection rate modulations, Proc. Combust. Inst. 28(1) (2000) 757-763. 10.1016/S0082-0784(00)80278-7

T. Lieuwen, Online combustor stability margin assessment using dynamic pressure data, J. Eng. Gas Turbines Power 127(3) (2005) 478-482. 10.1115/1.1850493

L. Dai, D. Vorselen, K.S. Korolev, J. Gore, Generic indicators for loss of resilience before a tipping point leading to population collapse, Science 336(6085) (2012) 1175-1177. 10.1126/science.121980522654061

E.A. Gopalakrishnan, Y. Sharma, T. John, P.S. Dutta, R.I. Sujith, Early warning signals for critical transitions in a thermoacoustic system, Sci. Rep. 6(1) (2016) 1-10. 10.1038/srep3531027767065PMC5073343

H. Gotoda, H. Nikimoto, T. Miyano, S. Tachibana, Dynamic properties of combustion instability in a lean premixed gas-turbine combustor, Chaos 21(1) (2011) 013124. 10.1063/1.356357721456838

H. Gotoda, M. Amano, T. Miyano, T. Ikawa, K. Maki, S. Tachibana, Characterization of complexities in combustion instability in a lean premixed gas-turbine model combustor, Chaos 22(4) (2012) 043128. 10.1063/1.476658923278063

L. Ricci, A. Politi, Permutation entropy of weakly noise-affected signals, Entropy 24(1) (2021) 54. 10.3390/e2401005435052080PMC8774944

T. Hachijo, S. Masuda, T. Kurosaka, H. Gotoda, Early detection of thermoacoustic combustion oscillations using a methodology combining statistical complexity and machine learning, Chaos 29(10) (2019) 103123. 10.1063/1.512081531675849

L. Zunino, M. Zanin, B.M. Tabak, D.G. Pérez, O.A. Rosso, Complexity-entropy causality plane: A useful approach to quantify the stock market inefficiency, Physica A 389(9) (2010) 1891-1901. 10.1016/j.physa.2010.01.007

E. Han, D. Kim, J. Lee, Y. Kim, M. Yi, M. Lee, Analysis of the Hall-effect thruster discharge blowoff using complexity-entropy causality plane, J. Korean Soc. Aeronaut. Space Sci. 51(4) (2023) 263-271. 10.5139/JKSAS.2023.51.4.263

M. Lee, Early warning detection of thermoacoustic instability using three-dimensional complexity-entropy causality space, Exp. Therm. Fluid Sci. 130 (2022) 110517. 10.1016/j.expthermflusci.2021.110517

C. Aoki, H. Gotoda, S. Yoshida, S. Tachibana, Dynamic behavior of intermittent combustion oscillations in a model rocket engine combustor, J. Appl. Phys. 127(22) (2020) 224903. 10.1063/5.0001900

N.B. George, V.R. Unni, M. Raghunathan, R.I. Sujith, Pattern formation during transition from combustion noise to thermoacoustic instability via intermittency, J. Fluid Mech. 849 (2018) 615-644. 10.1017/jfm.2018.427

L. Gammaitoni, P. Hänggi, P. Jung, F. Marchesoni, Stochastic resonance, Rev. Mod. Phys. 70(1) (1998) 223. 10.1103/RevModPhys.70.223

B. McNamara, K. Wiesenfeld, R. Roy, Observation of stochastic resonance in a ring laser, Phys. Rev. Lett. 60(25) (1988) 2626. 10.1103/PhysRevLett.60.262610038407

H. Gang, T. Ditzinger, C.-Z. Ning, H. Haken, Stochastic resonance without external periodic force, Phys. Rev. Lett. 71(6) (1993) 807. 10.1103/PhysRevLett.71.80710055373

A. Longtin, Autonomous stochastic resonance in bursting neurons, Phys. Rev. E 55(1) (1997) 868. 10.1103/PhysRevE.55.868

M. Lee, Y. Zhu, L.K.B. Li, V. Gupta, System identification of a low-density jet via its noise-induced dynamics, J. Fluid Mech. 862 (2019) 200-215. 10.1017/jfm.2018.961

Y. Zhu, V. Gupta, L.K.B. Li, Coherence resonance in low-density jets, J. Fluid Mech. 881 (2019) R1. 10.1017/jfm.2019.782

A.S. Pikovsky, J. Kurths, Coherence resonance in a noise-driven excitable system, Phys. Rev. Lett. 78(5) (1997) 775. 10.1103/PhysRevLett.78.775

L. Kabiraj, R. Steinert, A. Saurabh, C.O. Paschereit, Coherence resonance in a thermoacoustic system, Phys. Rev. E 92(4) (2015) 042909. 10.1103/PhysRevE.92.04290926565306

V. Gupta, A. Saurabh, C.O. Paschereit, L. Kabiraj, Numerical results on noise-induced dynamics in the subthreshold regime for thermoacoustic systems, J. Sound Vib. 390 (2017) 55-66. 10.1016/j.jsv.2016.12.004

H. Risken, Fokker-Planck Equation, Springer, 1984. 10.1007/978-3-642-96807-5

M. Lee, K.T. Kim, J. Park, A numerically efficient output-only system-identification framework for stochastically forced self-sustained oscillators, Under Review.

E. Boujo, N. Noiray, Robust identification of harmonic oscillator parameters using the adjoint Fokker-Planck equation, Proc. R. Soc. A 473 (2200) (2017) 20160894. 10.1098/rspa.2016.089428484333PMC5415693

M. Lee, D. Kim, J. Lee, Y. Kim, M. Yi, A data-driven approach for analyzing hall thruster discharge instability leading to plasma blowoff, Acta Astronaut. 206 (2023) 1-8. 10.1016/j.actaastro.2023.02.017

S. Siegert, R. Friedrich, J. Peinke, Analysis of data sets of stochastic systems, Phys. Lett. A 243(5-6) (1998) 275-280. 10.1016/S0375-9601(98)00283-7

N. Noiray, A. Denisov, A method to identify thermoacoustic growth rates in combustion chambers from dynamic pressure time series, Proc. Combust. Inst. 36(3) (2017) 3843-3850. 10.1016/j.proci.2016.06.092

O.V. Ushakov, H.-J. Wünsche, F. Henneberger, I. A. Khovanov, L. Schimansky-Geier, M.A. Zaks, Coherence resonance near a Hopf bifurcation, Phys. Rev. Lett. 95(12) (2005) 123903. 10.1103/PhysRevLett.95.12390316197076

J. Lee, J. Park, D. Han, K.T. Kim, Subcritical bifurcation of two self-excited interacting swirl flames, J. Korean Soc. Combust. 24(2) (2019) 17-24. 10.15231/jksc.2019.24.2.017

M. Lee, K.T. Kim, V. Gupta, L.K.B. Li, System identification and early warning detection of thermoacoustic oscillations in a turbulent combustor using its noise-induced dynamics, Proc. Combust. Inst. 38(4) (2021) 6025-6033. 10.1016/j.proci.2020.06.057

Journal of the Korean Society of Combustion ISSN:1226-0959(Print) 2466-2089(Online) 한국연소학회지

Preview

Numerical Aspects of Noise-Induced Dynamics in Continuous Combustion Systems

ABSTRACT

MAIN

(1)

Fig. 1.

Illustration of (a) supercritical and (b) subcritical Hopf bifurcation. These figures are obtained by analytically solving Eq. 1 with varying 𝜖 and fixed αn: (a) α1=-2, α2=0, and (b) α1=2, α2=-4. Both x- and y-axis parameters are in arbitrary units.

(2)

Fig. 2.

Numerical examples of randomly triggered signals near a subcritical Hopf bifurcation. Data in these figures are obtained by numerically solving Eq. 2 with ϵ=-0.08, α1=2, α2=-4, and d=5×10-4. Both x- and y-axis parameters are in arbitrary units.

Fig. 3.

Fig. 4.

Fig. 5.

A rough illustration of the complexity-entropy causality plane depicting different categories of the dynamical states[51].

Fig. 6.

Fig. 7.

(3)

Fig. 8.

Sample stationary probability density functions (P(a,∞) of the oscillation amplitude (a, in arbitrary unit) at different noise levels. Data used in this figure are obtained from the numerical simulation: ϵ=-0.13,α1=2, and α2=-4 (see Eq. 2).

References

Illustration of (a) supercritical and (b) subcritical Hopf bifurcation. These figures are obtained by analytically solving Eq. 1 with varying 𝜖 and fixed $α_{n}$ : (a) $α_{1} = - 2$ , $α_{2} = 0$ , and (b) $α_{1} = 2$ , $α_{2} = - 4$ . Both x- and y-axis parameters are in arbitrary units.

Numerical examples of randomly triggered signals near a subcritical Hopf bifurcation. Data in these figures are obtained by numerically solving Eq. 2 with $ϵ = - 0.08$ , $α_{1} = 2$ , $α_{2} = - 4$ , and $d = 5 \times 10^{- 4}$ . Both x- and y-axis parameters are in arbitrary units.

Sample stationary probability density functions ( $P (a, \infty)$ of the oscillation amplitude ( $a$ , in arbitrary unit) at different noise levels. Data used in this figure are obtained from the numerical simulation: $ϵ = - 0.13, α_{1} = 2$ , and $α_{2} = - 4$ (see Eq. 2).