1. 서 론
2. 실험 장치 및 수치해석 방법
2.1 실험 장치 및 방법
2.2 EDMD 방법
3. 결과 및 고찰
3.1 수소 혼소율 변화의 효과
3.2 Pilot split ratio 변화의 효과
3.3 작동 압력 변화의 효과
3.4 조건별 경향 비교 및 FFT 적용
4. 결 론
1. 서 론
최근 발전용 가스터빈은 환경오염의 주 원인으로 꼽히는 오염 물질인 NOx의 저감, 음향 진동으로 발생하는 연소불안정 및 가스터빈의 성능 향상을 목표로 연구가 진행되고 있다. Koc 등[1]은 가스터빈의 성능을 분석하기 위해 재생 열교환기(recuperator)를 활용하여 50 MW급 가스터빈에서 수소와 천연가스를 각각 연료로 사용하였을 때의 열효율을 비교하여 수소를 연료로 사용할 경우, 가스터빈의 열효율이 향상됨을 확인하였다. Rodrigues 등[2]은 천연가스를 사용한 가스터빈 연소실의 길이를 조절하여 마하수와 체류 시간을 변화시켜, 마하수가 증가할수록, 체류 시간이 감소할수록 연소실 출구의 NOx가 줄어듦을 보였다. 연소불안정 유무를 판단하기 위해 Joo 등[3]은 예연소실과 연소실에서 얻은 속도와 열발생률 및 이들의 섭동으로 이득값과 위상차를 구하여 화염 전달 함수(flame transfer function, FTF)를 도출하였고, 고속 푸리에 변환(fast Fourier transform, FFT)을 사용하여 가스터빈에서 수소와 메탄의 비율에 따른 주파수와 성장률(growth rate)을 구하여 연소불안정을 분석하였다. Ruan 등[4]은 RP-3, RP-3/iso-octane, RP-3/n-dodecane을 연료로 사용하는 가스터빈에서 화염과 속도장의 진동 구조를 파악하기 위해 proper orthogonal decomposition(POD)을 사용하여 mode energy를 통해 화염의 속도장을 분석하였다.
최근 POD와 더불어 모드 해석이 가능한 exact dynamic mode decomposition(EDMD) 기법을 활용하여 여러 연구가 진행되고 있다. Rajasegar 등[5]은 예혼합 메탄-공기의 층류 화염, 스월 예혼합 버너의 OH-PLIF 이미지를 DMD 기법에 적용하여 주파수 별 성장률을 통해 DMD 기법이 연소불안정 분석에 사용될 수 있음을 보였다. Wang 등[6]은 수소와 메탄을 사용한 모형 가스터빈의 실험 결과에 FTF와 DMD 기법을 적용하였고 이를 FFT 결과와 비교하여 연소불안정이 일어날 수 있는 주파수의 범위를 나타내었다.
본 연구에서는 가스터빈 단일노즐에 대해서 화염의 광학측정이 가능한 시험리그에서 연소 시험을 진행하였으며 OH 자발광 및 동압 측정 데이터를 기반으로 혼소율, 연료 분배율(pilot split ratio) 및 작동 압력이 연소불안정에 미치는 영향을 파악하였다. 이를 위해 EDMD 기법을 적용하여 growth rate과 그에 상응하는 주파수를 도출하고, FFT 결과의 주파수 및 진폭과 실험으로 얻은 동압 결과를 비교하였다.
2. 실험 장치 및 수치해석 방법
2.1 실험 장치 및 방법
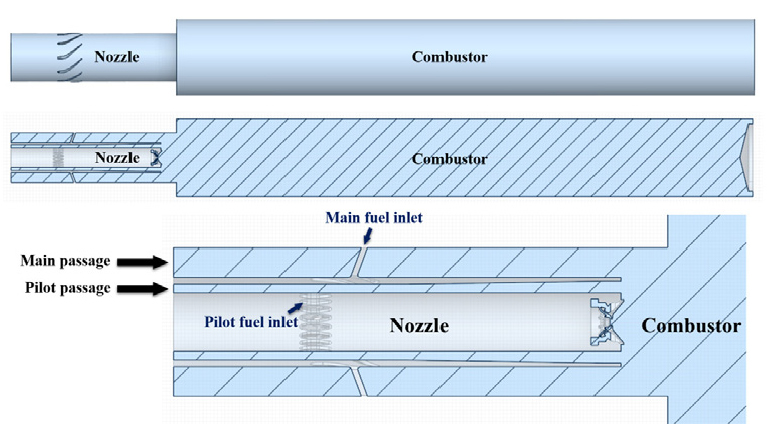
연소 시험은 대형 가스터빈에 적용되는 단일 노즐에 대하여 수행하였다. 해당 연소기 설비의 실험 조건에서 당량비는 혼소율에 따라 달라지며 pilot split ratio, 작동 압력과는 무관하다. 연소 시험을 수행한 성능 시험리그는 Fig. 1(a)에 나타난 바와 같이 전체 케이싱 안쪽에 노즐 장착부, 라이너 및 배기 배출부로 구성되어 있고, 라이너 상류에 OH 자발광 측정을 위한 가시화 쿼츠를 Fig. 1(b)와 같이 장착하였다. OH 자발광은 ICCD 카메라(Andor 社, iStar sCMOS)에 UV렌즈(Nikon 社, 105 mm UV f/4.5 Nikkor) 및 광학필터(300-320nm bandpass)를 장착하여 시험리그의 측면에서 측정하였다. Fig. 2(a)에 가시화 쿼츠창을 통한 OH 자발광 측정 예시가 나타나있고, Fig. 2(b)에는 EDMD 계산에 사용된 자발광 측정 영역이 나타나있다. 추가적으로, 연소불안정 특성 파악을 위해 노즐 출구 덤프면에 피에조일레트릭 타입의 동압센서(PCB 社, 106B)를 장착하여 동압을 측정하였다.
2.2 EDMD 방법
EDMD는 선형변환과 고유값, 고유 벡터를 통해 일정한 간격의 시간으로 추출한 데이터의 동적 특성을 분석하는 기법이다[7]. 먼저, 특정 시간에서 저장된 i 번째 snapshot을 vi로 나타내며 이들은 아래와 같은 matrix로 표현된다.
여기서 두 행렬은 n개의 위치에서 추출한 데이터를 포함하고 있으므로 (n, m)의 크기를 가진다. 본 연구에서는 혼소율과 작동 압력의 경우 1,000개의 snapshot을, pilot split ratio의 경우 500개의 snapshot을 사용하였다. 또한 snapshot 내에 586,746개의 위치에서 데이터가 저장되어 있다. 이들을 선형변환하면 아래와 같다.
여기서 A 행렬이 시스템의 동적 특성을 가지며 A 행렬의 고유값 및 고유 벡터는 mode shape, growth rate, 주파수와 연관이 있다. 연소불안정 관점에서, 성장률이 양수일 경우 압력 섭동 진폭은 시간에 따라 지수적으로 증가하고, 음수일 경우 진폭은 시간에 따라 감소함을 의미한다[8]. 따라서 growth rate을 정량적으로 구하기 위해 아래와 같이 특이값 분해(singular value decomposition, SVD)를 적용하였다.
위 식에서 U, W는 각각 (n,n), (m,m)의 크기를 가지며 VTV, VVT의 고유 벡터로 정의되는 직교 행렬이다. 따라서, 위의 과정과 UTAU가 A의 유사 행렬임을 활용하여 행렬 A의 고유값과 고유 벡터를 구하지 않고 식 (7)에서 좌변의 고유값과 고유 벡터를 통해 주파수와 growth rate를 구할 수 있다.
주파수와 growth rate은 아래와 같이 정량화된다.
여기서 fi는 i 번째의 주파수, Nstep은 time step의 개수, ∆t는 time step, p는 음향진동주기, ζi는 i 번째의 성장률, λi는 i 번째의 고유 벡터를 나타낸다. 따라서 자발광 측정 결과에 EDMD 기법을 적용하여 식 (8)-(9)로 주파수와 성장률을 구한 뒤, 연소불안정 여부를 판단하고 연소불안정이 발생할 경우 압력 섭동 주파수를 찾을 수 있다.
3. 결과 및 고찰
3.1 수소 혼소율 변화의 효과
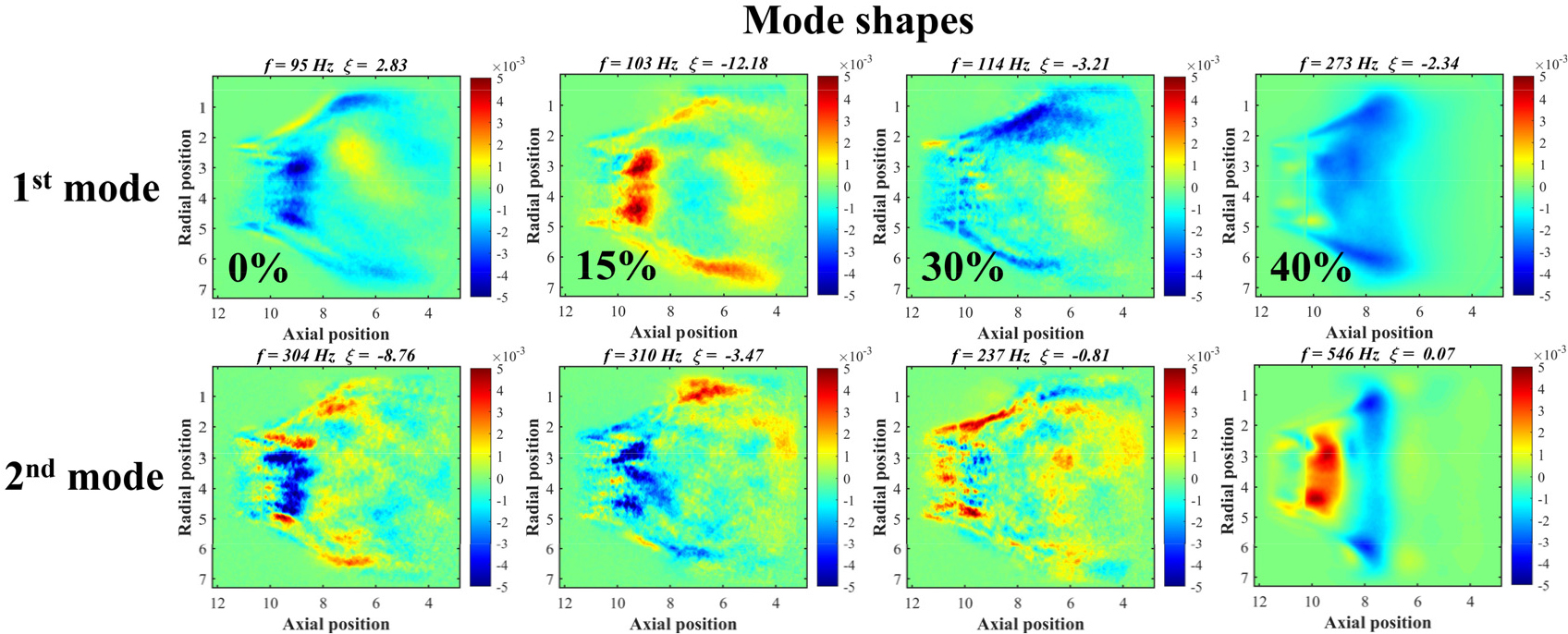
수소는, 가스터빈에 일반적으로 사용되는 메탄 연료와 달리 탄소 원자가 없어 오염 물질의 배출을 억제하기에 유용하지만 수소의 비율이 높아질수록 연소불안정이 발생할 가능성이 증가할 수도 있다. 따라서 pilot split ratio와 작동 압력을 각각 20%, 1.3 bar로 고정하고 혼소율을 변화시켜 연소불안정 발생 경향을 파악하였다. 이때 혼소율은 0%, 15%, 30%, 40%이며, 이에 해당하는 당량비는 각각 0.485, 0.481, 0.477, 0.473이다. 실험으로 얻은 자발광 snapshot을 EDMD 기법에 적용하여 계산된 종방향 mode shape을 Fig. 3에 나타내었고 모드별 주파수와 growth rate을 Tables 1, 2에 정리하였다.
Table 1.
Frequency and growth rate of the 1st longitudinal mode
| Hydrogen blending |
Frequency [Hz] | Growth rate [rad/s] |
| 0% | 93 | 2.83 |
| 15% | 103 | -12.18 |
| 30% | 114 | -3.21 |
| 40% | 273 | -2.34 |
Table 2.
Frequency and growth rate of the 2nd longitudinal mode
| Hydrogen blending |
Frequency [Hz] | Growth rate [rad/s] |
| 0% | 304 | -8.76 |
| 15% | 310 | -3.47 |
| 30% | 237 | -0.81 |
Fig. 3에서 보듯이, EDMD 기법으로 mode shape을 파악하였을 때 혼소율 40%에 비해 다른 조건에서는 종방향의 공진 모드가 명확하게 관찰되지 않았다. 또한 음향 공진이 발생한 경우, 2nd mode의 주파수는 1st mode의 주파수의 2배여야 하지만 혼소율 30%와 40%를 제외한 나머지 조건에서는 주파수 사이에 두배보다 큰 오차를 보였다. 수소 혼소율 0%의 경우, 1st mode의 진동은 양(+)의 성장률을 보였지만, mode shape으로부터 공진 현상이 야기되지 않았음을 알 수 있다. 이로부터, 혼소율 40%를 제외한 나머지 조건에서는, 실험에서 공진주파수가 측정되더라도 공진 현상이 발생하지 않았고 EDMD의 계산 결과로 나온 mode shape 또한 공진이 발생하지 않았음을 알 수 있다.
3.2 Pilot split ratio 변화의 효과
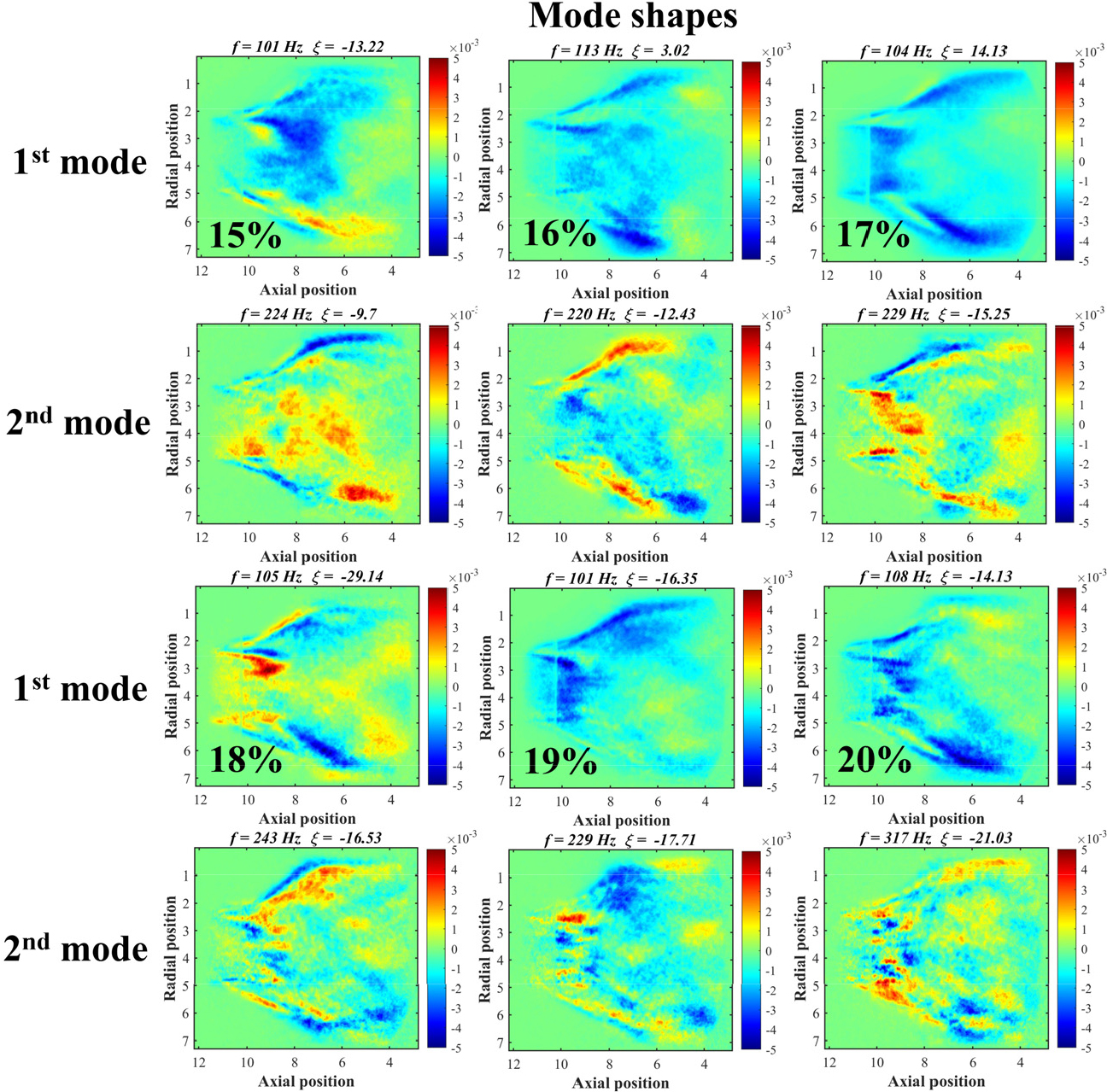
Pilot split ratio는, Fig. 4에 나타낸 노즐의 main passage와 pilot passage를 통해 연료가 공급될 때, pilot passage를 통해 공급되는 연료의 유량을 전체 연료 유량으로 나눈 값으로 정의된다. Pilot split ratio의 변화에 따른 연소불안정 발생 여부를 판단하기 위해 혼소율과 작동 압력을 각각 0%, 1.3 bar로 고정한 조건에서 pilot split ratio를 15%에서 20%까지 1%씩 변화시켜 EDMD 기법을 적용하였다. Fig. 5에 나타낸 종방향 mode shape으로부터, Fig. 3에서와 마찬가지로 공진된 모드를 관찰할 수 없다. Tables 3, 4에서 pilot split ratio, 20%를 제외한 나머지 조건에서 1st mode와 2nd mode의 주파수는 2배 관계에 있음을 확인하였다. 하지만 앞선 결과처럼 공진 모드의 mode shape이 나타나지 않았기 때문에 연소 실험중에 역시 공진이 발생하지 않았다고 판단된다.
Table 3.
Frequency and growth rate of the 1st mode
| Pilot split ratio |
Frequency [Hz] | Growth rate [rad/s] |
| 15% | 101 | -13.22 |
| 16% | 113 | 3.02 |
| 17% | 104 | 14.13 |
| 18% | 105 | -29.14 |
| 19% | 101 | -16.35 |
| 20% | 108 | -14.13 |
Table 4.
Frequency and growth rate of the 2nd mode
| Pilot split ratio |
Frequency [Hz] | Growth rate [rad/s] |
| 15% | 224 | -9.7 |
| 16% | 220 | -12.43 |
| 17% | 229 | -15.25 |
| 18% | 243 | -16.53 |
| 19% | 229 | -17.71 |
| 20% | 317 | -21.03 |
3.3 작동 압력 변화의 효과
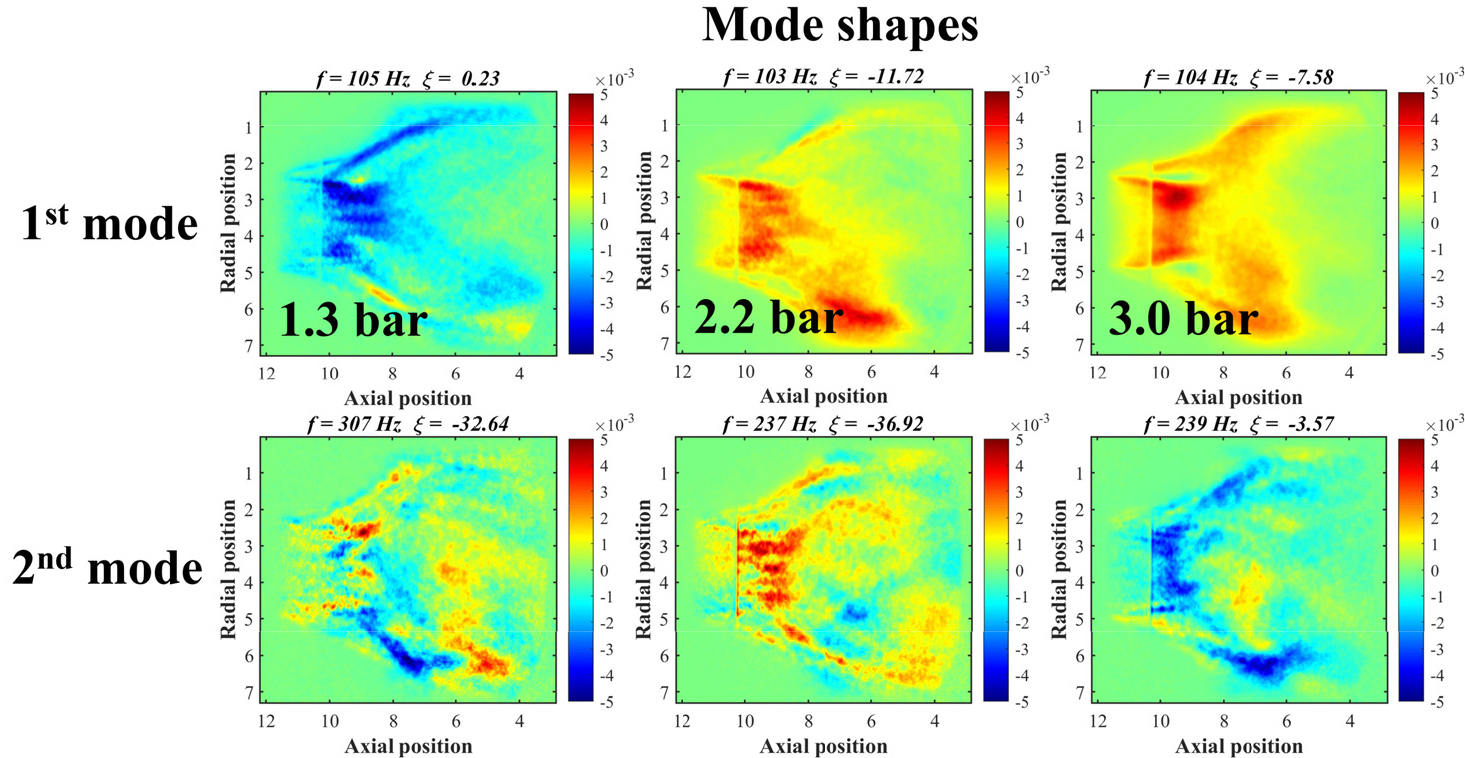
혼소율, pilot split ratio와 더불어 작동 압력이 연소불안정성에 미치는 영향을 알아보기 위해 혼소율과 pilot split ratio를 각각 0%, 20%로 고정한 조건에서 작동 압력을 1.3 bar, 2.2 bar, 3.0 bar로 변화시켜 얻은 결과를 EDMD 기법에 적용하였다. 해당 조건의 mode shape과 주파수, growth rate을 Fig. 6와 Tables 5, 6에 나타내었다. 앞선 결과와 마찬가지로 mode shape이 공진 현상을 뚜렷하게 보여주지 않으며, 1.3 bar에서 1st mode와 2nd mode 사이의 주파수 차이가 두배 이상 크게 나타났고 2.2 bar, 3.0 bar 조건에서는 약간의 오차가 있지만 2nd mode 주파수가 1st mode의 약 2배임을 알 수 있다. 결과적으로, 작동 압력 변화에 의해 음향 공진이 야기되지는 않는다고 판단할 수 있다.
Table 5.
Frequency and growth rate of the 1st mode
|
Pressure [bar] |
Frequency [Hz] | Growth rate [rad/s] |
| 1.3 | 105 | 0.23 |
| 2.2 | 103 | -11.72 |
| 3.0 | 104 | -7.58 |
Table 6.
Frequency and growth rate of the 2nd mode
|
Pressure [bar] |
Frequency [Hz] | Growth rate [rad/s] |
| 1.3 | 307 | -32.64 |
| 2.2 | 237 | -36.92 |
| 3.0 | 239 | -3.57 |
3.4 조건별 경향 비교 및 FFT 적용
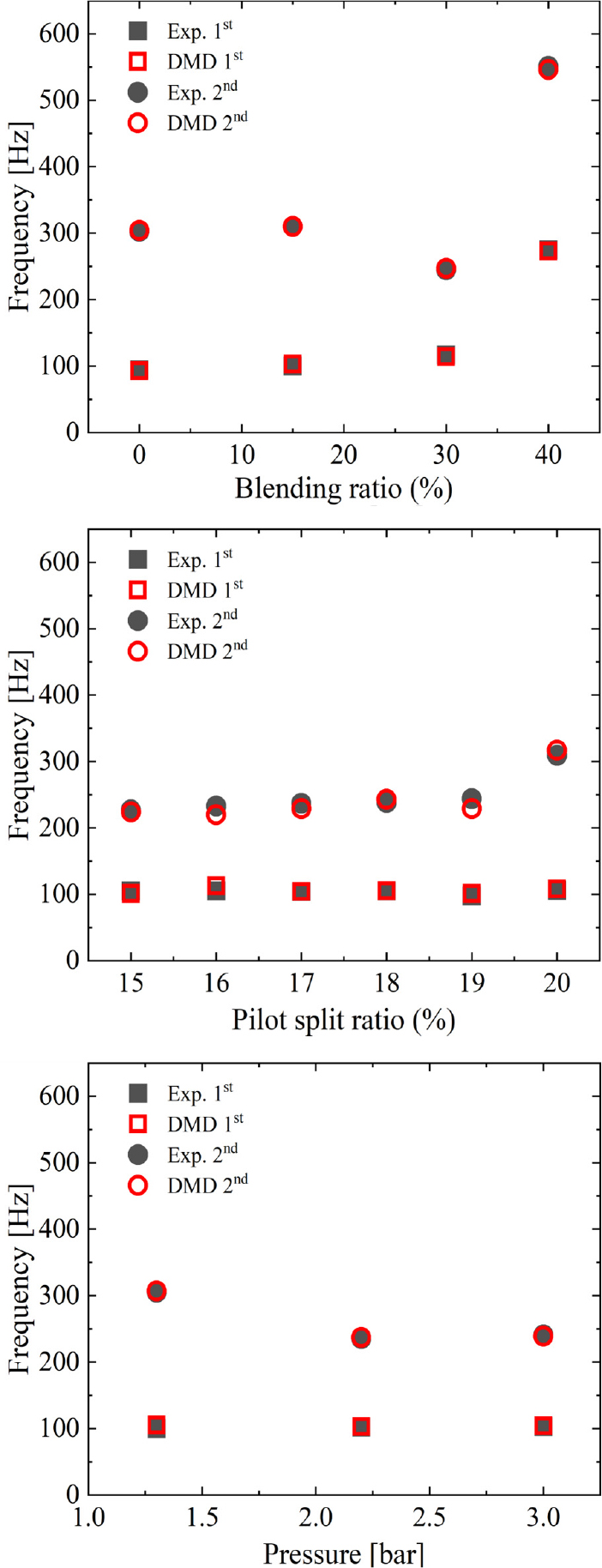
자발광 측정으로 구한 주파수와 EDMD 기법으로 계산한 주파수를 비교하여 Fig. 7에 나타내었다. 혼소율, pilot split ratio, 작동 압력 변화에 따라 수행한 실험과 EDMD 기법으로 구한 1st mode, 2nd mode의 주파수는 서로 근사하며 최대 오차는 각각 3%, 6%, 5%에 불과하였다. 이는, 자발광 측정 데이터를 사용한 EDMD 기법 적용으로 연소불안정을 야기할 수 있는 주파수를 정확하게 찾을 수 있음을 암시한다.
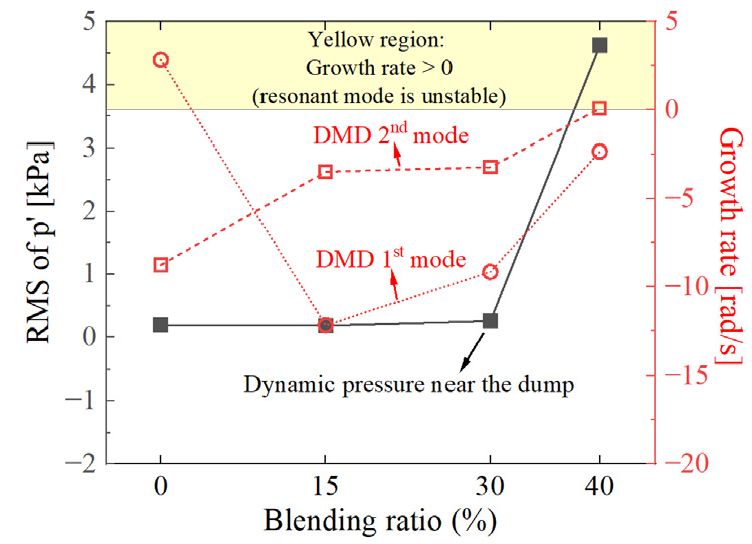
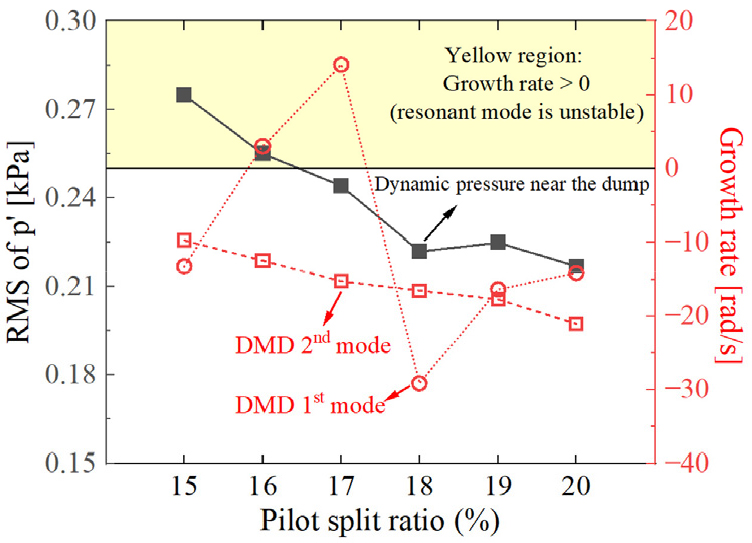
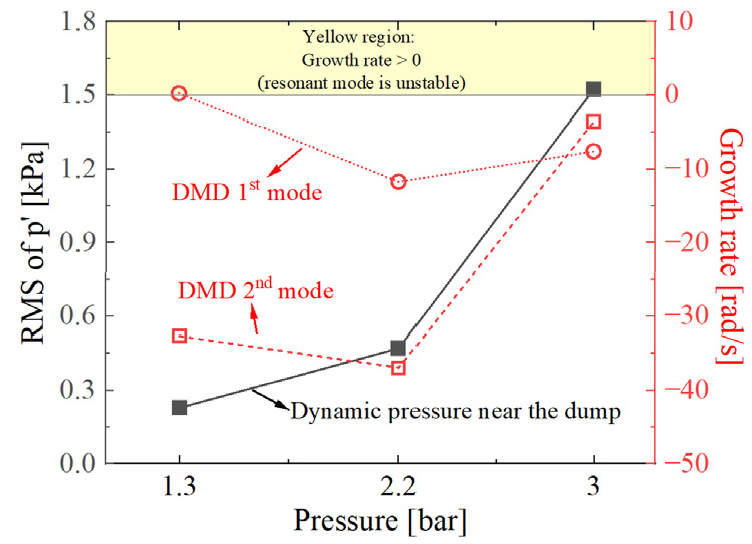
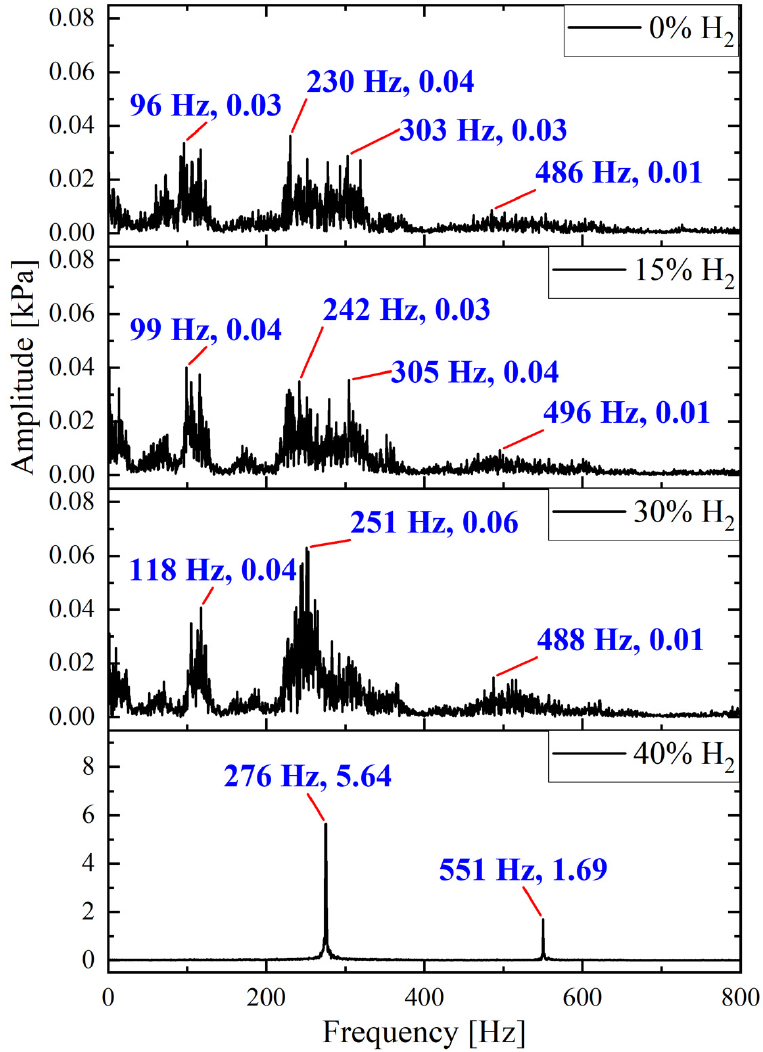
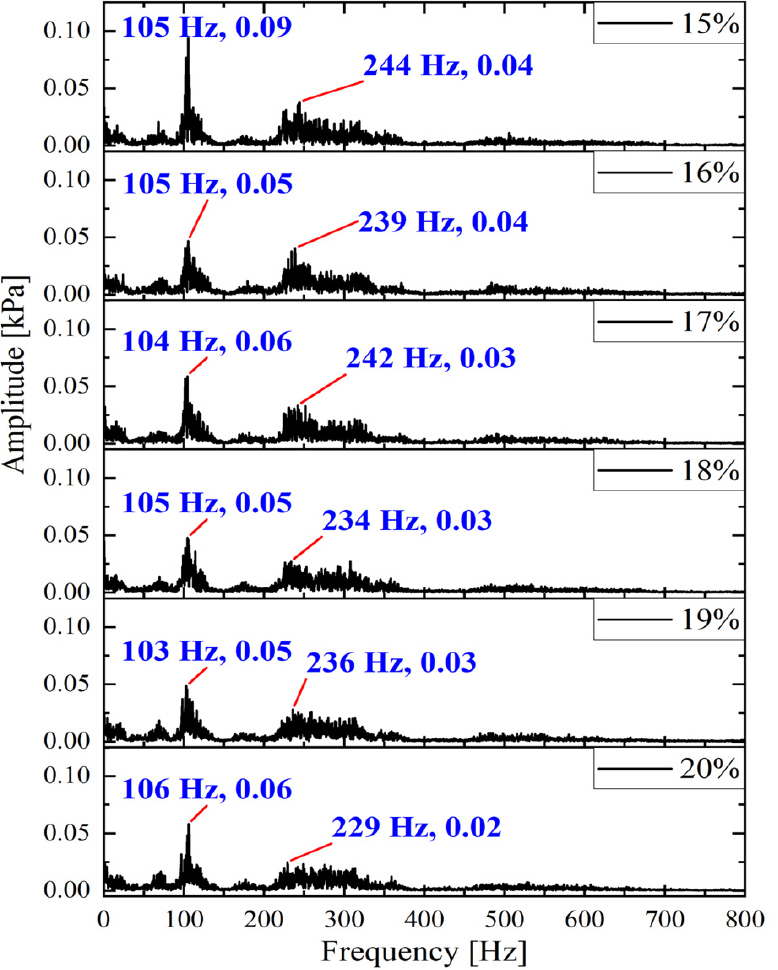
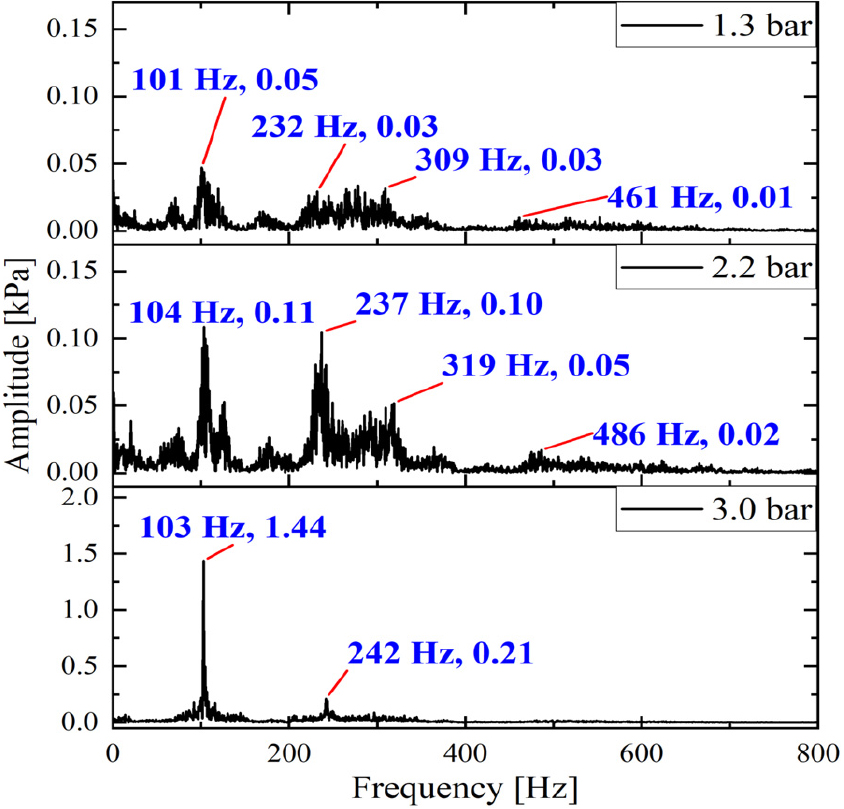
실험으로 측정된 동압 신호와 그 신호의 FFT결과(공진주파수와 진폭)를, EDMD 계산 결과와 비교하였다. 이를 위해 dump 위치에서 측정한 동압의 root mean square (RMS) 값을 Figs. 8, 9, 10에 나타내어 각 조건에서의 성장률과 비교하였다. 또한 동일한 위치에서 측정한 압력 신호로 구한 FFT 결과(공진주파수와 진폭)를 Figs. 11, 12, 13에 각각 나타내었다.
Fig. 8에서 볼 수 있듯이, 혼소율을 변화시켰을 때 1st mode의 성장률과 동압의 RMS 경향은 서로 다른 반면, 2nd mode의 경향은 1st mode에 비해 서로 일치함을 보인다. 또한 압력 섭동은 혼소율 40%에서 가장 큰 값을 보이는 동시에 EDMD 2nd mode에서도 양수의 성장률을 보여 압력 섭동의 증가로 인한 연소불안정이 발생 경향이 상대적으로 높을 것이라고 판단할 수 있다. Fig. 11의 FFT 결과에서도 다른 혼소율 조건과 달리 공진 현상으로 간주할 수 있는 주파수 peak이 관찰되었다. 더불어, 2nd mode의 주파수가 1st mode의 주파수의 2배가 되는 점도 역시 혼소율 40%에서 음향 공진이 야기되는 것을 보여준다. EDMD 기법을 적용하여 음향 공진에 의해 발생한 연소불안정을 감별할 수 있음을 암시한다.
Pilot split ratio를 변경하여 얻은 성장률과 동압의 RMS 값을 Fig. 9에 나타내었다. 압력 섭동은 pilot split ratio가 증가함에 따라 감소하였고 혼소율 변화 경우에서와 마찬가지로 성장률의 경향은 1st mode보다 2nd mode에서 동압의 RMS 경향이 일치했다. 주파수는 실험 측정치와 일치하였다. Fig. 12의 FFT 결과에서 알 수 있듯이 혼소율 40% 조건과 달리 압력 섭동의 진폭이 크지 않았고, 공진주파수가 측정되더라도 실제로 그 주파수에서의 압력섭동은 공진 모드로 전개되지 못했음을 알 수 있다. Pilot split ratio, 15%, 16%에서의 1st mode를 제외하고 모두 성장률이 음수의 값을 가지기 때문에 시간이 지날수록 압력 섭동의 진폭이 감소하여 연소불안정이 발생하지 않을 것으로 예측할 수 있다.
작동 압력을 변화시켜 계산한 EDMD 결과와 동압의 RMS값을 비교한 결과를 Fig. 10에 나타내었다. Fig. 10에서 보듯이, pilot spilt ratio를 변화시켰을 때의 결과와는 다르게, 압력 섭동이 작동 압력에 따라 증가하였다. 이를 EDMD 계산결과와 비교하였을 때, 1st mode와 2nd mode의 성장률이 RMS값 변화 경향과 일치하지 않았지만 3 bar 조건에 한하여 2nd mode의 경향이 유사하게 나타났다. FFT 결과에서도 3.0 bar 조건이 다른 압력 조건에 비해 공진주파수 peak이 명확하게 나타났다. 하지만 EDMD 결과로부터 1st mode와 2nd mode의 성장률이 모두 음수로 계산되었기에 시간이 지날수록 압력 섭동은 지수적으로 감소하여 연소불안정이 발생하지 않을 것으로 예측된다.
4. 결 론
가스터빈의 연소 과정에서 발생한 자발광을 측정하고 그 실험 데이터를 이용하여 EDMD 기법을 적용하였다. 혼소율, pilot split ratio, 작동 압력 변화에 따른 연소불안정성 경향을 판단하고 공진주파수를 계산하여 이를 FFT 결과와 비교하였다. FFT로 계산된 주파수와 EDMD로 계산된 주파수 간의 오차는 작으며 특히, 혼소율 40%에서 2nd mode의 성장률이 양의 값을 보였다. 이를 통해 해당 mode로 인하여 연소불안정이 발생할 것이라고 예측하였고 FFT로 계산된 진폭과 함께 고려하였을 때 EDMD 기법이 연소불안정성 판단에 사용될 수 있음을 보였다. 혼소율 뿐만 아니라 pilot split ratio, 작동 압력을 변화시킨 모든 조건에서 2nd mode의 경향이 동압의 RMS 경향과 일치하였다.
한편, 개선한 점도 파악되었다. 예를 들어, 1st mode의 경향은 일치하지 않았으며, FFT로 계산된 진폭의 크기와 맞지 않는 성장률이 계산되었다. 이러한 오차는 EDMD와 자발광 측정에 내재되어 있는 noise 때문이라고 판단된다. 이를 해결하기 위해 후속 연구에서 empirical mode decomposition(EMD), variational mode decomposition (VMD) 등의 기법으로 데이터의 noise를 줄일 예정이다. 또한, EDMD 기법을 보완하여 물리적으로 의미있는 데이터와 고정확도의 EDMD 기법의 결합을 통해 연소불안정을 예측 정확도를 향상시킬 계획이다.