Application of CMC Model in 0D Simulation of Diesel Engine

Jaesung Kwon; Jeonghyeon Yang; Beomsoo Kim

doi:10.15231/jksc.2021.26.1.041

Preview

Research Article

Journal of The Korean Society Combustion. 31 March 2021. 41-50
https://doi.org/10.15231/jksc.2021.26.1.041

Application of CMC Model in 0D Simulation of Diesel Engine

디젤 엔진 0D 해석을 위한 CMC 모델 응용

Jaesung Kwon¹

Jeonghyeon Yang¹

Beomsoo Kim¹^*

권 재성¹

양 정현¹

김 범수¹^*

¹Department of Mechanical System Engineering, Gyeongsang National University

¹경상국립대학교 기계시스템공학과

^{*Corresponding Author}

ABSTRACT

A numerical analysis of the diesel engine performance and pollutant emissions was conducted by 0D simulation based on the CMC combustion model for turbulent diffusion flames. For the combustion analysis, the CMC model, the skeletal mechanism for n-heptane and the NOx mechanism included in GRI 3.0 were used. The evaporation process of fuel was simulated using the multizone spray model, and the density weighted PDF for the mixture fraction was calculated in real time based on the momentum conservation principle with the empirical models for spray tip velocity. The analysis was conducted by applying a multiple flame structure to the operating conditions of the multi-stage fuel injection method, and the predicted results well matched to the experimental data for the pressure variations. It also shows good qualitative and quantitative results for NOx.

Keywords

Conditional moment closure

Diesel engine

NOx

0D simulation

MAIN

1. 서 론
2. 수치해석 방법
2.1 지배 방정식
2.2 Multizone 분무 모델
2.3 밀도가중 PDF, $F (η)$
2.4 Conditional moment closure(CMC) 모델
2.5 화학반응모델
2.6 엔진규격 및 운전조건
3. 해석결과 및 고찰
3.1 화염구조
3.2 조건평균 스칼라소산율(CSDR)
3.3 연소실 압력
3.4 배기가스제목
4. 결 론

1. 서 론

최근 강화되는 환경규제에 대응하기 위해 내연기관 생산업체는 엔진의 소형화를 비롯하여 연료 분사 기술 및 과급 시스템 개선 등 엔진 성능 향상과 유해 배기가스 저감을 위한 다양한 노력을 이어가고 있다. 내연기관의 설계 및 개발에 있어서 수치 해석은 시간과 비용을 절감하기 위한 좋은 도구이며 시간이 갈수록 그 중요성이 증대되고 있다. 수치 해석은 0D 또는 1D 모델로부터 3D 모델까지 다양한 방법을 이용하며, 오픈소스코드 및 상용소프트웨어를 포함하여 다수의 열유체 수치해석 프로그램이 존재한다.

0D 모델은 수치 해석을 수행하기 위한 계산영역을 설정할 때 연소실을 하나의 계산영역으로 설정하는 single- zone 모델과 연소실을 여러 개의 계산영역으로 나눈 multi- zone 모델로 세분할 수 있다. Single-zone 모델은 연소실 내의 질량과 에너지 보존만을 고려한 해석을 수행하므로 계산 부담이 적다는 장점이 있으나 난류 유동에 의한 온도 및 화학적 조성의 공간 분포에 대한 정보를 얻을 수 없기 때문에 배기 물질 예측에는 한계가 있다[1, 2, 3]. 반면, 3D CFD(Computational Fluid Dynamics) 모델은 비정상 질량, 운동량 및 에너지 보존식에 대한 계산을 수행하여 복잡한 형상에 대한 난류 특성 및 연소, 열전달 등 연소실 내의 물리적 현상에 대한 광범위한 정보를 제공한다. 그러나 계산 비용에 대한 부담 때문에 시스템 레벨에서의 해석 수행에는 한계가 있다.

상기 0D 모델의 근본적인 문제를 개선하기 위해 디젤 연료가 분사된 이후 분무의 침투 거리와 속도에 대한 실험식에 기반한 유사차원해석기법이 개발되었고, 분무 영역을 다수의 zone으로 구분하여 각 zone별로 연료 증발 및 공기와 연료의 혼합 과정에 대한 정보를 획득할 수 있게 되었다. 그러나 초기 multi-zone 모델은 연료가 증발되면 곧바로 연소 반응이 시작된다고 가정함에 따라 배기 예측에는 여전히 한계가 있었다[4, 5, 6]. 이를 극복하기 위해 0D 해석기법에 n-heptane의 상세화학반응에 기반한 Conditional moment closure(CMC) 모델을 적용하여 시험용 디젤 엔진을 대상으로 넓은 범위의 운전조건에 대한 코드 검증이 수행되었다[7, 8, 9]. 여기서 CMC 모델을 다단 분사 조건에 적용하기 위해 각각의 분사에 대해 독립적인 화염 구조를 부여하였으며, 서로 다른 화염 간의 상호 작용은 배제하였다. 이에 따라 연료를 분사할 때마다 각각의 확률밀도함수(Probability density function, PDF)를 계산하여, 화염 그룹별로 화학종의 질량을 계산할 수 있었다. 이는 실제적인 물리현상에는 정확히 부합하지 않기 때문에 국부적인 열유동 해석 정보가 필요할 경우에는 3차원 해석을 통해 보다 정교한 결과를 도출해야 한다.

이 외에도 다양한 연구 그룹에 의해 엔진의 시스템 레벨 해석을 위한 0D 해석이 수행되고 있으며, GT-POWER와 같은 1D 엔진 사이클 해석프로그램에 multi-zone 연소 모델을 결합시켜 상용프로그램의 장점을 최대한 활용하면서 취약한 연소 모델을 보완하거나 다양한 연소 문제에 대해 연구자가 원하는 모델을 채택하여 해석의 정확성을 향상시키기 위한 다수의 연구가 수행되었다[10, 11, 12, 13, 14, 15].

본 연구에서는 연료와 공기의 혼합과정을 보다 정확하게 모사할 수 있도록 분무영역에 유입되는 공기 질량에 대한 모델을 수정하였으며, 배기물질 예측의 정확도를 높이기 위해 조건평균 스칼라소산율(Conditional mean scalar dissipation rate, CSDR)에 대한 모델을 수정하였다. 기존 0D 연소모델과 달리 0D-CMC모델은 연료에 따른 화학반응을 반영하여 실시간으로 개별 화학종의 질량 변화를 계산할 수 있고, 혼합분율에 대한 개별 화학종의 분포를 계산할 수 있다는 장점이 있다. 이를 검증하기 위해 새로운 시험용 엔진을 대상으로 공연비(Air/fuel ratio, A/F)에 대한 parametric study를 수행하였고, 주어진 엔진을 대상으로 다양한 운전 조건에 대해 동일한 모델 상수를 적용하였다.

2. 수치해석 방법

2.1 지배 방정식

0D 해석은 질량과 에너지 보존식만 수치적으로 풀기 때문에 3차원 운동량 보존은 고려되지 않으므로 연소실 내부 혼합기의 열역학적 특성이나 화학적 조성의 공간적인 변화는 알 수 없다.개방형 시스템에 대한 질량 보존은 식 (1)과 같으며, IVC부터 EVO까지의 구간에서는 연료유량만 고려하면 된다.

(1)

\dot{m} = \sum_{i}^{} ({\dot{m}}_{i, \in} - {\dot{m}}_{i, o u t})

위 식에서 첨자 i는 검사면 i를 나타낸다. 연소실 내부 기체의 전체질량에 대한 연료의 질량분율( $f$ ) 변화율과 당량비의 변화율은 각각 식 (2), (3)과 같이 구한다.

(2)

\dot{f} = \sum_{i}^{} (\frac{\dot{m_{i}}}{m}) (f_{i} - f)

(3)

\dot{ϕ} = \frac{1}{ϕ_{s}} \frac{\dot{f}}{{(1 - f)}^{2}}

개방형 시스템의 에너지 보존식은 식 (4)와 같고, 열손실은 연소실 내부 기체와 벽 사이의 대류 열전달과 연료의 증발 잠열 총합으로 식 (5)와 같이 구해진다.

(4)

\frac{d (μ)}{d t} = - P \frac{d V}{d t} + \sum_{i}^{} \dot{Q_{i}} + \sum_{i}^{} h_{i} m_{i}

(5)

\sum_{i}^{} \dot{Q_{i}} = \sum_{i}^{} h_{i} A_{i} (T_{i} - T) - {\dot{Q}}_{f g}

식 (5)에 포함된 열전달 계수 $h$ 는 Hohenberg [16]의 관계식을 이용해 구해지며, 증발 잠열은 Borman과 Johnson [17]의 모델에 의해 구해진다. 식 (4)와 이상기체의 상태방정식을 이용해 연소실 기체의 평균온도 변화율에 대한 식 (6)을 유도할 수 있다[18].

(6)

\frac{d T}{d t} = \frac{(A - \frac{P}{C} (\frac{\partial u}{\partial P}) (\frac{\dot{m}}{m} - \frac{\dot{V}}{V} + \frac{\dot{ϕ}}{R} (\frac{\partial R}{\partial ϕ})) - \frac{\partial u}{\partial ϕ} \dot{ϕ})}{D}

(7)

A = - R T \frac{\dot{V}}{V} + \frac{1}{m} (\sum_{i}^{} \dot{Q_{i}} + \sum_{i}^{} h_{i} \dot{m_{i}} - u \dot{m})

(8)

B = 1 + \frac{T}{R} \frac{\partial R}{\partial T}

(9)

C = 1 - \frac{P}{R} \frac{\partial R}{\partial P}

(10)

C = \frac{\partial u}{\partial T} + \frac{\partial R}{\partial P} \frac{P}{T} \frac{B}{C}

수치적으로는 $\dot{m}, \dot{V}, \dot{Q}, \dot{ϕ,} \dot{T}$ 에 대한 5개의 상미분방정식을 동시에 계산하여 매 time step마다 새로운 $m, V,$ $Q, ϕ, T$ 의 값을 구한 뒤 이상기체의 상태방정식에 대입하여 연소실 평균압력을 구한다.

2.2 Multizone 분무 모델

2.2.1 분무의 영역 분할

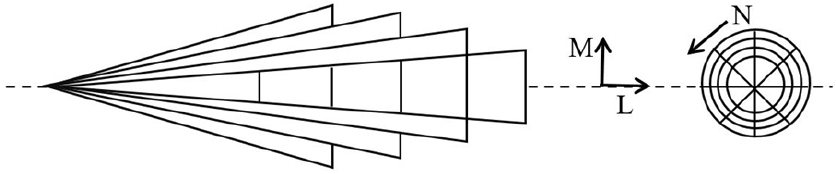
디젤 엔진에서 액체 상태의 연료가 분사되면 Fig. 1에 보이는 것과 같이 분사방향으로 설정된 축방향(L)과 반경방향(M)으로 분무 영역을 분할한다. 이 때 분할 간격 및 총 분무 영역의 개수는 주어진 상황에 따라 달라지나 본 연구에서는 연료의 분사 이후 크랭크각이 0.5° 증가할 때마다 축방향으로 새로운 분무 영역을 하나씩 생성하고, 해당 영역에 대해 반경방향으로는 10개의 세부 영역으로 분할하였다. 따라서 연료의 분사기간이 길어지면 해석에 사용되는 연료의 총 분무 영역 개수가 증가하게 되며, 분무가 연소실 벽에 충돌하는 경우에는 충돌 후 반시계 방위각 방향으로 12개 영역으로 추가로 분할된다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F1.jpg

Fig. 1.

Schematic diagram of spray zoning model.

2.2.2 분무의 도달 거리와 속도

노즐에서 연료가 분사될 때 분무의 초기 속도는 연료 분사율( ${\dot{m}}_{\in j}$ )을 이용해 식 (11)과 같이 계산한다.

(11)

V_{0} = \frac{{\dot{m}}_{\in j}}{ρ_{l} A_{n}}

분무의 도달 거리(S)와 속도(V) 및 미립화 시점(t_b)은 식 (12), (13), (14)와 같다.

(12)

S = 2.95 {(\frac{∆ P}{ρ_{a}})}^{0.25} {(d_{n} t)}^{0.5}

(13)

V (M) = 1.48 {(\frac{∆ P}{_{a}})}^{0.25} d_{n}^{0.5} {[t + t_{b} (1) - t_{b} (M)]}^{- 0.5}

(14)

t_{b} (M) = 28.65 \frac{ρ_{l} d_{n}}{{(ρ_{a} ∆ P)}^{0.5}} \exp [- 8.557 \times 10^{- 3} (M - 1)^{2}]

분무가 벽에 충돌하고 난 후 반경방향의 중심(M=1) 영역에 대한 분무의 도달 거리와 속도는 각각 식 (15), (16)과 같다.

(15)

S (1) = K_{i m p} t^{0.25}

(16)

V (1) = 0.25 K_{i m p} t^{- 0.75}

(17)

K_{i m p} = \frac{S_{i m p} (1)}{{[t_{i m p} (1)]}^{0.25}}

벽 충돌 후 반경방향으로 M번 째 영역의 속도는 식 (18)과 같다.

(18)

V (M) = 0.25 K_{i m p} {[t + t_{i m p} (1) - t_{i m p} (M)]}^{- 0.75}

연소실 내에 스월이 있을 때에는 분무의 진행이 스월의 강도에 큰 영향을 받게 되는데 이 때에는 보정상수(C_s)를 기존의 속도식에 곱하여 식 (19)와 같이 스월의 영향을 반영한다. C_s는 식(20)과 같이 정의된다.

(19)

S_{s} = C_{s} · S

(20)

C_{s} = (1 + \frac{π R_{s} r p m S}{30 V_{0}})

2.2.3 혼합기 형성

연료 분사 후 분무 영역으로 유입되는 공기의 질량은 운동량 보존에 기초하여 식 (21), (22), (23)과 같이 계산한다.

(21)

m_{f} V_{0} = (m_{f} + m_{a}) V

(22)

m_{a} = m_{f} (V_{0} / \frac{d S}{d t} - 1)

(23)

{\dot{m}}_{a, c a l} = C \dot{m_{a}}

식 (23)의 C는 보정 상수로서 벽 충돌 전(C_f)과 후(C_w)에 서로 다른 값을 사용한다. Hiroyasu 등[4]이 제안한 값은 벽 충돌 전에는 $C_{f} = 0.7$ , 충돌 후에는 $C_{w} = 1.5$ 이다. 그러나 성능과 배기 예측의 정확도를 향상시키기 위해 엔진에 따른 최적값을 시행착오적으로 찾아야 하며, 본 연구에서는 광범위한 운전 조건에 동일한 상수를 사용하기 위해 엔진의 운전 조건에 관계된 변수를 조합하여 식 (24)와 (25)의 관계식을 사용하였다.

(24)

C_{f} = \exp [C_{1} \frac{m_{A}}{\sqrt{m_{f, j}}} - C_{2} t_{\in j} \frac{V_{0}}{d_{n}} \frac{(L - 1)}{N_{z o n e}} {(\frac{2500}{r p m})}^{1.2}]

(25)

C_{w} = C_{3}

연료는 액체 상태로 분사되어 미립화 시점에 순간적으로 작은 액적으로 분할된다고 가정하고, 모든 액적의 SMD(Sauter mean diameter, d₃₂)는 식 (26)과 같이 주어진다[19].

(26)

d_{32} = 23.9 (∆ P)^{- 0.135} ρ_{a}^{0.121} B_{f}^{0.131}

2.2.4 연료 증발

연료의 미립화 이후 연소실 내부 기체로부터의 열전달에 의해 연료가 증발하는 과정은 식 (27) , (28), (29)에 의해 모델링된다[17].

(27)

\frac{d m_{f g}}{d t} = π d_{l} N_{z} D_{v} S h \frac{P_{t}}{R_{v} T_{m}} \ln (\frac{P_{t}}{P_{t} - P_{v}})

(28)

\frac{d T_{l}}{d t} = \frac{1}{m_{l} C_{p l}} (q - λ \frac{d m_{f g}}{d t})

(29)

q = π d_{l} N_{z} k_{m} (T_{a} - T_{l}) N (\frac{z}{e^{z} - 1})

2.3 밀도가중 PDF, $F (η)$

공간적분된 형태의 밀도가중 PDF( $F (η)$ )와 혼합분율( $η$ )은 각각 식 (30), (31)와 같이 정의된다.

(30)

F (η) = \int_{V_{c}}^{} \bar{ρ} \tilde{P} (η) d V

(31)

η = \frac{m_{f g}}{m_{f g} + m_{a}}

식 (30)에서 $\tilde{P} (η)$ 는 Favre PDF로서 $η$ -공간 [0, 1]에서 적분된 값은 1이다.

2.4 Conditional moment closure(CMC) 모델

화학종 i에 대한 조건평균 질량분율 Q_i는 혼합분율 $ξ$ 에 대해서 식 (32)와 같이 정의된다.

(32)

Q_{i} (η, t) = < Y_{i} (t) | ξ (t) = η >

위 식에서 Y_i는 화학종 i에 대한 질량분율이고, $η$ 는 혼합분율의 표본변수이다. $< | >$ 은 혼합분율에 대한 Y_i의 조건평균을 의미한다. ISR (Incompletely stirred reactor)[20] 가정 하에서 공간 적분된 형태의 CMC 지배방정식은 식(33), (34)과 같다.

(33)

\frac{\partial Q_{i}}{\partial t} = < N | η > \frac{\partial^{2} Q_{i}}{\partial η^{2}} + < w_{i} | η >

(34)

\frac{\partial Q_{h}}{\partial t} = < N | η > \frac{\partial^{2} Q_{h}}{\partial η^{2}} + <\frac{1}{ρ η} \frac{\partial p}{\partial t} | η>

1차 CMC 모델에 대한 조건평균 반응률( $< w_{i} | η >$ )은 식 (35)과 같이 조건평균 질량분율과 엔탈피의 함수로 모델링된다.

(35)

< w_{i} | η > ≃ w_{i} (Q_{1}, \dots, Q_{n}, Q_{h})

조건평균 스칼라소산율은 AMC(Amplitude mapping closure)[21] 모델에 의해 식 (36)와 같이 모델링하였다.

(36)

< N | η > = C_{s d r} \exp (- 2 {[e r f^{- 1} (2 η - 1)]}^{2})

위 식에서 erf는 error function을 나타낸다. 3D해석과 달리 0D 코드에서는 유동장을 계산하지 않기 때문에 stoichiometric 혼합분율에서의 CSDR은 식 (37)과 같이 모델링하였다.

(37)

< N | η = ξ_{s t o i} > = C_{4} \frac{V_{0}}{d_{n} R_{s}^{0.5}} \exp [- C_{5} \frac{C A - C A_{s o i, j}}{r p m^{0.6}}]

식 (36)에 포함된 상수 C_sdr은 식 (36)와 (37)로부터 구할 수 있다.

0D CMC-ISR 모델은 복수화염구조 모델로 확장되었으며, 각 화염그룹의 밀도가중 PDF 역시 독립적으로 정의된다. 화염그룹 j에 속한 화학종 i의 Favre 평균 질량분율( $\tilde{Y_{i j}}$ )과 연소실 내부에 존재하는 화학종 i의 전체질량( $M_{i}$ )은 각각 식 (38)과 (39)에 의해 계산된다.

(38)

\tilde{Y_{i j}} = \int_{0}^{1} \tilde{P_{j}} (η) Q_{i j} (η) d η

(39)

M_{i} = \sum_{j}^{} \int_{0}^{1} F_{j} (η) Q_{i j} (η) d η

2.5 화학반응모델

CMC 계산에 필요한 화학종들의 조건평균 반응률은 skeletal chemistry를 이용하여 CHEMKIN 서브루틴에 의해 계산된다. 본 연구에서 사용된 n-heptane의 반응 메커니즘은 44개의 화학종에 대해 저온 및 고온에서의 반응을 모두 고려한 112개의 화학반응으로 구성되어 있고[9], GRI 3.0[22]의 NOx 메커니즘이 추가되었다. 연료의 증발과 공기와의 혼합과정 계산에서는 n-dodecane의 물성치[17]를 사용하였다.

2.6 엔진규격 및 운전조건

Table 1과 2는 본 연구에서 모사된 엔진규격과 운전조건을 나타낸다. Case 1-6의 운전 조건은 모두 동일한 엔진 속도(2500 rpm) 및 출력을 가지며, A/F와 EGR rate에 따른 parametric study를 위한 조건들로 구성된다. 본 연구에 사용된 컴퓨터의 CPU는 Intel® Core™ i9-9900k (3.6 GHz) 모델이며 단일 코어를 사용하여 4회의 연료 분사 조건에 대해 총 계산 시간이 평균 3분을 넘지 않는다. 화학반응이 사용된다는 점을 고려했을 때 이는 획기적인 결과이며 0D 해석의 정확성만 향상된다면 시스템 레벨 해석에서 굉장히 유용하게 활용될 것으로 기대된다. Table 3은 본 연구에서 사용된 분무 혼합 및 조건평균 스칼라소산율에 대한 모델 상수를 나타낸다.

Table 1.

Specifications of the test engine

Displacement volume	396 cm³
Clearance volume	4 cm³
Stroke	8.45 cm
Bore	7.72 cm
Connecting rod	14.0 cm
Fueling system	Common rail
IVC	-146° ATDC
EVO	134° ATDC

Table 2.

Engine operating conditions

CASE	1	2	3	4	5	6
A/F	18.7	20.0	21.4	22.7	24.0	25.5
EGR [%]	33.4	33.2	31.5	29.2	26.8	23.5

Table 3.

Model constants

C₁ (mixing)	1.5
C₂ (mixing)	5.0 × 10^-6
C₃ (mixing)	0.38
C₄ (CSDR)	1.5 × 10^-5
C₅ (CSDR)	7.2

주어진 6개의 운전 조건에 대해 동일한 모델 상수를 사용하여 일관된 해석을 수행하였으며, 모델 상수의 최적값은 시행착오적으로 탐색해야 한다.

3. 해석결과 및 고찰

3.1 화염구조

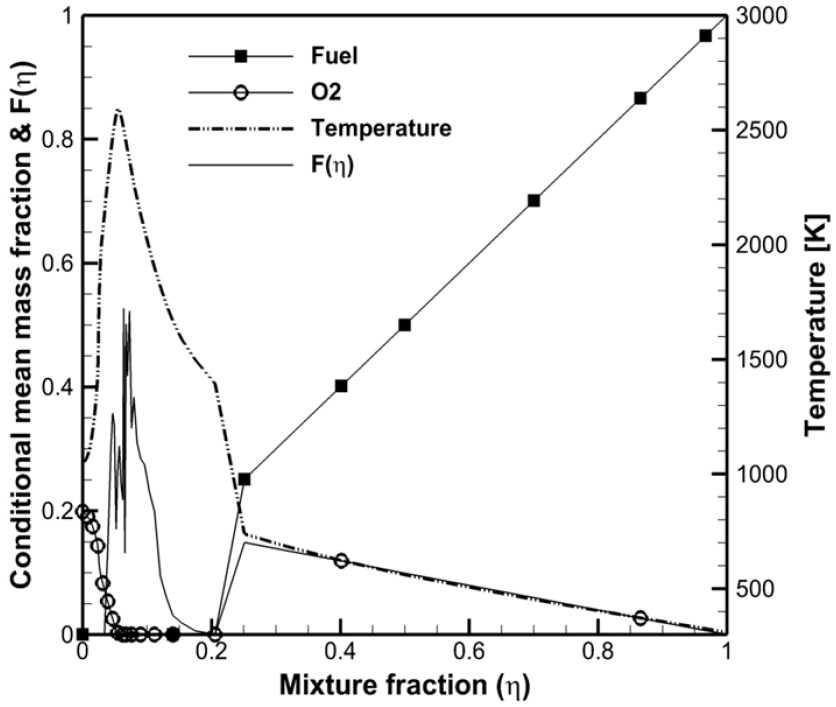
연소실 내부 화학종의 질량은 식 (39)와 같이 계산되며, Fig. 2는 case 6의 크랭크각이 18.3 °ATDC 일 때, 화염구조를 나타낸다. $η$ -공간에서 조건평균 온도는 stoichiometric 혼합분율 부근에서 최대값을 나타내고, 연료와 산화제 모두 이론과 부합하는 분포를 보여준다. 밀도가중 PDF의 경우 그래프가 부드러운 형태로 나타나지 않는데 이는 전체 분무영역의 개수가 충분하지 않기 때문이며 분무영역의 개수를 증가시킬수록 보다 부드러운 밀도가중 PDF를 구할 수 있다. 본 연구에 사용된 multizone 분무 모델의 한계를 극복하기 위해서는 3D CFD에서 사용되는 β-PDF 등의 적용이 필요할 것으로 판단된다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F2.jpg

Fig. 2.

Flame structure and density weighted PDF, $F (η)$ .

3.2 조건평균 스칼라소산율(CSDR)

CSDR은 실험값을 구할 수 없기 때문에 주어진 엔진에 대해 식(37)과 같은 모델의 직접적인 검증이 어렵다. 따라서, 연소실 압력이나 배기물질의 질량을 실험값과 비교하여 간접적으로 오차가 최소가 되는 최적의 모델 상수를 시행착오적으로 선택하게 되며, 이 점이 3차원 CMC 해석과 연소모델 측면에서 달라진 점이다. 0D CMC 모델을 이용한 유사차원해석에 있어서 다양한 분무 및 연소모델에 포함된 모델상수 보정은 시간이 걸리기는 하지만 주어진 엔진에 대해 동일한 모델상수를 적용하기 때문에, 넓은 범위의 다양한 운전 조건에 대해 일관된 해석이 수행된다는 장점이 있다.

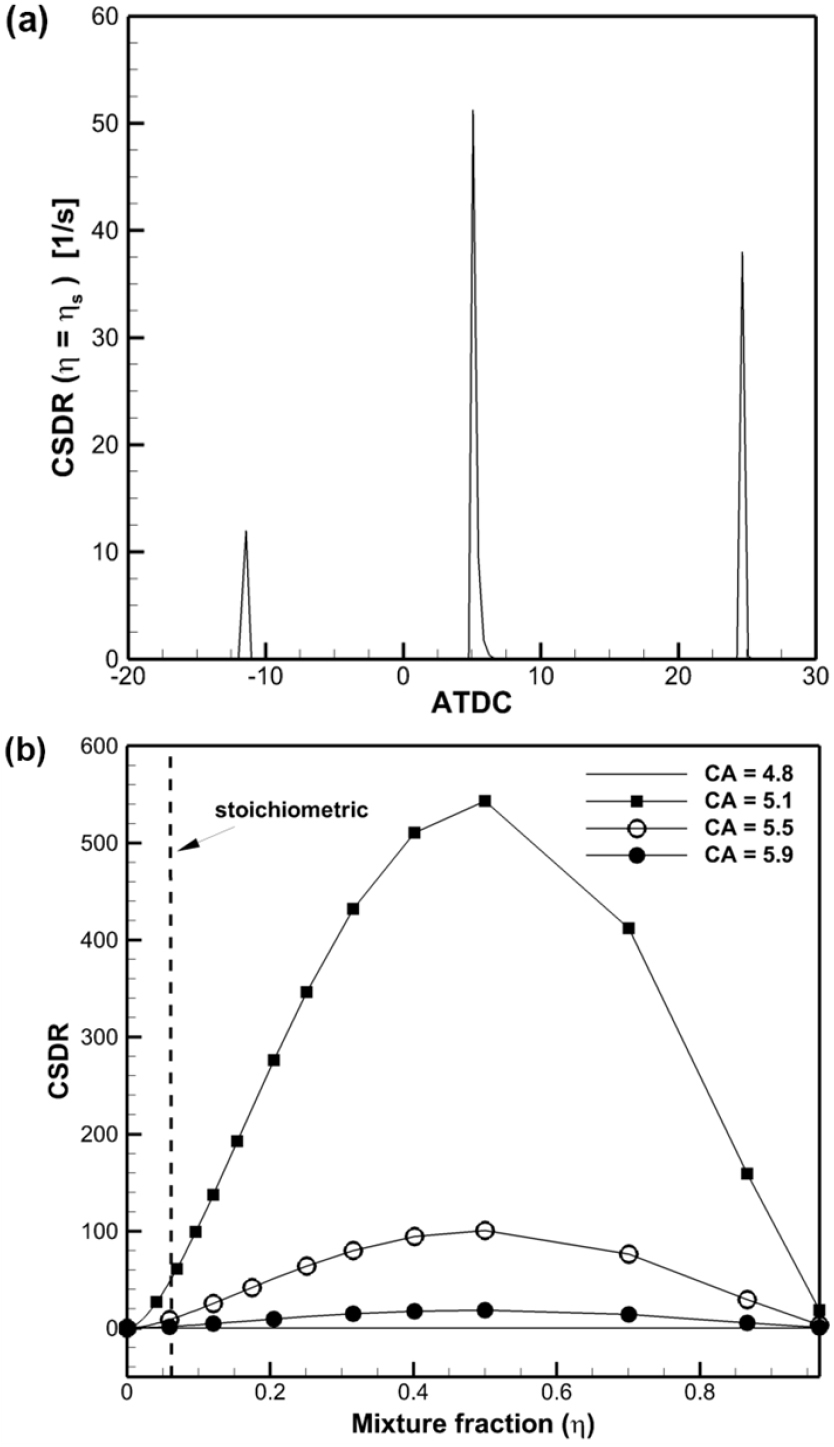
Fig. 3(a)는 분사된 연료 분무와 기체가 혼합되는 과정에서 시간에 따라 주어진 분무 영역의 혼합분율이 변화할 때, 전체 분무 영역 중 stoichiometric 혼합분율을 가지는 분무 영역에서의 CSDR 변화를 나타낸다. CSDR의 절대값은 연료가 분사된 이후 짧은 시간동안 급격히 증가했다가 0에 수렴하는 것을 알 수 있다. Fig. 3(b)는 $η$ -공간에서 식 (36)에 의한 CSDR 분포를 나타내는데, 연소실 내부 압력과 배기 예측에 있어서 중요한 영역은 바로 stoichiometric 혼합분율 부근의 CSDR 값이다. 그 이유는 stoichiometric 혼합분율 부근에서 연소반응이 활발하게 일어나 조건평균 온도가 높아지기 때문이여, 화학종별 질량 계산시 밀도가중 PDF도 혼합이 진행됨에 따라 stoichiometric 혼합분율 부근에서 높은 값을 나타내기 때문이다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F3.jpg

Fig. 3.

The (a) temporal variation of conditional mean scalar dissipation rate at stoichiometric mixture fraction and (b) distribution of conditional mean scalar dissipation rate with respect to mixture fraction for case 6.

3.3 연소실 압력

Fig. 4는 0D 해석에 사용된 6개 운전 조건의 연소실 압력에 대한 실험값과 해석결과를 비교한 것으로서 해석결과가 정성적·정량적 측면에서 모든 조건에 대해 실험값에 잘 부합하는 결과를 보여준다. Case 1의 경우 2번 째 분사 후 점화가 지연되며 계산된 압력이 실험값보다 낮게 나타나는데, 0D CMC모델에서 점화지연은 CSDR과 저온 화학반응 메커니즘을 포함한 CMC 계산의 영향을 받는다고 판단되며, 대부분의 열방출은 비예혼합 연소과정에서 발생하기 때문에 multizone 분무 모델에 기반한 혼합계산 결과인 밀도가중 PDF의 정확도가 압력 계산 결과에 더 큰 영향을 미친다. 모델 검증에 사용된 시험엔진의 운전 조건은 다단 분사를 채택하여 파일럿 분사를 2회 실행한 뒤 본분사가 시작되며 이후 후분사를 1회 포함하여 총 4회의 연료분사가 수행된다. 3번 째 연료분사가 시작되기 전 2회의 파일럿 분사과정에서 형성된 연료공기 혼합영역은 점화가 시작되는 순간부터 동시다발적으로 연소 반응이 일어나면서 압력 선도에 매끄럽지 못한 부분이 나타날 수 있는데, 현재의 복수화염 구조에서는 서로 다른 화염 구조 간의 상호작용은 허용하지 않으므로 일정 부분 한계를 가지고 있다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F4.jpg

Fig. 4.

Measured and calculated pressure traces at different A/F and EGR rates.

또한, 모든 조건에 대해 후분사가 시작된 후 해석결과에서 보여주는 3번 째 피크압력 형성 또한 현재 복수화염 모델의 한계로 인식된다. 그러나 3차원 CFD와 달리 0D 해석의 목적이 시스템 레벨 해석 측면에서 단기간에 총량 관점의 빠른 해석 결과를 도출하는 것이기 때문에 그 목적에 비추어 볼 때는 현재 적용된 0D CMC모델의 일관된 해석 결과가 실용적인 면에서 기대효과가 크다고 볼 수 있다. 본 연구에서 사용된 계산 조건은 A/F 증가에 따른 parametric study의 가능 여부를 진단하기 위한 것인데, 현재 도출된 압력 선도를 보았을 때 엔진 제원 및 형상과 운전 조건에 대한 정보만 적절하게 주어진다면 0D 해석을 엔진성능 및 배기특성 예측 도구로 사용할 수 있다고 판단되며, 모델 개선 및 타 엔진에 대한 추가 검증을 통해 추후에 정확도 및 효율성에 대한 개선연구가 수행될 예정이다.

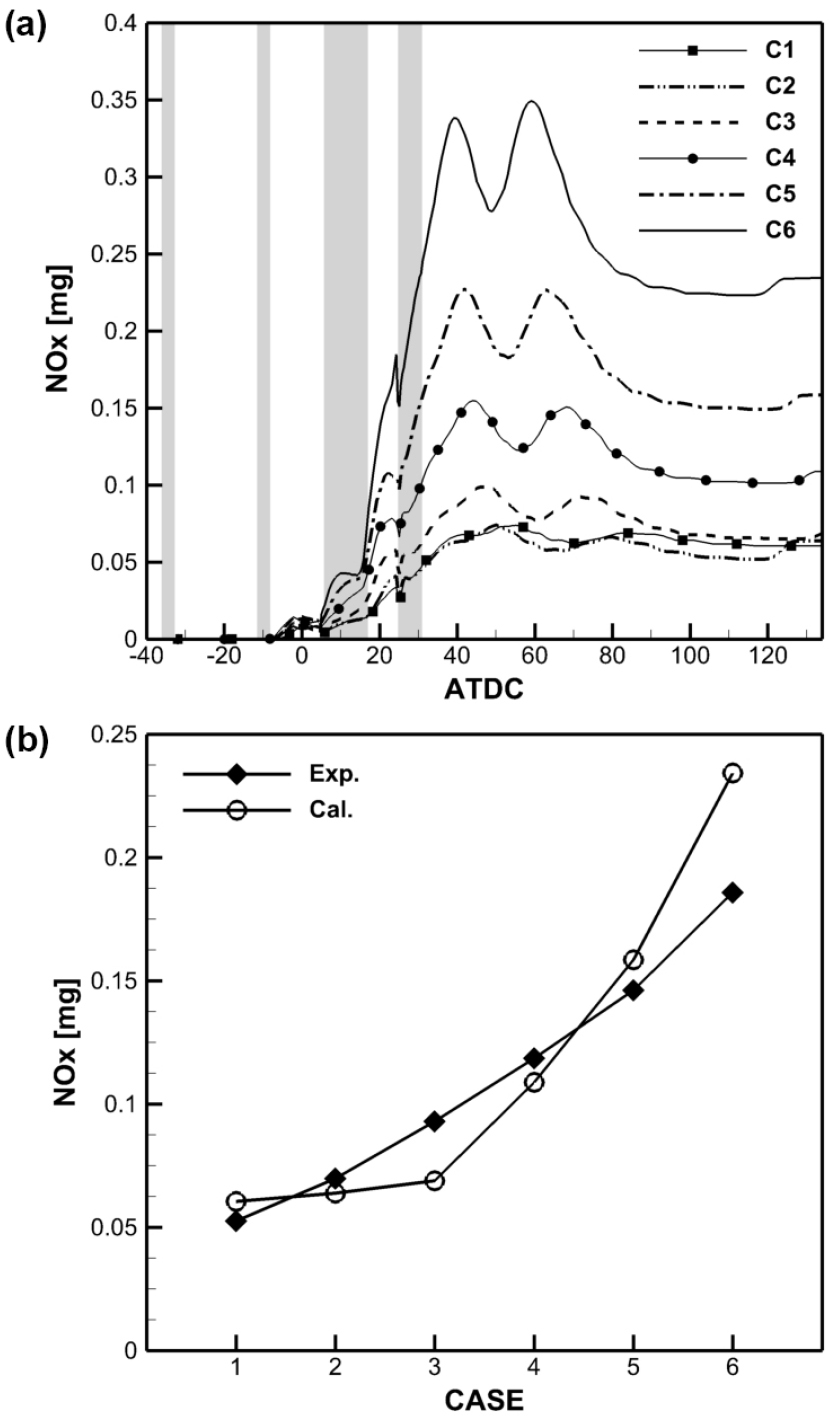
3.4 배기가스

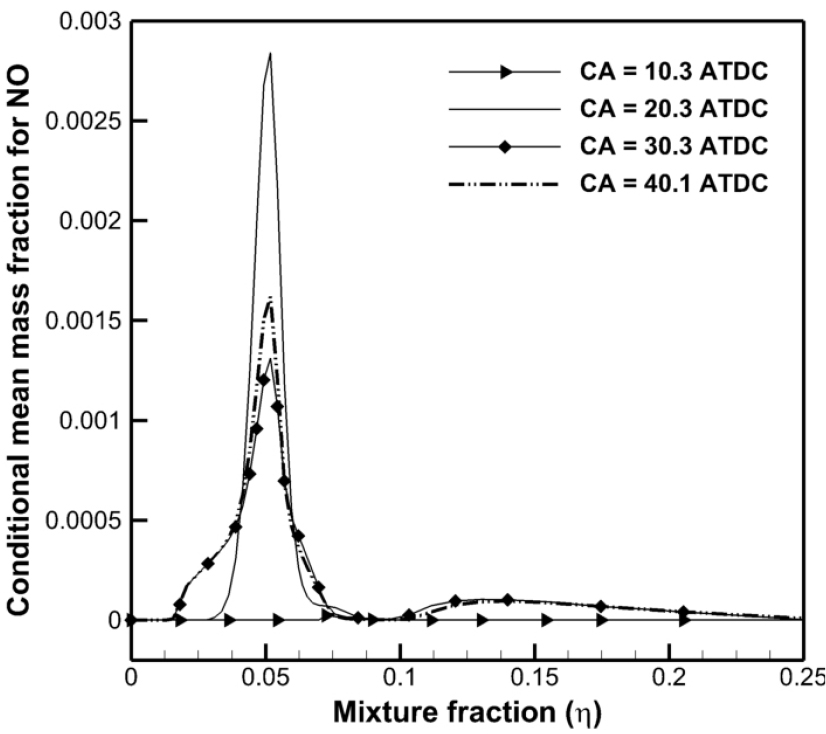
0D CMC 모델은 n-heptane에 대한 상세화학반응을 채용하여 시간에 따른 개별 화학종의 생성량 변화를 계산할 수 있다. Fig. 5는 case 6에 대해 $η$ -공간에서 시간에 따라 NO의 분포가 변화되는 과정을 4개의 크랭크각에 대하여 나타내었다. Stoichiomeric 혼합분율은 약 0.062이며, 이 부근에서 평균적인 NO의 질량분율이 높다는 것을 알 수 있으며, 혼합분율이 0.25보다 큰 영역에서는 NO의 질량분율이 거의 0에 가까운 정도로 미미하여 나타내지 않았다. Fig. 6(a)는 NOx의 총발생량을 크랭크각의 변화에 대해 나타낸 것으로 두 번째 파일럿 분사 이후 NOx가 의미있게 발생하다가 본분사 이후 급격히 증가하게 되며 후분사 이후 최대값을 보인다. 이와 같은 시간에 대한 배기 물질 변화를 파악할 수 있다는 점이 상세화학반응을 채택한 장점이며 연소반응이 종료된 이후 평형과정에 도달하는 과정에서 NOx의 감소 경향을 알 수 있다. 크랭크각이 120 °ATDC를 지나면서 NOx발생량이 증가하는 이유는 밀도가중 PDF의 영향이라고 파악되며, 이를 개선하기 위해서는 분무 모델 개선 및 정교한 상수보정이 요구된다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F5.jpg

Fig. 5.

Conditional mean mass fraction of NO for case 6.

https://static.apub.kr/journalsite/sites/kosco/2021-026-01/N0590260105/images/ksssf_26_01_05_F6.jpg

Fig. 6.

The (a) temporal variation of NOx emissions and (b) comparison between measured and calculated NOx.

Fig. 6(b)는 EVO에서 NOx의 총생성량에 대해 실험값과 해석결과를 비교한 것으로, A/F증가에 따른 NOx 증가를 정성적으로 잘 나타낸다. 또한, 정량적으로도 NOx 생성을 잘 예측한다는 것을 알 수 있는데, 이는 압력 선도의 예측에서도 짐작할 수 있는 부분이다. 다만, 국부적인 NOx발생 분포에 대한 정보를 얻을 수 없는 것이 0D 해석의 한계이므로 공간에 대한 상세한 해석 결과가 요구되는 경우에는 3D 해석을 수행해야만 한다. 0D CMC모델에서 제일 취약한 부분이 CSDR에 대한 모델링인데, 배기물질 총량을 계산함에 있어 CSDR의 영향이 크게 작용하므로 이는 반드시 개선해야할 부분으로 보인다.

4. 결 론

본 연구에서는 디젤엔진의 성능 및 배기특성 예측을 위해 수정된 분무 모델을 기반으로 CMC모델을 0D 해석에 적용하여 범용성을 입증하고자 하였으며 아래의 결론을 도출하였다.

1) 0D CMC모델을 통해 다양한 범위의 운전 조건에 대한 일관된 해석이 가능하며, 이를 통해 연소실 압력 및 배기물질 생성량에 대한 정량적 해석결과 도출이 가능하다.

2) 주어진 엔진에 대한 최소한의 실험데이터를 이용해 모델을 보정할 수 있고, 이를 통해 엔진의 다양한 운전 조건에 대한 parametric study가 가능하다.

3) 다중화염구조로 연료의 다단분사 과정을 모사할 수 있으나 압력 선도가 매끄럽지 못한 부분이 발생한다.

4) CSDR모델의 물리적 기반이 취약한 부분과 밀도가중 PDF 계산방식의 한계를 확인하였다.

상기에 도출된 결과를 기반으로 향후 분무모델 및 CSDR모델 개선을 위한 후속 연구가 수행될 예정이며, 이를 전제로 0D CMC모델의 실용성을 높일 수 있을 것으로 기대된다.

기호설명

Alphabet

A/F : air/fuel ratio

EGR : exhaust gas recirculation

EVO : exhaust valve opens

IVC : inlet valve closes

N : scalar dissipation rate

PDF : probability density function

Q_i : conditional mean mass fraction of species i

Q_ij: conditional mean mass fraction of species i of the flame structure j

Q_h: conditional mean enthalpy

Rs : swirl ratio

S : spray tip penetration

Greek letters

$η$ : mixture fraction

ρ : density

$ϕ$ : equivalence ratio

Subscripts

a : air

f : fuel

Acknowledgements

본 연구는 미래창조과학부 생애 첫 연구사업의 일환(NRF-2017R1C1B5017704)으로 수행되었습니다.

References

D.E. Foster, An Overview of Zero-Dimensional Thermodynamic Models for IC Engine Data Analysis, SAE Technical Paper 852070, 1985. 10.4271/852070

N. Watson, A.D. Pilley and M. Marzouk, A Combustion Correlation for Diesel Engine Simulation, SAE Technical Paper 800029, 1980. 10.4271/800029

L. Ning, A Cycle Simulation Program for the Dynamic Operation of a Single Cylinder Direct Injection Diesel, University of Wisconsin-Madison, 1988.

H. Hiroyasu, T. Kadota, M. Arai, Development and use of a spray combustion modeling to predict diesel engine efficiency and pollutant emissions: Part 1 combustion modeling. Bulletin of JSME, 26(214), (1983) 569-575. 10.1299/jsme1958.26.569

H. Hiroyasu, K. Nishida, Fuel Spray Trajectory and Dispersion in a D.I. Diesel Combustion Chamber, SAE Technical Paper 890462, 1989. 10.4271/890462

T. Yoshizaki, K. Yuzaki, H. Hiroyasu, H. Yamasita, K. Kaneda, M. Suzuki, Model Verification of the Evaporating Diesel Spray Distribution in the Combustion Chamber of a D.I. Diesel Engine, SAE Technical Paper 962054, 1996. 10.4271/962054

J. Kwon, J. Seo, D. Lee and K.Y. Huh, Zero- dimensional simulation of diesel engine combustion and emissions based on CMC model and skeletal reaction mechanism, SAE Int. J. Engines, 4(1), (2011) 964-975. 10.4271/2011-01-0845

A.Y. Klimenko, R.W. Bilger, Conditional moment closure for turbulent combustion, Prog. Energy Combust. Sci., 25(6), (1999) 595-687. 10.1016/S0360-1285(99)00006-4

S. Liu, J.C. Hewson, J.H. Chen, H. Pitsch, Effects of strain rate on high-pressure nonpremixed n-heptane autoignition in counterflow, Combustion and flame, 137(3), (2004) 320-339. 10.1016/j.combustflame.2004.01.011

K. Narayanaswamy, C.J. Rutland, Cycle Simulation Diesel HCCI Modeling Studies and Control, SAE Technical Paper 2004-01-2997, 2004. 10.4271/2004-01-2997

K. Inagaki, M. Ueda, J. Mizuta, K. Nakakita, S. Nakayama, Universal Diesel Engine Simulator (UniDES): 1st Report: Phenomenological Multi-Zone PDF Model for Predicting the Transient Behavior of Diesel Engine Combustion, SAE Technical Paper 2008-01-0843, 2008. 10.4271/2008-01-0843

A. Dulbecco, F.A. Lafossas, T.J. Poinsot, A 0D Phenomenological Approach to Model Diesel HCCI Combustion with Multi-Injection Strategies Using Probability Density Functions and Detailed Tabulated Chemistry, SAE Int. J. Engines, 2(1), (2009) 548-568. 10.4271/2009-01-0678

A. Bhave, M. Kraft, L. Montorsi, F. Mauss, Modelling a Dual-Fuelled Multi-Cylinder HCCI Engine Using a PDF Based Engine Cycle Simulator, SAE Technical Paper 2004-01-0561, 2004. 10.4271/2004-01-0561

R. Zhao, D. Wen, W. Li, W. Zhuge, Y. Zhang, Y. Yin, Characteristic and regulation method of parallel turbocompound engine with steam injection for waste heat recovery. Energy, 208, (2020) 118422. 10.1016/j.energy.2020.118422

L. Xiang, G. Theotokatos, H. Cui, K. Xu, H. Ben, Y. Ding, Parametric knocking performance investigation of spark ignition natural gas engines and dual fuel engines. Journal of Marine Science and Engineering, 8(6), (2020) 459. 10.3390/jmse8060459

G.F. Hohenberg, Advanced Approaches for Heat Transfer Calculations, SAE Technical Paper 790825, 1979. 10.4271/790825

G.L. Borman, J.H. Johnson, Unsteady Vaporization Histories and Trajectories of Fuel Drops Injected into Swirling Air, SAE Technical Paper 620271, 1962. 10.4271/620271

E.E. Streit, G.L. Borman, Mathematical Simulation of a Large Turbocharged Two-Stroke Diesel Engine, SAE Technical Paper 710176, 1971. 10.4271/710176

H. Hiroyasu, T. Kadota, Fuel Droplet Size Distribution in Diesel Combustion Chamber, SAE Technical Paper 740715, 1974. 10.4271/740715

J. Seo, Y. Lee, I. Han, K.Y. Huh, H. Kim, Extended CMC Model for Turbulent Spray Combustion in a Diesel Engine, SAE Technical Paper 2008-01-2411, 2008. 10.4271/2008-01-2411

E.E. O'Brien, T.L. Jiang, The conditional dissipation rate of an initially binary scalar in homogeneous turbulence, Phys. Fluids A: Fluid dynamics, 3(12), (1991) 3121-3123. 10.1063/1.858127

G.P. Smith, D.M. Golden, M. Frenklach, N.W. Moriarty, B. Eiteneer, M. Goldenberg, C.T. Bowman, R.K. Hanson, S. Song, W.C. Gardiner Jr, V. V. Lissianski, Z. Qin. GRI-MECH 3.0, http://www.me. berkeley.edu/gri_mech/.

Journal of The Korean Society CombustionISSN:1226-0959(Print) 2466-2089(Online)한국연소학회

Preview

Application of CMC Model in 0D Simulation of Diesel Engine

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

Fig. 1.

Schematic diagram of spray zoning model.

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

Table 1.

Specifications of the test engine

Table 2.

Engine operating conditions

Table 3.

Model constants

Fig. 2.

Flame structure and density weighted PDF, F(η).

Fig. 3.

The (a) temporal variation of conditional mean scalar dissipation rate at stoichiometric mixture fraction and (b) distribution of conditional mean scalar dissipation rate with respect to mixture fraction for case 6.

Fig. 4.

Measured and calculated pressure traces at different A/F and EGR rates.

Fig. 5.

Conditional mean mass fraction of NO for case 6.

Fig. 6.

The (a) temporal variation of NOx emissions and (b) comparison between measured and calculated NOx.

Acknowledgements

References

Flame structure and density weighted PDF, $F (η)$ .