1. 서 론

탄화수소 연료의 가스화 및 열분해를 통해 얻어진 합성가스는 지구온난화와 화석연료 고갈문제를 대체하는 연료로 널리 사용되어왔다. 합성가스연료의 주요 성분은 H₂와 CO로 이루어져 있으며 그 외에 적은 양의 CO₂, N₂, H₂O, CH₄ 등이 존재하게 되는데, 이 성분은 가스화 및 열분해 공정에 따라 다르게 존재하게 된다. 합성가스를 실제 연소기에 적용하기 위해서는 연료 조성에 따른 화염 안정성 및 오염 물질 배출을 고려하여 최적의 연소조건을 찾아야 한다. 이를 위해 주요 성분비에 따른 층류 연소속도, 화학반응속도, 점화 지연시간과 같은 화염의 기본 특성을 이해하기 위한 많은 연구가 진행되었다[1, 2, 3].

한편 충돌제트 화염은 벽 표면으로의 높은 대류 열전달율과 열효율로 산업용 보일러 및 제철소 내 가열로, 유리(glass) 성형 등과 같은 대규모 산업공정에서부터 가정용 보일러 및 가스스토브와 같이 소규모 열 설비까지 널리 적용되고 있다. 이런 배경으로 이전 연구에서는 연소조건 및 연소기 구조에 따른 열손실, 충돌판의 온도분포와 같은 열전달(heat transfer) 특성과 화염형상 및 가연한계, 화염대 부근의 화학적 반응과 같은 화염특성에 관한 기본적인 연구가 많이 진행되었다[4, 5, 6, 7, 8]. 본 연구팀에서도 합성가스연료를 적용한 충돌제트 버너를 이용하여 연료조성비, 당량비(equivalence ratio, Φ), 레이놀즈수(Reynolds number, Re) 등 다양한 연소조건에서 화염안정화, 열전달, 화염구조와 같은 연소특성에 관한 연구를 수행하였다[9,10, 11] 그런데 충돌제트 화염은 노즐 상부에 위치한 충돌판으로 인해 좀 더 낮은 당량비에서 디스크 형태의 평면화염으로 존재하게 되며, 이는 NOx 제어 및 최소화에 유리하나 낮은 당량비로 연소하게 되면 노즐출구와 충돌판 사이에서 열음향적 불안정성(thermoacoustic instability, TAI)이 발생하게 된다.

열음향 불안정성은 특정한 연소조건 및 형상에 따라 다양한 연소기들에서 자주 발생되는 현상으로, 특징으로는 화염의 형상이 불안정해지고 큰 압력섭동과 소음이 발생하게 된다. 이러한 현상은 결과적으로 연소시스템의 수명단축과 손상으로 이어져 안전사고를 유발할 수 있다. 물체에 충돌되는 평면의 제트화염은 충돌구조로 인해 자려진동(self-oscillation)에 의한 소음이 발생하게 되는데, 충돌판 부근에서 화염의 생성과 소멸 과정이 반복됨에 따라 생긴 압력교란이 노즐로 전달되어 버너 내 혼합기의 속도섭동이 일어나게 되고 이 속도섭동이 다시 노즐출구로 전파되는 순환구조가 된다. 이러한 커플링(coupling) 과정을 되먹임 기구(feedback mechanism)[12]라고 하는데, E. C. Fernandes 등은 충돌판과 노즐간 거리에 따라 다르게 나타나는 평면화염의 진동조건을 안정화선도(stability map)를 통해 구분하였고, 소음특성과 화염의 이미지, 노즐출구에서 발생하는 와류의 개수 등을 이용하여 발생 현상을 모델링하였다[13, 14]. Schuller 등은 화염에서 발생하는 열 방출섭동과 압력섭동을 비교하여 조사하였고, 충돌판과 노즐출구 사이의 거리에 따라 화염의 형상이 달라지고 소음의 강도와 주기성 또한 달라지는 것을 확인하였다[15, 16].

본 연구팀에서도 H₂와 CO의 비율이 10:90인 모사 합성가스연료의 평면 충돌화염을 통해 소음이 없는 구간을 silent flame(SF, Regime I), 소음이 발생하는 구간을 noisy flame(NF, Regime II)으로 구분하였고, noisy flame 영역을 다시 Regime II-1과 II-2로 구분하였다. 또한 스트로우홀 수(Strouhal number)와 당량비, 레이놀즈수로 영역별 소음의 특징을 특성화 하였다[17. 18, 19]. 그런데 이전 연구에서는 유독 연소소음이 심하게 발생하는 구간(Regime II)과 이 영역에서 다양한 소음현상을 발견하였으나, 이러한 거동이 단일 연료가 아닌 혼합 연료인데다가 10 %로 수소함량이 비교적 적은 합성가스의 조성비 차이에 의한 현상인지가 명확하지 않아 수소함량이 높은 경우에서 추가적인 분석이 요구되었다.

이에 본 연구에서는 조성비가 다른 조건에서도 이전 연구에서와 같은 연소불안정으로 심한 소음이 동반되는 현상을 검증하고 이에 따른 차이점을 조사하고자 종전의 조성비에서 수소함량을 높여 H₂:CO = 50:50로 설정하였다. 이 경우 수소함량이 증가함에 따라 영역별로 더욱 명확해진 화염형상과 압력섭동 신호를 통해 자려진동의 연소불안정성을 동역학적 모드분석법이 포함된 다양한 방법으로 분석한다.

2. 실험장치 및 실험방법

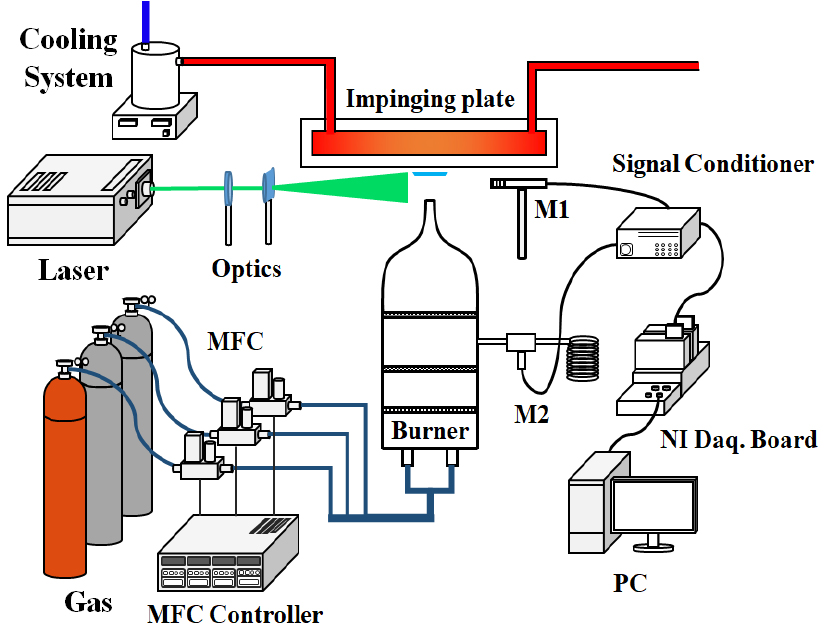
본 연구에서 사용한 실험장치의 개략도를 Fig. 1에 나타내었다. 버너의 전체 길이는 200 mm이며 노즐출구의 직경은 10 mm이다. 역화방지 및 균일한 유동을 형성하기 위해 높이 1/3과 2/3 지점의 버너 내부에 가는 메쉬(mesh)를 장착하였다. 또한, 버너 상부는 교축비가 36인 헬름홀츠 형상의 수축형 노즐(contraction nozzle)로 제작하였고, 화염에 의한 예열효과를 최소화하고자 노즐 출구를 가급적 날카롭게 가공하였다. 충돌판은 고온의 화염으로 인한 표면 응축수 생성과 과열을 방지하기 위하여 약 333.15 ± 3 K의 냉각수를 0.7 L/min으로 흘려주었으며, K-type 열전대를 이용하여 충돌판의 온도가 333.15 ± 3 K로 유지되는 것을 실시간으로 확인하였다. 외부 유동에 의한 교란을 최소화하기 위해 버너와 충돌판 주위로 아크릴 쉴드(acrylic shield)를 설치하였다.

Fig. 1.

Schematic diagram of an impinging jet burner and experiment equipments.

화염의 이미지와 유동장 이미지는 비디오카메라(Sony, FDR AX700)을 이용하여 960 fps로 촬영하였으며, 이 중 유동장 이미지는 0.05 μm 알루미나 산란입자와 2 W 아르곤레이저의 단면 광을 이용한 Mie-scattering 방식으로 취득하였다. 버너 내부 압력섭동(inner pressure)은 버너 출구 기준 100 mm 하단에 정압 홀을 가공하여 압력형 마이크로폰(PCB Co. 106B, M2)을 장착시켰고, 압력신호의 노이즈 및 음향반사를 고려하여 long line damping tube를 사용한 후 측정하였다. 버너 외부 디스크 화염에서 방출되는 압력섭동(outer pressure)은 Free-field형 마이크로폰(PCB Co. 378B02, M1)으로 측정하였으며, 마이크로폰 과열 및 손상을 고려하여 디스크 화염과 동일한 높이에서 반경 방향으로 100 mm 떨어진 지점에서 측정하였다.

이처럼 버너 안과 바깥 두 군데에서 취득된 압력 데이터는 시그널 컨디셔너(PCB Co. 482C)를 사용하여 보정을 한 후 데이터 수집기(NI Daq Board, NI 9234 Module)와 Signal express 2015 프로그램으로 취득 및 저장을 하였다. 취득률(sampling rates)은 10000 Hz로 4초 동안 측정을 하였고 그 후 Matlab 프로그램을 이용하여 주기성, 소음의 강도(dB) 등 압력정보를 정밀하게 분석하였다.

연료는 99.95%의 고순도 수소와 일산화탄소를 사용하였으며, 산화제는 99.995%의 고순도 공기를 사용하였다. 노즐출구와 충돌판 사이의 거리는 이전 연구와 동일하게 H/d = 2.0로 고정을 하였고 당량비(equivalence ratio, Φ)와 레이놀즈수(Reynolds number, Re_D)에 따른 진동화염의 특징을 조사하였다. 이 경우 관찰한 당량비와 레이놀즈수의 범위는 소음이 발생하는 구간과 층류 조건을 고려하여 각각 Ф = 0.5 ~ 1.0, Re_D = 800 ~ 2500 에서 조사하였으며 이와 같은 주요 변수들을 Table 1로 요약하여 정리하였다.

3. 결과 및 고찰

3.1 안정화선도(stability map)

합성가스의 성분비를 H₂:CO = 50:50로 변경 한 결과, 충돌제트 버너에서 나타난 부상된 디스크 화염에서의 연소소음은 이전 연구와는 달리 총 4개의 구간(Regime)으로 구분할 수 있었고, 본 절에서는 디스크화염의 안정화선도를 통하여 소음이 발생한 구간을 간단히 설명하고자 한다.

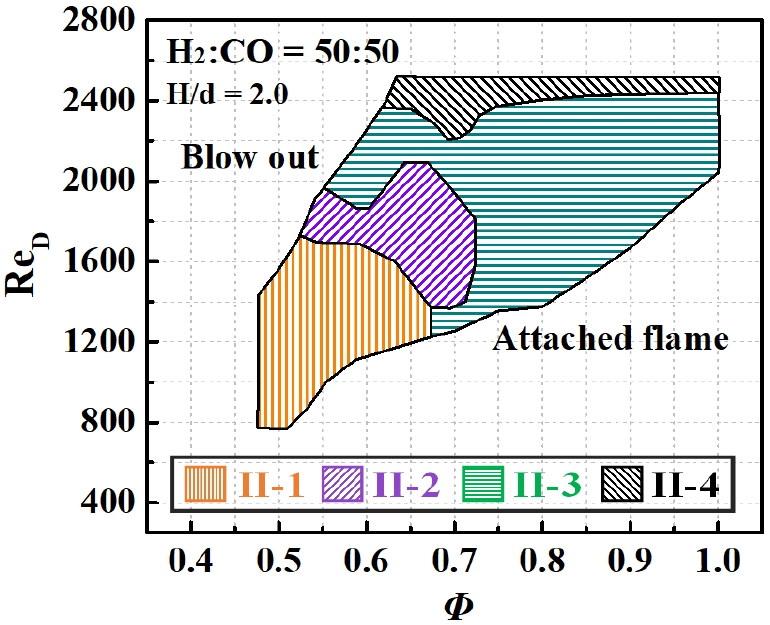
Fig. 2는 H₂:CO = 50:50 조건에서 당량비와 레이놀즈수에 따른 충돌제트 화염에서의 화염안정 및 불안정한 영역들을 보여주고 있다. 높은 유속조건으로 인해 화염이 생존하지 못하는 조건들을 Blow out 구간으로 나타내었고, 화염이 노즐 팁에 부착되어 있는 조건들은 Attached flame 구간으로 분류하였다. 이러한 구간들은 본 연구가 부상된 디스크 화염에서 발생하는 열음향 불안정성을 목표로 하고 있기 때문에 여기에서는 제외하였다. 본 연구의 관심사인 디스크 화염에서 연소소음을 동반하는 연소 불안정성의 영역들을 총 4개의 구간(regime)으로 정의하였는데, Regime II-1, Regime II-2 같은 경우는 이전 연구와 동일하게 각각 하나의 지배적인 주파수(dominant frequency)로 일정한 주기를 가지며 진동하는 구간을 Regime II-1, 지배적인 주파수와 이 주파수를 중심으로 작은 주파수를 가지며 불균일하게 진동하는 구간을 Regime II-2로 정의하였다[17, 18, 19]. 본 연구에서 새롭게 정의한 구간인 Regime II-3은 Regime II-1과 동일하게 하나의 지배적인 주파수로 진동을 하지만 화염 과 유동장의 형상, 주파수 및 소음의 강도(dB, decibel)의 경향이 Regime II-1과 달라 새롭게 정의한 구간이다. 그리고 Regime II-4 는 높은 레이놀즈수로 인하여 생긴 천이(transition)구간의 영향을 받는 곳이다. 이와 같이 4개 구간으로 나눈 기준에 대해서는 다음 절에서 상세하게 기술된다.

Fig. 2.

Flame stability map with equivalence ratio and Reynolds number.

3.2 화염 및 유동장 가시화

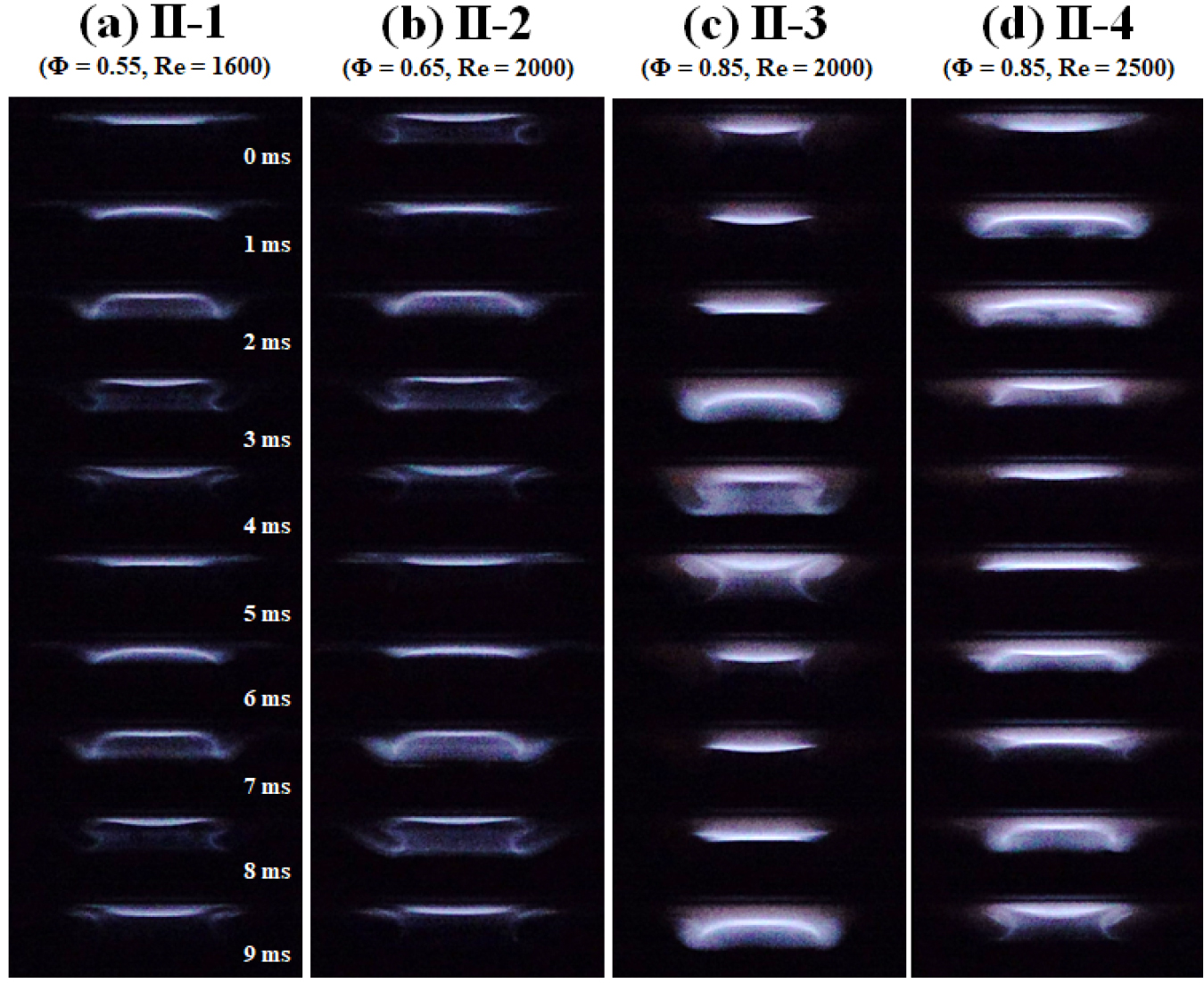
본 절에서는 각 Regime별 대표 조건에서 화염 및 유동장의 형상을 통하여 구분한 기준에 대해 설명하고자 한다. 먼저, Fig. 3는 각 Regime별 대표 조건에서 따른 화염의 직접 형상들을 1 ms의 시간 간격으로 나타내었다. 먼저 (a) II-1과 (c) II-3은 일정한 주기로 화염이 진동하는 것으로는 유사하지만 (a) II-1에 비해 (c) II-3에서 화염의 날개 부분의 생성과 소멸이 더 크게 일어나는 것을 볼 수 있다. 이는 노즐출구에서 발생하는 와류의 크기가 큰 것과 연관 되는 현상으로 Fig. 4에서 부가적으로 설명이 된다. (b) II-2는 (a) II-1과 다르게 화염의 주기가 비교적 불규칙한 주기를 갖는 것을 알 수 있다. (d) II-4는 (c) II-3과 비슷하게 거동하는 것처럼 보이나 화염의 표면에 주름이 생기고 찌그러진 것을 확인할 수 있다. 이는 높은 레이놀즈수로 인하여 천이유동 조건의 영향을 받아 생긴 현상으로 사료된다.

Fig. 3.

Visualization of flame images of each regime in time; (a) II-1(Φ = 0.55, Re_D = 1600), II-2(Φ = 0.65, Re_D = 2000), II-3(Φ = 0.85, Re_D = 2000), II-4(Φ = 0.85, Re_D = 2500).

Fig. 4.

Flame and flow field images for each regime visualized using the Mie-scattering method; (a) II-1(Φ = 0.55, Re_D = 1600), (b) II-2(Φ = 0.65, Re_D = 2000), (c) II-3(Φ = 0.85, Re_D = 2000), (d) II-4(Φ = 0.85, Re_D = 2500).

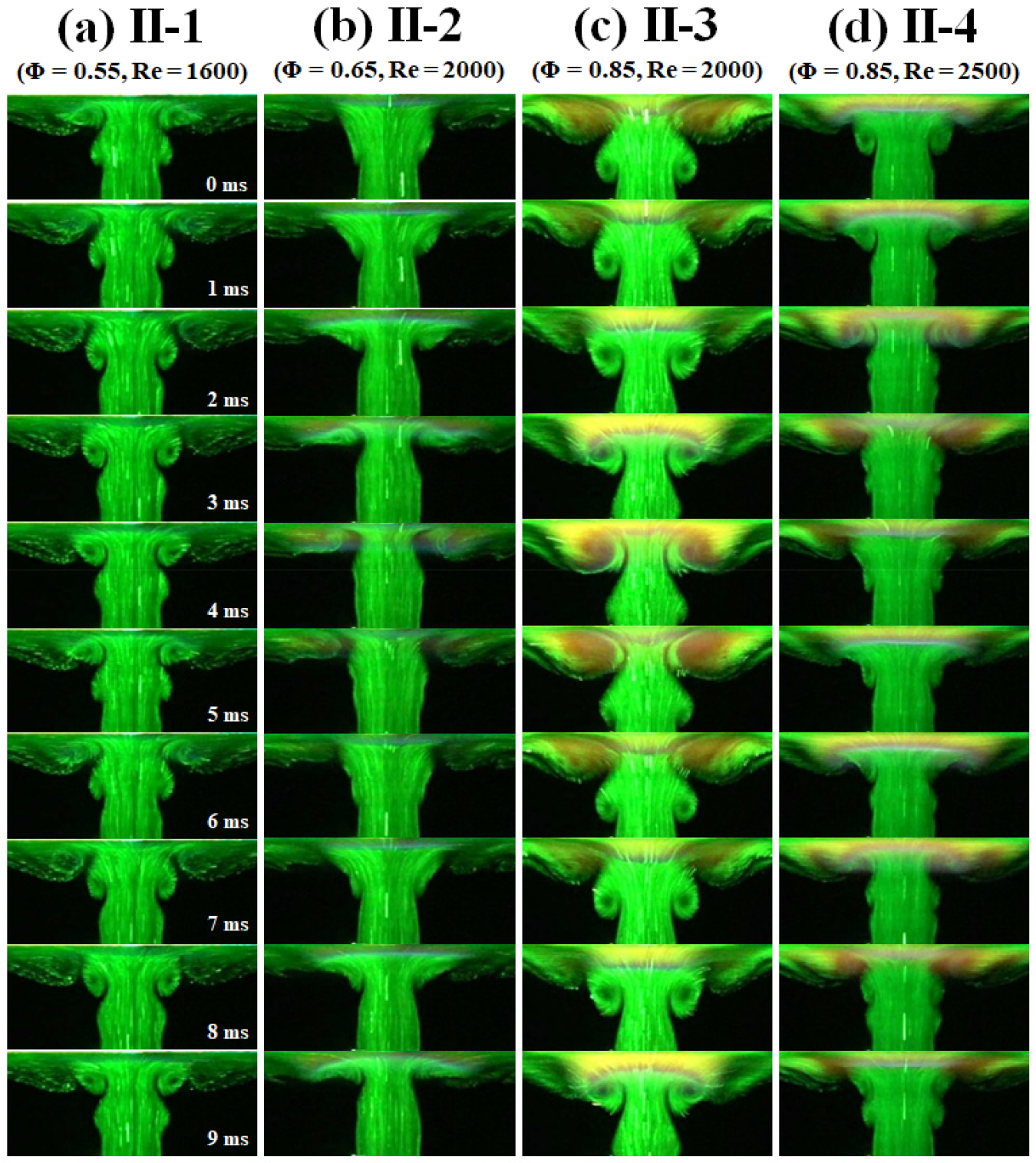
Fig. 4은 Mie-scattering 방법을 이용하여 각 Regime별 대표 조건의 유동장을 보여주고 있다. (a) II-1, (c) II-3에서는 균일한 와류(vortex)가 명확하게 생성된 후 화염으로 전파하는 것을 확인할 수 있지만 (a) II-1의 경우는 노즐출구와 충돌판의 중심 부분부터 와류가 생성되기 시작하여 디스크 화염 부근에서 와류 형상이 점차적으로 없어지는 반면, (c) II-3의 경우는 노즐출구에서부터 강한 와류가 생성된 후 화염부근에서 와류의 형상이 급격하게 팽창하며 소멸되는 것을 볼 수 있다. 와류가 시작되는 지점과 화염 부근에서 소멸하는 과정을 확인해 본 결과, (a) II-1과 (c) II-3은 서로 다르게 거동하고 있음을 확인하였고 Fig. 2의 안정화선도에서 확인할 수 있듯이 당량비 변화에 상당히 민감한 것을 볼 수 있다. 또한 (c) II-3은 합성가스 조성비가 H₂:CO = 10:90 인 이전 연구에서는 나타나지 않은 새로운 소음발생 영역 및 화염구조이다[17, 18, 19]. 즉, 합성가스 조성비와 당량비의 변화가 진동소음의 Regime을 구분하는 주된 원인으로 판단되며, 이러한 이유에 대해서는 추후 계속된 연구로 원인을 파악하여 보고할 예정이다. 이에 비해 (b) II-2와 (d) II-4는 노즐출구에서 일정 지점부터 두 개 이상의 와류가 생성되며 특히 (d) II-4인 경우 다소 불규칙적으로 생성되는 것을 볼 수 있다.

이처럼 Mie-scattering 방법을 이용하여 유동장과 화염의 형상을 확인해 본 결과, 노즐출구에서 생성되는 와류의 형상이 화염에 직접적인 영향을 미치는 것을 알 수 있다.

3.3 압력섭동 특징

앞 절에서 시간에 따른 화염형상과 유동장 분석에 이어 압력섭동에 대한 분석을 통하여 진동하는 화염별 차이점을 확인하고자 본 절에서는 각 Regime별 대표 조건에서 연소불안정이 발생한 압력섭동의 특징들을 조사하였다.

먼저, 장치 공명에 의한 영향을 배제하기 위하여 본 연구에서 사용한 실험장치인 헬름홀츠(Helmholtz) 형상의 버너의 공진주파수(fH)를 식 (1)을 통하여 계산하였다.

여기서 c는 음속으로 c=(kRT)1/2로 나타낼 수 있고, A는 노즐 목의 단면적, V0는 버너의 부피, Lc는 유효 목 길이(effective neck length)로 곡선 형태의 헬름홀츠 공진기는 목 길이를 Lc=L+1.5r으로 보정하여 사용한다[20, 21]. 해당 버너에서 공기가 유체로 작동할 때 공명 주파수의 이론값은 fH = 151 Hz이며, 실제 노즐 출구에 유동을 흘려주었을 때에도 152 Hz의 공명음이 발생하였다. 공기가 아닌 Syngas의 Φ = 0.5 ~ 1.0에 해당하는 물성치를 이론값에 대입하였을 때 ± 5 Hz 차이로 크게 차이가 없음을 사전에 확인하였다. 이러한 공진주파수는 본 연구의 반응장에서 발생하는 주파수들(145 ~ 200 Hz)과는 무관하며 버너에 의한 공명현상이 연소 반응장에는 영향이 없음을 확인하였다.

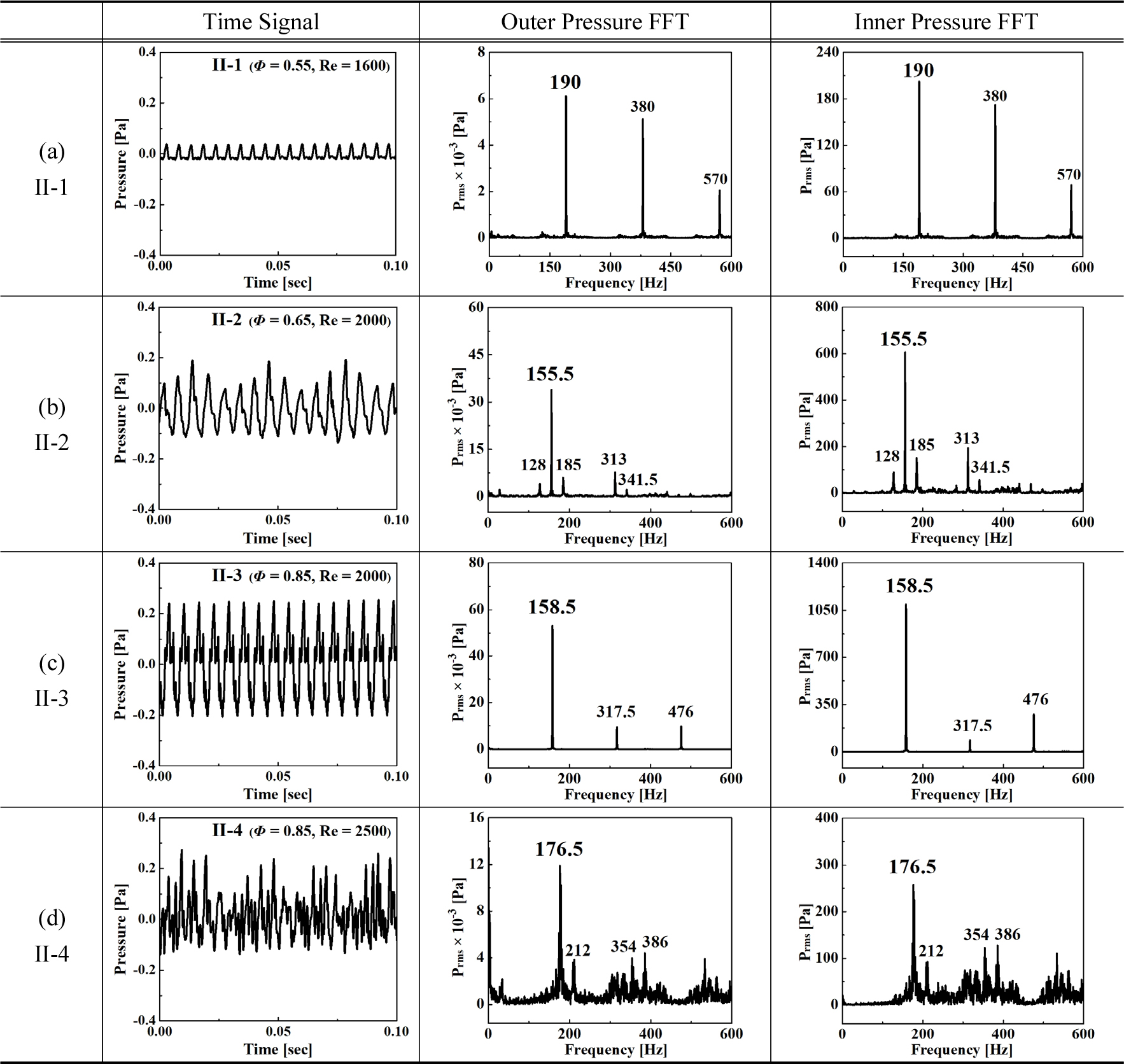
Time signal, FFT로 나타낸 각 Regime별 대표 조건의 압력섭동 결과 값을 Fig. 5에 나타내었다. Time signal은 4초 동안 측정한 40000개의 데이터 중 0 ~ 0.1초에 해당하는 압력 데이터로 소음의 파형이 육안으로도 구분되는 것을 볼 수 있다. Outer pressure FFT는 화염의 진동으로 인해 방출되는 압력섭동을 취득 후 FFT 변환을 한 데이터이고, inner pressure FFT는 화염에서 발생하는 압력섭동이 버너 내부로 전파하여 생기는 버너 내부의 압력변동 데이터이다.

Fig. 5.

Analysis of pressure fluctuation data for representative conditions for each regime using time signal and FFT; (a) II-1(Φ = 0.55, Re_D = 1600), II-2(Φ = 0.65, Re_D = 2000), II-3(Φ = 0.85, Re_D = 2000), II-4(Φ = 0.85, Re_D = 2500).

먼저, (a) II-1인 경우 화염에서 방출되는 압력섭동이 time signal을 통하여 일정하게 진동하는 것을 확인할 수 있으며, FFT 변환 결과 버너 내 외부 값이 ƒ = 190 Hz인 동일한 주기로 진동하고 그 외의 주파수는 정수배의 값으로(2ƒ, 3ƒ) 조화주파수(harmonic frequency)로 존재하는 것을 볼 수 있다. 영향력이 제일 큰 주파수를 지배적인 주파수(dominant frequency, ƒ_d)라고 정의하였고, 2ƒ_d, 3ƒ_d와 같은 조화주파수는 비선형 시스템(Nonlinear system)에서 주로 나타나는 성질이 비슷한 주파수이므로 분석에는 제외하였다. 자세히 보면 time signal에서 사인곡선(sine curve)의 정현파가 아닌 다소 복잡한 파형을 형성하고 있지만 FFT 결과는 명확하게 나온 것을 확인할 수 있다. 이는 노이즈가 아닌 조화주파수의 존재로 인해 생긴 결과로 판단된다[22].

(b) II-2는 기본적으로 사인(sine)의 정현파 형상을 띄고 있지만 다소 일그러진 형태를 time signal을 통하여 확인할 수 있으며, FFT 분석 결과 155.5 Hz의 지배적인 주파수와 이를 중심으로 다른 작은 주파수들이 같이 존재하는 것을 볼 수 있다. 이처럼 지배적인 주파수를 제외한 작은 주파수들을 잔여주파수(remainder frequency, ƒ_r)로 정의하였다. 이들 주파수의 특징은 지배적인 주파수(ƒ_d = 155.5 Hz)와 주파수의 차이(ƒ_s = 28.5 Hz)만큼 양 옆으로 존재하는 구조, 즉 지배적인 주파수(155.5 Hz) 양 옆으로 ƒ_d+ƒ_s = 185 Hz, ƒ_d-ƒ_s = 128 Hz의 형태로 존재하는 것을 알 수 있다. 이를 일반적으로 동적 시스템에서는 맥놀이(beating) 현상이라고 한다[23, 24]. 이러한 맥놀이 주파수는 화염뿐만 아니라 버너 내부로 전파된 것을 Inner Pressure FFT로 확인할 수 있으며, (b) II-2 중 모든 조건에서 이와 같은 현상이 발생하였고, 화염과 유동장의 형상에는 영향이 있었지만 지배적인 주파수에는 큰 영향 없이 일정한 경향을 확인하였다.

(c) II-3 같은 경우 비교적 높은 레이놀즈수와 당량비에서 나타나는 구간으로 (a) II-1과 동일하게 하나의 지배적인 주파수로 거동하였지만, 앞 절에서 설명한 바와 같이 화염 형상과 유동장에서 차이뿐만 아니라 다른 주파수 형태로 거동하는 것을 볼 수 있으며 이에 대해서는 다음 절에서 자세하게 설명된다.

(d) II-4의 time signal은 (b) II-2와는 다르게 지저분한 파형을 볼 수 있으며, 이는 유동조건이 관내 유동에서 천이유속 조건으로 인해 생긴 현상으로, FFT 결과에서도 지배적인 주파수가 가장 크게 나타났지만 주변에 노이즈(noise)성 파형들도 다수 존재하는 것을 볼 수 있다. 모든 조건에서 outer와 inner pressure가 동일한 지배적인 주파수로 거동하는 것을 확인하였고, 이는 화염에서 방출되는 압력섭동이 버너 내부유동에 직접적인 영향을 미치고 있는 것을 알 수 있다.

지금까지는 각 Regime별 대표 조건에서 유동 가시화와 압력섭동의 FFT 분석을 통해 부상된 디스크 화염들의 불안정성에 대해서 살펴보았는데, 이처럼 소음이 동반된 진동화염을 동역학적(dynamic)으로 분석하는 방법인 모드 분석법(mode analysis)으로서 위상궤적법인 phase portrait와 궤적의 주기성을 시각화한 recurrence plot 방법을 사용하여 각 Regime별 형상과 차이점을 분석하고자 한다.

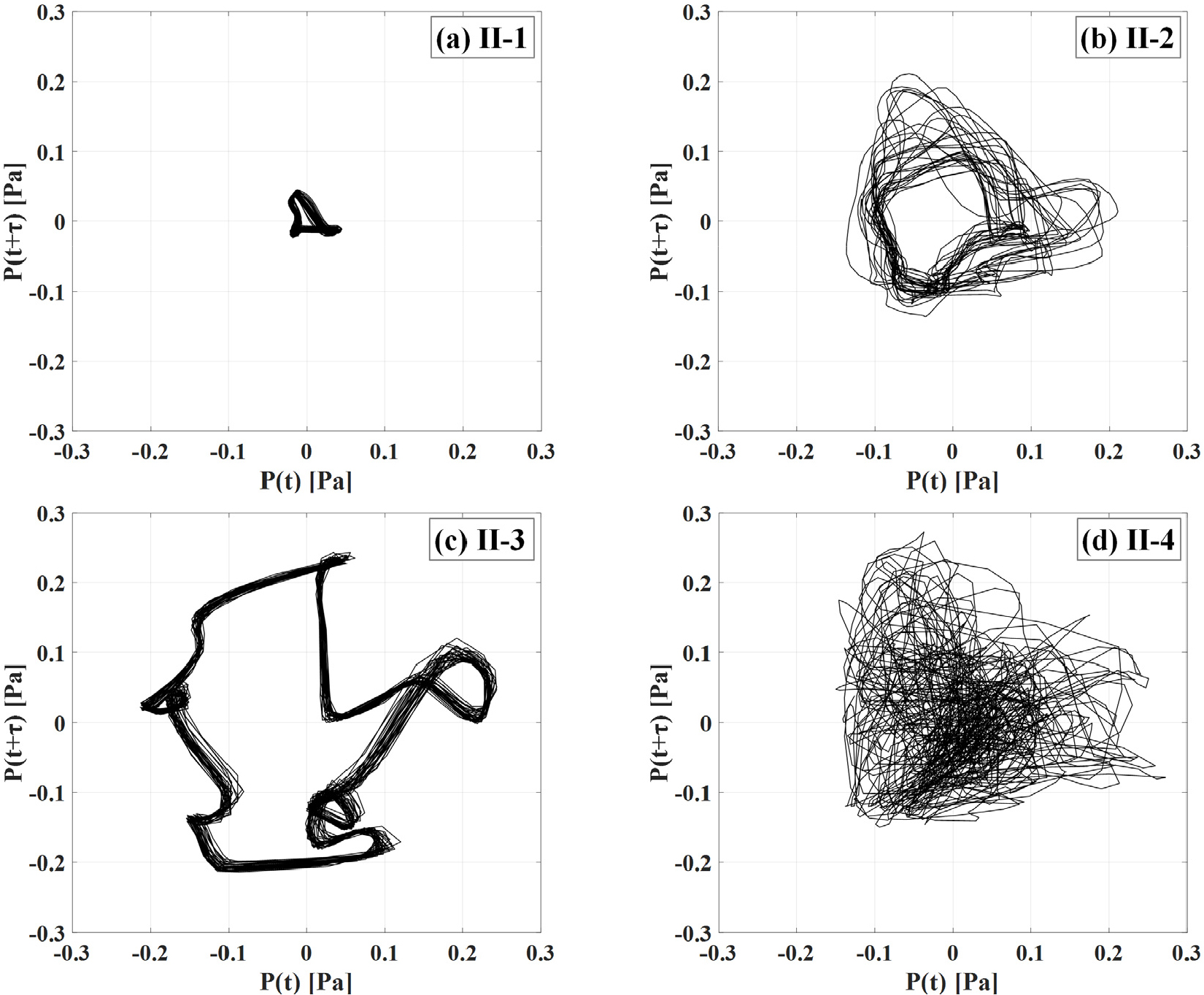
먼저 위상 궤적도(phase portrait) 방법으로 분석한 각 Regime별 압력섭동의 결과 값을 Fig. 6에 나타내었다. 위상 궤적도는 특정 시간에 해당하는 동적 신호 P(t)와 일정한 τ의 위상차를 적용한 동적 신호 P(t+τ)를 이용하여 표현하는 방법으로, 본 연구에서는 하나의 주파수로 거동하는 선형 시스템 및 맥놀이 주파수로 거동하는 비선형 시스템의 주기적인 거동의 차이를 시각적으로 확인하기 위하여 사용하였다[25]. 이 경우 위상차는 뚜렷한 그래프 형상을 확인하기 위하여 각 지배적인 주파수의 한 주기의 1/4에 해당하는 시간(τ=1/4fd)를 적용하였고, 0 ~ 0.2 초에 해당하는 압력 데이터를 이용하여 나타내었다.

Fig. 6.

Pressure fluctuation analysis of representative conditions of each regime using phase portrait method; (a) II-1(Φ = 0.55, Re_D = 1600), (b) II-2(Φ = 0.65, Re_D = 2000), (c) II-3(Φ = 0.85, Re_D = 2000), (d) II-4(Φ = 0.85, Re_D = 2500).

Fig. 6 중 하나의 지배적인 주파수로 거동하는 (a) II-1와 (c) II-3는 비록 거동 패턴(모드)은 서로 다르나 각각 일정한 형상이 반복적으로 뚜렷하게 생성되어 단일 어트랙터(attractor)로 거동하는 것을 알 수 있다. 하나의 주파수로 거동하는 기본적인 정현파일 경우에는 완벽한 원형의 형태로 표현되는 것이 일반적이나 복잡한 형상이 생기는 이유는 앞서 말한 조화주파수의 존재로 인하여 생긴 결과이다[23]. (b) II-2는 지배적인 주파수에 따라 패턴이 다르게 반복되고 흐트려져 있는 것을 확인할 수 있어, 이는 지배적인 주파수와 잔여 주파수가 같이 존재하여 다수의 어트랙터들로 운동되고 있음을 보여주며, (d) II-4는 관내유동 중 천이유동 조건으로 인하여 역시 많은 어트랙터들이 관여된 거동으로 다소 지저분한 형상으로 나타났다. 이처럼 위상궤적을 추적한 분석을 통해서도 서로 다른 4가지 모드의 거동을 보여줌으로써 Fig. 2의 안정화선도에서 나타난 4가지 불안정한 구간의 존재와 특징들을 확인할 수 있었다.

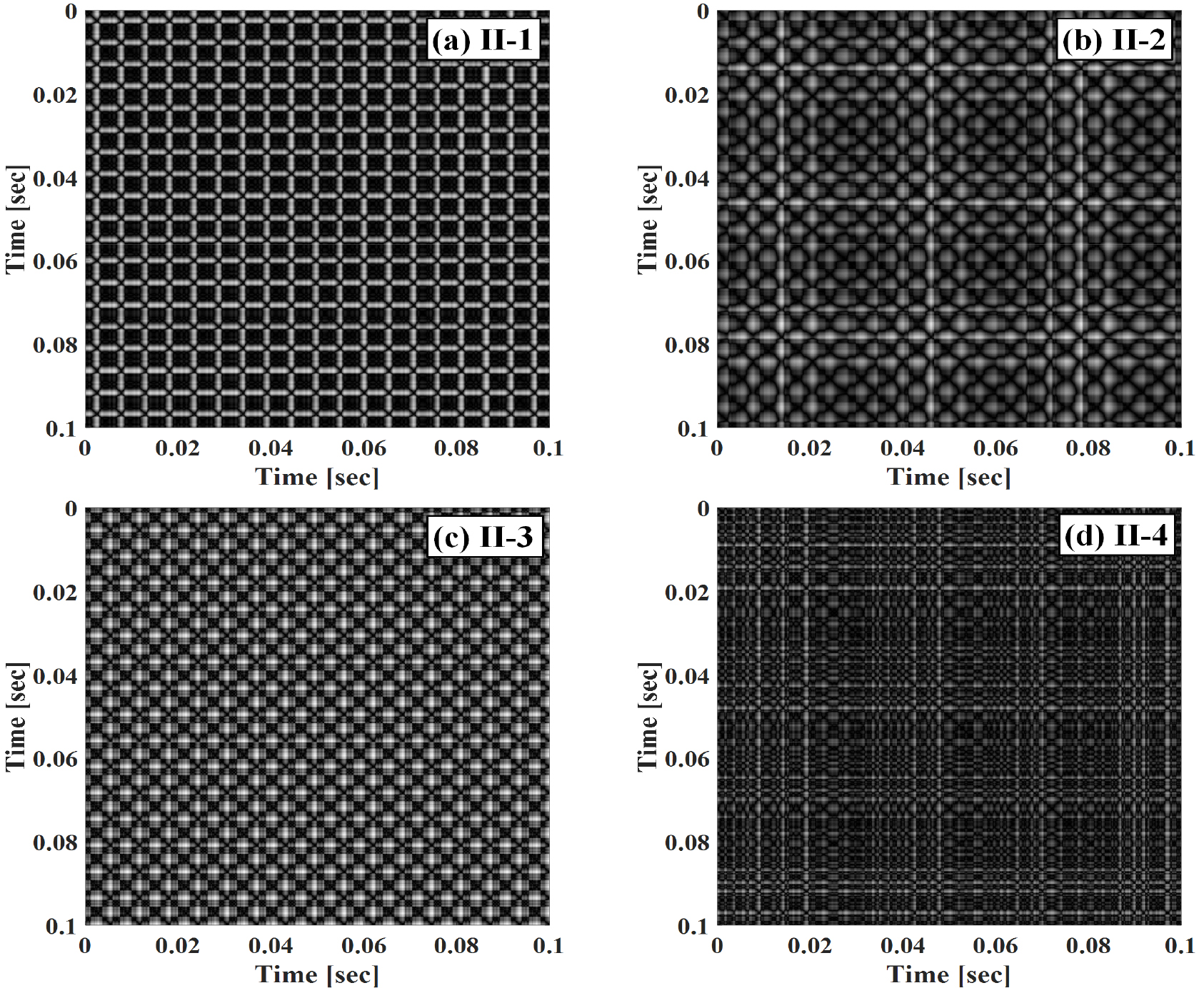
Fig. 7은 Fig. 5에서 보여 준 각 Regime별 압력섭동을 2차원으로 시각화 할 수 있는 recurrence plot 방법을 이용하여 나타내었다. recurrence plot은 특정 신호를 정사각 행렬(matrix)로 변환 후 시각화함으로써 시간에 따른 신호의 발달과정을 볼 수 있고 단시간에 취득한 데이터의 주기성을 시각적으로 쉽게 구분할 수 있는 판별법이다[25, 26, 27]. 이 경우 패턴의 반복 횟수를 고려하여 Fig. 5에서와 동일하게 0 ~ 0.1초에 해당하는 압력섭동의 데이터들을 사용하였다.

Fig. 7.

Analysis of pressure fluctuation pattern shape of representative conditions of each regime using recurrence plot method; (a) II-1(Φ = 0.55, Re_D = 1600), (b) II-2(Φ = 0.65, Re_D = 2000), (c) II-3(Φ = 0.85, Re_D = 2000), (d) II-4(Φ = 0.85, Re_D = 2500).

일반적으로 recurrence plot에 의하면 주기성이 뚜렷한 거동인 경우 일정한 패턴이 명확하게 구분되어 나타나게 되는데, 일정한 주기를 가지는 (a) II-1과 (c) II-3은 지배적인 주파수에 따라 패턴의 형상이 일정하게 명확한 형태로 분포하는 것을 볼 수 있으나 (b) II-2는 맥놀이 주파수로 인하여 작은 패턴과 큰 패턴이 같이 생성된 것을 확인할 수 있다. 그리고 (d) II-4인 경우에서는 패턴의 크기가 불규칙하고 선명하질 않게 분포되어 Fig. 6 (d) II-4의 위상 궤적도에서 보여준 바와 같이 다수의 어트랙터들이 관여된 불규칙한 거동임을 확인해 주고 있다.

이처럼 진동화염의 압력섭동 데이터를 time signal과 FFT 방법뿐만 아니라 동역학적 모드 분석법인 phase portrait와 recurrence plot 방법을 사용하여 각 Regime별로 서로 다르게 거동하고 있는 진동화염임을 알 수 있었다.

3.4 소음의 강도 및 주파수 경향

앞 절에서는 각 Regime별 다르게 나타나는 화염의 불안정성 차이를 다양한 분석법들을 통하여 살펴보았다. 그런데 이러한 기본적인 특성은 연소조건에 따라 일정한 경향을 가지는 것이 확인되었는데 본 절에서는 Fig. 2의 안정화 선도에서 나타난 당량비와 레이놀즈수에 따른 주파수와 소음의 강도가 어떤 경향을 띄고 있는지를 확인한다.

화염 부근에서 측정한 압력데이터를 이용하여 소음의 강도를 음압 레벨(sound pressure level)로 나타내었고 식(2)을 통해 구하였다.

여기서 P_s는 화염대 부근에서 측정한 압력데이터를 제곱평균제곱근(root mean square, rms)한 값이고 P_ref는 20 μPa을 사용하였는데, 이는 사람의 최소 가청치에 해당되는 음압이다. 연소조건과 각 Regime에 따른 음압레벨과 주파수 경향을 Fig. 8과 Fig. 9에 나타내었다.

Fig. 8.

Trend analysis of Sound Pressure Level and frequency with Reynolds number at fixed equivalence ratio.

Fig. 9.

Trend analysis of Sound Pressure Level and frequency with equivalence ratio at fixed Reynolds number.

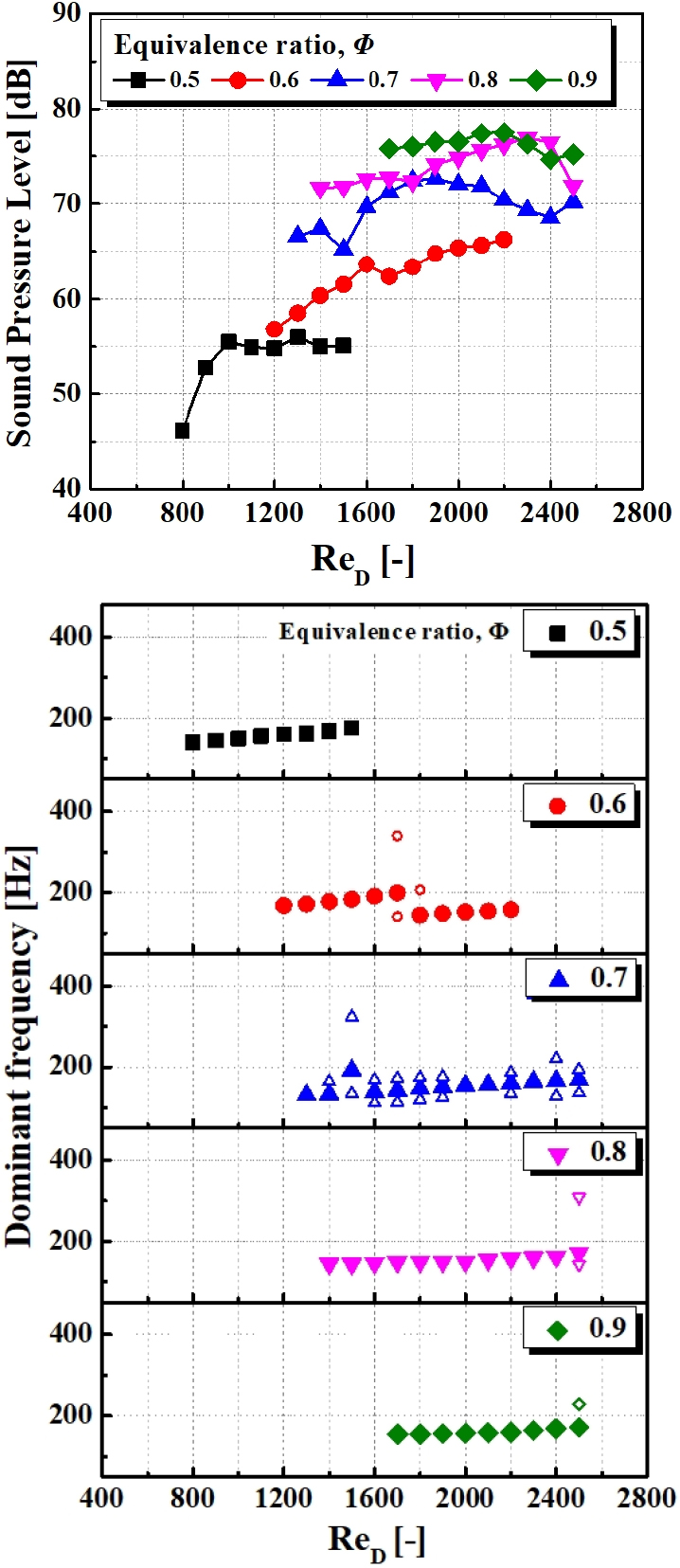
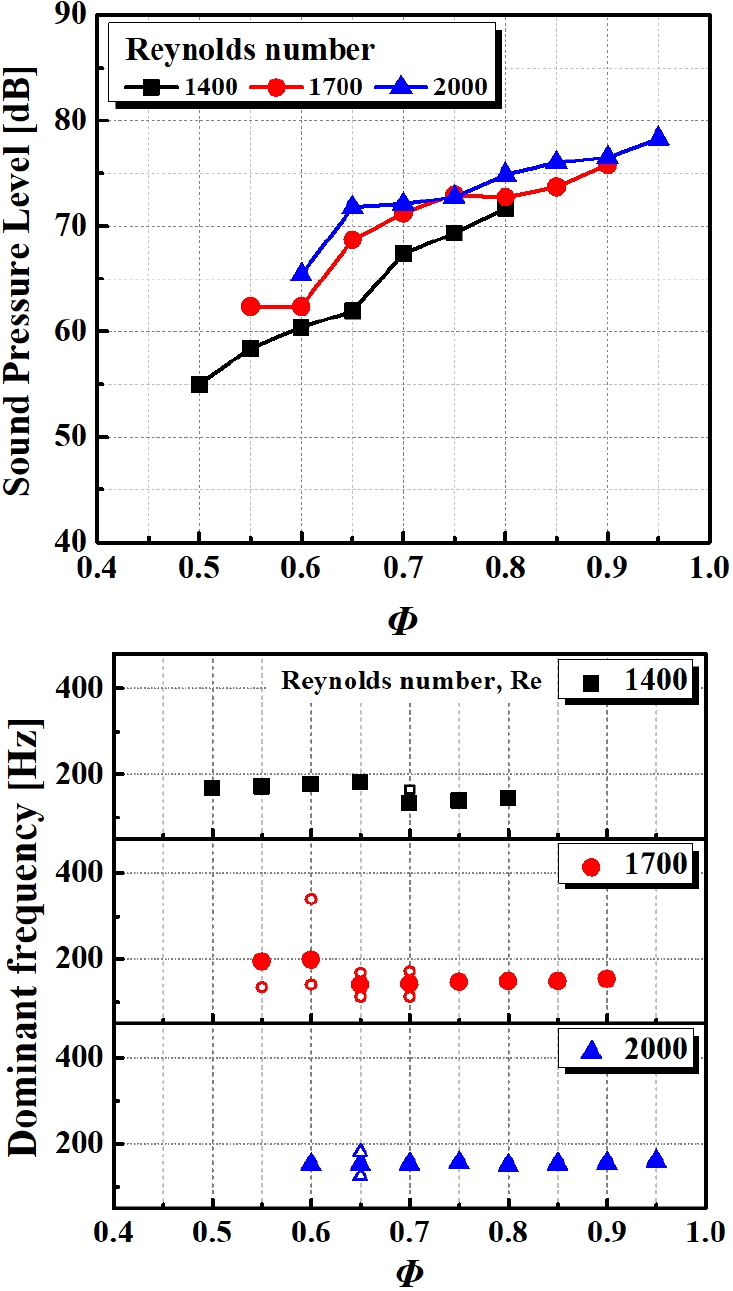
우선 Fig. 8은 레이놀즈수에 따른 당량비별 음압레벨과 주파수 경향을 보여주고 있다. 모든 당량비에서 천이영역 값을 갖는 이전에서 레이놀즈수가 증가함에 따라 발열량과 노즐 출구의 평균유속이 증가하여 음압레벨도 대체적으로 함께 증가하는 것을 볼 수 있다. 그런데 흥미로운 점은 특히 Φ = 0.6인 경우 Re_D = 1600을 지나면서 음압레벨이 감소했다가 다시 증가하는 경향을 보였다. 이는 Fig. 2의 안정화 선도에서 확인할 수 있듯이, 하나의 지배주파수로 거동하는 II-1에서 잔여주파수가 함께 존재하는 II-2로 바뀐 후에 다시 하나의 지배주파수로 거동하는 II-3으로 들어서면서 생긴 현상임을 알 수 있다. 이는 Fig. 8의 아래 그래프들 중 2번째 단인 Φ = 0.6의 그래프를 보면 더욱 명확하게 볼 수 있는데, 레이놀즈 수가 증가함에 따라 지배주파수가 199 Hz 까지 증가하다가 Re_D = 1700에서 잔여주파수가 생기기 시작한다. 그 후, Re_D = 1900 이상부터는 잔여 주파수가 다시 사라지고 지배주파수가 144.5 Hz로 급격히 작아진 상태로 다시 서서히 증가하는 것을 볼 수 있다. 이러한 현상은 3.2절에서 설명한 바와 같이 화염형상과 와류의 차이점과 같이 Regime II-1과 II-3로 나누는 기준이 된다.

그리고 모든 당량비 조건에서 천이영역에 해당되는 Re_D = 2500 근처에서는 음압레벨이 감소하는 경향을 보이고 있다. 이는 II-4 구간이 천이되는 유동의 영향을 받아 연소소음이 낮아지는 것으로 판단되며, 앞 절의 phase portrait와 recurrence plot에서 나타난 바와 같이 복수의 어트랙터로 여러 주파수가 함께 존재하게 되면서 이들 간 상쇄 작용을 일으켜 음압레벨이 다소 감소하는 것으로 판단된다.

Fig. 9는 당량비 변화에 따른 레이놀즈수 별 음압레벨과 지배적인 주파수의 경향을 나타내었다. 이 경우에도 모든 레이놀즈수 별로 당량비가 양론비(stoichiometric ratio) 근처로 증가함에 따라 연소반응이 활발하게 되어 음압레벨이 증가하는 것을 볼 수 있다. 그리고 지배주파수 증감 경향이 달라질 때, 즉 Regime II-1에서 II-3로 넘어가는 구간에서도 음압레벨이 큰 폭으로 증가하는 것을 볼 수 있다.

이처럼 Regime II-1에서 II-3 조건으로 바뀔 때에는 지배적인 주파수의 증감 경향이 달라질 뿐 만 아니라 음압 레벨에도 변화가 수반되는 것을 확인할 수 있었다. 그리고 Regime II-2 같은 경우, Regime II-1의 지배적인 주파수 또는 Regime II-3의 지배적인 주파수의 경향을 따르면서 잔여주파수가 존재하는 것을 확인할 수 있다(Fig. 8의 아래 그래프 중 2번째 단, Fig. 9의 아래 그래프 중 2번째 단). 이를 토대로 Regime II-2의 영역은 Regime II-1의 화염에서 Regime II-3의 화염으로 연소조건이 바뀔 때 나타나는 transition 구간으로 판단된다.

3.5 연소조건에 따른 주파수 민감도 분석

앞 절에서는 지배적인 주파수 하나로 거동하는 Regime II-1, II-3과 잔여주파수가 함께 존재하는 Regime II-2, II-4가 연소조건에 따라 경향성이 서로 다름을 확인하였다. 잔여주파수의 존재가 화염과 와류의 형상에는 영향을 미치고 있지만 지배적인 주파수의 경향은 그대로 유지되는 것이 확인되었으며, 전체적인 조건에서 지배주파수의 경향이 당량비와 레이놀즈수가 증가함에 따라 같이 증가하였지만 Regime II-1과 II-3에서는 서로 다른 주파수 경향을 보였다.

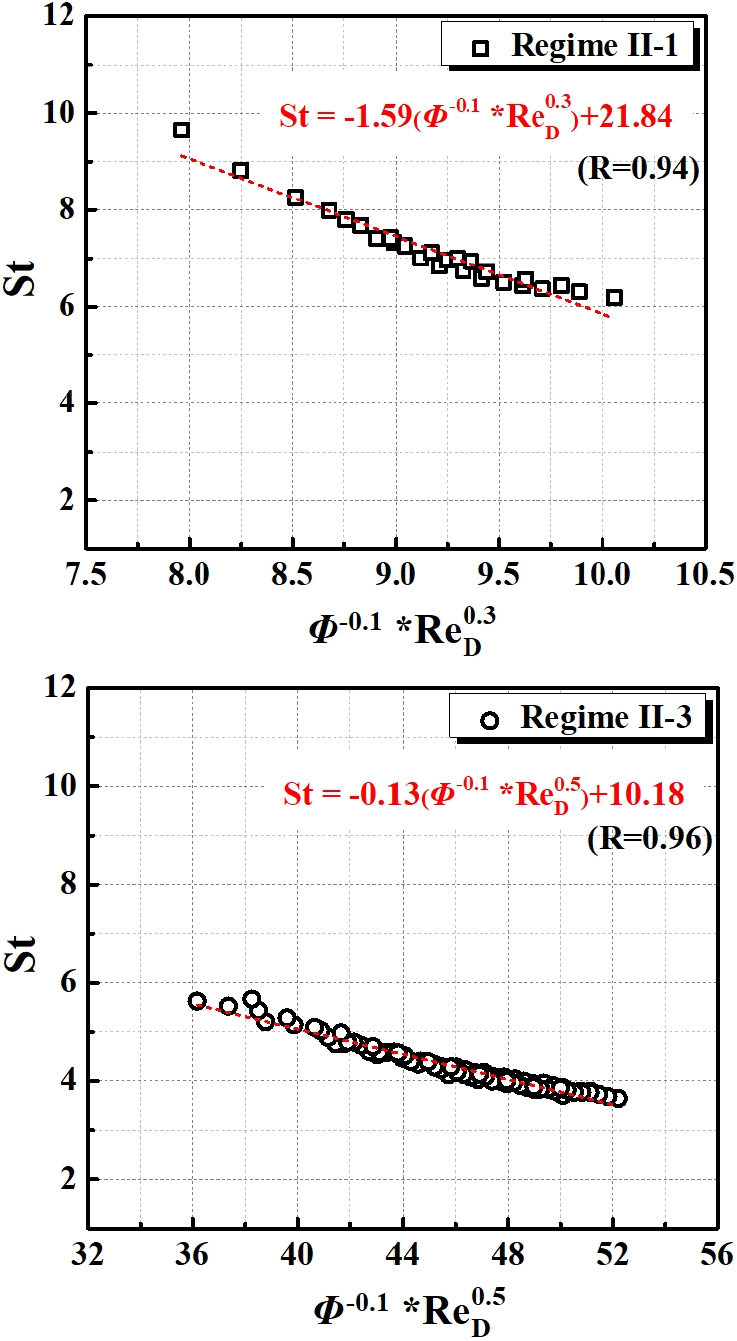
이처럼 Fig. 2에서 나타난 연소불안정 구간에서 심한 연소소음과 진동을 수반하나 주기적인 지배주파수 특성이 서로 다른 경우(Regime II-1과 Regime II-3), 연소불안정 선도(map)의 주요 매체변수인 당량비와 레이놀즈수에 따른 민감도를 분석하고자 이들 매체들과의 상관관계식으로 표현하여 Fig. 10에 나타내었다. 진동하는 화염에서 연소불안정성의 지배적인 주파수를 스트로우할 수(Strouhal number)로 표현하였고, 식 (3)을 이용하여 계산하였다.

여기서 f는 해당 조건의 지배주파수이고 D는 노즐출구의 직경으로 본 연구에서는 10 mm이며, U는 해당 조건에서 노즐출구의 평균속도이다.

Fig. 10.

Trend analysis of Sound Pressure Level and frequency with equivalence ratio at fixed Reynolds number.

Regime II-1에서 지배주파수들을 이용한 스트로우할 수는 당량비, 레이놀즈수를 이용하여 St=-1.59×(Φ-0.1×Re0.3)+21.84로 표현할 수 있었고, 일치율을 나타내는 상관계수(correlation coefficient, R)는 0.94로 잘 일치하는 것을 알 수 있다. 또한 Regime II-3의 지배적인 주파수들은 St=-1.59×(Φ-0.1×Re0.3)+21.84로 표현이 가능했으며 이 경우 상관계수는 0.96이였다. 이는 레이놀즈수와 스트로우홀 수가 비례하는 비반응 제트유동에 의해 생성된 불안정성과는 다르게 본 연구의 경우 레이놀즈수에 따라 스트로우홀 수가 감소하는 것으로 나타났다[28].

4. 결 론

본 연구는 충돌제트 화염 중 부상된 디스크 화염에서 나타난 열음향적 불안정성에 관한 연구로, 수소함량이 증가된 조성비 H₂:CO = 50:50의 예혼합 합성가스 연소시 나타난 충돌제트 화염에서 진동하는 화염의 소음(압력섭동) 특성을 분석하여 다음과 같은 결론을 얻었다.

1) 고속촬영으로 취득한 화염의 직접사진 거동과 Mie- scattering을 이용하여 취득한 유동장 이미지, 기본적인 압력섭동 특성들을 파악하여 총 4 개의 Regime으로 구분하였고, 구분된 Regime들을 안정화선도를 통해 나타내었다.

2) Regime II-1은 하나의 지배주파수와 성질이 비슷한 조화주파수로 거동하는 구간으로 균일한 화염이미지와 유동장 이미지로 확인하였다.

3) Regime II-2는 지배주파수 외에 다른 여러 주파수가 발견되었고 이를 잔여주파수라고 정의하였다. FFT 결과, 이러한 잔여주파수들은 지배적인 주파수의 양옆으로 비슷한 값을 가지고 있으며 이로 인하여 맥놀이 현상이 발생하는 구간이다. 또한 Regime II-2는 Regime II-1과 Regime II-3 사이에서 주로 발생하였으며 지배적인 주파수는 II-1 또는 II-3의 지배적인 주파수 경향과 일치하였다.

4) Regime II-3은 II-1과 비슷하게 하나의 지배주파수로 거동하였지만 phase portrait와 recurrence plot의 시각화 방법을 추가하여 II-1과는 다른 모드로 진동하는 구간임을 확인하였다. 또한 Regime II-1에서 Regime II-3으로 넘어가는 구간에서 주파수 및 소음의 세기가 달라지는 현상을 발견하였다. 이는 이전 연구서 발견되질 않아 본 연구에서 새롭게 정의된 구간으로 이전 연구에 비해 수소함량의 증가로 불안정성 모드(mode)가 바뀐 것으로 판단된다.

5) Regime II-4는 주로 Re_D > 2300에서 나타나는 영역으로 화염과 유동장, 그리고 압력섭동 데이터가 비교적 지저분한 것을 확인하였다. 이는 제트의 유동조건이 변하는 천이영역에 해당되어 발생한 현상으로 이해되었다.

6) Regime II-1과 II-3에서 다른 경향의 지배주파수 거동을 파악하기 위해 스트로우홀 수를 당량비, 레이놀즈수와의 상관관계로 특성화 한 결과, 진동연소의 소음원인이 비반응 제트유동에 의한 것보다 화염과 압력섭동으로 인하여 발생한 열음향적 불안정성이 주된 원인임을 보였다.

기호설명

f : frequency (Hz)

fd : dominant frequency (Hz)

fr : remainder frequency (Hz)

fH : resonance frequency (Hz)

Re_D : Reynolds number

St : Strouhal number

Φ : equivalence ratio

U : mixture velocity (m/s)

H : nozzle to plate distance (mm)

d : nozzle diameter (mm)

Lc : effective neck length (mm)

SPL : sound pressure level (dB)

Ps : root mean square pressure (Pa)

Pref : reference pressure (Pa)