Comparisons of Flame Stretch Calculation Models and Their Applications Part II: Model Applications

Yong Jea Kim; Minjun Choi; Kanghwan Kim; Dong-hyuk Shin

doi:10.15231/jksc.2023.28.2.038

Preview

Technical Notes

Journal of the Korean Society of Combustion. 30 June 2023. 38-56
https://doi.org/10.15231/jksc.2023.28.2.038

Comparisons of Flame Stretch Calculation Models and Their Applications Part II: Model Applications

화염 스트레치 계산 모델들의 비교와 적용 II: 모델 적용

Yong Jea Kim¹

Minjun Choi¹

Kanghwan Kim¹

Dong-hyuk Shin¹^†

김 용제¹

최 민준¹

김 강환¹

신 동혁¹^†

¹Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology

¹한국과학기술원 항공우주공학과

^{*Corresponding Author}

ABSTRACT

Model equations of the flame stretch on three dimensional stretched flame surfaces were derived by M. Matalon (1983), S. H. Chung and C. K. Law (1984), and S. M. Candel and T. J. Poinsot (1990) respectively in different forms. When applying their models into numerical and experimental data, the necessary parameters (e.g., flame location, flame migration velocity, flame speed, flow velocity, etc.) are mostly extracted on the flame surface from the data. However, their applications may not be straightforward or clear as some forms are quite complex or needs parameters outside of the flame surface. In this study, to resolve these issues, straightforward expressions were provided for one dimensional circular and spherical flame, and two dimensional steady and unsteady flames. As illustrations, the flame stretches and their constituent terms were evaluated for two dimensional steady and unsteady laminar flames.

Keywords

Flame stretch

Flame curvature

Bluff body flame

V-shape flame

MAIN

1. 서 론
2. 화염 스트레치 모델 식
2.1 화염 스트레치 산출 모델 식
2.2 화염 스트레치 산출 모델 식의 분해 표현식
2.3 화염 면 단위 법선 벡터, 화염 형상 함수, 반응 완료 영역, 비반응 영역, 및 곡률의 정의와 설정
3. 화염 면의 수치해석 및 실험 데이터 분석을 위한 화염 스트레치 모델 식의 적용
3.1 1차원 화염
3.2 2차원 화염
3.3 3차원 화염
4. 화염 스트레치 모델 식을 이용한 화염 면의 수치해석 데이터 분석 예시
4.1 2차원 정상 상태 층류 화염: 블러프 바디 화염
4.2 2차원 비정상 상태 층류 화염: 조화 진동 화염 홀더에 안정화된 V-형상 화염
5. 결 론

1. 서 론

연소실 내 연소 및 유동 현상은 화염의 형상(분포), 거동, 전파 및 이동 속도 등의 화염의 동역학적 특성들에 영향을 받는다. 연소 효율, NOx, CO 등 공해 가스 생성 등은 화염의 형상 또는 분포에 따른 연소 환경 변화에 영향을 받으며[1], 섭동하는 화염은 화염 및 유동 현상에 영향을 미쳐, 역화(flash back), 국소 소염(local extinction), 화염 날림(blow out), 연소불안정(combustion instability) 등의 발생과 연관이 있다[2,3].

화염의 형상, 거동, 이동 및 전파 등의 동역학적 특성을 연구하기 위한, 화염 면 거동의 대표적인 운동학적 특성들로는 화염 전파 속력 $s_{L}$ , 화염 면 이동 속도 ${\vec{v}}_{f}$ , 화염 면의 곡률 𝜅, 화염 스트레치 $K$ , 등이 있다. 화염의 동역학적 특성들과 연소-유동 현상의 상호영향을 연구하기 위하여[4,5,6,7], 이러한 운동학적 특성들을 명확하게 정의하고 정확하게 측정하거나 산출하여야 한다.

본 연구에서는 화염 면의 위치(형상)와 화염 면 위의 화염 및 유동 데이터(화염 전파 속력 $s_{L}$ , 화염 면 이동 속도 ${\vec{v}}_{f}$ , 등)를 이용한, 산출 모델 식을 이용한 연산이 요구되는, 화염 스트레치 $K$ 산출에 관하여 조사하였다.

화염 스트레치 개념은 B. Karlovitz[8]에 의해 처음 고려되었으며, F. A. Williams[9,10]에 의해 일반화되었다. 이동하는 미소-화염 면 요소(infinitesimal flame surface element)의 시간에 따른 변화율로 아래 식 (1)과 같이 나타난다.

(1)

K = \frac{1}{δ A} \frac{d (δ A)}{d t}

화염 면의 스트레치는 J. Buckmaster[11]에 의해 처음 고려되어 직교 좌표계(cartesian coordinate)에서의 표현식을 얻었으며, M. Matalon[12]은 이를 확장하여 일반적인 경우에 적용할 수 있는 불변 형태(invariant form)의 표현식을 구하였다. S. H. Chung and C. K. Law[13]는 화염 면에 접하는 곡선 좌표계(curvilinear coordinate)를 이용하여 화염 스트레치 표현식을 얻었다. S. M. Candel and T. J. Poinsot[14]은 플럭스 수송 정리(flux transform theorem)를 이용하여 텐서 형태의 화염 스트레치 표현식을 구하였으며 본 연구와 함께 제출한 연구, “모델 비교”[15]에서, 간략히 소개하였다.

이러한 화염 면의 스트레치 산출에 관한 대표적인 3개의 모델 식들은 서로 상이한 형태와 유도 배경을 갖고 있어 이론적 연구 목적, 수치해석 및 실험 데이터 분석 목적으로 사용할 때 혼동이 발생할 수 있다. 모델 식에 따라, 텐서 또는 벡터 연산 형태의 복잡한 표현식을 갖고 있어 실험 또는 수치해석 데이터 분석 시 적용이 용이하지 않을 수 있다. 또한, 수치해석 및 실험 데이터로부터 추출된 화염 면 정보와 화염 면 위에서 측정된 화염 및 유동 정보를 이용하여 화염 스트레치를 산출할 때, 모델 식에 따라(화염 면 밖의 정보를 요구하여) 미지수가 발생하거나 적용이 용이하지 않을 수 있다. 본 연구와 함께 제출한 연구, “모델 비교”[15]에서는 적용 시 혼동을 줄이기 위해, 화염 스트레치 산출을 위한 3개의 모델 식들의 동일함을 묘사하였다. 화염 스트레치 산출 모델 식들을 이론적 연구 목적이나 수치해석 및 실험 데이터 분석을 위한 목적으로 적용할 때, 특이점과 장단점들을 고찰하였다.

본 연구에서는, 수치해석 및 실험을 통해 얻은 화염 및 유동장 데이터를 분석하여 화염 스트레치를 산출하기 위한, 화염 스트레치 모델 식의 적용을 간략히 묘사하였다. 1차원 원형/구형 화염, 정상 상태(steady)의 2차원 화염, 비정상 상태(unsteady)의 2차원 화염의 화염 스트레치 산출을 위한 명료한 산술식들을 제공하였다. 화염 스트레치 산출 예시로 정상 상태의 2차원 층류(laminar) 블러프 바디 화염(bluff body flame)의 화염 스트레치와 비정상 상태의 조화 진동(harmonic oscillation)하는 화염 홀더(flame holder)에 안정화된 2차원 층류 V-형상 화염의 화염 스트레치를 산출하였다.

2. 화염 스트레치 모델 식

본 연구와 함께 제출한 연구, “모델 비교”[15]에서 기술하였듯이, 화염 스트레치 모델 식들을 간략히 소개하였다. 화염 스트레치 모델 식들의, 화염의 거동에 따른 분류를 이용하거나, 화염의 이동에 기여하는 인자들의 분류를 이용하여, 분해한 형태의 표현식들을 제공하였다.

2.1 화염 스트레치 산출 모델 식

화염 스트레치는, 앞서 언급한 식 (1)과 같이, 이동하는 화염 면의 미소-면 요소의 넓이의 시간 변화율을 나타낸다. 화염 스트레치 산출 모델 식들은, 국소 지점에서의 화염 스트레치를 계산하기 위해, 미소 화염 면 넓이의 시간 변화율을 직접 계산하는 대신, 화염 면의 국소 이동 속도와 화염 면의 기하학적 정보들로부터 화염 스트레치를 산출한다.

이러한 화염 스트레치 계산을 위한 3가지 모델 식들, i) Matalon[12], ii) Chung and Law[13], iii) Candel and Poinsot[14]을 아래 Table 1에 소개하였다(문헌에 나타난 모델 식들의 변수명, 연산식, 및 기호 표현들은 비교를 위해 적절히 변경하였다.).

Table 1.

Flame stretch model equations

Author	Flame stretch model equation	Additional information	Ref.
M. Matalon	$K = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} - \frac{\partial F / \partial t}{\| \nabla F \|} (\nabla \circ \vec{n})$	$F = 0, \frac{\partial F / \partial t}{\| \nabla F \|} = - {\vec{v}}_{f} \circ \vec{n}$	[12]
S. H. Chung and C. K. Law	$K = \nabla_{s} \circ {\vec{v}}_{f, τ} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$	${\vec{v}}_{f, τ} = {\vec{v}}_{f} - ({\vec{v}}_{f} \circ \vec{n}) \vec{n}$	[13]
S. M. Candel and T. J. Poinsot	$K = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f}$	$\vec{n} \vec{n} : \nabla {\vec{v}}_{f} = n_{j} \frac{\partial v_{f, i}}{\partial x_{j}} n_{i}$	[14]

3차원 공간에서 화염 면이 각 국소 지점의 화염 이동 속도로 이동할 때, 화염 면의 위치, 방향, 형상(곡률 및 면 요소의 형상)과 넓이가 변화하게 된다. 아래 Fig. 1에 기준 직교 좌표계(reference cartesian coordinate), $(x, y, z)$ ,에 대하여 국소 화염 이동 속도 ${\vec{v}}_{f}$ 로 이동하는 3차원 공간 내 화염 면을 나타내었고, 미소 화염 면을 회색으로 채색하여 나타내었다. 국소 지점에서 미소-면에 수직인 단위 법선 벡터 $\vec{n}$ 과 미소-면에 접하는 단위 직교 접선 벡터들 $\vec{τ_{1}}, \vec{τ_{2}}$ 은 미소-면에 접하는 곡선 좌표계(curvilinear coordinate), $(ξ_{1}, ξ_{2}, η)$ ,의 기저 벡터(basis vector)를 이룬다. 즉, 미소 화염 면은 국소 곡선 직교 좌표계에서 각 변의 길이 $\partial ξ_{1}$ 과 $\partial ξ_{2}$ 로 이루어진 사각형의 면 요소이다(Fig. 1의 회색으로 채색된 부분 참조). 또한, 국소 화염 이동 속도 ${\vec{v}}_{f}$ 는 화염 면에 수직인 성분 ${\vec{v}}_{f, n}$ 과 접하는 성분 ${\vec{v}}_{f, τ}$ 로 나눌 수 있다. 화염 스트레치 산출 모델 식들의 비교를 위한 변수 명의 통일을 위하여, Fig. 1에 공통으로 사용된 최소한의 변수들을 나타내었다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F1.jpg

Fig. 1.

A schematic of a flame surface and its curvilinear coordinate system and the reference coordinate system.

2.2 화염 스트레치 산출 모델 식의 분해 표현식

화염 스트레치 모델 식들은 화염의 거동에 따른 분류를 이용하거나, 화염의 이동에 기여하는 인자들의 분류를 이용하여 분해한 형태로 표현할 수 있다.

화염 스트레치 모델 식들을, 화염의 거동을 고려하여, 화염 면이 화염 면에 접하는 방향으로 이동하며(곡률은 유지한 상태로) 발생하는 접선 화염 스트레치(tangential stretch) $K_{τ}$ 와 화염 면이 화염 면의 수직 방향으로 이동하며(곡률의 변화와 함께) 발생하는 법선 화염 스트레치(normal stretch) $K_{n}$ 으로 분해하여 나타낼 수 있다. 화염 스트레치 $K$ 는 법선과 접선 화염 스트레치 , $K_{τ}$ 의 합으로 나타난다.

화염 스트레치 계산을 위한 3가지 모델 식들의 각각 화염 거동에 따른 법선 화염 스트레치 $K_{n}$ 과 접선 화염 스트레치 $K_{τ}$ 의 표현 식들을 Table 2에 나타내었다(Candel and Poinsot의 모델 식은, 다른 2 모델 식들과는 달리, 문헌의 화염 스트레치 모델 식이 법선과 접선 스트레치의 형태가 자명하게 표현되어 있지 않아 적절히 변형하였다.).

Table 2.

Flame stretch expressions in terms of tangential and normal stretches

Author	Flame stretch $K (= K_{τ} + K_{n})$
Author	Tangential stretch $K_{τ}$	Normal stretch $K_{n}$
M. Matalon	$K_{τ} = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n}$	$K_{n} = - \frac{\partial F / \partial t}{\| \nabla F \|} (\nabla \circ \vec{n}) (or, K_{n} = - \frac{\partial F / \partial t}{\| \nabla F \|} κ)$
S. H. Chung and C. K. Law	$K_{τ} = \nabla_{s} \circ {\vec{v}}_{f, τ}$	$K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n}) (or, K_{n} = ({\vec{v}}_{f} \circ \vec{n}) κ)$
S. M. Candel and T. J. Poinsot	$K_{τ} = \nabla \circ {\vec{v}}_{f, τ}$	$K_{n} = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f, n}$

• $K = K_{τ} + K_{n} κ = \nabla_{s} \circ \vec{n} (o r \nabla \circ \vec{n}) {\vec{v}}_{f, τ} = {\vec{v}}_{f} - ({\vec{v}}_{f} \circ \vec{n}) \vec{n} \frac{\partial F / \partial t}{| \nabla F |} = - {\vec{v}}_{f} \circ \vec{n}$

다른 표현 방법으로, 화염 스트레치 모델 식들을, 화염의 이동에 기여하는 인자들을 고려하여, 유동 속도에 의한 스트레치와 연소 현상에 따른 화염 전파 속력에 의한 스트레치 성분으로 분해한 형태로 표현할 수 있다. 유동의 불균일성에 의한 화염 스트레치로, 유동 속도 $\vec{u}$ 에 의해 이동됨에 따른 스트레치 성분을 스트레치 $K_{u}$ 라 정의한다(문헌에 따라 변형률(strain)이라 명명하기도 한다.). 화염이 연소에 의해 화염 면에 수직 방향으로 전파함에 따른 화염 스트레치로, 화염 전파 속력 $s_{L}$ 에 따른 스트레치 성분을 스트레치 $K_{s_{L}}$ 라 정의한다. 화염 스트레치 $K$ 는 유동과 화염 전파에 기인한 스트레치 $K_{u}$ 와 $K_{s_{L}}$ 의 합으로 나타난다.

화염 스트레치 계산을 위한 3가지 모델 식들을 유동에 의한 이동과 화염의 연소에 의한 전파의 요인에 기인한 스트레치 $K_{u}$ 와 $K_{s_{L}}$ 로 분류하여 표현한 식들을 Table 3에 나타내었다. 또한, 유동 속도에 의한 화염 스트레치 $K_{u}$ 의 경우, 앞서 언급한 접선 화염 스트레치 $K_{τ}$ 와 수직 화염 스트레치 $K_{n}$ 에 기여하는 성분으로 다시 분류할 수 있으며 이를 각각 $K_{τ, u}, K_{n, u}$ 으로 명명하여 표기하였다. 3가지 모델 식들을 유동 속도에 의한 접선, 법선 화염 스트레치 $K_{τ, u}, K_{n, u}$ 와 화염 전파 속도에 의한(법선) 화염 스트레치 $K_{s_{L}}$ 로 분류한 표현 식들도 Table 3에 나타내었다(Candel and Poinsot의 모델 식은, 다른 2 모델 식들과는 달리, 문헌의 모델 식이 수직과 접선 스트레치의 형태가 자명하게 표현되어 있지 않아 적절히 변형하였다.).

Table 3.

Flame stretch expressions in terms of flow velocity and flame propagation velocity

Author	Flame stretch $K (= K_{u} + K_{s_{L}} = K_{τ, u} + K_{n, u} + K_{s_{L}})$
	Strain (Stretch by flow velocity) $K_{u} (= K_{τ, u} + K_{n, u})$		Stretch by flame propagation $K_{s_{L}}$
	Tangential stretch by flow velocity $K_{τ, u}$	Normal stretch by flow velocity $K_{n, u}$	Normal stretch by flame propagation $K_{n, s_{L}} (= K_{s_{L}})$
M. Matalon	$K_{u} = - \nabla \times (\vec{u} \times \vec{n}) \circ \vec{n} + (\vec{u} \circ \vec{n}) (\nabla \circ \vec{n})$		$K_{s_{L}} = s_{L} (\nabla \circ \vec{n})$
	$K_{τ, u} = - \nabla \times (\vec{u} \vec{n}) \circ \vec{n}$	$K_{n, u} = (\vec{u} \circ \vec{n}) (\nabla \circ \vec{n})$	$K_{n, s_{L}} = s_{L} (\nabla \circ \vec{n})$
S. H. Chung and C. K. Law	$K_{u} = \nabla_{s} \circ {\vec{u}}_{τ} + (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$		$K_{s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
	$K_{τ, u} = \nabla_{s} \circ {\vec{u}}_{τ}$	$K_{n, u} = (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$	$K_{n, s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
S. M. Candel and T. J. Poinsot	$K_{u} = - \vec{n} \vec{n} : \nabla \vec{u} + \nabla \circ \vec{u}$		$K_{s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
	$K_{τ, u} = \nabla \circ {\vec{u}}_{τ}$	$K_{n, u} = - \vec{n} \vec{n} : \nabla \vec{u} + \nabla \circ {\vec{u}}_{n}$	$K_{n, s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$

• For Matalon’s model equation, $\frac{\partial F / \partial t}{| \nabla F |} = - {\vec{v}}_{f} \circ \vec{n}$ is applied.

• ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$

• $K = K_{u} + K_{s_{L}} K_{u} = K_{τ, u} + K_{n, u} K_{s_{L}} = K_{n, s_{L}} κ = \nabla_{s} \circ \vec{n} (or \nabla \circ \vec{n})$

2.3 화염 면 단위 법선 벡터, 화염 형상 함수, 반응 완료 영역, 비반응 영역, 및 곡률의 정의와 설정

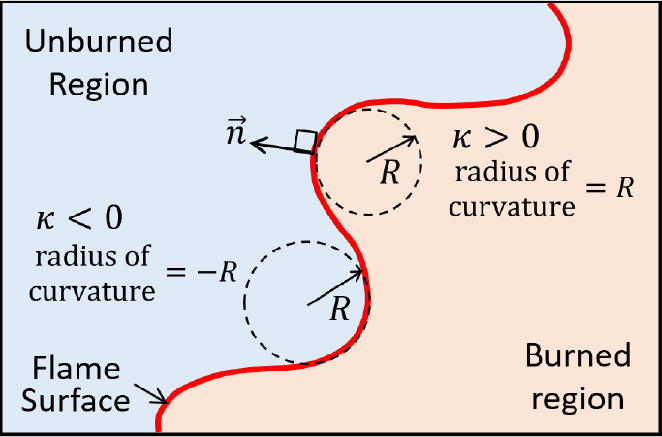
Table 1, 2, 3의 화염 스트레치 산출 모델 식들에서 사용된, 화염 면을 정의하는 화염 형상 함수 $F$ , 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ , 화염 이동 속도 ${\vec{v}}_{f}$ , 화염 전파 속력 $s_{L}$ , 곡률 𝜅(또는 곡률 반경 $R$ )의 정의는 서로 연관되어 있으며, 상호 정확한 호환이 되도록 설정되어야 한다. 본 연구와 함께 제출한 연구, “모델 비교”[15]에서 기술하였듯이, 화염 면 단위 법선 벡터 $\vec{n}$ 이 비반응 영역(unburned region)을 향하도록 하며 화염 형상 함수 $F$ 도 비반응 영역에서 양수로, 화염 면에서 0으로, 반응 완료 영역(burned region)에서 음수로 설정하는 것을 권고한다(Table 4의 Fig. (a) 참조). 곡률 𝜅와 단위 법선 벡터 $\vec{n}$ 과의 관계식 $κ = \nabla_{s} \circ \vec{n}$ 을 이용하여, 모델 식들의 $\nabla_{s} \circ \vec{n}$ 과 $\nabla \circ \vec{n}$ 을 곡률 𝜅로 치환하고[15] 곡률 반경 $R$ 을 이용하여 곡률 𝜅를 계산할 경우, 아래 Table 4의 Fig. (b)와 같이 곡률 반경을 설정하는 것을 권고한다.

Table 4.

Surface unit normal vector definition and corresponding curvature, flame shape scalar function, and flame propagation velocity

Surface unit normal vector $\vec{n}$	Flame shape scalar function $F (\nabla F = \| \nabla F \| \vec{n})$	Flame movement velocity ${\vec{v}}_{f}$	Curvature $κ (= \nabla_{s} \circ \vec{n})$
Toward unburned region	Unburned region: $F$ >0 Flame surface: $F$ =0 Burned region: $F$ <0	${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$	Convex toward unburned region: $κ > 0$ Concave toward unburned region: $κ < 0$
(a) Surface normal vector, flame shape function, flame movement velocity		(b) Curvature and radius of curvature

3. 화염 면의 수치해석 및 실험 데이터 분석을 위한 화염 스트레치 모델 식의 적용

수치해석 및 실험을 통해 얻은 화염 및 유동장 데이터를 분석하여 화염 스트레치를 산출하기 위한, 화염 스트레치 모델 식의 적용을 간략히 묘사하였다. 화염 스트레치 모델 식들은, 본 연구와 함께 제출한 연구, “모델 비교”[15]에서 기술하였듯이, 표현 형태가 다양하고 데이터에 적용이 명료하지 않거나 연산이 복잡할 수 있으므로, 이를 위한 간략화한 산출식을 제공하였다.

3.1 1차원 화염

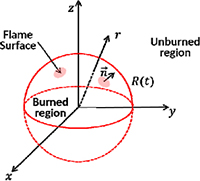
1차원 화염의 경우 평면, 원형(원통형), 또는 구형의 화염으로 화염 면의 형상과 특성치들을 하나의 좌표 변수로 표현할 수 있는 화염이다. 평면의 화염은 화염 스트레치가 일어나지 않으므로 기준점(0-스트레치 화염 특성치들, 층류 평면 화염 전파 속력 $s_{L}^{0}$ , 등)으로 삼는다. 2차원 공간 내의 원형 화염, 3차원 공간 내의 원통형 또는 구형의 화염은 크게 나누어 바깥쪽으로 전파하는 화염과 안쪽으로 전파하는 화염을 고려할 수 있으나, 후자는 실험으로 구현하기가 어려우므로 수치해석과 실험의 상호 비교보다는 이론과 수치해석으로 연구되고 있다. 본 문서에서는 원점에 반응 완료 영역(burned region)이 위치하고 바깥쪽의 비반응 영역(unburned region)을 향해 전파하는 화염의 화염 스트레치 산출 방법에 관해 간략히 논하였다(Fig. 2, 3의 1차원 원형/구형 화염 참조).

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F2.jpg

Fig. 2.

A schematic of an one dimensional outwardly propagating circular flame.

3.1.1 원형(원통형) 화염 면의 분석

화염 스트레치에 관한 연구들에서 가장 많이 사용하고 있는 문제이다. 2차원 공간 내에서 바깥쪽의 비반응 영역을 향해 전파하는 원형 화염을 Fig. 2에 나타내었다(또는 3차원 공간 내에서 전파하는 원통형 화염도 동일하게 나타낼 수 있다.). 화염 면의 위치를 원점으로부터의 거리 $R (t)$ 로 정의 및 측정하며 시간에 따른 변화를 관측하여 $\dot{R} (t)$ 를 산출한다(Fig. 2 참조).

(2)

\dot{R} (t) = \frac{d R (t)}{d t}

화염 면의 위치 $R (t)$ 이 크지 않을 경우( $R (t) < R_{c r}$ ), 원형 화염은 1차원 화염으로 가정할 수 있다(화염 면의 위치 $R (t)$ 가 화염 불안정성(flame instability)이 발생하는 $R_{c r}$ 보다 큰 경우, $R (t) > R_{c r}$ , 화염 면은 더 이상 구형이 아니며 셀 형태 등 복잡한 형태를 갖게 된다[7,16,17]. 이러한 복잡한 화염 면의 형상은 하나의 좌표 변수로 정의할 수 없으므로, 아래 소개하는 1차원 원형 화염의 화염 스트레치 산출법을 사용할 수 없으며, 일반적인 화염의 화염 스트레치 산출 방법을 따라야 한다.).

화염 이동 속도의 화염 면에 접하는 방향의 성분은 0으로 가정할 수 있으며, 화염 면의 법선 방향의 성분만 존재한다고 가정할 수 있으며, 화염 면 위치의 시간 변화율 $\dot{R} (t)$ 로 나타난다.

(3)

{\vec{v}}_{f, τ} = 0

(4)

v_{f, n} = \dot{R} (t)

따라서, Table 1, 2, 3의 모델 식들을 살펴보면 접선 스트레치 성분 $K_{τ}$ 는 0임을 알 수 있으며 법선 스트레치 성분 $K_{n}$ 만 존재하며 화염 스트레치 $K$ 에 기여함을 알 수 있다. 예를 들어 Chung and Law의 모델 식(Table 1, 2, 3 참조)을 살펴보면 접선 스트레치 성분 $K_{τ}$ 는 $K_{τ} = \nabla_{s} \circ {\vec{v}}_{f, τ}$ 로 나타나므로 위 식 (3)을 이용하면 0임을 알 수 있다.

즉, 1차원 원형 화염에서는 화염 면에 수직한 화염 이동 속도 성분과 곡률로 화염 스트레치를 산출할 수 있다. 예를 들어 Chung and Law의 모델 식(Table 1, 2, 3 참조)을 살펴보면 법선 스트레치는 $K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 과 같이 나타나며 이는 화염 면에 수직한 화염 이동 속도 성분 $v_{f, n} = {\vec{v}}_{f} \circ \vec{n}$ 과 곡률 $κ = \nabla_{s} \circ \vec{n}$ 의 곱이다.

화염 면에 수직한 화염 이동 속도 성분 $v_{f, n}$ 은 위 식 (4)와 같이 측정한 화염 면 위치의 시간 변화율 $\dot{R} (t)$ 를 이용해 구할 수 있다.

원형(원통형) 화염의 경우, 곡률을 $\nabla_{s} \circ \vec{n}$ 을 직접적으로 이용하지 않고, 곡률의 정의로부터 아래와 같이 간접적으로 구할 수 있다. 화염 면의 위치 $R (t)$ 을 곡률 반경으로 사용하여 원 또는 원통의 곡률 정의를 이용하면 아래와 같이 곡률을 구할 수 있다.

(5)

κ = \frac{1}{R (t)}

(곡률 반경을 구할 때, Table 4의 Fig. (b)의 규칙을 따라, 화염 면 단위 법선 벡터 $\vec{n}$ 과 곡률 반경의 정의들이 상호 정확한 호환이 되어 부호의 오류가 없도록 한다.)

앞서 구한 화염 면에 수직한 화염 이동 속도 성분(식 (4))과 곡률(식 (5))을 이용해 아래와 같이 법선 화염 스트레치 $K_{n}$ 를 산출할 수 있으며, 접선 화염 스트레치 $K_{τ}$ 는 0이므로 (총) 화염 스트레치 $K$ 와 같다.

(6)

K = K_{n} = \frac{v_{f, n}}{R (t)} = \frac{\dot{R} (t)}{R (t)}

식 (6)과 같이 1차원 원형 화염에서는 화염 면 위치의 시간 변화율 $\dot{R} (t)$ 만을 이용하여 화염 스트레치를 산출할 수 있다(이러한 이유로, 대부분의 연구들이 화염 스트레치 산출을 위하여 복잡한 연산의 모델 식을 이용하지 않고, 측정된 화염의 위치 $R (t)$ 를 이용한 방법을 사용한다.).

바깥쪽의 비반응 영역을 향해 전파하는 1차원 원형(원통형) 화염의 화염 스트레치의 산출을 위한 수식들을 Table 5에 나타내었다. 또한, 앞서 언급한 법선 및 접선 화염 스트레치 성분 $K_{n}, K_{τ}$ 을 이용한 분해 표현식과 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인들을 고려한 분해 표현식에 해당하는 화염 스트레치 수식들을 나타내었다.

Table 5.

Flame stretch analyses on one dimensional outwardly propagating flame

Flame stretch of 1-D outwardly propagating flame	Curvature 𝜅 $(\nabla_{s} \circ \vec{n})$	Strain (Stretch by flow velocity) $K_{u} (= K_{τ, u} + K_{n, u})$		Stretch by flame propagation $K_{s_{L}} (= K_{n, s_{L}})$	Flame stretch $K$
		Tangential stretch $K_{τ} (= K_{τ, u})$	Normal stretch $K_{n} (= K_{n, u} + K_{n, s_{L}})$
		Tangential stretch by flow velocity $K_{τ, u}$	Normal stretch by flow velocity $K_{n, u}$	Normal stretch by flame propagation $K_{n, s_{L}}$
1-D circular flame	$κ = \frac{1}{R (t)}$	$K_{u} = \frac{u_{n}}{R (t)}$		$K_{s_{L}} = \frac{s_{L}}{R (t)}$	$K = \frac{u_{n} + s_{L}}{R (t)}$ or, $(K = \frac{v_{f, n}}{R (t)} = \frac{\dot{R} (t)}{R (t)})$
		$K_{τ} = 0$	$K_{n} = \frac{u_{n} + s_{L}}{R (t)} (or, K_{n} = \frac{v_{f, n}}{R (t)} = \frac{\dot{R} (t)}{R (t)})$
		$K_{τ, u} = 0$	$K_{n, u} = \frac{u_{n}}{R (t)}$	$K_{n, s_{L}} = \frac{s_{L}}{R (t)}$
1-D spherical flame	$κ = \frac{2}{R (t)}$	$K_{u} = \frac{2 u_{n}}{R (t)}$		$K_{s_{L}} = \frac{2 s_{L}}{R (t)}$	$K = \frac{2 (u_{n} + s_{L})}{R (t)}$ or, $(K = \frac{2 v_{f, n}}{R (t)} = \frac{2 \dot{R} (t)}{R (t)})$
		$K_{τ} = 0$	$K_{n} = \frac{2 (u_{n} + s_{L})}{R (t)} (or, K_{n} = \frac{2 v_{f, n}}{R (t)} = \frac{2 \dot{R} (t)}{R (t)})$
		$K_{τ, u} = 0$	$K_{n, u} = \frac{2 u_{n}}{R (t)}$	$K_{n, s_{L}} = \frac{2 s_{L}}{R (t)}$

• ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n} v_{f, n} = u_{n} + s_{L} u_{n} = \vec{u} \circ \vec{n}$

3.1.2 구형 화염 면의 분석

3차원 공간 내에서 바깥쪽의 비반응 영역을 향해 전파하는 구형 화염의 경우도 앞서 언급한 2차원 공간 내에서 전파하는 원형 화염의 경우와 유사한 방법으로 화염 스트레치를 산출할 수 있다.

앞서 원형 화염의 경우와 유사하게, 화염 면의 위치 $R (t)$ 를 측정하여 시간에 따른 변화를 관측하여 $\dot{R} (t)$ 를 산출한다(Fig. 3 참조).

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F3.jpg

Fig. 3.

A schematic of an one dimensional outwardly propagating spherical flame.

화염 면의 위치 $R (t)$ 가 크지 않다는 조건으로 구형 화염은 1차원 화염으로 가정할 수 있다. 화염 이동 속도의 화염 면에 접하는 방향의 성분 ${\vec{v}}_{f, τ}$ 은 0으로 가정할 수 있으며, 접선 스트레치 성분 $K_{τ}$ 는 0임을 알 수 있으며 법선 스트레치 성분 $K_{n}$ 만 존재하며 화염 스트레치 $K$ 에 기여함을 알 수 있다(원형 화염과 마찬가지로, 화염 면의 위치 $R (t)$ 가 큰 경우, $R (t) > R_{c r}$ , 화염 불안정성[7,16,17]이 발생하게 되며 이러한 복잡한 화염 면의 형상은 하나의 좌표 변수로 정의할 수 없으므로, 아래 소개하는 1차원 구형 화염의 화염 스트레치 산출법을 사용할 수 없으며, 일반적인 화염의 화염 스트레치 산출 방법을 따라야 한다.).

Table 1, 2, 3의 모델 식들을 살펴보면, 구형 화염에서는 화염 면에 수직한 화염 이동 속도 성분과 곡률을 이용하여 화염 스트레치를 산출할 수 있다. 예를 들어 Chung and Law의 모델 식(Table 1, 2, 3 참조)을 살펴보면 법선 스트레치는 $K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 과 같이 나타나며, 접선 스트레치 성분 $K_{τ}$ 는 0이므로 (총) 화염 스트레치 $K$ 는 법선 스트레치 성분 $K_{n}$ 과 같다.

원형 화염의 경우와 같이 화염 면에 수직한 화염 이동 속도 성분 $v_{f, n}$ 은 위 식 (4)와 같이 측정한 화염 면 위치의 시간 변화율 $\dot{R} (t)$ 를 이용해 구할 수 있다.

원형 화염의 경우와 유사하게, 구형 화염의 곡률을 $\nabla_{s} \circ \vec{n}$ 을 직접적으로 이용하지 않고, 곡률의 정의로부터 아래와 같이 간접적으로 구할 수 있다. 화염 면의 위치 $R (t)$ 을 곡률 반경으로 사용하여 구의 곡률 정의를 이용하면 아래와 같이 곡률을 구할 수 있다(원형 화염의 곡률과는 계수가 다르다.).

(7)

κ = \frac{2}{R (t)}

앞서 구한 화염 면에 수직한 화염 이동 속도 성분(식 (4))과 곡률(식 (7))을 이용해 다음과 같이 법선 화염 스트레치 $K_{n}$ 를 산출할 수 있으며, 접선 화염 스트레치 $K_{τ}$ 는 0이므로 (총) 화염 스트레치 $K$ 와 같다.

(8)

K = K_{n} = \frac{2 v_{f, n}}{R (t)} = \frac{\dot{2 R} (t)}{R (t)}

식 (8)로부터 구형 화염에서는, 1차원 원형 화염의 경우와 같이, 화염 면 위치의 시간 변화율 $\dot{R} (t)$ 만을 이용하여 화염 스트레치를 산출할 수 있다(이러한 이유로, 대부분의 연구들이 화염 스트레치 산출을 위하여 복잡한 연산의 모델 식을 이용하지 않고, 측정된 화염의 위치 $R (t)$ 를 이용한 방법을 사용한다.).

3차원 공간 내에서 바깥쪽의 비반응 영역을 향해 전파하는 구형 화염의 화염 스트레치의 산출을 위한 수식들을 Table 5에 나타내었다. 또한, 앞서 언급한 법선 및 접선 화염 스트레치 성분 $K_{n}, K_{τ}$ 을 이용한 분해 표현식과 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인들을 고려한 분해 표현식에 해당하는 화염 스트레치 성분들을 나타내었다.

3.2 2차원 화염

2차원 화염의 경우, 화염 면의 형상과 특성치들을 2개의 좌표 변수로 표현할 수 있는 화염으로, 2차원 분젠 화염(bunsen flame), 정체 화염(stagnation point flame), 블러프 바디 화염(bluff body flame), V-형상 화염(v-shape flame), 등이 이에 포함된다.

2차원 화염은 정상 상태(steady)의 경우 화염 면의 형상이 시간에 따라 유지되어, 일반적인 비정상(unsteady) 화염에 비해, 보다 간단한 화염 스트레치 표현식을 가진다. 본 문서에서는 정상 상태의 2차원 화염과 비정상 상태의 2차원 화염으로 나누어 각각의 화염 스트레치 산출 방법에 관해 간략히 논하였다.

2차원 공간 내 화염을 Fig. 4에 나타내었다. 반응 완료 영역을 붉은색으로 나타내었으며 화염 밖의 비반응 영역을 나타내었다. 화염 면은 붉은색 곡선으로 나타내었다. 예시로, 기준 직교 좌표계 $(x, y)$ 를 이용하면, $x$ 좌표 위치에서 $h$ 로 화염 면의 위치를 나타낼 수 있다. 또한, 화염 면에 접하는 곡선 직교 좌표계 $(ξ_{1}, η)$ 를 나타내었다. $ξ_{1}$ 은 화염 면을 따르는 좌표이며 𝜂는 화염 면에 수직한 방향의 좌표이다. 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 과 화염 면에 접하는 화염 면 단위 접선 벡터 $\vec{τ_{1}}$ 을 나타내었다(일반적인 3차원 화염 면의 화염 스트레치 모델 식과의 혼동을 줄이고 호환/확장을 위하여 화염 면에 접하는 단위 접선 벡터를 $\vec{τ_{1}}$ 으로, 화염 면을 따르는 좌표를 $ξ_{1}$ 으로 설정하여, 3차원 화염 면의 접선/법선 벡터와 좌표 정의( $\vec{τ_{1}}, \vec{τ_{2}}, \vec{n}, ξ_{1}, ξ_{2}, η$ )의 일부분과 일치되도록 하였다.).

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F4.jpg

Fig. 4.

A schematic of a 2 dimensional flame.

화염 이동 속도 ${\vec{v}}_{f}$ 와 유동 속도 $\vec{u}$ 를 2차원 화염 면에 접하는 성분과 수직한 성분으로 나누어 각각 아래와 같이 정의하였다.

(9)

{\vec{v}}_{f} = {\vec{v}}_{f, n} + {\vec{v}}_{f, τ_{1}}

(10)

v_{f, n} = {\vec{v}}_{f} \circ \vec{n}

(11)

v_{f, τ_{1}} = {\vec{v}}_{f} \circ \vec{τ_{1}}

(12)

\vec{u} = {\vec{u}}_{n} + {\vec{u}}_{τ_{1}}

(13)

u_{n} = \vec{u} \circ \vec{n}

(14)

u_{τ_{1}} = \vec{u} \circ \vec{τ_{1}}

3.2.1 정상 상태 2차원 화염 면의 분석

정상 상태의 화염의 경우, 화염 면의 형상이 시간에 따라 동일하게 유지된다. 이는, 화염 면이 국소 지점에서 화염 면의 수직한 방향으로 이동하지 않음을 의미하므로, 화염 이동 속도 ${\vec{v}}_{f}$ 의 화염 면에 수직한 성분 $v_{f, n}$ 은 0이다.

(15)

v_{f, n} = {\vec{v}}_{f} \circ \vec{n} = 0

위 식 (15)를 이용하여, Table 1, 2, 3의 모델 식들을 살펴보면 법선 스트레치 성분 $K_{n}$ 은 0임을 알 수 있으며 접선 스트레치 성분 $K_{τ}$ 만 존재하며 화염 스트레치 $K$ 에 기여함을 알 수 있다. 예를 들어, Chung and Law의 모델 식(Table 1, 2, 3 참조)을 살펴보면 법선 스트레치 성분 $K_{n}$ 은 $K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 으로 나타나므로 위 식 (15)를 이용하면 $K_{n}$ =0임을 알 수 있다.

접선 스트레치 성분 $K_{τ}$ 를 구하여 (총) 화염 스트레치 $K$ 를 구하기 위해, Table 1, 2, 3의 모델 식들을 이용하여, 화염 면을 따르는 곡선 좌표 $ξ_{1}$ 을 이용하여 나타내면 아래와 같다. 유동 속도 $\vec{u}$ 를 이용한 수식과 화염 이동 속도 ${\vec{v}}_{f}$ 를 이용한 수식을 각각 식 (16), (17)로 아래와 같이 나타내었고, 명료한 적용을 위하여 간결하고 구체적인 형태로 나타내었다.

(16)

K = K_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}

(17)

K = K_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ_{1}}}{\partial ξ_{1}}

총 화염 스트레치의 산출 과정에서, 법선 스트레치 $K_{n}$ 은 0이므로, 법선 스트레치 수식에 직접적으로 포함된 곡률에 의한 영향을 정상 상태의 화염의 경우에는 고려할 필요는 없다. 그러나, 법선 스트레치는 0이나 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인에 의한 법선 스트레치들은 0이 아니다. 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인에 따른 화염 스트레치의 영향을 조사하기 위하여 곡률 계산이 필요할 수 있다. 일반적인 화염 면의 경우, 앞서 1차원 원형/구형 화염 면의 분석에서 언급한 곡률 반경의 정의를 이용하여 곡률을 구하기 용이하지 않으며, 화염 면 단위 법선 벡터 $\vec{n}$ 의 면-발산을 이용해 $κ = \nabla_{s} \circ \vec{n}$ 을 이용하여 구해야 한다[15,18]. 이를 화염 면 위의 곡선 좌표 $ξ_{1}$ 을 이용하여 명료한 적용을 위한 간결하고 구체적인 형태로 나타내면 아래와 같다.

(18)

κ = {\vec{τ}}_{1} \circ \frac{\partial \vec{n}}{\partial ξ_{1}}

유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 영향에 의한 법선 화염 스트레치 성분 , $Κ_{n, u}, Κ_{n, s_{L}}$ 를 위 식 (18)에서 구한 곡률을 이용하여 아래와 같이 구할 수 있다. 정상 상태의 화염의 경우는 화염 면이 화염 면의 수직한 방향으로 이동하지 않으므로 $v_{f, n} = u_{n} + s_{L} = 0$ 이며 $Κ_{n, u}$ 과 $Κ_{n, s_{L}}$ 의 합 $K_{n}$ 은 0이다.

(19)

Κ_{n, u} = u_{n} κ

(20)

Κ_{n, s_{L}} = s_{L} κ

2차원 공간 내에서 전파하는 정상 상태의 일반적인 화염의 화염 스트레치의 산출을 위한 수식들을 Table 6에 나타내었다. (총) 화염 스트레치 $K$ , 법선 및 접선 화염 스트레치 성분 $K_{n}, K_{τ}$ 을 이용한 분해 표현식, 그리고 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인들을 고려한 분해 표현식에 해당하는 화염 스트레치 수식들을 나타내었다.

Table 6.

Flame stretch analyses on two dimensional steady flame

Flame stretch of 2-D steady flame	Strain (Stretch by $\vec{u}$ ) $Κ_{u} (= Κ_{τ, u} + Κ_{n, u})$		Stretch by $s_{L}$ $Κ_{s_{L}} (= Κ_{n, s_{L}})$		Flame stretch $K$
	Tangential stretch $Κ_{τ} (= Κ_{τ, u})$	Normal stretch $Κ_{n} (= Κ_{n, u} + Κ_{n, s_{L}})$
	Tangential stretch by $\vec{u}$ $K_{τ, u}$	Normal stretch by $\vec{u}$ $K_{n, u}$	Normal stretch by $s_{L}$ $K_{n, s_{L}}$
Expression using the flame surface curvilinear coordinate	$Κ_{u} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}} + u_{n} κ$		$Κ_{s_{L}} = s_{L} κ$		$Κ = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}$ or, $(Κ = {\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ_{1}}}{\partial ξ_{1}})$
	$Κ_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}$ or, $(Κ_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ_{1}}}{\partial ξ_{1}})$	$Κ_{n} = 0$
	$Κ_{τ, u} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}$	$Κ_{n, u} = u_{n} κ$	$Κ_{n, s_{L}} = s_{L} k$
Straightforward expression using the coordinate $x$	$Κ_{u} = α^{5} \frac{d h}{d x} d^{2} h d x^{2} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x}) + α (\frac{d h}{d x} u_{x} - u_{y}) κ$		$Κ_{s_{L}} = s_{L} κ$		$Κ = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x})$ or, $Κ = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- v_{x} + v_{f, y}) + α^{3} (\frac{d v_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d v_{f, y}}{d x})$
	$Κ_{τ} = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- v_{f, x} + v_{f, y}) + α^{3} (\frac{d v_{f, x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d v_{f, y}}{d x})$	$Κ_{n} = 0$
	$Κ_{τ, u} = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x})$	$Κ_{n, u} = α (\frac{d h}{d x} u_{x} - u_{y}) κ$	$Κ_{n, s_{L}} = s_{L} κ$
A schematic of a 2 dimensional flame		• ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$ $v_{f, n} = u_{n} + s_{L}$ • $\vec{u} = {\vec{u}}_{n} + {\vec{u}}_{τ_{1}}$ $u_{n} = \vec{u} \circ \vec{n}$ $u_{τ_{1}} = \vec{u} \circ \vec{τ_{1}}$ • ${\vec{v}}_{f} = {\vec{v}}_{f, n} + {\vec{v}}_{f, τ_{1}}$ $v_{f, n} = {\vec{v}}_{f} \circ \vec{n}$ $v_{f, τ_{1}} = {\vec{v}}_{f} \circ \vec{τ_{1}}$		• $\vec{u} = {\vec{u}}_{x} + {\vec{u}}_{y}$ $u_{x} = \vec{u} \circ \vec{i}$ $u_{y} = \vec{u} \circ \vec{j}$ • ${\vec{v}}_{f} = {\vec{v}}_{f, x} + {\vec{v}}_{f, y}$ $v_{f, x} = {\vec{v}}_{f} \circ \vec{i}$ $v_{f, y} = {\vec{v}}_{f} \circ \vec{j}$ • $α = \frac{1}{\sqrt{1 + {(\frac{d h}{d x})}^{2}}}$		• curvature $κ = \nabla_{s} \circ \vec{n}$ $κ = {\vec{τ}}_{1} \circ \frac{\partial \vec{n}}{\partial ξ_{1}}$ $κ = \frac{\frac{d^{2} h}{d x^{2}}}{{[1 + {(\frac{d h}{d x})}^{2}]}^{\frac{3}{2}}}$

앞서 언급한, 화염 스트레치 산출식들은 화염 면 위에서의 정보들만을 이용하여 계산이 가능하도록 화염 면 위에서 정의되어 있으며 화염 면을 따르는 곡선 좌표계에서 표현되어 있다. 한편, 화염 스트레치 산출을 수치적으로 수행할 때, 화염 면을 따르는 곡선 좌표 $ξ_{1}$ 을 이용한 수식은 화염 면을 등간격 격자로 모사하였을 경우에 적용이 용이하고 정확도를 갖는다. 화염 면이 등간격 격자로 구성되지 않은 경우 정확도가 저하될 수 있다.

한편, 수치해석 결과나 실험을 통한 영상 촬영 데이터의 경우, 기준이 되는 (직교) 좌표계의 등간격 격자가 사용되거나, 밀집 격자 등의 적용으로 등간격 격자가 아니더라도 기준 좌표계에서의 등간격 격자로의 재구성(reconstruction)이 편리한 경우가 있다. 예를 들어 Fig. 4 또는 Table 6의 2차원 화염에서 (열/유동 수치해석 결과의 등간격 격자 사용 여부와 관계없이) $x$ 방향 또는 $y$ 방향의 등간격 격자의 구성은 화염 면 위에서의 등간격 격자의 재구성에 비해 용이하다.

기준 직교 좌표계에서 등간격 격자로 설정된 경우, 화염 면 위에서의 곡선 직교 좌표계에서 유도된 수식들(Table 6 참조)은 적용이 용이하지 않고 정확도가 저하될 수 있다. 그러나, 화염 스트레치 산출식은, 앞서 논의하였듯이, 화염 면 위의 좌표계에서 유도된 산출식이 화염 면을 고려하지 않은 일반 기준 직교 좌표계에서 유도된 수식에 비해 명료한 적용이 가능하며, 후자의 경우 수치해석 및 실험 데이터에 적용할 경우 산출 과정 중 미지수의 처리 문제가 발생할 수 있다. 따라서, 본 문서에서는 화염 면에 접하는 곡선 직교 좌표계에서 유도된 수식들(Table 6 참조)을 이용하여 직교 좌표계에서 사용 가능하도록 변환하여 제시하였다. 그 중, $x$ 방향의 등간격 격자에서의 적용에 적합하고 정확도를 확보할 수 있는 화염 스트레치 산출식을 Table 6에 나타내었다.

3.2.2 비정상 상태 2차원 화염 면의 분석

비정상 상태의 화염은 시간에 따라 화염 면의 형상이 계속 변화하게 된다. 정상 상태의 화염의 경우, 앞서 언급하였듯이 법선 스트레치 성분 $K_{n}$ 은 0이었으나, 비정상 상태의 화염의 경우는 0이 아니며 법선 스트레치 성분 $K_{n}$ 과 접선 스트레치 성분 $K_{τ}$ 이 모두 존재하며 화염 스트레치 $K$ 에 기여한다.

접선 스트레치 성분 $K_{τ}$ 는 정상 상태 화염의 산출 방법을 동일하게 사용할 수 있으며, 앞서 언급한 식 (16), (17)을 이용하여 구할 수 있다.

법선 스트레치 성분 $K_{n}$ 과 이를 구하는 과정에서 필요한 곡률 𝜅은 정상 상태 화염의 산출 방법과 동일하게 구할 수 있다. 곡률 𝜅는 위 식 (18)를 이용해 구할 수 있으며, 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인에 의한 법선 스트레치 성분들 $Κ_{n, u}, Κ_{n, s_{L}}$ 은 각각 식 (19), (20)과 같이 구할 수 있다. 비정상 상태의 화염의 경우 화염 면이 화염 면의 수직한 방향으로 이동하는 성분 $v_{f, n} = u_{n} + s_{L}$ 은 0이 아니며 법선 화염 스트레치 $K_{n}$ 을 화염 면 이동 속도의 화염 면에 수직한 성분 $v_{f, n}$ 를 이용해 나타내면 아래와 같다.

(21)

Κ_{n, u} = v_{f, n} κ

2차원 공간 내에서 전파하는 비정상 상태의 화염의 화염 스트레치의 산출을 위한 수식들을 Table 7에 나타내었다. (총) 화염 스트레치 $K$ , 법선 및 접선 화염 스트레치 성분 $Κ_{n}, Κ_{τ}$ 을 이용한 분해 표현식, 그리고 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ 의 요인들을 고려한 분해 표현식에 해당하는 화염 스트레치 수식들을 나타내었다.

앞서 설명한 정상 상태의 화염 면의 화염 스트레치 산출식들과 같이, 2차원 공간의 비정상 상태의 화염의 화염 스트레치 산출을 위한, 화염 면을 따르는 곡선 좌표계에서 표현된 수식들과 $x$ 방향 좌표에서 표현된 수식들을 Table 7에 나타내었다. 화염 면을 등간격 격자로 모사하였을 경우는 화염 면을 따르는 곡선 좌표계에서 표현된 수식들을 수치적 차분 방법을 적용하여 정확한 화염 스트레치를 산출할 수 있다. 또한, 수치해석 결과나 실험을 통한 영상 촬영 데이터를 분석하여 화염 스트레치를 구할 경우, 기준이 되는 직교 좌표계의 등간격 격자가 사용되는 경우가 많으며, 기준 직교 좌표계를 이용하여 표현된 수식들을 이용하여 정확한 화염 스트레치를 구할 수 있다. 본 문서에서는 $x$ 방향의 등간격 격자에서의 적용에 적합하고 정확도를 확보할 수 있는 화염 스트레치 산출식을 Table 7에 나타내었다.

Table 7.

Flame stretch analyses on two dimensional unsteady flame

Flame stretch of 2-D unsteady flame	Strain (Stretch by $\vec{u}$ ) $Κ_{u} (= Κ_{τ, u} + Κ_{n, u})$		Stretch by $s_{L}$ $Κ_{s_{L}} (= Κ_{n, s_{L}})$		Flame stretch $K$
	Tangential stretch $Κ_{τ} (= Κ_{τ, u})$	Normal stretch $Κ_{n} (= Κ_{n, u} + Κ_{n, s_{L}})$
	Tangential stretch by $\vec{u}$ $Κ_{τ, u}$	Normal stretch by $\vec{u}$ $Κ_{n, u}$	Normal stretch by $s_{L}$ $Κ_{n, s_{L}}$
Expression using the flame surface curvilinear coordinate	$Κ_{u} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}} + u_{n} κ$		$Κ_{s_{L}} = s_{L} κ$		$Κ = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}} + (u_{n} + s_{L}) κ$ or, $(Κ = {\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ_{1}}}{\partial ξ_{1}} + v_{f, n} κ)$
	$Κ_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}$ or, $(Κ_{τ} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ_{1}}}{\partial ξ_{1}})$	$Κ_{n} = (u_{n} + s_{L}) κ$ or, $(Κ_{n} = v_{f, n} κ)$
	$Κ_{τ, u} = {\vec{τ}}_{1} \circ \frac{\partial {\vec{u}}_{τ_{1}}}{\partial ξ_{1}}$	$Κ_{n, u} = u_{n} κ$	$Κ_{n, s_{L}} = s_{L} κ$
Straightforward expression using the coordinate $x$	$Κ_{u} = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x}) + α (\frac{d h}{d x} u_{x} - u_{y}) κ$		$Κ_{s_{L}} = s_{L} κ$		$Κ = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x}) + α (\frac{d h}{d x} u_{x} - u_{y}) κ + s_{L} κ$ or, $Κ = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- v_{f, x} + v_{f, y}) + α^{3} (\frac{d v_{f, x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d v_{f, y}}{d x}) + α (\frac{d h}{d x} v_{f, x} - v_{f, y}) κ$
	$Κ_{τ} = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- v_{f, x} + v_{f, y}) + α^{3} (\frac{d v_{f, x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d v_{f, y}}{d x})$	$Κ_{n} = α (\frac{d h}{d x} u_{x} - u_{y}) κ + s_{L} κ$ or, $Κ_{n} = α (\frac{d h}{d x} {v_{f,}}_{x} - v_{f, y}) κ$
	$Κ_{τ, u} = α^{5} \frac{d h}{d x} \frac{d^{2} h}{d x^{2}} (- u_{x} + u_{y}) + α^{3} (\frac{d u_{x}}{d x} + {(\frac{d h}{d x})}^{2} \frac{d u_{y}}{d x})$	$Κ_{n, u} = α (\frac{d h}{d x} u_{x} - u_{y}) κ$	$Κ_{n, s_{L}} = s_{L} κ$
A schematic of a 2 dimensional flame.		• ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$ $v_{f, n} = u_{n} + s_{L}$ • $\vec{u} = {\vec{u}}_{n} + {\vec{u}}_{τ_{1}}$ $u_{n} = \vec{u} \circ \vec{n}$ $u_{τ_{1}} = \vec{u} \circ \vec{τ_{1}}$ • ${\vec{v}}_{f} = {\vec{v}}_{f, n} + {\vec{v}}_{f, τ_{1}}$ $v_{f, n} = {\vec{v}}_{f} \circ \vec{n}$ $v_{f, τ_{1}} = {\vec{v}}_{f} \circ \vec{τ_{1}}$		• $\vec{u} = {\vec{u}}_{x} + {\vec{u}}_{y}$ $u_{x} = \vec{u} \circ \vec{i}$ $u_{y} = \vec{u} \circ \vec{j}$ • ${\vec{v}}_{f} = {\vec{v}}_{f, x} + {\vec{v}}_{f, y}$ $v_{f, x} = {\vec{v}}_{f} \circ \vec{i}$ $v_{f, y} = {\vec{v}}_{f} \circ \vec{j}$ • $α = \frac{1}{\sqrt{1 + {(\frac{d h}{d x})}^{2}}}$		• curvature $κ = \nabla_{s} \circ \vec{n}$ $κ = {\vec{τ}}_{1} \circ \frac{\partial \vec{n}}{\partial ξ_{1}}$ $κ = \frac{\frac{d^{2} h}{d x^{2}}}{{[1 + {(\frac{d h}{d x})}^{2}]}^{\frac{3}{2}}}$

3.3 3차원 화염

3차원 화염의 경우, 3차원 공간에서 전파하는 화염으로, 화염 면의 형상과 특성치들을 3개의 좌표 변수로 표현할 수 있는 화염이다(화염 면을 따르는 곡선 좌표로 매개화하였을 경우는 화염 면의 형상과 특성치들을 2개의 매개 변수(parametrized variable)로 표현이 가능하다.).

3차원 화염의 경우에도, 정상 상태(steady)의 경우 화염 면의 형상이 시간에 따라 동일하게 유지되어 화염 이동 속도 ${\vec{v}}_{f}$ 의 화염 면에 수직한 성분 $v_{f, n}$ 은 0이고 법선 스트레치 성분 $K_{n}$ 은 0이며, 접선 스트레치 성분 $K_{τ}$ 만 존재하며 화염 스트레치 $K$ 에 기여한다. 비정상 상태(unsteady)의 화염의 경우 법선 및 접선 스트레치 $Κ_{n}, Κ_{τ}$ 모두 존재하며 화염 스트레치 $K$ 에 기여한다.

3차원 화염의 경우, 화염 스트레치를 구하기 위하여 Table 1, 2, 3의 모델 식들을 사용할 수 있다. 수치해석 데이터 또는 실험을 통한 영상 데이터를 사용해 화염 스트레치를 구할 경우, 명료한 적용이 가능한 Chung and Law의 모델 식을 사용할 수 있다. 그러나, 이 모델 식은 화염 면을 따르는 직교하는 곡선 좌표계를 요구하는데, 이를 위해 굴곡이 있는 3차원 화염 면을 곡선 직교 격자계로 모사하는 것이 필요하다. 화염 면 위의 격자계가 직교하지 않을 경우 정확도가 저하될 수 있다. Matalon과 Candel and Poinsot의 모델 식들을 이용할 경우, 기준 좌표계를 사용하므로 굴곡된 화염 면의 형상의 영향을 받지 않는다. 그러나, 앞서 언급하였듯이 화염 데이터가 화염 면 위에서만 주어지는 경우가 많으며, 이 경우 산출 과정 중 미지수의 처리 문제가 발생하는 등 적용이 용이하지 않을 수 있다. 따라서, Chung and Law의 모델 식이 적용이 명료하므로 사용이 보다 용이할 것으로 예상하며, 굴곡진 화염 면을 격자 재구성(grid reconstruction)을 통해, 화염 면 위의 직교하는 기저 벡터 설정을 가능하게 하거나 향상시켜 정확도를 확보하는 것이 중요할 것으로 예상된다. 1차원 및 2차원 화염의 화염 스트레치 산출의 경우에서와 같은 명료한 적용을 위한 간결한 산술식은 제공하지 않았다.

4. 화염 스트레치 모델 식을 이용한 화염 면의 수치해석 데이터 분석 예시

앞서 화염 스트레치 모델 식들(Table 1, 2, 3)을 소개하였고, 이론적 연구 목적과 수치해석/실험 데이터 분석 목적으로 각 모델을 적용할 때 장단점과 문제점을 기술하였다. 또한, 수치해석/실험 데이터를 분석하여 명료한 화염 스트레치 산출을 위한 구체적인 형태의 산술식(Table 5, 6, 7)을 제공하였다. 이를 이용하여 2차원 화염에서의 화염 스트레치 산출 예시들을 제공하였다. 2차원 정상 상태(steady) 화염의 예시로 2차원 층류(laminar) 블러프 바디 화염(bluff body flame)의 화염 스트레치를 산출하였다. 2차원 비정상 상태(unsteady) 화염의 예시로 조화 진동하는 화염 홀더(flame holder)에 안정화된 2차원 층류(laminar) V-형상 화염(V-shape flame)의 화염 스트레치를 산출하였다.

4.1 2차원 정상 상태 층류 화염: 블러프 바디 화염

2차원 정상 상태(steady) 화염의 화염 스트레치 산출 예시를 위하여, 2차원 층류(laminar) 블러프 바디 화염(bluff body flame)의 수치해석 데이터를 이용하였다. 아래 Fig. 5(a)와 같이, 당량비(equivalence ratio) 0.6의 수소/공기(H₂/Air) 예혼합 기체(premixed gas)가 4.5 m/s로 아래에서 유입되며, 가운데 위치한 3 mm 두께의 정사각형 형태의 블러프 바디에 의해 화염이 안정화된다. 층류 조건과 정상 상태 조건을 가정하였다.

수치해석을 수행하기 위하여 상용 소프트웨어 OpenFOAM의 reactingFOAM을 이용하였다[19]. 수치해석 결과들 중 온도와 유동 속도 벡터들의 방향을 아래 Fig. 5(b)에 나타내었다.

화염 및 유동장 수치해석 결과를 분석하여 아래 식 (22)와 같은 반응 진행 변수(progress variable)를 이용하여 $c$ =0.1의 등고선(iso contour)으로 화염 면을 가정하였다.

(22)

c = 1 - \frac{Y_{H_{2}} - Y_{H_{2}, b u r n e d}}{Y_{H_{2}, u n b u r n e d} - Y_{H_{2}, b u r n e d}}

반응 진행 변수 $c$ =0.1의 등고선을 이용하여 추출한 화염의 오른쪽 부분의 화염 면(Fig. 5(b) 참조)의 위치를 반응 영역과 비반응 영역의 표기와 함께 Fig. 6(a)에 나타내었다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F5.jpg

Fig. 5.

(a) A schematic of a 2 dimensional laminar bluff body flame and (b) temperature and flow direction of numerical simulation result.

화염 면 위치에서 화염 및 유동의 특성치들(밀도, 온도, 유동 속도, 등)을 수치해석 데이터로부터 추출하였다. 한편, Table 1, 2, 3의 모델 식들을 살펴보면, 화염 스트레치를 산출하기 위해서 화염 이동 속도 ${\vec{v}}_{f}$ (또는, 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ ) 정보가 필요하다. 그러나, 이러한 특성치들은 화염 및 유동장 데이터로부터 바로 추출할 수 없으며, 시간에 따른 화염 면을 추적하여 화염 이동 속도 ${\vec{v}}_{f}$ 를 산출하거나, 화염 면과 특성치들의 관계를 이용하여 화염 전파 속력 $s_{L}$ 과 유동 속도 $\vec{u}$ 를 계산해야 한다(Table 1, 2, 3 모델 식들에 사용된 유동 속도 $\vec{u}$ 는 비반응 영역의 유동 속도[15]이며, 화염 면 위치에서 추출된 유동 속도는 반응 진행 변수 $c$ =0.1 위치에서의 유동 속도이다.). 본 연구에서는 반응 진행 변수 $c$ =0.1로 가정한 화염 면 위치에서 화염 및 유동의 특성치들(밀도, 유동 속도)과 화염 면의 형상을 이용하여 화염 면에서의 화염 전파 속력 $s_{L}$ 을 구하였다(화염 면 위에서의 화염 이동 속도 ${\vec{v}}_{f}$ 또는 유동 속도 $\vec{u}$ 도 이 과정에서 함께 구해진다.). 화염 전파 속력을 산출하는 방법은 다양한 연구가 진행되고 있으며[20,21] 본 문서에서는 생략하였다. 화염 면에서의 화염 전파 속력 $s_{L}$ 을 (기준 좌표계의) $x$ 좌표를 따라 나타내면 아래 Fig. 6(b)와 같이 나타난다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F6.jpg

Fig. 6.

(a) Flame surface location, (b) flame propagation speed, (c) flame stretch, normal stretch and tangential stretch, and (d) flame stretch, stretch by flow velocity, and stretch by flame propagation speed, of the 2 dimensional laminar bluff body flame.

앞서 언급한 바와 같이, 정상 상태 화염의 경우, 화염 면의 형상이 시간에 따라 동일하게 유지되며, 화염 이동 속도의 화염 면에 수직한 성분 $v_{f, n}$ 은 0이며, 법선 스트레치 성분 $K_{n}$ 또한 0이다. 따라서, (총) 화염 스트레치 $K$ 는 접선 스트레치 $K_{τ}$ 와 법선 스트레치 $K_{n}$ 의 합이므로, 접선 스트레치 성분 $K_{τ}$ 를 구하여 (총) 화염 스트레치 $K$ 를 구할 수 있다.

Table 1, 2, 3의 모델 식들을 살펴보면 접선 스트레치 성분 $K_{τ}$ 는 화염 이동 속도 ${\vec{v}}_{f}$ 의 화염 면에 접하는 성분을 이용하여 구할 수 있다. 한편, 화염 이동 속도 ${\vec{v}}_{f}$ , 유동 속도 $\vec{u}$ , 화염 전파 속력 $s_{L}$ 은 ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$ 의 관계를 갖으므로, 화염 면에 접하는 방향의 화염 이동 속도 성분 ${\vec{v}}_{f, τ_{1}}$ 과 유동 속도 성분 ${\vec{u}}_{τ_{1}}$ 은 동일하다( $v_{f, τ_{1}} = u_{τ_{1}}$ ). 따라서, 화염 전파 속력 $s_{L}$ 과 화염 면의 이동 속도 ${\vec{v}}_{f}$ 의 산출 없이, 접선 화염 스트레치 $K_{τ}$ 를 화염 면에 접하는 유동 속도 성분 $u_{τ_{1}}$ 만을 이용하여 산출할 수 있으며, (총) 화염 스트레치 $K$ 를 산출할 수 있다.

본 문서에서 수치해석을 수행하기 위하여 기준 좌표계 $x, y$ 방향으로 정렬된 격자를 사용하였고 화염 주변에 격자가 밀집되도록 하였다. 이에 따라, 수치해석 데이터를 분석할 때 기준 좌표계 $x$ 또는 $y$ 방향으로 등간격 격자를 구성하여 각 격자점 위치의 특성치들을 산출하는 것이 편리하다. 본 문서에서는 $x$ 좌표 방향으로 등간격인 격자 계를 설정하여 화염 면의 위치와 화염 면에서의 특성치들을 구하였다.

화염 면의 형상 및 위치, 화염 면 위에서의 유동 속도 $\vec{u}$ 를 이용하여, Table 6의 $x$ 방향의 등간격 격자에서 표현된 산출식들에 적용하였다. 산출식들은 중앙 차분법(central difference)을 적용하여 수치적으로 계산하였다. 접선 화염 스트레치 $K_{τ}$ 를 구하여 (총) 화염 스트레치 $K$ 를 산출하였으며, Fig. 6(c)에 나타내었다. 또한, Table 6에 나타난 법선 및 접선 화염 스트레치 성분 $Κ_{n}, Κ_{τ}$ 을 (총) 화염 스트레치 $K$ 와 함께 나타내었다.

Fig. 6(c)를 살펴보면, 회색으로 나타난 (총) 화염 스트레치 $K$ 와 청색으로 나타난 접선 화염 스트레치 $K_{τ}$ 는 일치하며, 적색 선으로 나타난 법선 화염 스트레치 $K_{n}$ 은 0임을 알 수 있다. 이는 앞서 언급하였듯이, 정상 상태 화염은 시간에 따라 동일하게 유지되는 화염 면을 가지므로 법선 스트레치 성분 $K_{n}$ 은 0이며, 접선 스트레치 성분 $K_{τ}$ 만이 (총) 화염 스트레치 $K$ 에 기여함에 기인한다.

또한, Table 6의 산출 수식들을 이용하여 유동 속도 $\vec{u}$ 의 요인에 의한 화염 스트레치 성분과 화염 전파 속력 $s_{L}$ 의 요인에 의한 화염 스트레치 성분을 (총) 화염 스트레치 $K$ 와 함께 Fig. 6(d)에 나타내었다.

청색 선으로 나타난 유동 속도 $\vec{u}$ 에 의한 화염 스트레치 성분은 흑색 선으로 나타난 (총) 화염 스트레치 $K$ 의 거동과 유사한 형태를 보이며, (총) 화염 스트레치 $K$ 의 대부분을 기여한다. 적색 선으로 나타난 화염 전파 속력 $s_{L}$ 에 의한 화염 스트레치 성분은 유동 속도 $\vec{u}$ 에 의한 화염 스트레치 성분에 비해 작은 크기이며 총 화염 스트레치 $K$ 에 대한 기여량도 작다. 많은 연구들에서 이러한 요인들에 의한 화염 스트레치 성분들을 고려하고 있다(본 문서에서는 예시의 목적을 벗어나므로 자세한 분석과 논의는 생략한다.).

4.2 2차원 비정상 상태 층류 화염: 조화 진동 화염 홀더에 안정화된 V-형상 화염

2차원 비정상 상태(unsteady) 화염의 화염 스트레치 산출 예시를 위하여, 조화 진동(harmonic oscillation)하는 화염 홀더(flame holder)에 의해 가진되어 섭동하는 2차원 층류(laminar) V-형상 화염(V-shape flame)의 화염 스트레치를 계산하였다. 실험적 연구를 위하여 구현된 섭동하는 V-형상 화염의 예시를 Fig. 7(a)에 나타내었다[3].

수치해석을 수행하기 위하여 아래 Fig. 7(b)와 같이 설정하였다. 메탄(methane)과 수소(hydrogen)의 부피비(volume ratio) 10:3의 혼합 연료를 사용하며 공기(Air)와 당량비 1의 비율로 혼합하였다. 즉, 수소/메탄/공기(H₂/CH₄/Air) 예혼합 기체(premixed gas)가 아래에서 5 m/s로 유입되고 화염이 형성되어 화염 홀더(flame holder)에 안정화된다. 화염 홀더는 주파수 $f$ (1250 Hz)로 좌우 방향으로 조화 진동(harmonic oscillation)하며 섭동하는 V-형상의 화염(V-shape flame)이 형성된다. 층류 조건을 가정하였다.

위 Fig. 7(b)에서 나타난 바와 같이, 단위 법선 벡터 $\vec{n}$ , 곡률 𝜅, 반응 완료 영역, 비반응 영역 등의 정의들이 상호 정확한 호환이 되도록 앞서 언급한 정의 규칙 Table 4를 따라 설정하였다.

수치해석을 수행하기 위하여 직접 수치 해석 기법(Direct Numerical Simulation)을 사용하여 오픈 소스 코드인 PeleLM[22,23]을 이용하였다. 화학 반응 모델로 DRM 모델[24]을 사용하였다. 수치해석 결과들 중 온도와 유동 속도 벡터들의 방향을 Fig. 7(c)에 나타내었다.

본 문서에서 수치해석을 수행하기 위하여 기준 좌표계 $x, y$ 방향(Fig. 7(b) 참조)으로 정렬된 격자를 사용하였고, 적응 격자 기법(adaptive grid)을 사용하여 수치해석이 수행됨에 따라 화염 주변에 격자가 밀집되도록 하였다. 시간에 따라 변화하는 화염 면을 분석하기 위하여 화염 면 위의 국소 좌표계를 사용하는 대신, Fig. 7(b)에 나타난 바와 같이 고정된 좌표계 $(X, Y)$ 를 설정하여 화염 스트레치를 산출하였다. 수치해석 결과로부터 추출된 화염과 유동장의 특성치들을 좌표계 $(X, Y)$ 를 이용하여 좌표 변환(coordinate transform)하였다. 좌표계 $X$ 에 따른 화염 면의 위치가 음함수(implicit function)가 발생하지 않도록 하여, 좌표 $X$ 에 관한 미분 등의 연산이 원활하게 수행되도록 하였다.

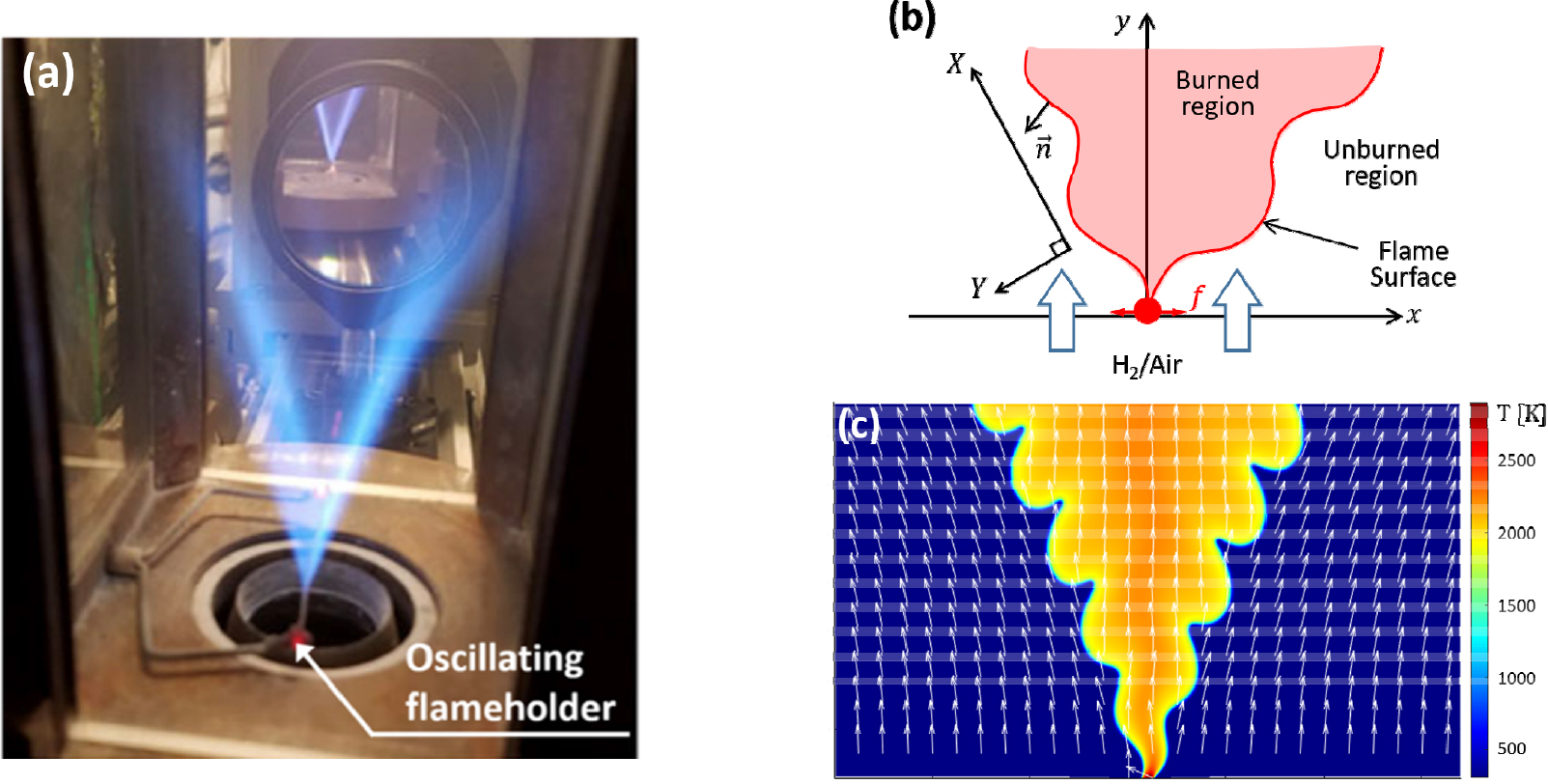
https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F7.jpg

Fig. 7.

(a) An experimental example [3], (b) a schematic of a 2 dimensional laminar fluctuating V-shape flame induced by an oscillating flame holder, and (c) temperature and flow direction of numerical simulation result.

온도 데이터를 분석하여 1177 K의 등온선을 추출하여 화염 면으로 가정하였다. 1177 K의 등온선을 이용하여 추출한 V-형상 화염의 왼쪽 부분의 화염 면(Fig. 7(c) 참조)의 위치를 좌표계 $(X, Y)$ 에 대하여 반응 영역과 비반응 영역의 표기와 함께 Fig. 8(a)에 나타내었다.

추출된 화염 면의 형상 및 위치 정보를 이용하여 곡률을 산출하여 Fig. 8(b)에 나타내었다. Table 7의 $X$ 방향의 등간격 격자에서 표현된 곡률 산출식에 적용하였으며, 중앙 차분법(central difference)을 적용하여 수치적으로 계산하였다.

추출된 화염 면 위치에서 화염 및 유동의 특성치들(밀도, 유동 속도, 등)을 수치해석 데이터로부터 추출하였다. 앞서 언급한 정상 상태의 화염 스트레치 산출의 경우와 유사하게, 수치해석 데이터로부터 추출된 $T = 1177 K$ 위치의 특성치들을 이용하여 화염 스트레치 모델식에 필요한 파라미터들(화염 이동 속도 ${\vec{v}}_{f}$ , 또는, (비반응 영역의) 유동 속도 $\vec{u}$ 와 화염 전파 속력 $s_{L}$ )의 산출이 필요하다. 본 연구에서는 추출된 밀도, 유동 속도와 화염 면의 형상을 이용하여 화염 면에서의 화염 전파 속력을 구하였다(화염 전파 속력 및 화염 이동 속도와 (비반응 영역의) 유동 속도 들을 산출하는 방법은 다양한 연구가 진행되고 있으며[20,21] 본 문서에서는 생략하였다.). 화염 면에서의 화염 전파 속력 $s_{L}$ 을 좌표계 $X$ 를 따라 나타내면 Fig. 8(c)와 같이 나타난다.

앞서 언급한 정상 상태의 화염의 경우와는 달리, 비정상 화염의 경우에는 화염 면의 형상이 시간에 따라 변화하게 되므로, 화염 이동 속도의 화염 면에 수직한 성분 $v_{f, n}$ 은 0이 아니며, 법선 스트레치 성분 $K_{n}$ 또한 0이 아니다. 따라서, 법선 스트레치 성분 $K_{n}$ 과 접선 스트레치 성분 $K_{τ}$ 를 모두 산출하여야 (총) 화염 스트레치 $K$ 를 구할 수 있다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280204/images/ksssf_28_02_04_F8.jpg

Fig. 8.

(a) An instantaneous flame surface location, (b) curvature of the flame surface, (c) flame propagation speed, (d) flame stretch, (e) flame stretch, normal stretch and tangential stretch, and (f) flame stretch, stretch by flow velocity, and stretch by flame propagation speed, of the 2 dimensional laminar fluctuating V-shape flame.

화염 면의 형상 및 위치, 화염 면 위에서의 유동 속도 $\vec{u}$ , 화염 전파 속력 $s_{L}$ (Fig. 8(c)), 화염 면 곡률 𝜅(Fig. 8(b))를 이용하여, 화염 스트레치 $K$ 를 산출하였다. Table 7을 이용하여 $X$ 방향의 등간격 격자에서 표현된 화염 스트레치 산출식들에 적용하였다. 산출식들은 중앙 차분법(central difference)을 적용하여 수치적으로 계산하였다. (총) 화염 스트레치 $K$ 를 Fig. 8(d)에 나타내었다.

Table 7의 산출 수식들을 이용하여 법선 및 접선 화염 스트레치 성분 $Κ_{n}, Κ_{τ}$ 을 산출하여 (총) 화염 스트레치 $K$ 와 함께 Fig. 8(e)에 나타내었다.

청색 선으로 나타난 접선 화염 스트레치 $K_{τ}$ 와 적색 선으로 나타난 법선 화염 스트레치 $K_{n}$ 은 섭동하는 화염 면을 따라 복잡한 형상을 가진다. 접선 화염 스트레치 $K_{τ}$ 가 증가하며 양수일 때 법선 화염 스트레치 $K_{n}$ 는 감소하며 음수인 모습을 보이는 등 서로 반대되는 거동을 보인다. 두 화염 스트레치 성분의 합인 (총) 화염 스트레치 $K$ 는 접선 화염 스트레치 $K_{τ}$ 과 법선 화염 스트레치 $K_{n}$ 의 거동보다는 다소 단순한 형태를 보인다. 앞서 언급했던, 접선 화염 스트레치 $K_{τ}$ 가 존재하지 않는 1차원 원형/구형 화염이나, 법선 화염 스트레치 $K_{n}$ 이 존재하지 않는 2차원 정상 상태 화염 들의 경우와는 달리, 법선 및 접선 화염 스트레치들 $Κ_{n}, Κ_{τ}$ 의 다양한 거동을 관측할 수 있으며 화염의 동역학적 특성을 연구하기 위해서는 이들의 분석은 중요하다(본 문서에서는 예시의 목적을 벗어나므로 자세한 분석과 논의는 생략한다.).

또한, Table 7의 산출 수식들을 이용하여 유동 속도 $\vec{u}$ 의 요인에 의한 화염 스트레치 성분과 화염 전파 속력 $s_{L}$ 의 요인에 의한 화염 스트레치 성분을 (총) 화염 스트레치 $K$ 와 함께 Fig. 8(f)에 나타내었다.

청색 선으로 나타난 유동 속도 $\vec{u}$ 의 요인에 의한 화염 스트레치 성분과 화염 전파 속력 $s_{L}$ 의 요인에 의한 화염 스트레치 성분은 두 화염 스트레치 성분의 합인 (총) 화염 스트레치 $K$ 의 거동과 유사한 형태를 보인다. 또한, 화염 전파 속력 $s_{L}$ 의 요인에 의한 화염 스트레치는 (총) 화염 스트레치의 음의 곡률 부분에서의 거동과 유사한 거동을 보이며, (총) 화염 스트레치의 양의 곡률 부분에서의 거동의 특징은 보이지 않는다. 그에 반해, 유동 속도 $\vec{u}$ 의 요인에 의한 화염 스트레치 성분은 (총) 화염 스트레치의 거동의 특징과 전반적으로 유사한 특징을 갖는다. 많은 연구들에서 이러한 요인들에 의한 화염 스트레치를 고려하고 있다(본 문서에서는 예시의 목적을 벗어나므로 자세한 분석과 논의는 생략한다.).

5. 결 론

화염의 형상 및 분포, 거동, 전파 및 이동 속도 등의 화염의 동역학적 특성들은 연소실 내 연소 및 유동 현상에 영향을 미치며, 연소 효율, NOx, CO, 등 공해 가스 생성에 영향을 미칠 뿐 아니라, 섭동하는 화염의 특성들은 역화(flash back), 국소 소염(local extinction), 화염 날림(blow out), 연소 불안정(combustion instability) 등의 현상들과 연관이 있다.

이러한 동역학적 특성을 연구하기 위한 대표적인 특성치들(characteristics)로는 화염 면의 형상/위치, 화염 전파 속력, $s_{L}$ , 화염 스트레치, $K$ , 화염 면의 곡률, 𝜅, 등이 있으며, 연료의 종류, 혼합 연료의 혼합비, 산화제, 당량비 등의 연료 특성에 따라 영향을 받게 된다. 이러한 특성치들은 정확히 측정되거나 산출되어야 하며, 특히 화염 스트레치의 경우, 화염 및 유동장 데이터를 이용한 산출이 필요하다.

화염 스트레치 산출을 위한 대표적인 모델식으로, i) Matalon, ii) Chung and Law, iii) Candel and Poinsot에 의해 개발된 3가지 모델 식들이 있다. 본 연구와 함께 제출한 연구, “모델 비교”[15]에서는 이들을 간략한 유도과정과 함께 소개하였다. 모델 식들을 이론적 연구, 수치해석 및 실험 데이터 분석에 적용할 경우 특이점과 장단점들에 관하여 고찰하였다. 특히, 수치해석 및 실험 데이터를 분석하여 화염 스트레치를 산출할 때, 화염 면의 위치/형상과 화염 면 위에서의 특성치들이 주어지는 경우가 많으며, 이러한 상황을 묘사하며, 각 모델 식의 적용에 관하여 고찰하였다. 이러한 화염 스트레치 모델 식들은 서로 다른 형태와 다소 다른 유도과정을 가지고 있어 모델 식들의 적용에 혼동이 발생할 수 있다. 또한, 수치해석 및 실험 데이터를 분석할 경우, 모델 식에 따라 미지수의 발생으로 적용이 명료하지 않거나 복잡한 연산식으로 인해 적용이 용이하지 않을 수 있다.

이러한 혼동을 줄이고 명료한 적용을 위하여, 본 연구에서는 명확화된 산출식을 Table로 제공하여 수치해석 및 실험 데이터의 분석에 사용할 수 있도록 하였다(산출식에 적절한 수치적 차분법을 적용하여 화염 스트레치 및 스트레치 성분들을 산출할 수 있도록 하였다.). 1차원 원형/구형 화염, 정상 상태의 2차원 화염, 비정상 상태의 2차원 화염의 화염 스트레치 산출을 위한 명료한 산술식을 제공하였다. 화염 면 위에서의 좌표로 표현된 산술식들과 기준 좌표계를 사용하는 수치해석이나 실험 영상 데이터에 적용이 편리한 기준 좌표계에서 표현된 산술식들을 Table로 제공하였다.

2차원 정상 상태 화염과 비정상 상태의 화염에 관하여 화염 스트레치를 산출하였으며, 산출과정을 간략하게 묘사하였다. 2차원 정상 상태 화염의 예시로 2차원 층류 블러프 바디 화염의 화염 스트레치를 산출하였다. 반응 진행 변수를 이용하여 화염 면을 정의하고, 화염 면 위의 화염 및 유동 정보를 추출하여 화염 전파 속력을 구한 후 화염 스트레치를 산출하였다. 2차원 비정상 상태 화염의 예시로 조화 진동하는 화염 홀더에 안정화된 층류 V-형상 화염의 화염 스트레치를 산출하였다. 등온선을 이용하여 화염 면을 정의하여 화염 스트레치를 산출하였다. 법선 및 접선 화염 스트레치 성분들과 유동 속도에 의한 스트레치 성분과 화염 전파 속력에 의한 스트레치 성분도 산출하였다.

기 호 설 명

$(x, y, z)$ : 직교 좌표계

$(\vec{i}, \vec{j}, \vec{k})$ : 단위 직교 벡터들

$(ξ_{1}, ξ_{2}, η)$ : 화염 면 직교 좌표계

$(\vec{τ_{1}}, \vec{τ_{2}}, \vec{n})$ : 화염 면 직교 좌표계의 단위 직교 벡터들

$\vec{n}$ : 화염 면 단위 법선 벡터

$\vec{τ_{1}}, \vec{τ_{2}}$ : 화염 면 단위 직교 접선 벡터들

$\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}$ : 델 연산자(직교 좌표계)

$\nabla = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}} + \vec{n} \frac{\partial}{\partial η}$ : 델 연산자(화염 면 직교 좌표계)

$\nabla_{s} = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}}$ : 면-델 연산자

$K_{u}$ : 유동 속도에 의한 화염 스트레치

$Κ_{n, u}$ : 유동 속도에 의한 법선 화염 스트레치

$Κ_{τ, u}$ : 유동 속도에 의한 접선 화염 스트레치

$Κ_{s_{L}}$ : 화염 전파 속력에 의한 화염 스트레치

$Κ_{n, s_{L}}$ : 화염 전파 속력에 의한 법선 화염 스트레치

$F$ : 화염 형상 함수

${\vec{v}}_{f}$ : 화염 이동 속도

${\vec{v}}_{f, n}$ : 화염 면 법선 화염 이동 속도

${\vec{v}}_{f, τ}$ : 화염 면 접선 화염 이동 속도

$\vec{u}$ : 유동 속도

${\vec{u}}_{n}$ : 화염 면 법선 유동 속도

${\vec{u}}_{τ}$ : 화염 면 접선 유동 속도

$s_{L}^{0}$ : 1차원 0-스트레치 평면 화염 층류 화염 속력

$s_{L}$ : 국소 화염 전파 속력

$K$ : 화염 스트레치

$K_{n}$ : 법선 화염 스트레치

$K_{τ}$ : 접선 화염 스트레치

𝜅 : 화염 면 곡률

${()}_{u}$ : 비반응(unburned) 영역의 특성치

${()}_{b}$ : 반응 완료(burned) 영역의 특성치

${()}_{f}$ : 화염 면 특성치

Acknowledgements

이 논문은 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행되었습니다(20206710100060, 분산발전 가스터빈용 수소 전소 저 NOx 연소기 개발, 20214000000310, 탄소중립 고효율 가스터빈 연소기술 에너지 혁신 연구센터).

References

Y. Ju, H. Matsumi, K. Takita, G. Masuya, Combined effects of radiation, flame curvature, and stretch on the extinction and bifurcations of cylindrical CH₄/air premixed flame, Combust. Flame, 116(4) (1999) 580-592. 10.1016/S0010-2180(98)00051-0

A.J. Morales, I.M. Lasky, M.K. Geikie, C.A. Engelmann, K.A. Ahmed, Mechanisms of flame extinction and lean blowout of bluff body stabilized flames, Combust. Flame, 203 (2019) 31-45. 10.1016/j.combustflame.2019.02.002

L.J. Humphrey, V.S. Acharya, D.-H. Shin, T.C. Lieuwen, Modeling the Response of Turbulent Flames to Harmonic Forcing, Combust. Sci. Technol., 189(2) (2017) 187-212. 10.1080/00102202.2016.1202245

G.H. Markstein, Nonsteady Flame Propagation, Pergamon Press, Oxford, (1964). 10.1016/B978-1-4831-9659-6.50005-6

P. Clavin, Dynamic behavior of premixed flame fronts in laminar and turbulent flows, Prog. Energy Combust. Sci., 11(1) (1985) 1-59. 10.1016/0360-1285(85)90012-7

P. Clavin, J.C. Graña-Otero, Curved and stretched flames: The two Markstein numbers, J. Fluid Mech., 686 (2011) 187-217. 10.1017/jfm.2011.318

H.J. Kim, K. Van, D.K. Lee, C.S. Yoo, J. Park, S.H. Chung, Laminar flame speed, Markstein length, and cellular instability for spherically propagating methane/ ethylene-air premixed flames, Combust. Flame, 214 (2020) 464-474. 10.1016/j.combustflame.2020.01.011

B. Karlovitz, D.W. Denniston, D.H. Knapschaefer, F.E. Wells, Studies on Turbulent flames: A. Flame Propagation Across velocity gradients B. turbulence Measurement in flames, Symposium (International) on Combustion, 4(1) (1953) 613-620. 10.1016/S0082-0784(53)80082-2

F.A. Williams, A review of some theoretical considerations of turbulent flame structure, AGARD Conference Proceedings, 164 (1975) 1.

F.A. Williams, Recent Advances in Theoretical Descriptions of Turbulent Diffusion Flames, Turbulent Mixing in Nonreactive and Reactive Flows, (1975) 189-208. 10.1007/978-1-4615-8738-5_5

J. Buckmaster, The Quenching of Two-dimensional Premixed Flames, Acta Astronautica, 6(5-6) (1979) 741-769. 10.1016/0094-5765(79)90031-6

M. Matalon, On Flame Stretch, Combust. Sci. Technol., 31(3-4) (1983) 169-181. 10.1080/00102208308923638

S.H. Chung, C.K. Law, An Invariant Derivation of Flame Stretch, Combust. Flame, 55(1) (1984) 123-125. 10.1016/0010-2180(84)90156-1

S.M. Candel, T.J. Poinsot, Flame Stretch and the Balance Equation for the Flame Area, Combust. Sci. and Tech., 70(1-3) (1990) 1-15. 10.1080/00102209008951608

Y.J. Kim, D.-H. Shin, Comparisons of Flame Stretch Calculation Models and Their Applications, Part I: Model Comparisons, Journal of The Korean Society Combustion, 28(2) (2023) 22-37.

D. Bradley, C.G.W. Sheppart, R. Woolley, D.A. Greenhalgh, R.D. Lockett, The development and structure of flame instabilities and cellularity at low Markstein numbers in explosions, Combust. Flame, 122(1-2) (2000) 195-209. 10.1016/S0010-2180(00)00113-9

J.K. Bechtold, M. Matalon, Hydrodynamic and diffusion effects on the stability of spherically expanding flames, Combust. Flame, 67(1) (1987) 77-90. 10.1016/0010-2180(87)90015-0

P. Cermelli, E. Fried, M.E. Gurtin, Transport relations for surface integrals arising in the formulation of balance laws for evolving fluid interfaces, J. Fluid Mech., 544 (2005) 339-351. 10.1017/S0022112005006695

C. Greenshields, OpenFOAM v9 User Guide, The OpenFOAM Foundation, (2021).

C.K. Wu, C.K. Law, On the determination of laminar flame speeds from stretched flames ,Symposium (International) on Combustion, 20(1) (1985) 1941- 1949. 10.1016/S0082-0784(85)80693-7

G.K. Giannakopoulos, A. Gatzoulis, C.E. Frouzakis, M. Matalon, A.G. Tomboulides, Consistent definitions of "Flame Displacement Speed" and "Markstein Length" for premixed flame propagation, Combust. Flame, 162(4) (2015) 1249-1264. 10.1016/j.combustflame.2014.10.015

M.S. Day, J.B. Bell, Numerical Simulation of Laminar Reacting Flows with Complex Chemistry, Combust. Theory Model., 4(4) (2000) 535-556. 10.1088/1364-7830/4/4/309

A. Nonaka, J.B. Bell, M.S. Day, C. Gilet, A.S. Almgren, M.L. Minion, A Deferred Correction Coupling Strategy for Low Mach Number Flow with Complex Chemistry, Combust. Theory Model., 16(6) (2012) 1053-1088. 10.1080/13647830.2012.701019

M.F.A. Kazakov, Reduced reaction sets based on GRI-Mech1.2: 19-species reaction set, http://www.me.Berkeley.edu/drm/ (1994).

Journal of the Korean Society of CombustionISSN:1226-0959(Print) 2466-2089(Online)한국연소학회

Preview

Comparisons of Flame Stretch Calculation Models and Their Applications Part II: Model Applications

ABSTRACT

MAIN

(1)

Table 1.

Flame stretch model equations

Fig. 1.

A schematic of a flame surface and its curvilinear coordinate system and the reference coordinate system.

Table 2.

Flame stretch expressions in terms of tangential and normal stretches

Table 3.

Flame stretch expressions in terms of flow velocity and flame propagation velocity

Table 4.

Surface unit normal vector definition and corresponding curvature, flame shape scalar function, and flame propagation velocity

Fig. 2.

A schematic of an one dimensional outwardly propagating circular flame.

(2)

(3)

(4)

(5)

(6)

Table 5.

Flame stretch analyses on one dimensional outwardly propagating flame

Fig. 3.

A schematic of an one dimensional outwardly propagating spherical flame.

(7)

(8)

Fig. 4.

A schematic of a 2 dimensional flame.

(9)

(10)

(11)

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

Table 6.

Flame stretch analyses on two dimensional steady flame

(21)

Table 7.

Flame stretch analyses on two dimensional unsteady flame

(22)

Fig. 5.

(a) A schematic of a 2 dimensional laminar bluff body flame and (b) temperature and flow direction of numerical simulation result.

Fig. 6.

(a) Flame surface location, (b) flame propagation speed, (c) flame stretch, normal stretch and tangential stretch, and (d) flame stretch, stretch by flow velocity, and stretch by flame propagation speed, of the 2 dimensional laminar bluff body flame.

Fig. 7.

(a) An experimental example [3], (b) a schematic of a 2 dimensional laminar fluctuating V-shape flame induced by an oscillating flame holder, and (c) temperature and flow direction of numerical simulation result.

Fig. 8.

Acknowledgements

References