1. 서 론
2. 수치해석 방법
2.1 수치해석 모델
2.2 작동유체 및 해석조건
2.3 화학반응 메커니즘
3. 결과 및 토의
3.1 Primary cracking 조건 해석 결과
3.2 Secondary cracking 조건 해석 결과
4. 결 론
1. 서 론
스크램제트 엔진은 지구 대기권 내에서 마하 5 이상으로 비행 가능한 극초음속 순항비행체용 공기흡입 추진기관으로서 로켓 추진기관 대비 높은 비추력 특성과 광범위한 속도 영역에서의 운용 유연성을 가진다[1,2]. 그러나 스크램제트 엔진을 이용한 극초음속 순항 비행이 가능하기 위해서는 고속비행으로 인한 동체의 공력가열과 엔진 연소실의 고온가열 문제를 해결해야 할 뿐만 아니라[3], 스크램제트의 초음속 연소실 내에서의 복잡하고 매우 빠른 공기 유동에서도 연료를 효과적으로 혼합하고 연소시킬 수 있어야 한다[1]. 이를 위하여 전세계적으로 탄화수소 항공유를 이용한 능동재생냉각시스템이 연구되고 있는데[1], 비행체에 탑재된 액체 연료를 냉각이 필요한 곳에 냉매로서 순환시키는 능동재생냉각시스템을 적용하면 극초음속 비행에 따른 동체와 엔진의 극심한 가열문제를 효과적으로 해결할 수 있다. 뿐만 아니라 냉매로 순환하면서 고온으로 가열되거나 다양한 저분자량 탄화수소 성분들로 분해된 연료가 스크램제트 엔진의 초음속 연소실에 공급될 경우 연료가 액체 상태일 때보다 훨씬 빨리 공기와 혼합 및 연소되므로, 초음속 연소 효율이 크게 높아짐과 동시에 추진기관 시스템의 전체적인 싸이클 성능도 향상된다[1,4]. 그런데, 일반적으로 탄화수소 항공유를 이용한 재생냉각은 채널 내부에서의 상변화를 방지하고 열전달 특성을 증대시키기 위하여 임계 압력 이상에서 이루어지도록 설계하므로, 연료가 냉각채널 내에서 냉매로 순환하면서 임계 온도 이상으로 가열되면 결국 초임계(supercritical) 상태까지 도달하게 된다[5].
따라서, 실제로 운용 가능한 극초음속 비행체용 재생냉각시스템과 이와 연동된 스크램제트 엔진을 개발하기 위해서는 재생냉각시스템용 미세채널 내에서의 초임계 탄화수소 연료의 유동/열전달/흡열분해 특성을 파악하며, 재생냉각시스템을 통과하여 스크램제트 엔진의 연소실로 공급된 초임계 상태 또는 흡열 분해된 연료의 초음속 공기 유동으로의 분사/분무/혼합/연소 특성을 규명하기 위한 일련의 체계적이고 심층적인 연구가 수행되어야만 한다[6]. 이를 위하여 지난 몇 년간 본 연구그룹에서는 초임계 탄화수소 항공유의 열물리적 물성치 획득 기법을 개발하고 다양한 탄화수소 순수물질 및 혼합물에 대한 밀도, 정압비열, 점도, 열전도도 예측 성능을 광범위한 온도 및 압력 범위에서 정량적으로 확인하였다[7,8].
극초음속 비행체용 능동재생냉각시스템의 설계를 위한 다음 단계는 초임계 탄화수소 항공유의 흡열 및 냉각 특성을 결정하는 재생냉각 채널 내부에서의 일련의 복잡한 물성치/유동/열전달/흡열분해 사이의 열유체역학적/화학적 상호작용의 메커니즘을 규명하고 그 특성을 정확하게 예측/분석하는 기술을 개발하는 것이다. 그 중에서도 탄화수소 항공유의 흡열분해 화학반응을 효과적으로 시뮬레이션하는 기법은 능동재생냉각시스템 설계에 필수적인 기술로서 현재 전세계적으로 많은 연구가 진행되고 있다. 특히, Ward 등은 미세채널 내에서 n-decane(C10H22)과 n-dodecane(C12H26)에 대한 흡열분해 실험을 수행하고, 채널 내부의 온도/압력/유량에 따른 열분해 생성물 분석 결과로부터 연료의 분해율(또는 전환율)이 20% 이하일 때에는 기체 및 액체 생성물들의 구성 성분과 비율이 거의 변화하지 않음을 관찰하고 이를 토대로 global one-step 흡열분해 화학반응 모델인 PPD(Proportional Product Distribution) 모델을 제안하였다[9,10].
그 후 여러 연구 그룹에서 PPD 모델을 개선하고 발전시키려는 노력을 지속적으로 투입하였는데, 특히 Zhang 등은 n-dodecane을 이용한 미세채널 흡열분해 실험을 수행하고 기체/액체 생성물을 분석한 결과 n-dodecane의 전환율에 따라 흡열분해 특성이 크게 primary, secondary, severe cracking의 세 가지 영역으로 구분됨을 확인하였다[11]. 특히, primary cracking은 전환율 13% 이하, secondary cracking은 13∼71% 사이, severe cracking은 71% 이상의 전환율에서 발생함을 확인하고, primary cracking 영역에서는 Ward 등이 제안한 PPD 모델이 유효하지만, secondary cracking 영역에서는 alkane과 alkene이 추가 분해되어 MAH와 cyclo-alkenes 등이 생성되는 사실로부터 C8H18로 대표되는 alkane과 C8H16으로 대표되는 alkene의 추가 분해 과정을 고려하는 secondary cracking 반응 모델을 새롭게 제안하였다. 한편, Jiang 등은 이러한 PPD 모델의 정확도를 더욱 높이기 위하여 n-decane을 이용한 미세채널 흡열분해 실험을 수행하고 그에 대한 생성물 분석 결과로부터 one-step global reaction model의 stoichiometric coefficients를 고정된 상수가 아닌 전환율과 반응 압력에 따라 변화하는 함수로 표현하는 DGR (Differential Global Reaction) 모델을 제안하였다[12].
이러한 흡열분해 화학반응 시뮬레이션 연구 결과로부터 국내에서는 Lee 등[13]이 n-dodecane을 연료로 사용하여 Zhang 등[11]이 제안한 primary cracking PPD 모델을 적용하여 초임계 압력 조건에서 전환율 13%의 가열 조건에 대한 수치해석을 수행하였다. 그 결과 내경 2 mm의 원통형 미세채널 내부에서 일정한 열유속 조건에 대하여 n-dodecane의 유량 변화에 따른 가열 및 흡열분해 특성을 파악하였고, 그 결과 열분해 반응을 고려하는 경우 연료의 흡열 특성으로 인해 미세채널 출구에서의 연료 온도가 더 낮아질 뿐만 아니라 연료 전환율에 따른 분해 생성물의 질량 분율도 Zhang 등의 연구에서 제시한 실험 결과와 매우 정확하게 일치함을 확인하였다.
따라서 본 연구에서는 극초음속 비행체용 재생냉각 미세채널 내부에서 탄화수소 항공유의 흡열분해 화학반응을 보다 정확하게 시뮬레이션하는 기법을 개발하기 위하여 초임계 압력 조건에서 미세채널 내부를 유동하면서 가열되어 초임계 온도 조건에서 흡열분해되는 n-dodecane에 대한 전산유체해석을 수행하였다. 특히 Lee 등[13]의 연구 결과를 확장하기 위하여, Zhang 등[11]이 개발한 secondary cracking 모델을 추가하여 전환율 13% 이상으로 분해되는 높은 가열 열유속 조건에 대한 해석을 수행하고 secondary cracking 유무에 따른 흡열분해 특성을 파악함과 동시에, 본 연구의 해석 결과와 이전 연구의 실험 결과와의 비교를 통하여 multi-step PPD 모델과 본 연구에서 적용한 수치해석 기법의 정확성을 검증하고자 한다.
2. 수치해석 방법
2.1 수치해석 모델
극초음속 비행체용 재생냉각시스템 내부에 적용되는 미세채널을 모사하기 위하여 원통관을 2차원 축대칭 형상으로 모델링하여 수치해석을 수행하였다. 채널의 내경은 2 mm이며, 총 길이는 1,100 mm로서, 그중 입구로부터 950 mm는 일정한 열유속을 가하는 가열부, 나머지 150 mm는 단열부로 설정하였는데, 이는 선행 연구들에서와 동일한 형상이다[11,13]. 본 연구에서 사용한 원통관의 전체 형상 및 생성된 격자의 일부분을 Fig. 1에 나타내었는데, 격자는 정렬격자계로 생성하였고, 벽면과 유체 사이의 열전달을 보다 정확하게 모사하기 위하여 벽근처의 격자를 조밀하게 생성하였다. 특히, 본 연구에서는 Lee 등[13]의 연구에서 사용한 66,000개와 Zhang 등[11]의 연구에서 사용한 369,400개를 절충하여, k-ω SST 난류 모델 적용시 벽면에서의 y+ 값이 모든 계산 조건에서 5 이하로 유지됨과 동시에 적정한 계산 시간 동안에 흡열 분해반응 해석이 진행되도록 총 격자수를 220,000(8800×25)개로 설정하였다.
해석 Solver는 ANSYS CFD 2022R2 Fluent의 pressure- based, steady RANS를 사용하였고, 난류 및 화학반응 모델과 각종 수치해석 기법들은 모두 Lee 등[13]의 선행연구와 동일하게 설정하였다. 본 해석에 사용된 모델 및 수치해석 기법들은 Table 1에 정리하였다.
Table 1.
Simulation methods
2.2 작동유체 및 해석조건
작동유체(working fluid)로는 서론과 2.3절에서 언급한 바와 같이 흡열분해 화학반응용 PPD 모델이 제안되어 있는 n-dodecane(C12H26)을 사용하였으며, n-dodecane의 밀도, 정압비열, 점도, 열전도도 등의 열물리적 물성치는 일정 압력 조건에서 NIST SUPERTRAPP[14]을 이용하여 획득한 후 다항식으로 각각 피팅하여 계산에 적용하였다.
한편, 계산에 사용한 조건들은 Table 2에 나타내었는데, 특히 채널 내부의 압력과 입구 연료 온도는 n-dodecane의 임계 압력(1.806 MPa)과 임계 온도(658.1 K)보다 높게 설정하였으며, 이는 Zhang 등[11]과 Lee 등[13]의 선행 연구들과 동일한 조건이다. 특히, Zhang 등[11]의 선행 연구에서는 연료를 Preheater를 통해 400°C 가까이 가열 후 Reactor로 공급하여 열분해가 되도록 실험을 진행하고 그와 동일한 Reactor 입구 조건으로 해석을 수행하였기 때문에 본 연구에서도 그와 동일한 조건으로 해석을 수행하였다. 그러나, 입구 온도를 연료의 임계점 이하로 설정하여도 흡열분해 전산해석을 수행하는데 특별히 제한되는 사항은 없으며, 다만 상온 상태에서 연료가 가열되기 시작한다면 흡열분해되기 위해 필요한 가열량이 더 크거나 체류시간이 더 길어져야 하는 점을 고려할 필요가 있다. 그리고, 본 연구에서는 입구 질량유량을 3 kg/h로 고정하였고, 연료 전환율 13%∼82%까지의 결과를 획득하기 위하여 벽면 열유속을 65 kW/m2부터 160 kW/m2까지 광범위하게 변화시키면서 계산하였다.
Table 2.
Simulation conditions
| Parameter | Value |
| Pressure | 3 MPa |
| Inlet temperature | 665 K |
| Mass flow rate | 3 kg/h |
| Heat flux | 65 ~ 160 kW/m2 |
2.3 화학반응 메커니즘
흡열분해 화학반응 해석에는 Zhang 등[11]이 수립한 n-dodecane의 PPD 모델을 적용하였다. 이 모델은 n-dodecane의 분해율을 기준으로 초기 분해율 약 13%까지 적용할 수 있는 primary cracking PPD 모델과 이후 13%에서 약 80%까지의 분해율에 대해 추가로 적용이 필요한 secondary cracking PPD 모델로 구성되는데, 우선 primary cracking PPD 모델 반응식은 다음과 같다[11,13].
n-dodecane은 식 (1)과 같이 11개의 화학종으로 분해되며, 반응 속도 상수는 아레니우스 식(Arrhenius form)으로 표현하였고, 아래 식 (2)와 같다.
여기에서 와 는 각각 pre-exponential factor와 활성화 에너지(activation energy)를 나타내며, primary cracking의 경우 는 2.466×1014 s-1이며, 는 225.8 kJ/mol이다 [11,13].
다음으로 secondary cracking의 경우에는 두가지의 반응식이 추가되는데, 이는 분해율이 13% 이상이 되면 C8H18으로 대표되는 alkane 그룹과 C8H16으로 대표되는 alkene 그룹이 추가 분해되기 때문이다. 이들의 반응식은 아래 식 (3), (4)와 같다[11].
식 (3)에서 는 7.385×1014 s-1,는 209.6 kJ/mol이며, 식 (4)의 는 2.631×1014 s-1,는 217.8 kJ/mol이다[11].
3. 결과 및 토의
3.1 Primary cracking 조건 해석 결과
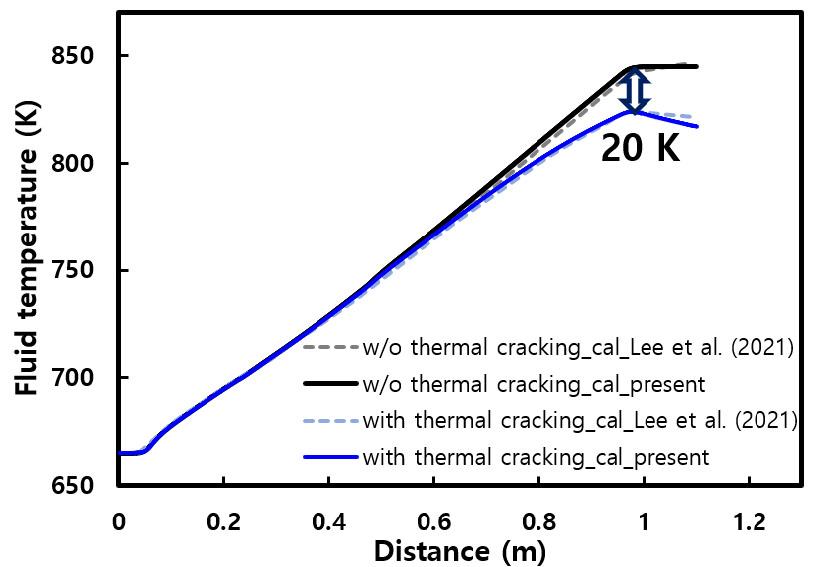
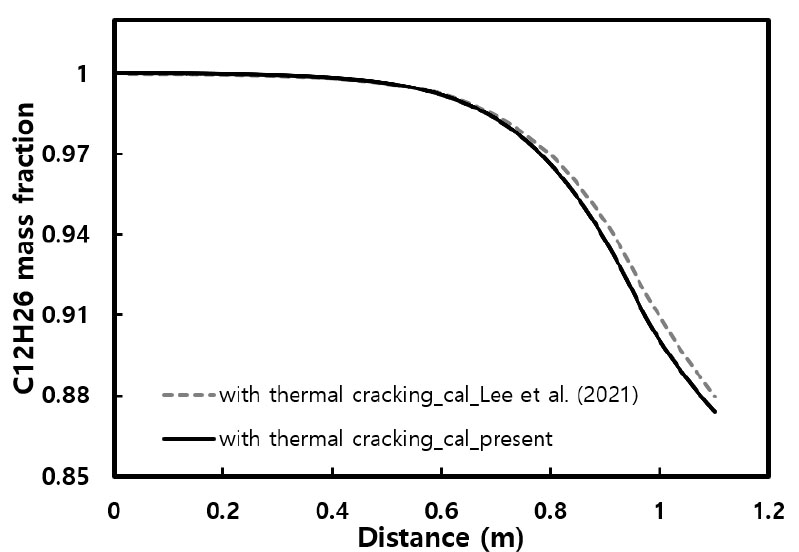
본 절에서는 우선 primary cracking이 지배적인 조건을 고려하기 위하여 벽면 열유속을 65 kW/m2로 설정하여 해석한 결과를 제시하였다. Fig. 2에는 미세채널 위치에 따른 n-dodecane의 중심축 온도 분포를 도시하였는데, 채널 입구에서 665 K으로 공급된 연료는 벽면으로부터의 열전달에 의해 가열되어 온도가 지속적으로 상승하게 된다. 그런데 입구로부터의 거리가 약 0.6 m 인 지점부터는 열분해 반응을 고려한 경우와 그렇지 않은 경우의 온도 분포가 서로 차이를 나타내기 시작하여, 채널 출구 부분에서는 열분해 반응을 고려한 경우가 약 20 K 정도 낮게 나타나는 것을 알 수 있다. 이러한 경향은 Lee 등[13]의 선행 연구에서도 동일하게 나타나는 현상인데, 이는 n-dodecane이 흡열 분해되면서 벽면으로부터 공급되는 에너지의 일부를 흡수하기 때문이며, 이러한 사실은 Fig. 3에 보이는 바와 같이 입구로부터의 거리가 약 0.6 m인 지점부터 n-dodecane의 질량 분율이 낮아지는 사실로부터 확인할 수 있다.
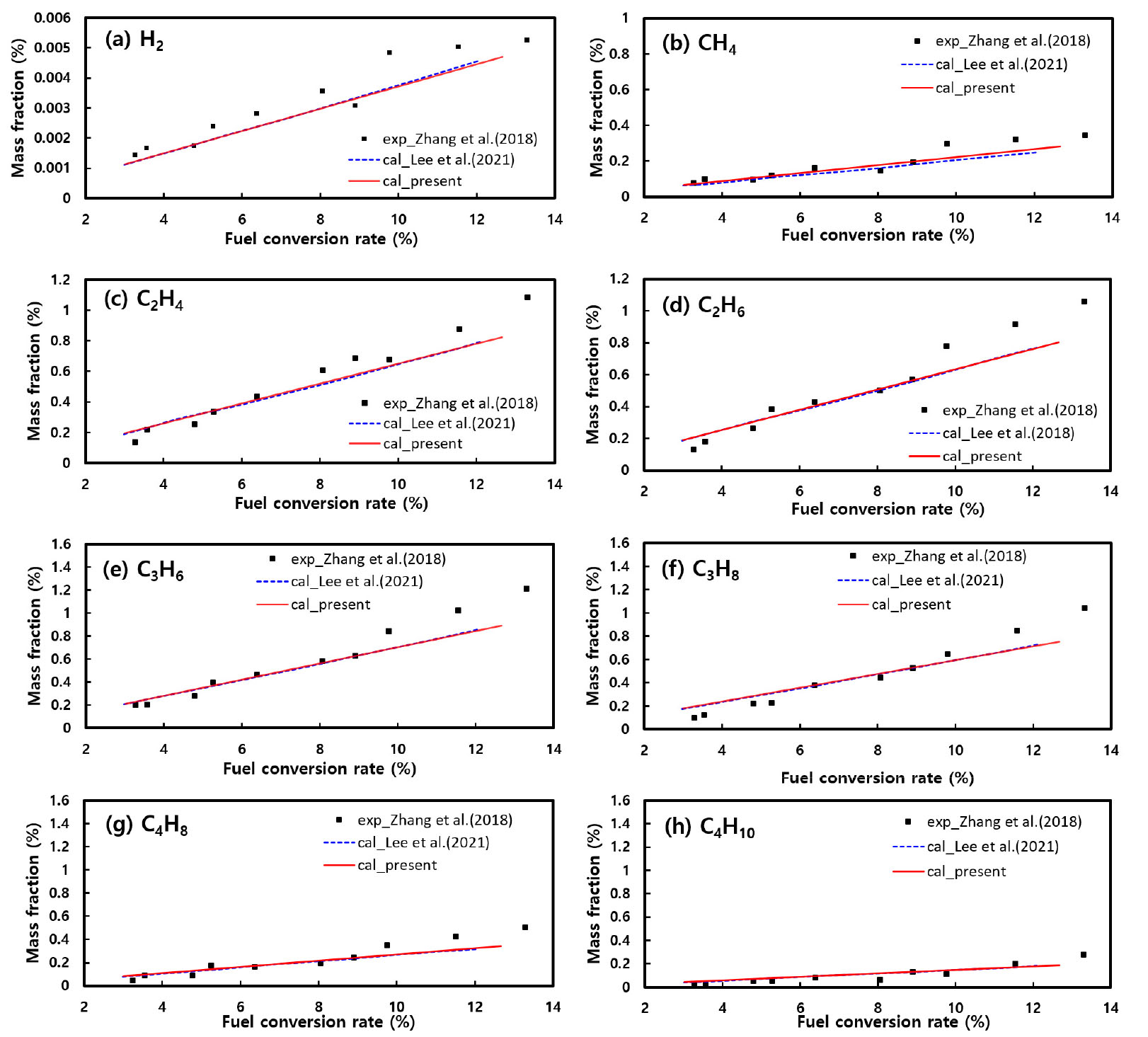
Fig. 4에는 n-dodecane의 흡열분해 반응으로부터 생성된 화학종들의 질량 분율 해석 결과를 동일한 조건에서 수행한 이전의 실험[11] 및 해석[13] 결과와 비교하였다. 결과를 살펴보면 본 연구의 결과가 이전의 해석 결과와 거의 일치할 뿐만 아니라 실험으로부터 획득된 각 화학종들의 질량 분율도 비교적 정확하게 예측하고 있음을 확인할 수 있다. 다만 전체적으로 전환율이 10% 이상이 되면 각 화학종들의 질량 분율 해석 결과가 실험 결과와 상이한 경향이 관찰되는데, 이는 전환율이 증가할수록 분해 생성물들의 질량 분율은 비선형적으로 증가하지만 primary cracking 만을 고려하는 PPD 모델은 기본적으로 전환율에 따른 분해 생성물들의 질량 분율을 단지 선형적으로만 계산하기 때문이다. 따라서 이러한 문제를 해결하기 위해서는 전환율이 10% 이상으로 증가하는 경우 다음 절에서 언급하는 바와 같이 secondary cracking을 추가적으로 고려해야만 한다.
한편, 채널 위치에 따른 연료의 온도 및 질량 분율 분포는 Figs. 2와 3에서 Lee 등[13]의 선행 연구 결과와 본 연구의 해석 결과를 비교하였는데, Fig. 4에서와 마찬가지로 두 연구 결과가 거의 유사하므로, 따라서 본 연구의 해석기법이 미세채널 내부에서 n-dodecane의 흡열분해 반응을 정상적으로 시뮬레이션함을 확인할 수 있다. 그러나, Figs. 2와 3에서는 본 해석 결과와 선행 연구 결과가 완벽히 일치하지는 않고 있는데, 이에 대한 원인으로는 2.1절에서 언급한 바와 같이 본 연구의 총 격자 수가 3배 이상 많기 때문인 것으로 판단되며, 따라서 본 연구의 결과가 약간 더 정확할 것으로 추론된다.
3.2 Secondary cracking 조건 해석 결과
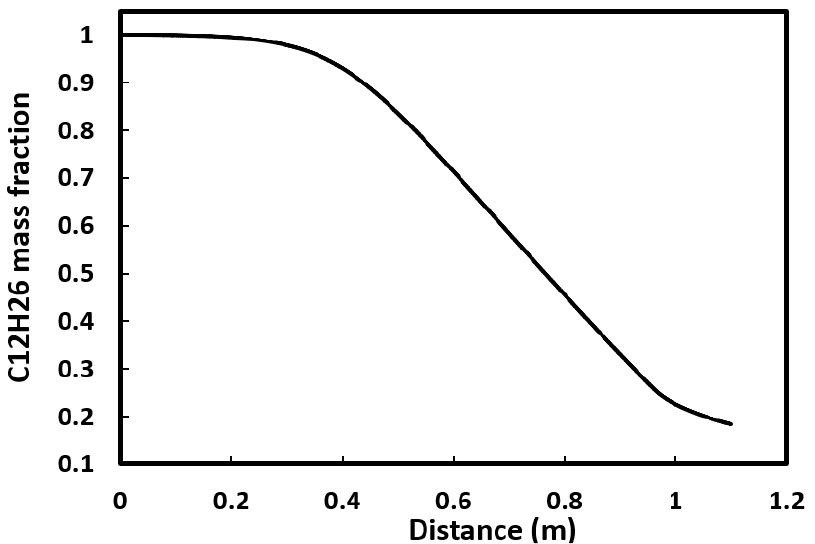
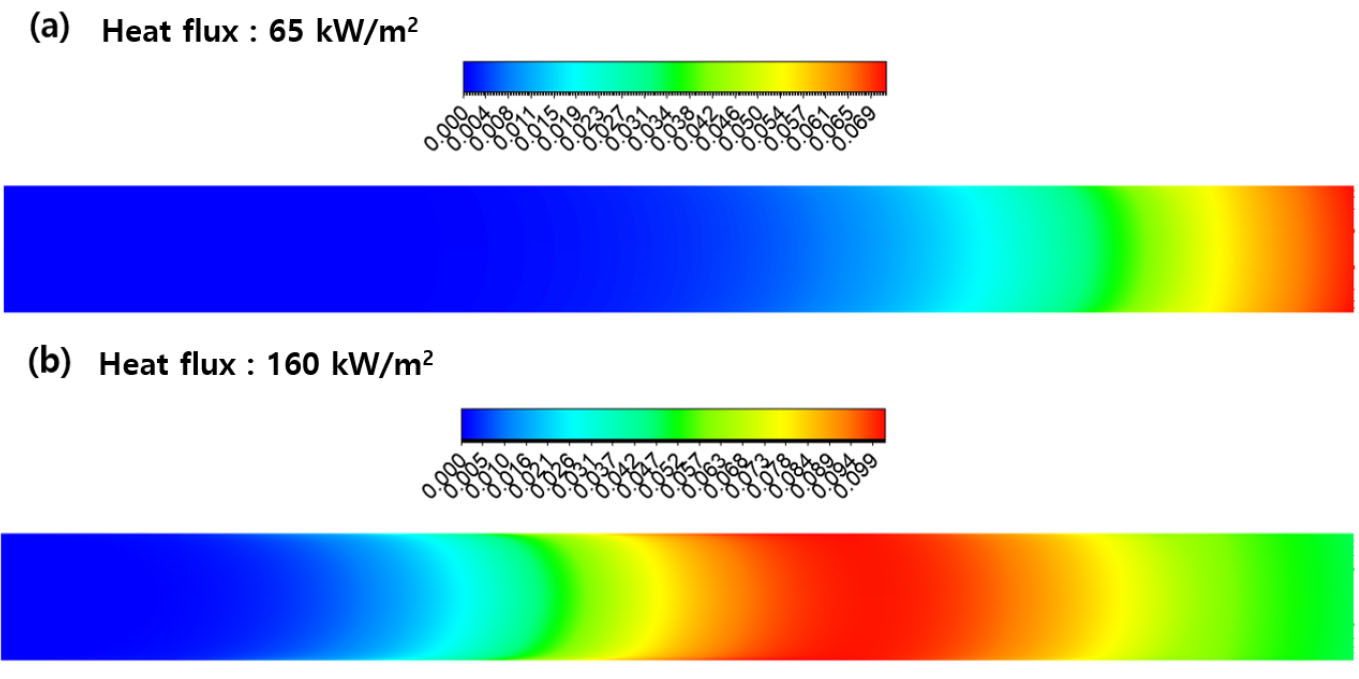
다음으로는 secondary cracking이 활발하게 발생하는 조건에 대한 해석을 수행하였는데, 특히 연료의 전환율을 높이기 위하여 벽면 열유속을 65 kW/m2부터 160 kW/m2까지 다양하게 증가시키면서 해석하였다. 그 결과 Fig. 5에 보이는 바와 같이 160 kW/m2 조건에서 미세채널 출구에서의 n-dodecane 질량 분율이 0.2 이하로 감소하였으며 그에 따른 연료 전환율은 81.6%인 것으로 확인되었다.
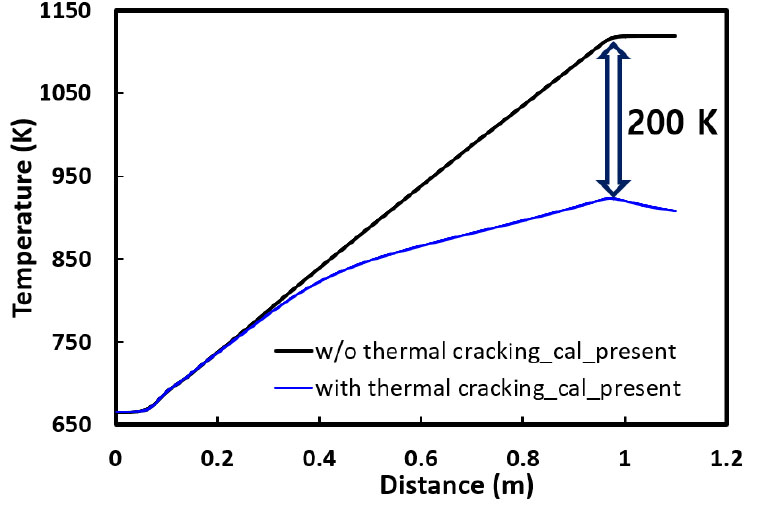
Fig. 6에는 벽면 열유속 160 kW/m2 조건에서 의 미세채널 위치에 따른 n-dodecane의 중심축 온도 분포를 도시하였는데, 열분해를 고려하는 경우와 그렇지 않은 경우의 온도를 비교해 보면 입구로부터의 거리가 약 0.3 m인 지점부터 두 경우에 차이가 발생하기 시작하며 그 차이는 점점 크게 벌어져 채널 출구에서는 200 K까지 그 차이가 증가함을 알 수 있다. 이는 Fig. 5에 보이는 바와 같이 n-dodecane이 약 0.3 m인 지점부터 분해되기 시작하여 채널 출구에서는 약 82%까지 분해되면서 벽면으로 유입되는 열을 상당 부분 흡수하였기 때문이다. 이러한 사실로부터 재생냉각 채널 내부에서 탄화수소 연료의 흡열 분해반응을 이용하면 서론에서 언급한 바와 같이 극초음속 비행에 따른 동체와 엔진의 극심한 가열문제를 효과적으로 해결 가능함을 명확하게 확인할 수 있다.
Fig. 7에는 3.1절의 primary cracking 조건과 본 절의 secondary cracking 조건에서 C8H16으로 대표되는 alkene의 미세채널 중앙 단면에서의 질량 분율 분포를 비교하였다. 그림에서 확인할 수 있는 바와 같이 primary cracking 조건에서는 C8H16이 채널 내부에서 꾸준히 증가하는 경향을 보이는 반면에 secondary cracking 조건에서는 primary cracking에 의해 생성된 C8H16이 secondary cracking에 의하여 추가 분해되므로 채널 중간 부분에서 최대의 질량 분율을 나타내지만 채널 출구에 가까워질수록 질량 분율이 감소하는 경향을 보이고 있음을 확인할 수 있다.
Fig. 8에는 벽면 열유속 160 kW/m2 조건에서 n-dodecane의 전환율에 따른 각종 기체 생성물들의 질량 분율 해석 결과를 Zhang 등[11]의 실험 및 계산 결과와 비교하였다. 그림에서 확인할 수 있는 바와 같이 본 연구의 결과가 secondary cracking 조건에서도 다양한 기체 생성물들의 질량 분율 분포를 이전의 실험 및 해석 결과와 매우 유사하게 예측하고 있다.
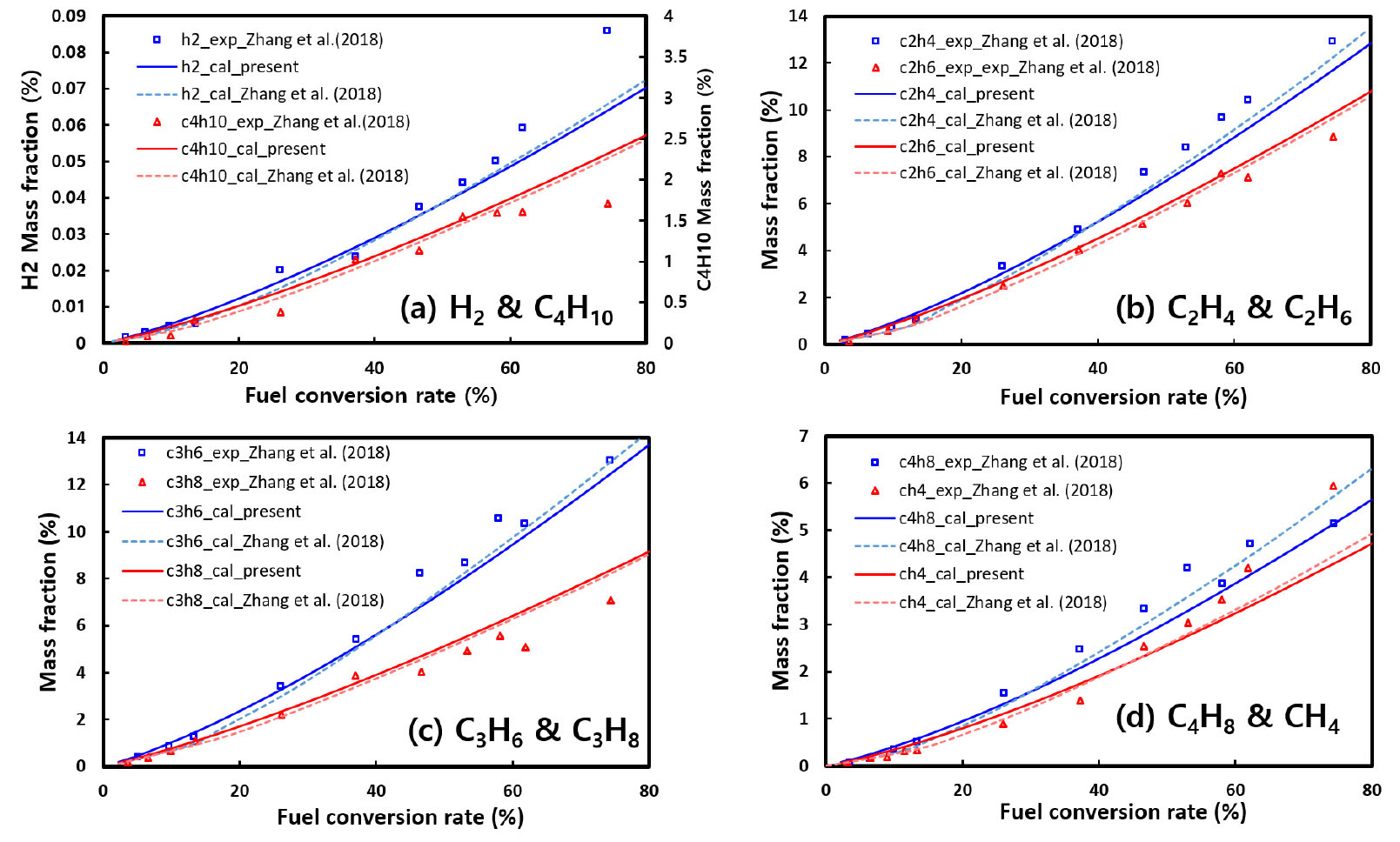
Fig. 8.
Comparison of mass fraction of gaseous products with respect to the fuel conversion rate with the experimental and numerical results by Zhang et al. [11].
한편 Fig. 9에는 액체 생성물 중 C7H8로 대표되는 Monocyclic Aromatic Hydrocarbons(MAH)와 C7H12로 대표되는 Cyclo-alkenes의 질량 분율 해석 결과를 이전 연구결과와 비교하였으며, Fig. 8에서와 마찬가지로 주요 액체 생성물들의 분포를 이전의 실험 및 해석 결과와 매우 유사하게 예측하고 있음을 확인할 수 있다.
그러나, 전환율이 60% 이상이 되면 해석에 의한 예측 결과와 실험 결과의 오차가 커지는 경향이 관찰되며, 특히 Fig. 8(a)의 H2 질량 분율과 Fig. 8(d)의 CH4 질량 분율, 그리고 Fig. 9의 경우에 오차가 큰 것을 확인할 수 있다. 이러한 결과의 원인으로는 서론에서 언급한 바와 같이 secondary cracking 영역은 일반적으로 전환율 기준으로 13~71%이며 그 이상으로 연료가 분해되면 severe cracking이 발생하는 것으로 알려져 있으므로, Figs. 8, 9의 결과로부터 전환율이 매우 높은 영역에서 오차가 커지는 경향은 해석에서 고려하지 않은 severe cracking이 실험에서는 실제로 발생하였기 때문인 것으로 추론된다. 그러나, 이러한 severe cracking은 아직까지 정확한 해석 모델이 제시되어 있지 않아 본 연구에서는 고려하지 않았으며, 따라서 70% 이상의 높은 전환율에서도 보다 정확하게 해석을 수행하기 위해서는 향후 severe cracking 모델에 대한 추가 연구가 필요할 것으로 판단된다.
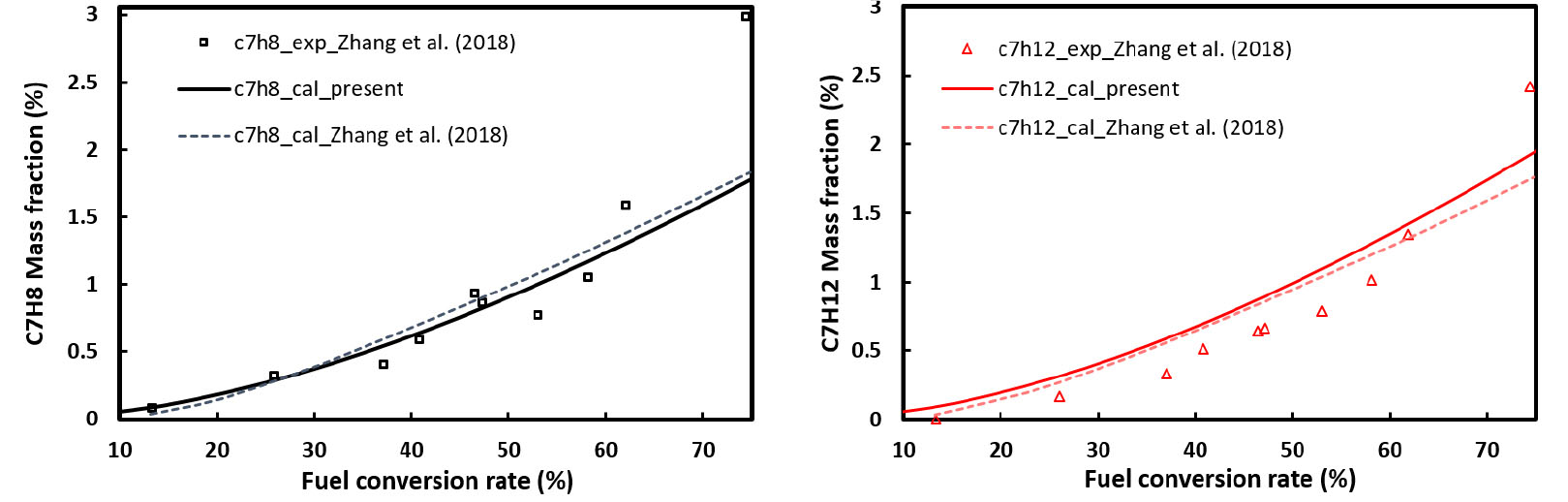
Fig. 9.
Comparison of mass fraction of liquid products with respect to the fuel conversion rate with the experimental and numerical results by Zhang et al. [11].
4. 결 론
본 연구에서는 극초음속 비행체용 재생냉각 미세채널 내부에서 탄화수소 항공유의 흡열분해 화학반응을 보다 정확하게 시뮬레이션하는 기법을 개발하기 위하여, 초임계 압력 조건에서 미세채널 내부를 유동하면서 가열되어 초임계 온도 조건에서 흡열분해되는 n-dodecane에 대한 전산유체해석을 수행하였다. 특히 secondary cracking을 포함하는 multi-step PPD 흡열분해 반응모델을 적용하여 전환율 13% 이상으로 분해되는 높은 가열 열유속 조건에 대한 해석을 수행하고 secondary cracking 유무에 따른 흡열분해 특성을 파악함과 동시에, 본 연구의 해석 결과와 이전 연구의 실험 결과와의 비교를 통하여 PPD 모델을 적용한 수치해석 기법의 정확성을 검증하였다.
우선, 벽면 열유속 65 kW/m2인 primary cracking 영역에서는 최대 분해율이 13%로서 흡열 분해반응 유무에 따른 온도차가 20 K으로 확인되었다. 또한, 생성된 8가지 화학종의 질량분율을 실험 결과와 비교한 결과, 전환율이 증가함에 따라 질량분율이 선형적으로 증가하였다. 한편, 벽면 열유속 160 kW/m2일 때에는 최대 분해율이 81.6%로서 primary cracking과 secondary cracking을 모두 포함하는 PPD 모델을 적용하여 해석을 수행하였으며, 이때 흡열분해반응 유무에 따른 온도차는 200 K으로 매우 크게 나타났다. 특히 secondary cracking 영역에서는 primary cracking에서 생성된 alkane 그룹(C8H18)과 alkene 그룹(C8H16)의 화학종이 재분해되며, 그에 따라 C7H8로 대표되는 Monocyclic Aromatic Hydrocarbons(MAH)와 C7H12로 대표되는 Cyclo-alkenes이 추가로 생성되는 것을 확인하였고, 주요 기체 및 액체 생성물들의 전환율에 따른 질량분율 분포가 이전 연구의 해석 및 실험 결과와 잘 일치함을 확인하였다.
그러나 PPD 모델은 기본적으로 흡열분해 화학반응으로부터 생성된 화학종들이 선형적인 분포를 가지는 것으로 가정한 모델이기 때문에 실제로 존재하는 흡열분해 생성물들의 전환율에 따른 비선형성을 구현하지는 못하는 한계가 존재하며, 이러한 사실은 primary 및 secondary cracking 영역의 계산 결과에서 전환율이 커질수록 오차가 커지는 사실로부터 확인할 수 있었다. 이러한 한계를 극복하기 위해서는 서론에서 언급한 바와 같이 DGR 모델과 같은 보다 정교한 모델을 적용하여 분해 생성물들의 생성 비율을 전환율을 포함한 다양한 파라미터들의 함수로 표현할 수 있어야 한다.
결론적으로, 본 연구에서 사용된 secondary cracking을 포함하는 multi-step PPD 모델과 이를 적용한 초임계 조건에서의 흡열분해 화학반응 해석 기법은 탄화수소 항공유의 재생냉각 미세채널 내부 유동/열전달/흡열분해 특성을 예측하기 위한 공학적인 해석 기법으로 적용이 가능하며, 이를 좀 더 정교하게 수정 및 발전시킴으로써 향후 극초음속 비행체용 재생냉각시스템의 설계 및 해석에 유용하게 활용할 수 있을 것으로 기대된다.