1. 서 론
2. 실험장치 및 방법
2.1 V-shape 버너
2.2 프랙탈 형상의 난류생성판
2.3 열선유속계
2.4 실험조건 및 버너의 난류 정보
3. 결과 및 고찰
3.1 중심축에 따른 난류특성
3.2 (r, z) 평면 유동장 특성
4. 결 론
1. 서 론
난류연소는 발전용 가스터빈 및 왕복동 내연기관, 보일러와 같은 연소시스템에서 흔히 나타나며 낮은 오염물질배출과 높은 에너지 밀도를 구현하기 위하여 대부분 희박 예혼합연소방식을 적용하고 있다[1]. 이와 연관되어 난류-화염간의 상호작용 및 난류 예혼합연소의 전반적인 현상을 이해하기 위하여 다양한 난류화염 구조에서 연구하고 있다(예를 들어 분젠형 화염(Bunsen flame), V형 화염(V-shape flame), 대향류 화염(counter flow flame) 및 스월러 화염(swirl flame), 구형 챔버 화염(spherical flame) [2-6]. 이러한 난류 예혼합연소특성을 평가하기 위한 기초연구 목적으로 난류유동장을 생성하거나, 저선회 연소기(low swirl combustor)의 중앙 난류 생성기(turbulent generator)로 타공판 또는 매쉬(mesh)를 난류생성판으로 사용한다[7], [8], [9], [10], [11]. 하지만 이러한 방법은 난류생성판 주변에 높은 난류강도를 생성할 수 있지만 후류지점으로 갈수록 난류강도가 급격히 낮아져서 실제로 화염이 존재하는 구간에는 다소 낮은 난류강도에 노출된다. 이러한 단점을 극복하는 한 가지 방법으로 Hurst와 Vassilicos는 프랙탈(Fractal, 이하, 프랙탈) 형상의 격자를 난류생성판으로 사용하였다[12], [13]. Hurst와 Vassilicos가 제안한 프랙탈 형상의 격자는 총 세 가지로 크로스(cross, 이하, 크로스), 스퀘어(square, 이하, 스퀘어), I 타입이며, 이러한 프랙탈 격자는 프랙탈의 여러 형상변수들이 정해지면 수학적으로 다양한 길이스케일(length scale)을 가지는 일정한 패턴의 구조가 완성된다. 이처럼 다양한 길이스케일로 인하여 난류강도는 최대값에 도달할 때까지 각각의 난류생성지점에서 난류화가 진행되어 중첩되는 “난류 발달영역”과 최대 난류강도 지점 이후 난류강도가 줄어드는 “난류 붕괴영역”이 존재한다(이에 대한 자세한 내용은 2.4절에서 설명된다). 이러한 난류강도 영역의 구분은 프랙탈 격자가 일반타공판 및 매쉬 타입에 비해 뚜렷하며, 프랙탈 형상이 좀 더 넓은 난류강도 발달영역으로 인하여 최대난류강도의 위치는 좀 더 후류지점에서 나타나게 된다. 이로 인해 화염은 비교적 높은 난류강도에 노출되게 되어 난류연소속도를 증가 시킬 수 있게 된다. 이렇듯 화염에 직접적으로 영향을 주는 난류유동의 특성을 파악하는 것은 난류화염의 전반적인 특성을 이해하는데 있어 매우 중요하다.
프랙탈 형상을 적용한 난류생성판의 비반응장 유동 특성은 몇몇 연구자들에 의해 보고되었다. 대표적인 연구로 Sponfeldner는 화염 안정화 장치(flame stabilizer)가 없는 사각 V_shape 버너에서 스퀘어타입 프랙탈 격자를 적용한 난류생성판의 난류유동 특성을 일반 격자(매쉬)와 비교하였다[13]. 여기서 사용한 스퀘어 격자는 막힘률(), 두께 축소율(), 형상 반복 횟수()가 변경됨에 따라 총 4가지를 사용하였다(이에 대한 용어 설명은 2.2절에서 설명된다.). 우선 중심축을 따라 비반응장의 난류강도 값을 통해 적절한 형상매개변수를 사용하면 최대 난류강도의 크기는 일반매쉬와 유사하면서 좀 더 후류지점에서 생성 될 수 있음을 보였으며, 2D 등방성(isotropy) 및 균질성 조사를 통하여 형상 반복횟수 과 mesh size의 감소는 등방성(isotropy, )의 값과 비균질성(inhomogeneity)이 증가할 수 있음을 보여주었다. 하지만 다른 막힘률을 가지는 일반매쉬( = 60%)와 스퀘어타입( = 35, 37%)의 비교로 인해 스퀘어 프랙탈의 난류화 증대 효과가 뚜렷하게 나타나지 않았고, 총 4가지의 스퀘어 프랙탈 난류생성판을 사용하였기 때문에 프랙탈 형상매개변수에 따른 경향은 확인할 수 없었다.
또 다른 연구로 Verbeek은 Vassilicos 연구팀에서 제안된 프랙탈 형상 중 크로스와 스퀘어타입을 선정하였으며 형상매개변수에 따른 난류 V-shape 화염특성을 확인하기 전에 비반응장 난류유동을 우선적으로 조사하였다[14]. 프랙탈 난류생성판은 = 25, 35, 45%, = 0.29, 0.4, 0.7, 1.0, = 3인 형상매개변수를 사용하여 총 24가지를 사용하였는데, 중심축에 따른 난류유동 측정을 통하여 두 프랙탈타입의 형상변수에 따라 난류강도의 경향이 달리 나타나는 것을 확인하였고, 형상변수에 따른 난류의 의존성을 정량화하기 위해서 각 프랙탈타입은 개별적으로 평가하였다. 또한 중심축을 따라 취득된 데이터가 화염이 실제로 존재하게 될 영역의 난류강도를 나타낼 척도가 될 수 있는지 확인하고자 화염이 존재하게 될 영역( mm)의 난류강도 평균값과 중심축(, mm)의 난류강도 평균값을 비교하였다. 결과적으로 크로스타입의 경우 최대 16%, 스퀘어타입의 경우 최대 45%의 상대오차를 가지며 이 차이는 유동장의 비균질성으로 인해 생성된 것으로 판단하였다. 이러한 조사를 통하여 중심축 평균 난류강도인 가 5% 이하인 스퀘어타입 프랙탈 조건을 제외하고 난류특성은 중심축 값으로 잘 표현할 수 있다고 하였다. 하지만 이러한 결과는 난류강도 비균질성의 결과값만 보여주고 있어 평균속도 및 속도섭동도 함께 조사하여 이러한 비균질성이 나타나는 이유를 파악할 필요가 있음을 보였다.
이처럼 난류화염을 조사하기 전 선행 작업으로 비반응장 난류특성을 다양하게 조사하고 있지만 일반타공판 대비 프랙탈타입의 난류 증대 효과가 명확하지 않고, 특히 프랙탈 형상의 난류생성판을 사용하기 위해선 프랙탈 형상매개변수에 따른 난류유동 및 비균질성에 대한 체계적인 연구가 추가적으로 이루어져야 한다고 판단되었다. 그리고 기존 연구들은 모두 사각 덕트 내에서 프랙탈 난류생성판을 조사하였지만 원형 덕트에 맞는 프랙탈 난류생성판의 난류 유동 특성은 아직 보고된 바가 없다.
본 연구에서는 V-shape 화염을 이용한 원형 프랙탈 난류생성판의 난류화염구조와 및 난류연소속도를 조사하기 앞서 난류화염에 직접적으로 영향을 미치는 비반응장 유동의 특성을 전반적으로 파악하고 난류화 정도를 기존에 사용되고 있는 일반매쉬 및 타공판과 함께 평가하였다. 이러한 분석은 이전 연구들에서 미흡했던 타공판 대비 프랙탈 난류생성판의 난류증대 효과 및 비균질성에 대한 설명뿐 만 아니라 다음 Part에서 계속 보고될 난류화염의 구조 및 Flame brush 특성과 난류연소속도에 대한 결과를 이해하는 통찰력을 제공한다. 또한 원형 프랙탈 난류생성판을 사용하는 본 연구의 결과는 저선회 연소기에 직접 적용이 가능하며 저선회 연소의 전반적인 특성을 이해하는데 큰 도움이 될 수 있다.
논문은 다음과 같이 구성되어 있다. 먼저 V-shape 버너 장치와 난류생성판으로 선정된 두 종류(스퀘어, 크로스) 타입의 프랙탈 구조를 결정하는 형상매개변수를 설명하고, 비반응 유동장 특징을 분석하기 위한 실험방법 및 분석절차, 실험조건에 대해 기술한다. 그 후 난류 예혼합화염에 직접적으로 영향을 미치는 난류유동장의 특징을 평가하고자, 비반응장에서 중심 축에 따른 난류특성을 정성적으로 경향을 설명하고, 기존에 널리 사용되고 있는 일반매쉬 및 타공판 그리고 프랙탈 난류생성판의 차이를 통계적으로 비교해 본다. 또한 화염이 존재하게 될 영역 (r, z)의 2D 평면 측정을 통하여 각각의 프랙탈 격자에서 생성된 유동장 비균질성을 정성적으로 평가하고, Verbeek[14]의 연구결과와 유사한 방법을 이용하여 기존에 잘 알려진 방법인 중심축에 따른 난류유동 측정방법과 (r, z) 평면 측정법의 차이 정도를 확인한다.
2. 실험장치 및 방법
2.1 V-shape 버너
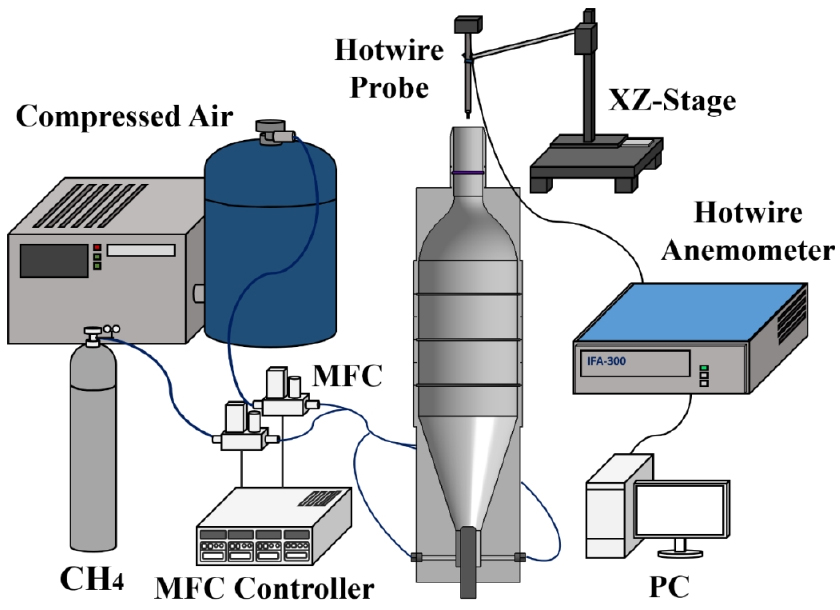
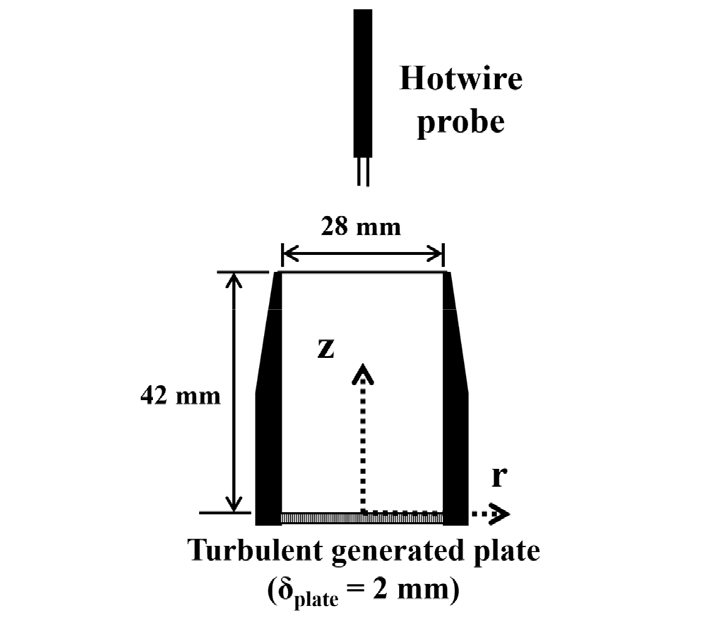
원형 난류생성판의 난류유동 특성 및 난류화염의 구조, 난류연소속도를 평가하고자 얇은 원형 봉-막대를 이용한 예혼합 V-shape 화염 실험장치에서 화염 안정화를 위한 봉-막대가 없는 원형풍동의 버너와 비반응장을 조사하기 위한 실험장치 개략도를 Fig. 1에 나타내었다. 버너풍동은 균일한 유동을 생성하기 위하여 긴 아크릴 원통형 파이프 사이사이에 정류격자 역할을 하는 얇은 매쉬와 난류생성판 하단에 약 13의 교축비를 가지는 헬름홀츠 형상으로 제작하였다. 노즐출구 직경인 는 28 mm, 난류생성판과 노즐출구까지의 거리인 은 42 mm 로 고정하였고 노즐출구 부근의 개략도는 Fig. 2에서 확인할 수 있다. 이 경우 노즐출구까지의 거리는 웨이크 상호작용(wake interaction) 이론[12]을 참고하여 다양한 난류 스케일의 상호작용으로 난류강도가 증가하는 난류 발달영역을 지나 모든 실험조건이 난류 붕괴영역에서 화염이 존재하도록 하기위해 선정되었다(난류발달영역 및 난류 붕괴영역에 대한 자세한 내용은 2.4절에서 설명된다). 이는 최대 난류강도 이전인 난류 발달영역에서 화염이 존재하게 구성되면 화염날림(blow out)과 역화현상등으로 화염을 안정화시킬 수 없음을 사전 예비실험을 통해 확인하였다. 프랙탈 형상매개변수에 따른 비반응장의 난류유동 특징을 확인하기 위하여 공기만을 사용하였고 체적유량 기반의 출구속도(bulk velocity, )는 4 m/s로 고정하였다. 이 체적유량은 dry gas meter(shinagawa, DS-16A-T)로 보정한 MFC(Line tech, Air, max. 300 SPM)와 MFC Controller(MKP, MPR 3000S, 4-ch)를 NI 기반 Lab-view 프로그램을 이용하여 제어하였다.
2.2 프랙탈 형상의 난류생성판
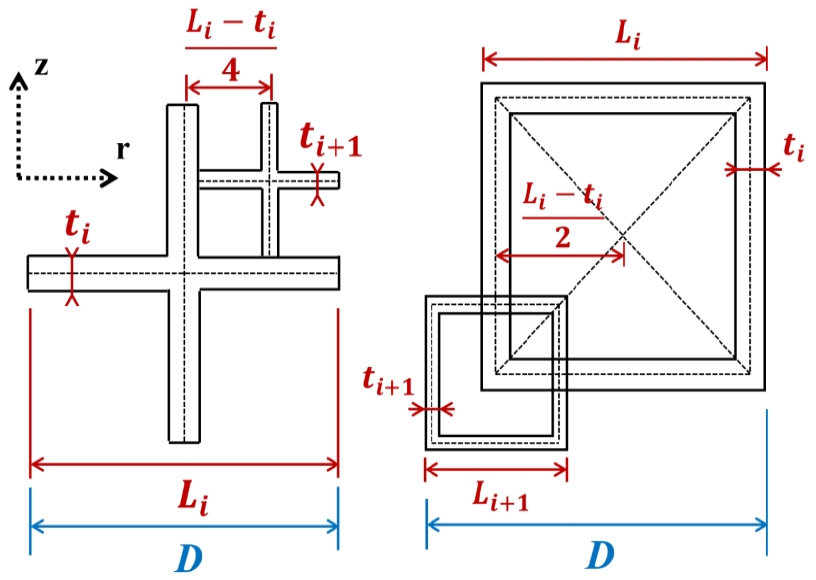
프랙탈 형상을 갖는 난류생성판의 종류로는 크로스, 스퀘어타입, 그리고 일반격자와 비교하기 위하여 타공판 타입(Hexa Type, 이하 헥사타입)등 3종류로 선정하였다. 크로스타입은 Hurst, Vassilicos의 제작방법에서 조금 수정된 Verbeek[14]의 형상을 참고하였고, 스퀘어타입은 기존 Hurst, Vassilicos[12]의 제작방법과 동일하게 하였다. 그리고 일반타공판은 본 연구팀의 이전 연구에서 사용한 헥사타입의 형상과 패턴을 참고하였다[10], [11], [15]. 프랙탈 격자인 크로스 및 스퀘어타입의 경우 동일한 형상매개변수가 적용되는데, (1) 프랙탈 반복횟수(number of fractal iteration) 과 막힘률(, blockage ratio), (2) 정해진 반복횟수에서 막대의 두께감소비율(, reduction rate of bar thickness), (3) 초기 형상(제일 큰 막대 구조)의 길이()와 두께()등과 같은 형상매개변수를 선택하면 특정 패턴을 가지는 프랙탈 격자가 완성되며 이와 관련된 자세한 형상은 Fig. 3에서 확인할 수 있다. 로 정의되는 막힘률에서 는 원형 노즐의 면적으로 , 는 난류생성판의 형상이 차지하는 면적이다.
본 연구에서는 반복횟수를 으로 고정하였고 과 를 주요 형상매개변수로 설정하였다. 원형노즐에 장착하기 위하여 완성된 프랙탈 격자 중 노즐 출구면적을 제외한 나머지 바깥 영역은 제외된다. 이때 원형 버너에 고정하기 위하여 링 영역을 추가적으로 제작하였고, 이러한 링 영역은 실제 유동 흐름에는 영향을 미치지 않으며 프랙탈 패턴의 구조만으로 난류유동을 발생시키게 된다. 원형 프랙탈 격자인 경우 도면 생성 전에 을 미리 예측할 수 없기 때문에 , 를 변경하여 원하는 막힘률을 시행착오 방법으로 찾았으며, 이때 난류생성판의 막힘률 오차는 0.01% 이내였다.
프랙탈 격자 중 크로스타입의 는 구조 특성상 가 자동으로 충족되지만, 스퀘어타입은 프랙탈 패턴의 중심에서부터 3번째 반복된 격자의 두께인 에 해당하는 마지막 구조까지의 길이가 를 만족해야 하는 것을 고려하면[12]와 는 다음의 식 (1)으로 표현할 수 있다.
이때, 는 노즐출구 직경이다. 과 을 식 (1)에 적용하면,
로 표현 할 수 있다. 는 형상매개변수로 아는 값이고 스퀘어타입의 막대두께감소비율(, reduction rate of bar length)이 임을 고려하면 와 에 대한 식으로 다음과 같게 된다.
식 (3)을 통하여 노즐출구의 직경 와 주요 형상매개변수인 , 를 적용하게 되면 의 값은 간단히 구할 수 있고, 이 값은 실제 도면을 제작할 시 유용하게 사용하게 된다. 모든 난류생성판은 CATIA V5R20 프로그램을 사용하여 설계하였고, 3D 프린팅 기술을 이용하여 SUS-316A 재질로 제작하였다. 이때 3D 프린트의 최소 제작가능 두께는 0.25 mm이며 분말 상태나 기타 공정조건에 따라서 적층방향으로 0.03 - 0.05 mm, 레이저 조사방향으로 0.1 mm의 오차를 가진다.
2.3 열선유속계
비반응장의 난류유동에 대한 정량적인 데이터는 정밀 열선유속계(Hot-wire anemometry) 시스템을 사용하여 측정하였다. 축 방향 및 반경 방향 속도측정이 가능한 2채널 프로브 센서와 프로브, TSI IFA-300 CTA 모듈로 이루어져 있으며, 취득된 데이터는 TSI Thermo pro 프로그램을 통해 저장된다. 속도에 대한 정보는 공급유량을 고려하여 1,000 Hz, 16 sec 동안 측정하였고, 20 kHz, 180 sec 동안 측정한 데이터와 0.1% 이내로 차이나는 것을 확인하였다. 측정된 모든 데이터는 Matlab R2020a로 변환, 분석하였다.
2.4 실험조건 및 버너의 난류 정보
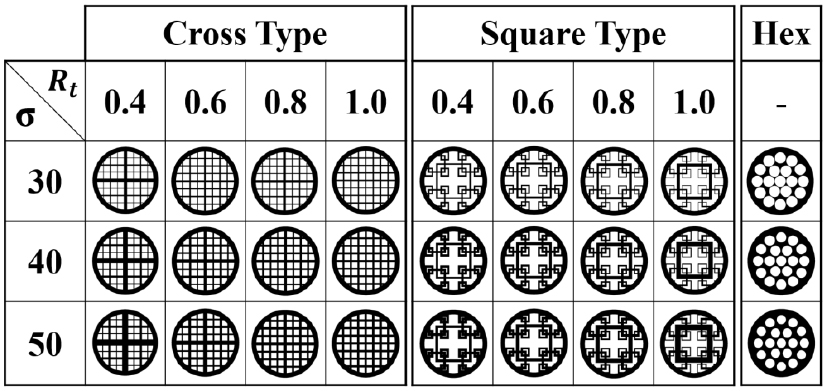
본 연구에서 사용한 난류생성판의 형상들을 Fig. 4에 나타내었고 사용한 프랙탈 형상의 기본적인 구조 정보는 Table 1에서 확인할 수 있다. 크로스와 스퀘어타입의 격자는 막대두께 감소비율인 와 막힘률인 를 변경하여, = 0.4, 0.6, 0.8, 1.0, = 30, 40, 50%로 총 24 가지를 사용한다. 그리고 비교를 위해 일반타공판 형상인 헥사타입의 격자는 프랙탈타입의 막힘률과 동일한 = 30, 40, 50% 3가지이다. = 50%는 응용을 위한 실제 저선회 연소기에서 사용하는 = 65 - 80% 보다는 비록 낮은 막힘률이지만 [10], [11], [15], 스퀘어 프랙탈의 구조중첩 문제[14], 강한 난류강도와 희박한 당량비에 의한 화염날림 현상으로 인하여 = 50%까지로 제한하였다.
Table 1.
Overview of shape parameters and flow data for each turbulence generator type. The flow values are the center data of the bottom of the flame stabilization rod (r = 0 mm, z = 45 mm) to be used next paper(Part II)
Table 1의 표현에서 “Name”에 해당되는 기호의미를 설명하자면 C30_0.4는 크로스타입의 = 30%, = 0.4를, S는 스퀘어타입을 의미한다. 여기서 크로스타입의 = 1.0은 프랙탈 패턴의 모든 두께가 동일하며 이는 일반적으로 사용하는 Mesh의 형태와 유사하여 타공판과 같이 비교 대상으로 사용하였다. 는 Vassilicos가 제안한 스퀘어타입의 웨이크 상호작용 길이(wake interaction length scale)로 으로 계산되며, 도 Vassilicos가 제안한 프랙탈 격자의 유효 매쉬 크기(effective mesh size)로 일반 매쉬 크기(mesh size)와 비교하고자 프랙탈의 경계 길이 와 풍동 단면적 의 비율, 막힘률을 사용하여 로 나타낸 형상정보이며, 본 연구에서는 원형노즐임을 고려하게 되면 로 표현된다[12].
본 연구에서 조사한 난류생성판의 난류유동 정보도 Table 1에 나타내었다. Table 1에 제공된 수치들은 노즐출구 기준 3 mm 떨어진 곳에서 취득한 중심축 데이터(z = 45 mm, r = 0 mm)이며, 이는 나중에 화염을 안정화하기 위한 막대(rod) 하단 위치에 해당한다(즉, = 46 mm). , 는 레이놀즈 분해(Reynolds decomposition) 방법을 이용하여 얻었으며[1], 얻어진 시간별 데이터는 식 (4)로 나타낼 수 있다.
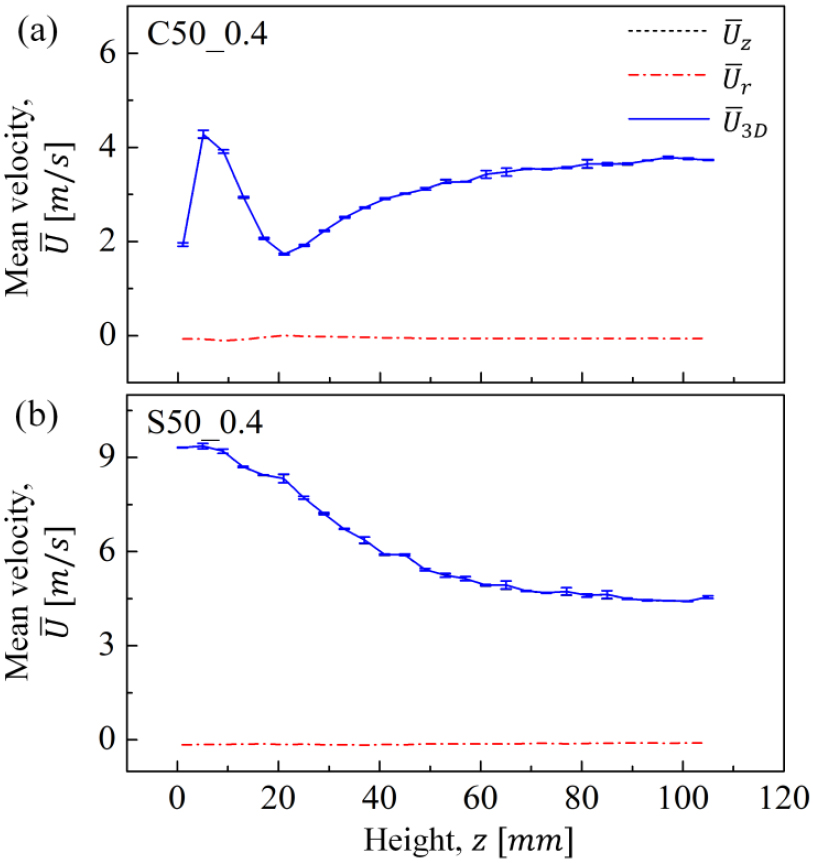
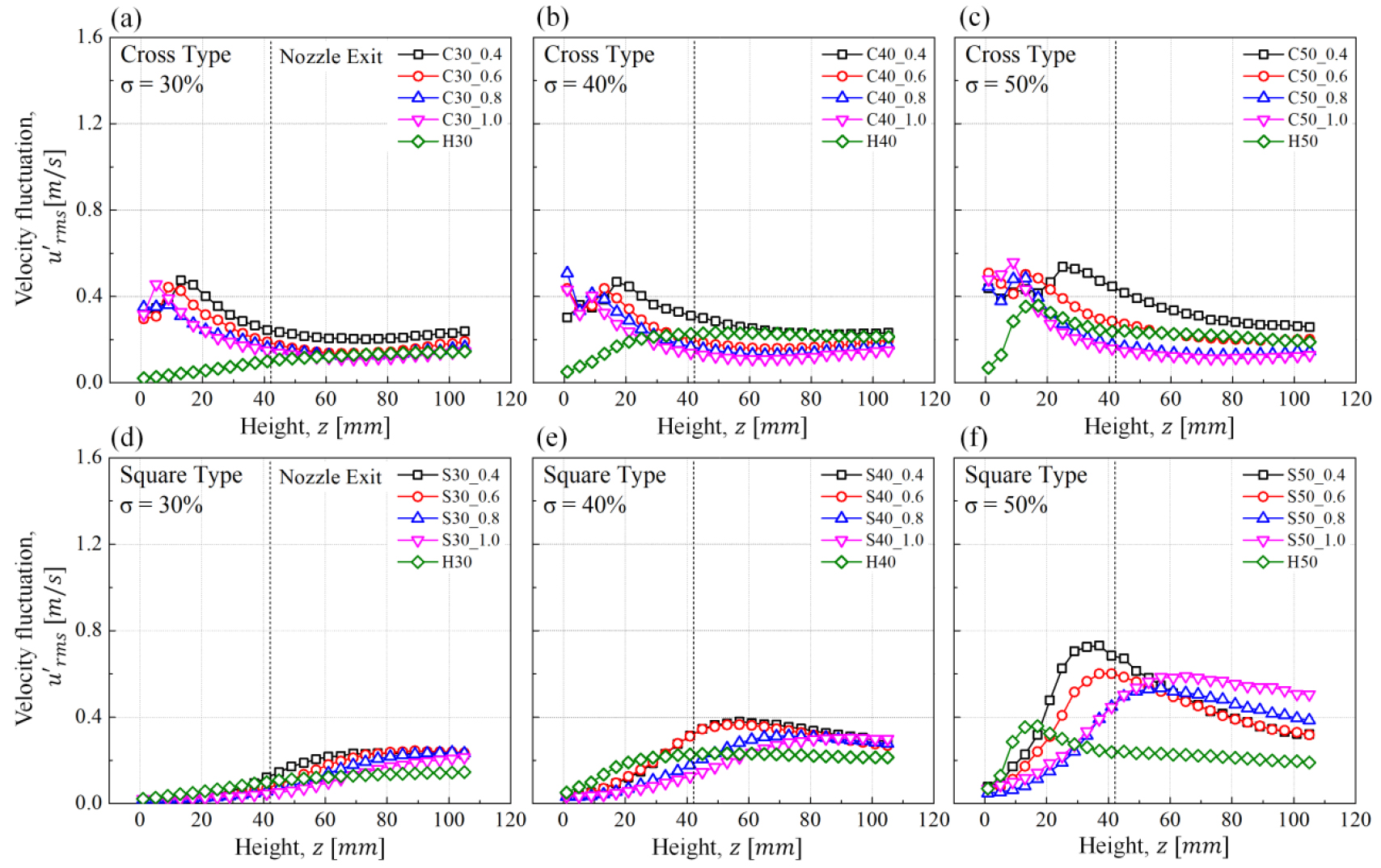
이때 는 측정시간의 평균속도이며, 은 해당시간의 속도섭동이다. 이 경우 속도섭동분의 크기를 나타내기 위하여 을 rms 값을 취하였으며, 이를 속도섭동 로 사용하였다. 중심축을 따라서 측정된 축 방향 및 반경 방향의 평균속도를 Fig. 5에 나타내었다. 대표적인 두 조건(C50_0.4, S50_0.4) 모두 축 방향의 평균속도()는 속도분포의 차이가 난류생성판에서 떨어진 높이에 따라 뚜렷했지만 반경방향의 평균속도()는 모든 높이에서 0 근처의 값을 갖는 것을 알 수 있다(즉, ). 이는 버너설계 특성상 전체 유동이 축 방향으로 흐르기 때문에 난류생성판 이후에 난류유동이 존재하더라도 은 매우 작은 값임을 알 수 있고, 이를 고려하여 본 연구에서 나타낸 평균속도 는 의 값을 사용하였다. 그러나 동일한 실험조건에서 속도섭동의 결과 값은 와 의 값이 모두 존재하는 것을 알 수 있다. 따라서 총 속도섭동 는 식 (5)를 이용하여 구하였다.
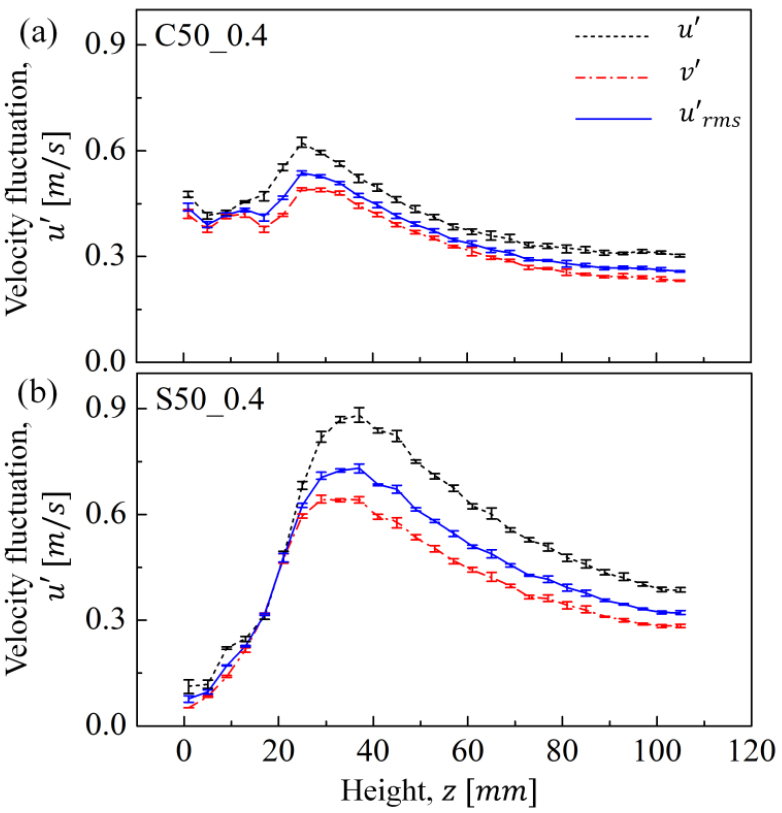
난류생성판과 버너 모두 중심축 기준으로 대칭을 이루고 있고 유동 방향이 정해져 있기 때문에 와 는 같다고 가정하였고 식 (5)의 결과 값을 Fig. 6에 나타내었다. 대개 축방향의 속도섭동 를 속도섭동 대표 값으로 사용하는 다른 저자들도 있어 다소 혼동이 있을 수 있지만 Fig. 6에서 확인할 수 있듯이 높이에 따른 속도섭동의 경향은 매우 유사하다. 이때 두 그래프에서 는 점점 증가하다가 최고점을 지나 다시 낮아지는 것으로 관찰되는데 이러한 현상을 구분하기 위하여 속도섭동, 즉 난류에너지가 증가하는 구간을 ‘난류 발달영역’, 최대 속도섭동 이후에 난류가 소산되어 가 점점 줄어드는 구간을 ‘난류 붕괴영역‘이라 정의하였다. 이때 Fig. 5, 6에 나타낸 오차막대(error bar)는 취득된 데이터를 2 sec씩 나누어 변환한 결과와의 차이를 보여준다. 평균속도 및 속도섭동의 결과 모두 차이가 거의 없었으며, 동일한 방법으로 본 연구에 나타낸 모든 결과값은 2.8% 이내의 작은 오차를 가지는 것을 확인하였다. 국부난류강도(local turbulent intensity) 는 로 산출하였으며, 해당 영역에서 평균속도와 속도섭동의 크기를 비교할 수 있는 지표이다.
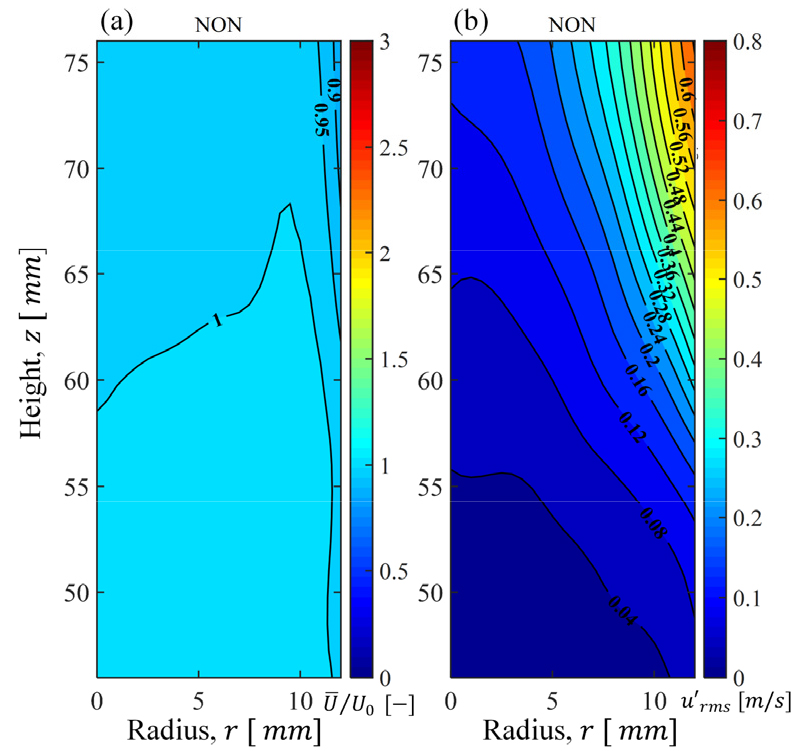
다음으로 난류생성판이 없는 버너의 비반응장 결과값을 Fig. 7에 나타내었다. 무차원화 된 평균속도인 Fig. 7(a)의 은 전체적으로 1.0으로 유사하게 분포하는 것을 알 수 있고, 이는 버너 형상 및 매쉬에 의한 에너지 손실이 매우 작다는 것과 노즐출구에서 균일한 유동이 형성됨을 보여준다. Fig. 7(b)인 의 경우 z = 60 - 76 mm, r = 12 mm 부근에서 유독 큰 값이 나타났는데, 이는 전단층(share layer)에 대한 영향과 헬름홀츠(Helmholtz) 형상으로 인해 제트 바깥의 양 옆에 한 쌍의 와류가 생성되는 헬름홀츠 형상의 고유주파수 영향임을 사전에 확인하였고 이러한 현상은 난류생성판이 존재하는 조건에서는 관찰되지 않았다.
3. 결과 및 고찰
3.1 중심축에 따른 난류특성
노즐의 중심축을 기준으로 난류성분을 취득하는 방법은 축을 기준으로 대칭인 난류생성판에서 난류유동의 특징을 확인할 수 있는 좋은 수단으로, 이전 연구들에서 자주 사용하는 방법이다[12], [13], [14]. 본 연구에서도 동일한 방법으로 화염에 직접적으로 영향을 미치는 난류유동이 어떻게 발달하고 소멸하는지 확인하기 위해 난류생성판 부근에서부터 화염이 존재하게 되는 높이까지 중심축을 따라 측정하였다( = 1 - 108 mm).
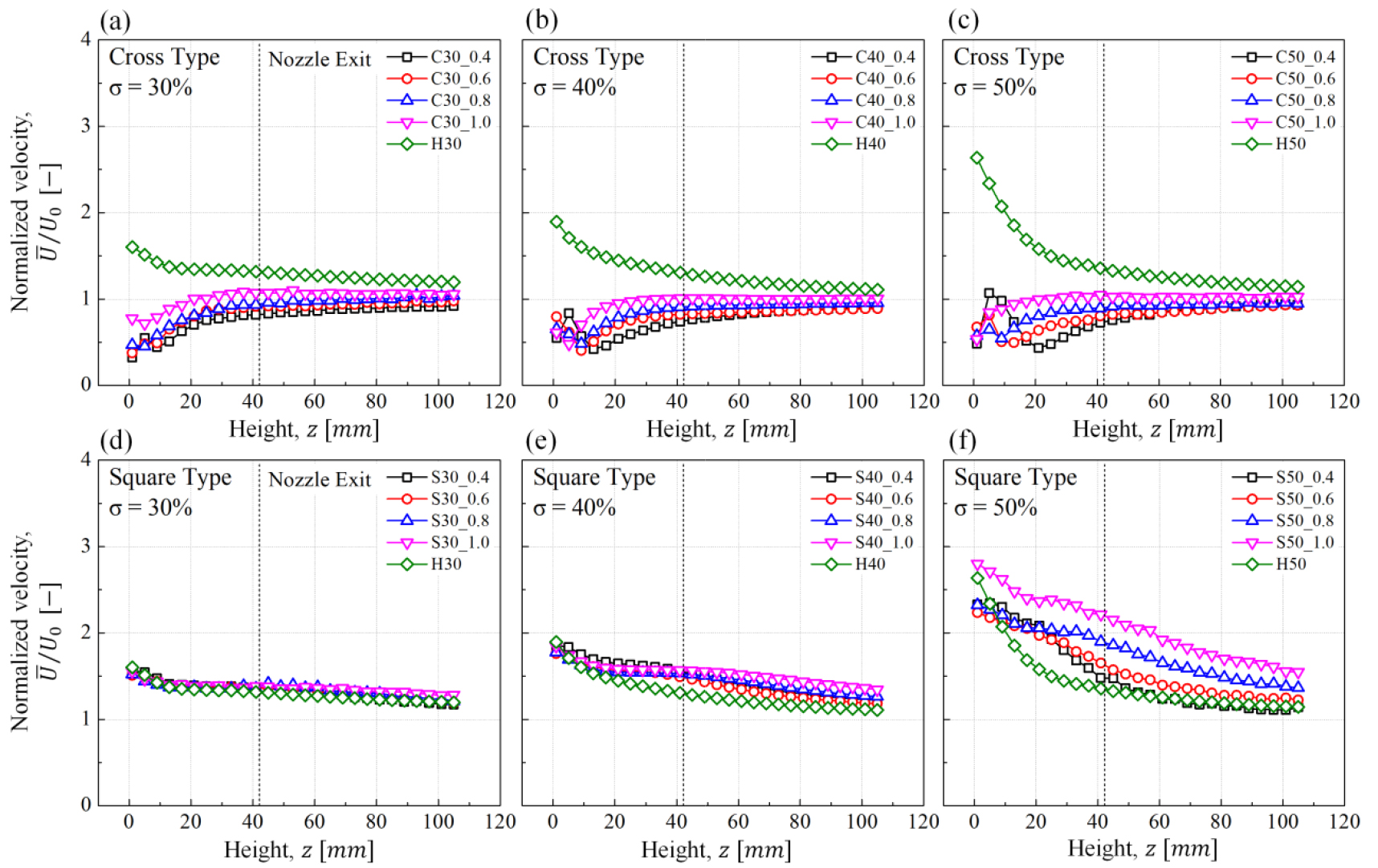
우선 본 연구에서 사용한 프랙탈타입의 격자와 일반타공판인 헥사타입 격자의 중심축 난류성분들 중 를 Fig. 8에 나타내었다. 전체적으로 크로스 격자의 경우 중심에 가장 큰 두께인 에 해당하는 격자부분이 존재하여 난류생성판 부근에서의 는 보다 낮지만 높이가 증가함에 따라 = 1.0 근처로 수렴된다. 또한 이 증가하거나 가 감소하면 평균속도 최저점이 나타나는 높이가 증가하며 이는 중심축에 존재하는 격자부분의 두께인 가 증가하여 나타난 결과로 유추할 수 있다. 이에 비해 스퀘어타입과 헥사타입의 경우 가운데에 프랙탈 구조가 존재하지 않아 평균속도가 프랙탈 부근에서 제일 높고 이후 점점 낮아지면서 = 1.0에 가까워진다. 이러한 경향은 이 증가할수록 뚜렷하게 나타났으며, 이는 이 높아짐에 따라 유량이 흐르는 면적이 작아져 난류생성판 중 열려있는 구간에 유량이 집중되고 속도가 증가하여 생긴 현상으로 알 수 있고, 일정 높이(평균속도 최저점) 이후에서는 난류에너지가 다시 소산되어 평균속도의 값이 일부 복구되어 = 1에 가까워지는 것으로 판단된다.
다음은 두 가지 타입의 프랙탈격자와 일반격자의 중심축 속도섭동인 을 Fig. 9에 나타내었다. 두 프랙탈타입과 헥사타입 모두 동일하게, 이 증가하거나 가 낮아지면 최대 속도섭동과 그 이후의 후류지점의 속도섭동이 증가하였다. 이 중 에 따른 속도섭동의 변화 폭은 크로스타입보다 스퀘어타입이 더 높게 관찰된다. 명확한 차이점은, 크로스타입에서 이 증가하고 가 낮아지면 최대 속도섭동이 나타나는 높이가 점점 후류지점으로 밀려나 난류 발달영역이 증가하는 반면 스퀘어 프랙탈의 경우 오히려 최대 속도섭동의 높이가 난류생성판 부근으로 가까워져 난류 발달영역이 감소하는 것을 볼 수 있다. 즉, 최대 속도섭동의 변화율, 최대 속도섭동이 나타나는 지점이 두 프랙탈타입의 과 에 따라 서로 다른 경향을 보이며, 이러한 두 프랙탈타입의 차이는 프랙탈의 복잡한 구조로 인하여 생성된 다양한 스케일의 와류가 서로 상호작용하는 영역 또는 높이가 주요 형상변수의 변경에 따라 다르게 작용하여 서로 상반된 경향이 나타나는 것으로 판단되며, 이를 참고하여 프랙탈 구조의 형상변수에 따라 난류강도 및 난류연소속도의 특징을 조사할 경우 두 프랙탈타입은 개별적으로 평가되어야 함을 알 수 있었다.
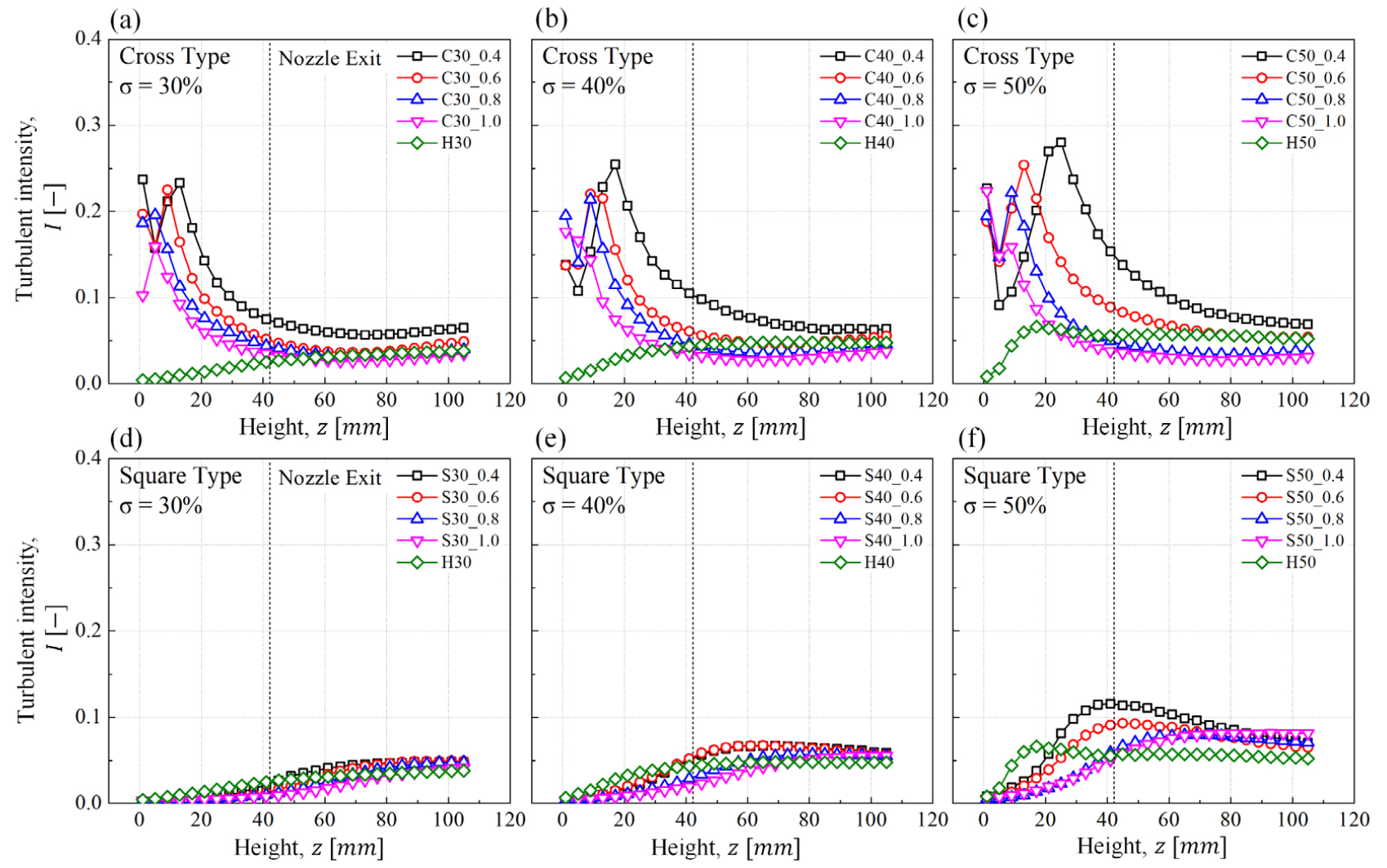
프랙탈 격자들에 대한 중심축에 따른 난류강도 를 Fig. 10에 나타내었다. 먼저 크로스타입인 경우 모든 조건에서 난류강도가 전체적으로 하나의 최대값으로 존재하는 것을 명확하게 확인할 수 있으며, 이 위치는 속도섭동의 최고점 또는 평균속도의 최저점과 매우 유사하였다. 두 프랙탈타입 모두 속도섭동의 경향과 동일하게 나타났지만 한 가지 차이점은 스퀘어타입이 더 높았던 속도섭동 결과 값과(예를 들어 Fig. 9의 = 50%)는 다르게 난류강도는 크로스타입이 더 높은 것으로 확인되었다. 이는 Fig. 8의 평균속도 분포()에서 확인할 수 있듯이 스퀘어타입의 평균속도()가 전체적으로 높아 국부적인 난류강도의 값은 작은 것으로 나타났다. 이처럼 중심축에 따른 속도 데이터의 분석은 해당 난류생성판의 난류화 정도를 확인하고 두 프랙탈 난류생성판의 주요 형상매개변수에 따른 난류유동의 특징도 직접적으로 설명이 가능하였다. 또한 이러한 정보는 수치해석 결과값과 실험데이터를 비교할 때에도 유용하다.
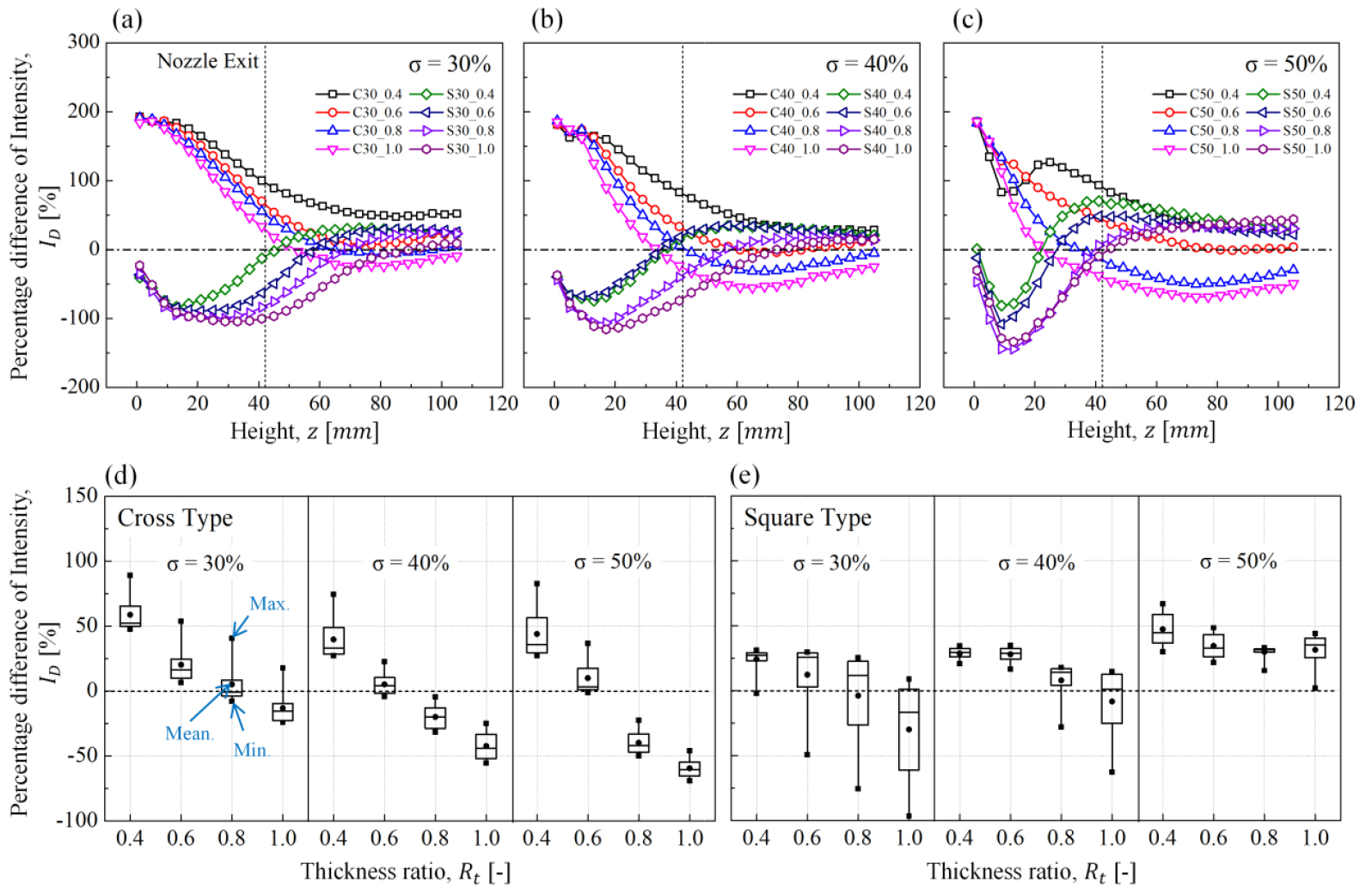
다음으로 프랙탈타입과 헥사타입의 난류강도의 차이를 정량적으로 평가하기 위하여 Fig. 11에 나타내었다. 이 때 사용한 는 난류강도의 백분율오차(percentage different of intensity)이며 식 (6)을 이용하였다.
여기서 는 비교하게 되는 프랙탈타입의 난류강도이며 의 경우 참고하는 난류강도(reference Intensity)로 Fig. 11에 나타낸 은 비교할 프랙탈타입의 난류강도와 동일한 막힘률을 가지는 헥사타입의 난류강도 값을 사용하였다. 식 (6)이 의미하는 것은, 만약 < 0 의 경우, 해당 난류강도가 참고 값인 난류강도보다 비교적 낮고, > 0 은 해당 난류강도가 참고 난류강도보다 더 높다는 것을 의미한다.
크로스타입의 모든 조건에서는 프랙탈 부근()의 가 제일 높았으며 이와 반대로 스퀘어타입은 노즐출구 이전까지 대부분 < 0에 해당하였다(Fig. 11(a), (b), (c) 참고). 실제 난류 예혼합 화염이 존재하게 될 노즐출구 이후(z > 42 mm)에서는 대부분의 프랙탈 조건들이 > 0으로 프랙탈 형상의 난류강도가 더 강한 것을 알 수 있다. 하지만 그래프가 중첩되어 식별하는데 어려움이 있고, 노즐출구 이후에서의 를 정량적으로 비교하고자 상자그림방법(box-plot method)을 이용하여 Fig. 11(d), (e)에 나타내었다. 상자그림방법은 통계적으로 여러 정보를 한 눈에 볼 수 있는 방법으로 기호(symbol)를 통해 최대값, 최소값, 평균값을 확인할 수 있고, 네모 상자를 통해 25%, 50%, 75%의 백분위수를 한 눈에 볼 수 있다는 장점이 있다.
먼저 크로스타입의 경우 과 상관없이 가 낮아짐에 따라 최대값, 최소값, 평균값이 선형적으로 감소한다. 이는 Fig. 9의 설명과 동일하게 가 낮아짐에 따라 속도섭동이 감소하는 경향과 동일한 것을 의미한다. 스퀘어타입 중 = 30%는 가 증가하면 의 최대값과 최소값의 폭이 커지며, 이 증가할수록 그 폭이 줄어드는 것이 특징이다. 결과적으로 동일한 에서 형상매개변수를 조절하여 크로스 타입의 난류생성판은 헥사타입의 난류생성판보다 평균값 기준 난류강도를 최대 59%까지 증가하였으며(C30_0.4), 스퀘어타입의 난류생성판은 최대 47%까지 증가하는 것을 볼 수 있다(S50_0.4).
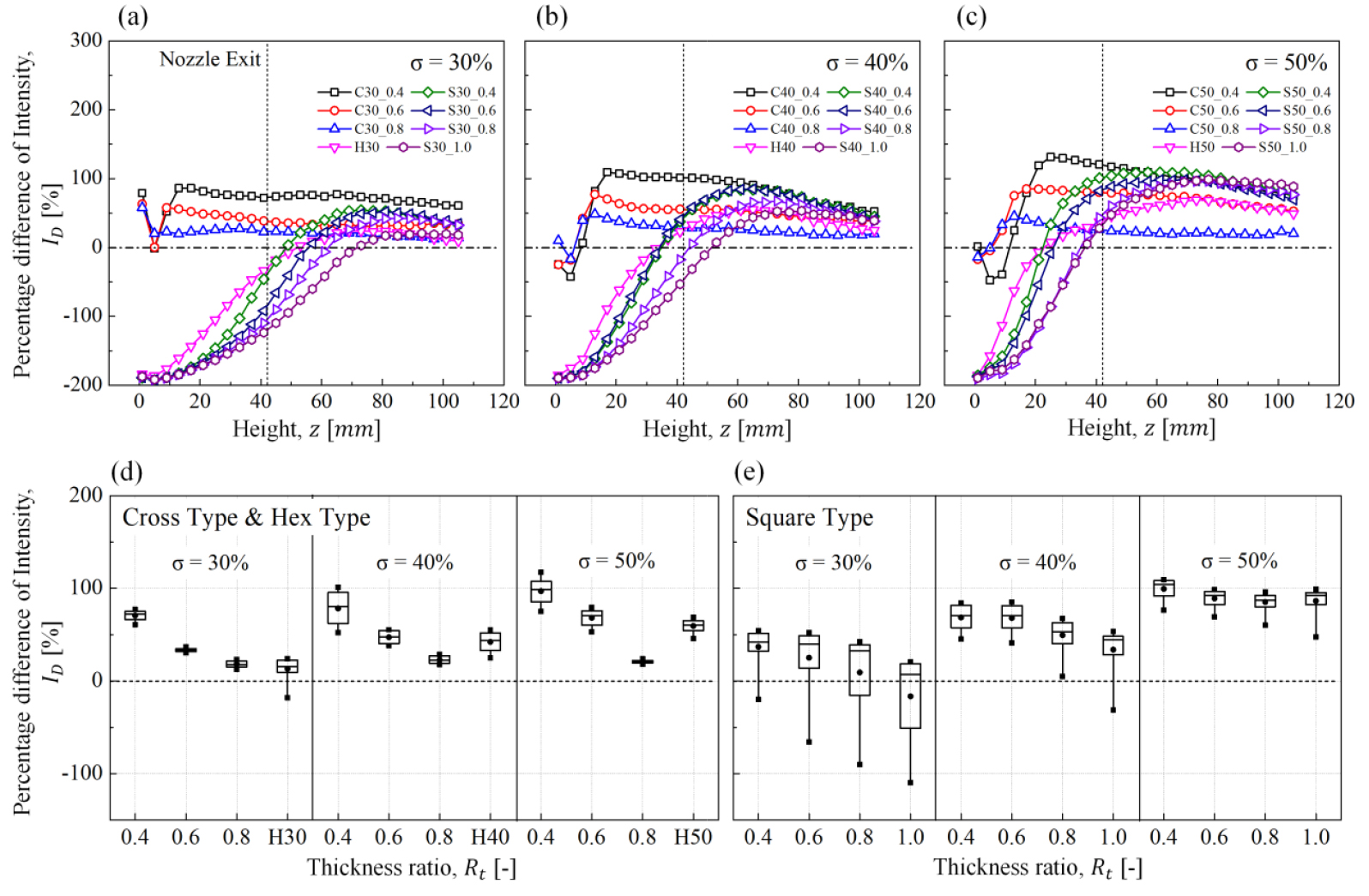
Fig. 12는 일반매쉬 형태와 유사한 크로스타입의 = 1.0과 프랙탈 형상의 난류생성판을 비교한 그래프로, 방법은 Fig. 11과 동일하게 식 (6)을 사용하였다. Fig. 12의 (a), (b), (c)에서 확인할 수 있듯이 스퀘어타입은 프랙탈 부근에서는 가 매우 낮고 높이에 따라 점점 증가하다가 노즐출구 이후부터는 양의 값을 가지는 것을 알 수 있다( > 0). 반면에 크로스타입의 경우 프랙탈 근처(z = 0 - 20 mm) 에서 는 하나의 최저점을 가지며 일정 높이 이상부터는 가 일정한 것을 알 수 있다. 이는 크로스타입의 난류생성판에서 생성된 난류유동이 최대 난류강도 지점 이후부터는 동일하게 난류강도가 줄어든다는 것을 의미한다. 두 타입의 프랙탈 조건은 노즐출구 이후부터는 대부분 양의 값을 갖고 있었고 이와 관련된 통계 그래프는 Fig. 12의 (d), (e) 그래프에서 자세히 확인할 수 있다. S30_0.4 조건을 제외하고 모든 난류생성판 조건이 평균값 기준 > 0을 만족하며, 이는 일반매쉬 형상의 난류생성판을 사용하는 것보다 프랙탈 형상의 난류생성판을 사용하면 더 높은 난류강도를 생성할 수 있다는 것을 보여주고 있다. 정리하자면 크로스타입의 난류생성판은 일반매쉬와 비교하여 난류강도가 평균값 기준 최대 97% 증가하였고(C50_0.4), 스퀘어타입의 난류생성판은 최대 99% 증가하였다(S50_0.4).
3.2 (r, z) 평면 유동장 특성
프랙탈의 난류생성판의 복잡한 형상으로 인하여 유동장의 비균질성(inhomogeneity)은 분명 존재하게 된다. 이러한 비균질성 또한 프랙탈의 형상매개변수에 따라 특정 경향이 나타날 것으로 판단되어 중심축 데이터가 과연 해당 난류생성판의 난류특성을 잘 나타내는지 확인하기 위하여 이에 대한 추가적인 조사를 하였다.
(r, z) 평면 유동장의 정보는 난류화염의 구조를 정성적으로 설명 및 이해하는데 도움이 될 뿐만 아니라, 일부 연구자들은 난류연소속도를 정의하는데 비반응장에서의 유동 정보를 가져오기도 한다[13], [14]. 모든 난류생성판은 축 기준 대칭을 이루고 있기 때문에 (r, z) 평면 유동장 등고선(contour)은 화염이 존재하는 노즐출구 이후와 외부유동의 영향이 적은 노즐직경 안쪽, 즉 z = 46 - 76 mm와 r = 0 - 12 mm에 해당하는 유동정보를 사용하여 파악하였다. 난류생성판의 반경 방향 축은 방위각(azimuth angle)축의 선정에 따라 평면 유동장 분포가 달라질 수 있기 때문에 반경 방향 축은 난류생성판 타입에 따라 기준을 정하였고 이는 Fig. 3의 좌표축과 동일하다.
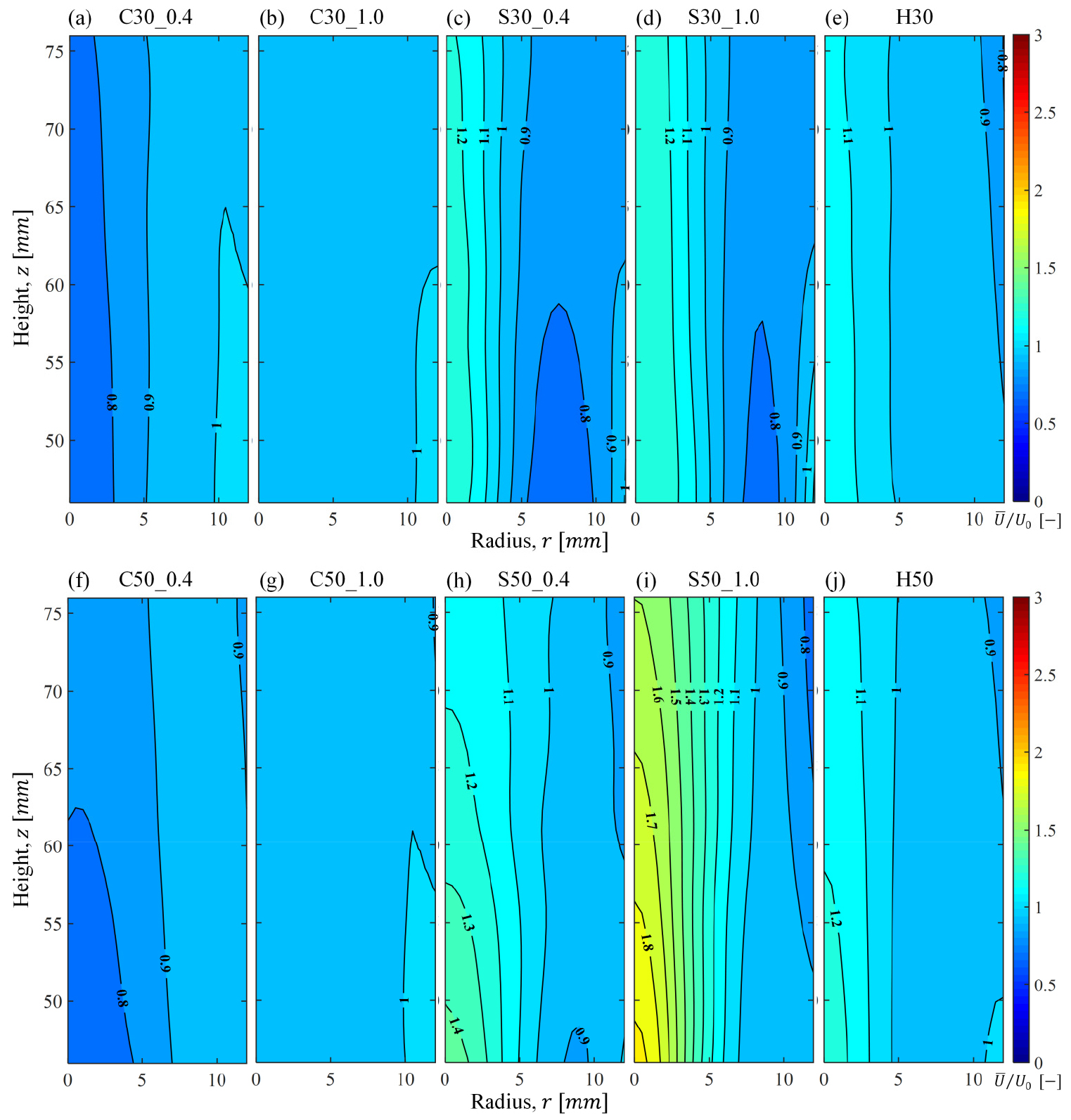
Fig. 13은 (r, z) 평면에서의 등고선 이미지를 보여주고 있다. 여기서 (a), (b), (f), (g)는 크로스타입의 평균속도 분포로 구조 특성상 중심축(r = 0)에 로 이루어진 십자(cross)형 격자가 존재하여 의 값이 1.0보다 낮았으며, 스퀘어타입인 (c), (d)는 중심축에 이러한 격자가 존재하지 않아서 평균속도가 1.0보다 더 높게 관찰되었다. 두 프랙탈타입은 공통적으로 축 방향 평균속도 구배는 적고 반경 방향의 속도 구배가 커 일정한 흐름선(stream line)을 형성하였다(). 이러한 반경 방향 속도 구배는 스퀘어타입이 비교적 더 명확하며, 이 증가할수록 반경방향의 평균속도 구배가 더 뚜렷해지는 것을 볼 수 있다. 결과적으로 프랙탈타입과 형상매개변수에 따라 평균속도는 주로 반경방향으로 비균질하며, 크로스타입보다 스퀘어타입이 더 비균질하다는 것을 보여준다.
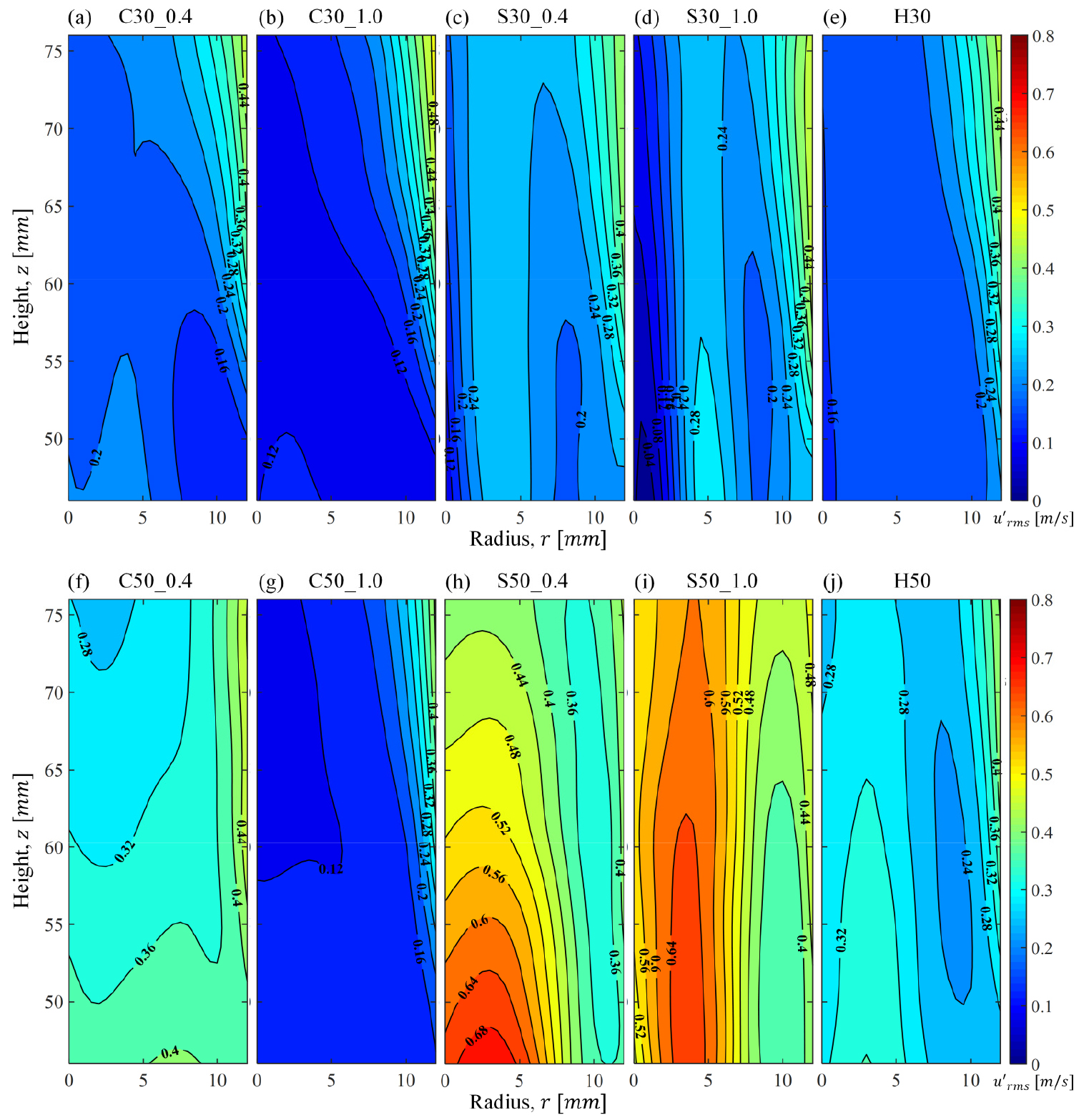
다음은 Fig. 13과 동일한 (r, z) 평면에서 속도섭동 의 분포 이미지를 Fig. 14에 나타내었다. 먼저, 모든 난류생성판에서 공통적으로 r = 12 mm, z = 66 - 76 mm에 해당하는 구간에서는 속도섭동이 일부 증가하는 것을 볼 수 있다. 이는 노즐출구 이후에서부터 발달한 전단층(share layer)에 의한 영향이며, Fig. 7에서 확인된 헬름홀츠 버너형상으로 인한 음향적 요소는 난류생성판을 사용할 때는 나타나지 않음을 사전에 확인하였다. = 30%의 난류생성판인 Fig. 14(a)-(e)는 속도섭동이 낮았으며, 이는 Fig. 9의 결과값에서 볼 수 있듯이 난류 발달영역이 짧아 최대 속도섭동 지점이 프랙탈 부근에서 생성되며, 난류의 확산이 주로 이루어지는 붕괴 영역을 지나는 시간()이 증가하여 노즐출구 이후(z = 42 mm)에서부터는 속도섭동이 비교적 작게 나타났다.
프랙탈타입 및 형상매개변수에 의한 속도섭동의 영향은 = 50%의 결과값인 Fig. 14(f)-(j)에서 명확하게 확인할 수 있다. 크로스타입(C50_0.4, C50_1.0)의 속도섭동 분포를 비교해보면 가 증가함에 따라 속도섭동은 최대 3 배 정도가 증가하는 것으로 관찰되며, C50_0.4의 은 반경방향보다 축방향의 구배가 더 크게 나타났다(). 이는 프랙탈 구조에 의한 유동장의 비균질한 것이 아닌 높이가 증가함에 따라서 난류의 소산으로 인하여 비균질해진 것으로 알 수 있다. 스퀘어타입(S50_04, S50_1.0)의 경우 공통적으로 크로스타입보다 더욱 심한 속도섭동이 관측됐으며, 속도섭동의 최대 지점이 중심축이 아닌 r = 3 - 5 mm 부근에서 나타난 것을 볼 수 있다. 이는 Fig. 4의 형상에서 볼 수 있듯이 에 해당하는 사각형 격자로 인해 생성된 큰 난류유동이 노즐출구 이후에까지 영향을 미치는 것으로 판단된다.
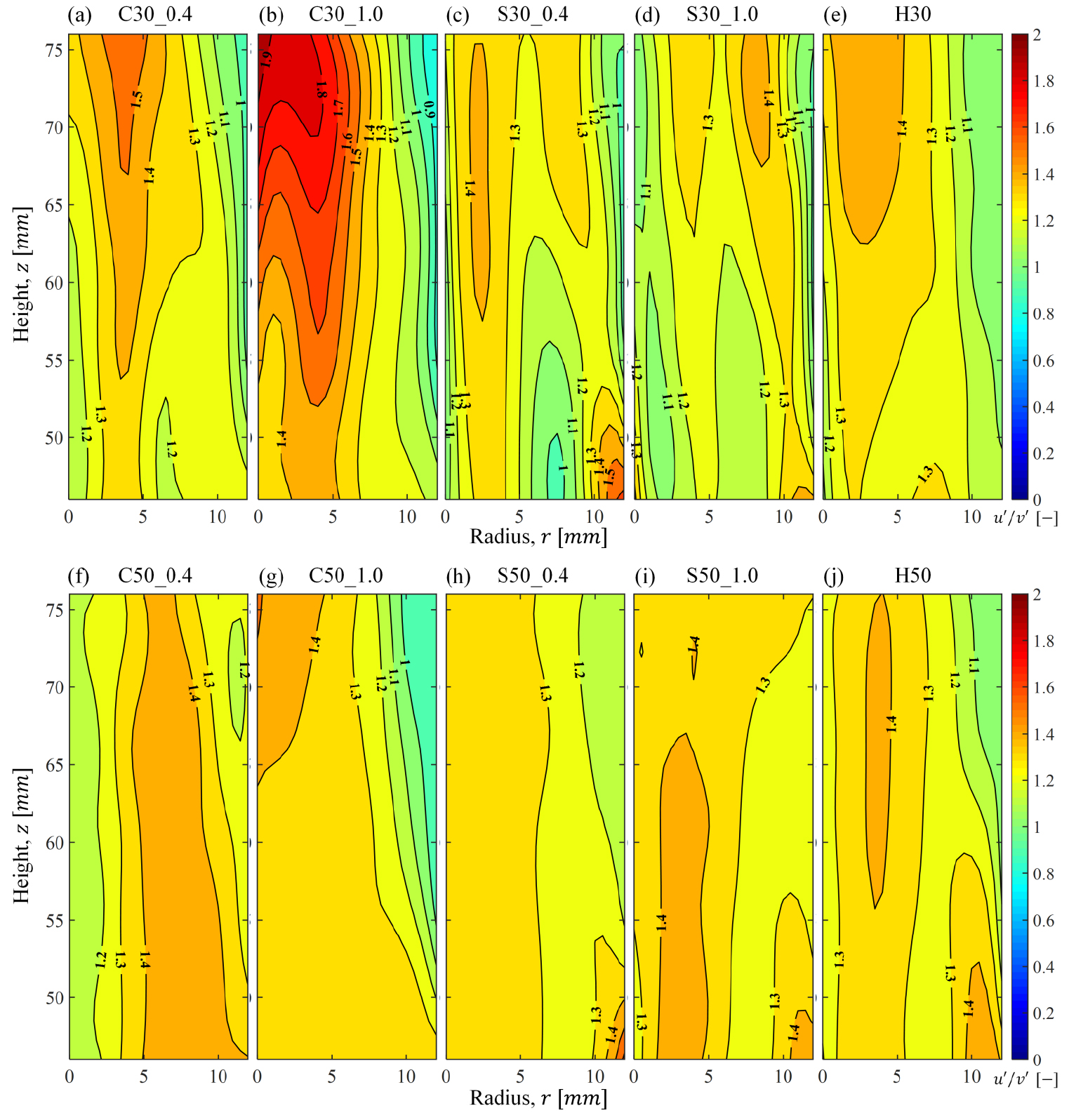
다음은 (r, z) 평면에서 난류의 등방향성 값인 의 결과값을 Fig. 15에 나타내었다. = 1이면 방향에 상관없이 동일한 속도섭동의 값을 나타내며 관측 방향과 무관하게 난류정보를 취득할 수 있다. 하지만 V-shape 버너는 구조적 특성상 z축 방향으로 유동이 흐르기 때문에 의 값이 1 - 1.5의 값을 유지하게 된다. 본 연구에서 모든 난류생성판은 대부분 = 1 - 1.5로 존재하였으나 C_30_10의 조건은 가 1.9까지 증가하는 것으로 나타났다.
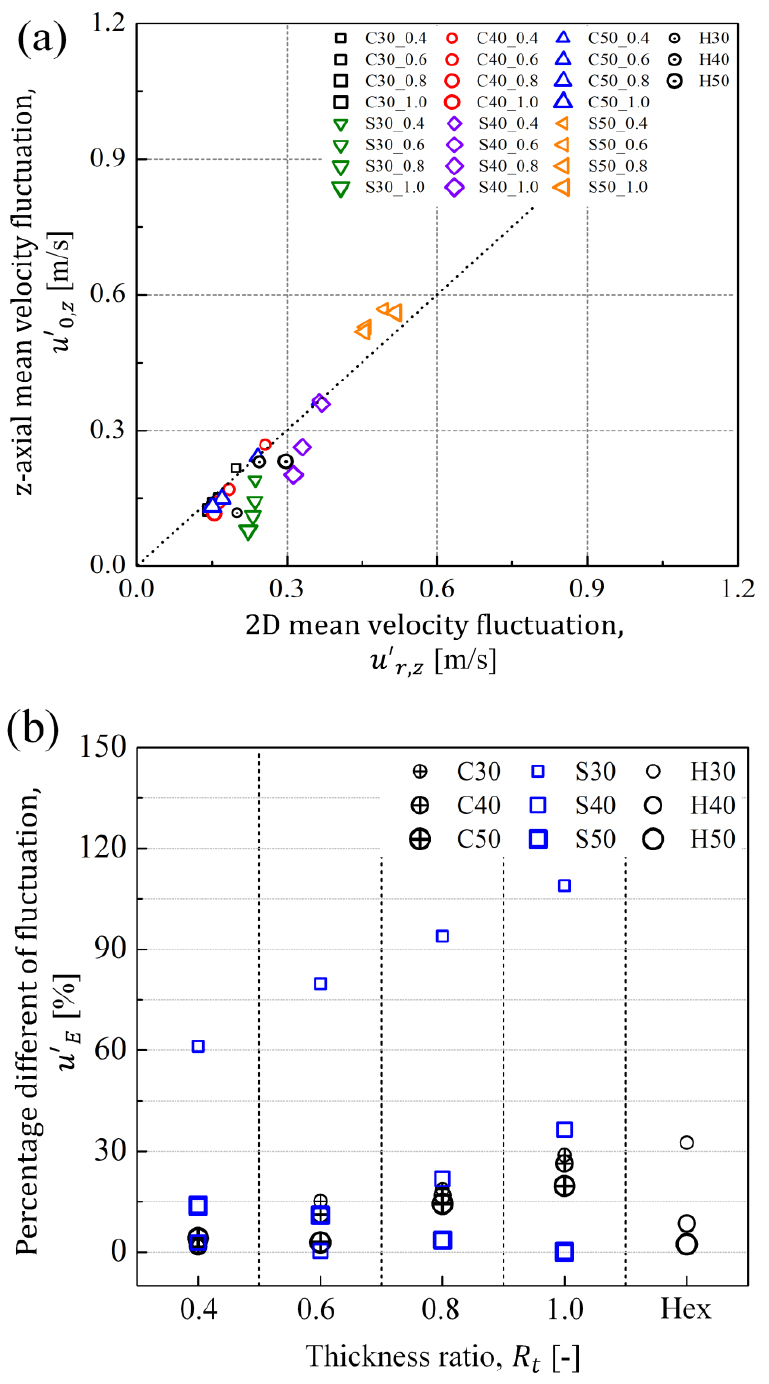
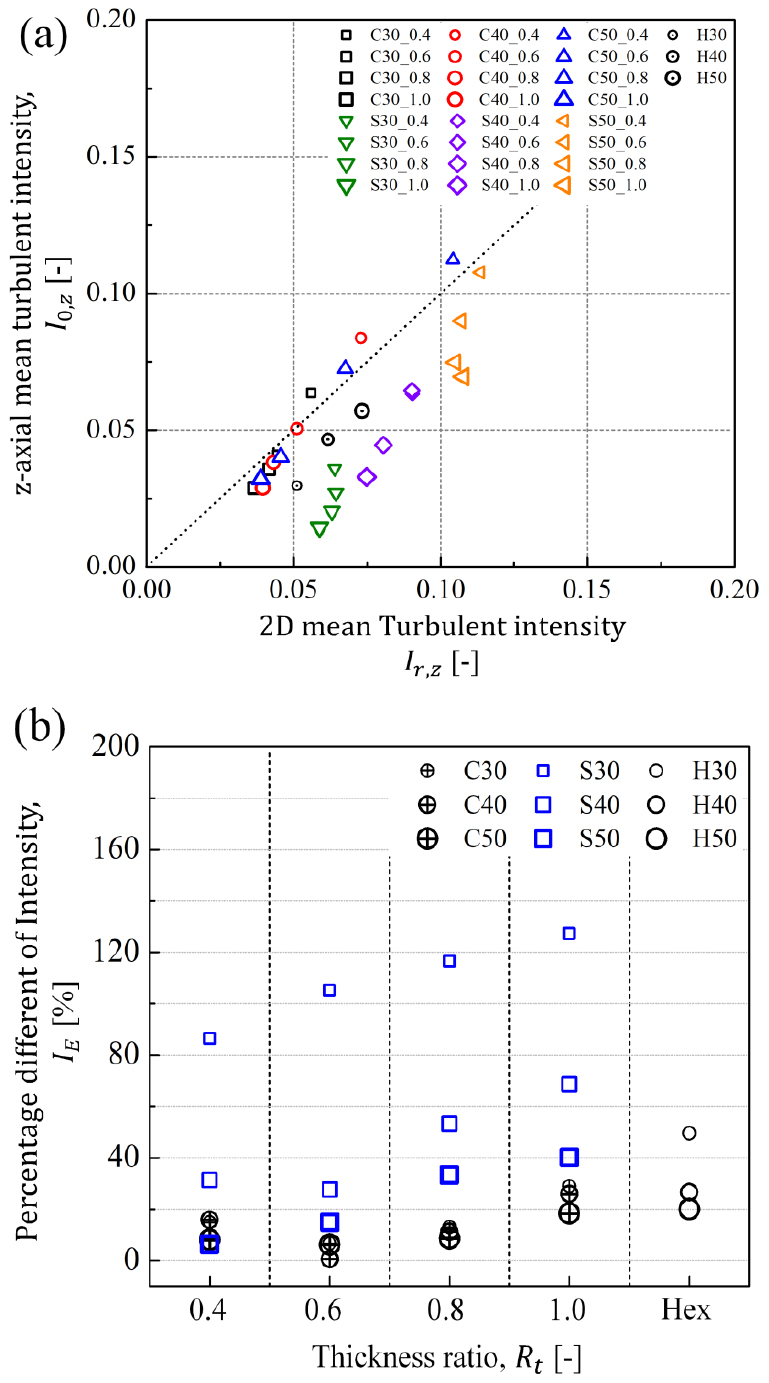
지금까지 (r, z) 평면 난류유동장의 특징을 정성적으로 평가하였고 프랙탈타입 및 주요 형상매개변수에 따라 차이가 있는 것을 확인하였다. 다음으로는 중심축과 평면 데이터의 차이를 정량적으로 확인하여 중심축 데이터의 정확도를 평가하고 균일성을 수치적으로 평가하여 Fig. 16, 17, 18에 나타내었다. Fig. 16, 17, 18의 (a) 그래프는 공통적으로 는 (r, z) 평면 데이터를 평균한 값이며(r = 0 - 12 mm, z = 46 - 76 mm), 는 중심축 데이터(r = 0, z = 46 - 76 mm)를 평균한 값으로 그래프에서 , 값이 동일한 부분은 점선으로 표시하였다(). 그리고 Fig. 16, 17, 18 중 공통적으로 (b) 그래프는 을 나타내는 선과 해당 데이터의 차이 정도를 확인하기 위하여 Fig. 11과 동일하게 다음과 같은 식 (7)으로 정의된 백분율 오차 방법을 사용하여 표현하였다.
여기서 는 비교하고자 하는 값이며, 는 참고하는 값으로 Fig. 16, 17, 18(a)에서의 점선인 = 1에 해당 된다.
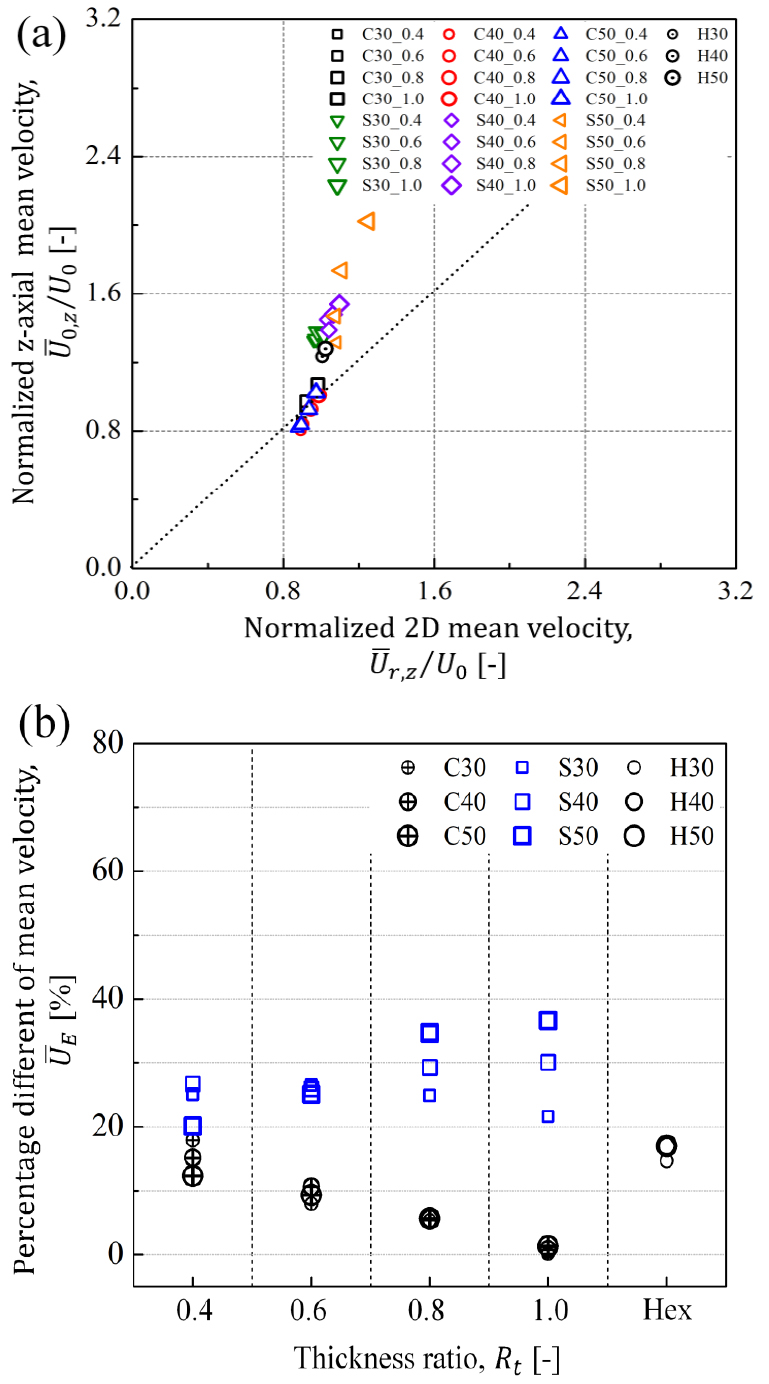
우선, Fig. 16은 무차원화 된 평균속도를 중심축 평균값과 (r, z) 평면 평균값으로 나타내었다. (r, z) 평면의 평균속도를 평균한 값인 는 0.85 - 1.2에 존재하였는데, 난류생성판에서 발생한 난류유동이 비압축성이라 가정하고 비반응장임을 고려하면 질량 보존 법칙을 적용한 연속방정식(continuity equation)으로 인해 을 만족하는 것으로 이해할 수 있다. 그리고 이 근소한 차이는 3차원인 체적 평균값이 아닌 2차원인 (r, z) 평면을 평균하였으므로 Fig. 13에서 관찰되었던 것과 유사하게 평균속도의 비균질성으로로 인해 생긴 결과로 판단된다. Fig. 16(a)에서 나타낸 크로스타입의 결과값은 = 1을 나타내는 점선에 매우 근접하였는데, 이는 중심축 평균속도와 (r, z) 평면의 평균속도를 평균한 값이 상당히 일치한다는 것을 의미한다. 반면에 헥사타입 및 스퀘어타입의 경우 점선 상단에 분포하고 있는 것으로 나타났는데, 이는 중심축에서 측정한 평균속도가 (r, z) 평면을 평균한 값보다 더 높다는 것을 뜻한다. 이와 관련된 통계적 수치는 Fig. 16(b)에서 자세하게 확인할 수 있었으며, 식 (7)을 사용하여 나타낸 크로스타입의 는 보다 에 대한 의존도가 높았으며, 가 낮아질수록 가 선형적으로 증가하여 본 연구에서 사용한 크로스타입의 는 최대 17.9% (C30_0.4)로 비교적 차이가 크지 않았고 헥사타입과 유사했다(H50의 = 17.0%). 반면에 Fig. 16(b) 중 스퀘어타입의 는 크로스와 헥사타입보다 높았으며, S50_1.0의 가 최대 36.6%까지 증가하였다.
Fig. 17은 Fig. 16과 동일한 방법으로 나타낸 속도섭동의 결과값인 를 보여주고 있다. Fig. 17(a) 중 모든 크로스타입의 결과는 Fig. 16(a)의 결과와 유사하게 = 1 점선에 존재하는 것을 볼 수 있으나(최대 28.8% 오차, C30_1.0), 스퀘어타입은 속도섭동이 비교적 높은 대신 점선 밑에 존재하는 것을 알 수 있다. Fig. 17(b)의 통계 데이터에서도 위와 같은 경향을 볼 수 있는데, 흥미로운 점은 스퀘어타입의 S30 조건이 가 월등히 높았다가(최대 = 108.9%, S30_1.0) 이 증가함에 따라 감소하는 것을 볼 수 있는데, 이는 비균질성이 줄어든다는 것을 보여주었다.
Fig. 18은 본 연구의 모든 경우에서 난류강도의 결과값인 이다. 평균속도와 속도섭동의 비균질성으로 인해 난류강도의 경우 더욱 산포되어있는 것을 볼 수 있는데 그럼에도 불구하고 크로스타입의 모든 조건에서는 점선 근처에 존재하였다. 이러한 차이는 Fig. 18(b)에서 명확하게 확인할 수 있으며, 크로스타입과 헥사타입의 최대 오차율은 각각, = 28.9%(C30_1.0), = 49.6%(H30)이며 스퀘어타입의 경우 최대 = 127.3%(S30_1.0)의 큰 오차를 가지고 있는 것으로 확인되었다. 이처럼 모든 타입의 난류생성판들은 = 30%일 때 큰 난류강도 오차율을 가지지만 이 증가함에 따라서 개선되는 것을 확인할 수 있으며, 가 낮아짐에 따라서도 동일하게 적용한다는 것을 보여준다. 이는 저선회 연소기에 실제 사용되는 = 65%이상 조건에서는 더욱 더 균일해질 것으로 판단된다.
정리하자면, 크로스타입의 평균속도, 속도섭동 및 난류강도의 결과값은 모두 = 1인 점선 근처로 분포하여 중심 축 데이터와 (r, z) 평면 데이터의 평균값의 오차율이 작다는 것을 보여주며, 이는 일반타공판 격자보다 난류화가 잘되는 것 뿐 만 아니라 평균속도 및 속도섭동의 균일성 또한 더 우수한 난류생성판으로 평가할 수 있다. 그러나 스퀘어타입의 프랙탈격자는 크로스타입보다 속도섭동이 더 크고 난류화가 잘되는 것으로 보이지만 평균속도 및 속도섭동의 평면 균일성은 다소 떨어진다는 것을 알 수 있으며, 이러한 균일성은 을 증가시키거나 를 감소시키면 일부 해결할 수 있는 가능성을 보여준다.
4. 결 론
후속 연구로 보고하게 될 V-shape 난류화염을 조사하기 앞서 크로스와 스퀘어타입의 프랙탈 패턴을 적용한 원형 난류생성판의 난류증대 효과를 확인하고자 일반타공판인 헥사타입의 난류생성판을 동일한 막힘률로 제작하여 비반응장의 난류특성(성능)을 조사하였고 다음과 같은 결론을 얻었다.
1) 두 프랙탈타입의 주요 형상매개변수인 의 감소, 의 증가에 따라 속도섭동 및 난류강도는 증가하였지만 최대난류강도의 위치는 서로 상반된 경향이 나타났다. 이는 난류생성판에서부터 생성된 난류의 발달영역의 과정이 서로 달라 생긴 현상으로 판단되며, 프랙탈 난류생성판의 주요 형상변수들의 영향을 프랙탈타입 별로 다르게 이해해야 하는 것을 알았다.
2) 동일한 에서 기존 일반형상의 난류생성판인 타공판과 일반매쉬형상과 유사한 크로스타입의 =1.0 조건과 비교를 통해 프랙탈 난류생성판은 타공판에 비해 최대 58%, 일반매쉬와의 비교에서는 최대 99%의 난류강도가 증가되는 것으로 나타나 연소장인 경우에서 난류연소속도 또한 크게 증대될 것으로 예상되었다.
3) 프랙탈 난류생성판에서 생성된 난류유동의 균질성, 속도섭동의 등방성을 확인하기 위하여 노즐출구 이후에서의 (r, z) 평면 유동장에 대한 난류성분들을 측정하였고 기존에 잘 알려진 방법인 중심축에서 측정한 난류성분 인자들과 비교하였다. 평균속도 및 속도섭동의 (r, z) 평면 데이터를 확인한 결과, 프랙탈의 형상 구조에 따라 노즐출구에까지 직접적으로 영향이 있었으며 이 증가할수록 그 경향은 뚜렷하게 관찰되었다.
4) (r, z) 평면데이터의 비균질성 및 중심축 데이터와의 차이를 좀 더 정량적으로 확인하기 위해 중심축과 (r, z) 평면의 난류성분을 백분율 오차를 사용하여 비교하였다. 그 결과, 크로스 프랙탈타입의 난류생성판을 사용할 경우 기존 타공판보다 더 우수한 난류강도를 생성할 수 있었고 (r, z) 평면 유동장도 균일하였다. 하지만 스퀘어 프랙탈타입의 난류생성판은 크로스타입보다 더 강한 난류강도를 생성할 수 있으나 불균일한 평균속도 및 속도섭동을 야기할 수 있음을 보였고 이러한 현상은 이 증가하거나 가 감소함에 따라 개선되는 것을 확인하였다.
기호설명
: Turbulent flame speed [m/s]
: Local displacement speed [m/s]
: Local consumption speed [m/s]
: Bulk velocity [m/s]
: Mean velocity [m/s]
: Radial mean velocity [m/s]
: Percentage different of 2D fluctuation [%]
: Percentage different of 2D intensity [%]
: Nozzle diameter [mm]
: Distance from turbulence generator to the nozzle exit [mm]
: Number of fractal iteration [–]
: Blockage ratio [%]
: Axial mean velocity [m/s]
: Axial velocity fluctuation [m/s]
: Radial velocity fluctuation [m/s]
: Azimuthal velocity fluctuation [m/s]
: Local turbulent intensity [–]
: Reference turbulent intensity [–]
: Percentage different of intensity [%]
: Percentage different of 2D value [%]
: Percentage different of 2D mean velocity [%]
: Area of fractal grid [–]
: Thickness ratio [–]
: Initial bar thickness of the fractal [mm]
: Initial bar length of the fractal [mm]
: i-th thickness of fractal grid [mm]
: i-th length of fractal grid [mm]
: Effective mesh size [mm]
: Wake interaction length scale [mm]
: Fractal perimeter’s length [mm]