Effect of Low Temporal Resolution on the Uncertainty of Resolving Flame Speed of Moving Flames

Dong Hyuk Shin

doi:10.15231/jksc.2020.25.4.037

Preview

Research Article

Journal of The Korean Society Combustion. 31 December 2020. 37-46
https://doi.org/10.15231/jksc.2020.25.4.037

Effect of Low Temporal Resolution on the Uncertainty of Resolving Flame Speed of Moving Flames

저시간 분해능으로 인한 화염 속도 분석의 불확실성

Dong Hyuk Shin¹^†

신 동혁¹^†

¹Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology

¹한국과학기술원 항공우주공학과

^*donghyuk.shin@kaist.ac.kr

ABSTRACT

This paper analyzes the effect of low temporal resolution on the accuracy of determining the local flame speed for experimental measurements and simulations. Flame speed measurement of moving flames requires the evaluation of a temporal derivative of flame front motion. Measurements have limited temporal resolution, which can lead to a bias error in the calculation of flame speed. The error associated with the temporal resolution was derived in the leading order effect on sampling time. In order to demonstrate the error term, we employed numerical examples. Artificial flame solutions are generated by solving the G-equation with prescribed flow fields and fine spatial/temporal resolutions. By varying the sampling time step, we demonstrated the error can lead to negative values of the measured flame speed. Furthermore, when coarse sampling time steps are used, the calculated flame speed also exhibits a spurious curvature dependency. Lastly, the associated error can be estimated by spatial gradients of the flame front for convection dominated flows.

Keywords

Flame speed

Temporal resolution

Negative flame speed

MAIN

1. Introduction
2. Formulation
3. Results and analysis
3.1 Measured flame speed when the first order finite difference for the temporal gradient is employed
3.2 Numerical illustration: flames subject to oscillating flow fields
4. Conclusion

1. Introduction

Flame speed plays a central role in turbulent combustion modelling and is a key physical parameter in understanding combustion systems [1]. In a simplified model, the flame speed is known to depend on the reaction rate and species thermal diffusivity; hence how quickly heat is generated and how fast the heat is transported back to the upstream reactants are the two key parameters [2]. In general laminar conditions, chemical kinetics software is now capable of accurately calculating flame speed [3, 4].

When turbulent fluctuations are present, determination of flame speed becomes challenging. Quite often, turbulent flame is portrayed as wrinkled flame surface perturbed by flow fluctuations. Then, the turbulent flame speed is considered to increase proportionally to the increased surface area due to the wrinkling. However, ambiguity still exists on how to define the reference surface area if the corresponding laminar flame is not flat. Also, if one relates the turbulent flame speed with certain physical processes, various definitions of turbulent flame speeds are possible. If one relates with heat release, the terminology turbulent burning velocity is used and if one relates with the flame front location, then turbulent displacement speed is used [1].

Because of its central role in combustion modelling, an overarching goal in turbulent combustion is to measure flame speed computationally or experimentally. Several direct-numerical simulation (DNS) studies have been conducted to study the intrinsic nature of flame speed with respect to flame structure [5] and flame stretch including strain and curvature [6, 7]. While these studies resolve all time and length scales, the flames under consideration are restricted to simple flame geometries (e.g. a flat flame in a box) at atmospheric temperature and pressures.

As many sophisticated laser diagnostic methods are now available, many researchers have provided measurements of local flame speed in various turbulent flame environments including: bluff body stabilized flames [8, 9], freely propagating flames [10], lifted jet flames [11, 12], and internal combustion engines [13, 14]. Such measurements are providing improved understandings of turbulent combustion in more practical systems and are aiding the development of more predictive numerical modellings.

Within the context of flame speed, both DNS and experimental studies have reported the occurrence of negative flame speed [5, 7, 13]. In such studies the notion of negative flame speed does not pertain to rates of fuel consumption or heat release, but instead pertains to the flame displacement relative to the turbulent flow. Nonetheless, the notion of the negative flame speed is often difficult to fathom for most researchers. DNS studies have revealed three physical mechanisms attributed to negative flame speed:

・strong molecular diffusive effects tangential to flame contours exhibiting high positive curvature [7, 15, 16];

・high compressive or tangential strain [5, 7, 15];

・sensitivities in the prescribed variable to identify the flame front [17].

For experimental measurements, the cause of negative flame speed is less understood. Peterson et al. [14] demonstrated a strong correlation between negative flame speed and flame cusps with positive flame curvature, which is consistent with DNS findings. Most other experimental findings do not have conclusive evidence regarding the cause of negative flame speeds. Determining flame speed from experimental measurements is a challenging feat. Simultaneous velocity and flame position measurements are required and are often three-dimensional (3D) information are further required for measurements in turbulent flow environments [10, 11, 13]. Even when such 3D measurements are possible, measurement uncertainties can bias experimental findings, which could attribute to the occurrence of negative flame speed. The most notable measurement uncertainties affecting calculations include [11, 13]:

・measurement error in velocity and flame position;

・ambiguity defining the flame marker;

・mis-alignment of the velocity and the flame position;

・no or coarse out-of-plane measurement resolution in 3D measurements.

It should also be recognized that experiments and simulations (excluding DNS) are spatially and temporally under-resolved. Especially in turbulent environments, the flame front is not transported uniformly such that spatially resolving flame transport (convection and diffusion) is extremely challenging with a single time-step. These aspects will no doubt affect the calculation in flame speed. While some researchers have discussed the influence of limited spatial resolution with respect to negative flame speed observations [13], the effect on a limited temporal evolution has not been discussed in detail within the literature.

In this paper, we investigated the error associated with temporal resolution in measuring flame speed under laminar conditions. The analysis is based on the G-equation approach, which is an acceptable kinematic model for moving flames in thin reaction zone [18]. We derive the error term associated with the temporal resolution and provide numerical examples for quantitative illustrations.

2. Formulation

The analysis is based on the flame front tracking equation, the so-called G-equation [19], which is formulated as follows:

(1)

\frac{\partial G}{\partial t} + \vec{u} \cdot \nabla G = S_{L} | \nabla G |

where $\vec{u}$ and G are resolved instantaneous values and S_L is the laminar flame speed. The location of the flame front is determined by the iso-contour of G = 0. Alternatively, if the flame position, denoted as $ξ$ , is measured along one coordinate (for example in y), then the G-equation can be re-cast in terms of $ξ$ if a substitution of $G = y - ξ (t, x, z)$ is used:

(2)

\frac{\partial x i}{\partial t} + u \frac{\partial x i}{\partial x} - v + w \frac{\partial x i}{\partial z} = - S_{L} \sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2} + {(\frac{\partial ξ}{\partial z})}^{2}},

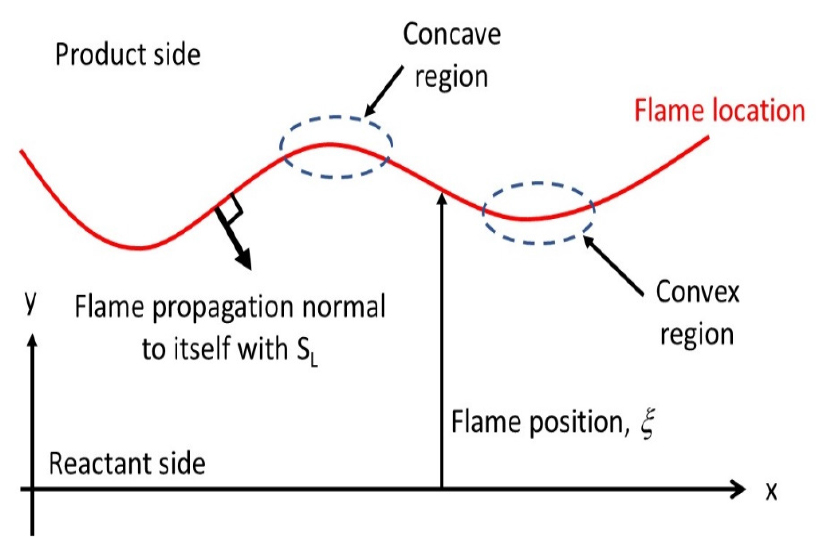
where u, v, and w are the velocity components on the flame position. The negative sign on the right-hand side indicates that the flame overall propagates downward with respect to the y-coordinate. To simplify the analysis, we consider the flow field is two-dimensional as a schematic diagram is illustrated in Fig. 1. As annotated in Fig. 1, we denote that flame position is convex to the reactant where the flame protrudes to the reactant and vice versa for concave region.

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F1.jpg

Fig. 1

A schematic diagram of flame and its coordinates.

If the resolved flow velocities and flame position are available, then one can calculate the laminar flame speed using the G-equation as:

(3)

S_{L} = \frac{- \frac{\partial x i}{\partial t} - u \frac{\partial ξ}{\partial x} + v}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} .

Each parameter on the right-hand side of the above equation will have uncertainties associated with it. Such uncertainties will result in deviation from the actual flame speed. In order to focus on the effect of the temporal resolution, we assume the following conditions to rule out other possibilities.

・Reaction zone is very thin, so that there is no ambiguity defining the flame position.

・At each time, resolved flame position and velocities on the flame position are obtained.

・The spatial resolution is sufficiently fine so that the errors associated with spatial gradients are negligible.

Hence, the only measurement error is associated with temporal derivatives. Then, we define the measured flame speed, S_M, as follows:

(4)

S_{M} = \frac{- {[\frac{\partial ξ}{\partial t}]}_{m e a s u r e d} - u \frac{\partial ξ}{\partial x} + v}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}},

where u, v and $\partial ξ / \partial x$ are the resolved values, while ${[\partial ξ / \partial t]}_{m e a s u r e d}$ is an approximated value from measured flame position. Note that the term “measured” can refer to experimental measurements or simulations, excluding DNS. In this paper, we will derive an error associated with the temporal term and use numerical examples to illustrate the error.

3. Results and analysis

This section is split into two subsections. In the first subsection, the error associated with the temporal gradient term is derived. In the second subsection, numerical examples are presented. Flame positions are generated by solving the G-equation numerically with a constant laminar flame speed. Then, by sampling the solutions coarsely in time, we illustrate that poor temporal sampling can result in negatively measured flame speeds. Note again the measured flame speed refers to S_M, defined in Eq. (4).

3.1 Measured flame speed when the first order finite difference for the temporal gradient is employed

Typically, flame position is measured at discrete time steps. Hence, one way to calculate the temporal gradient is the first order forward finite difference, which is written as follows:

(5)

{[\frac{\partial ξ}{\partial t}]}_{m e a s u r e d} = \frac{ξ (t + ∆ t_{s}) - ξ (t)}{∆ t_{s}},

where $∆ t_{s}$ refers to the sampling time from measurement. The accuracy of the finite difference can be estimated by the following formula, which is obtained by a combination of mean value theorem and Taylor expansion:

(6)

\frac{\partial x i}{\partial t} = \frac{ξ (t + ∆ t_{s}) - ξ (t)}{∆ t_{s}} - \frac{∆ t_{s}}{2} \frac{\partial^{2} ξ (τ)}{\partial t^{2}}, (w h e r e, t < τ < t + ∆ t_{s})

where $\frac{\partial^{2} ξ (τ)}{\partial t^{2}}$ represent the second-order derivative evaluated at $τ$ which is a time between $t$ and $t + ∆ t_{s}$ . Then, if we plug it back to the laminar flame speed equation in Eq. (3), it leads to:

(7)

S_{L} = \underset{S_{M}}{\underset{⏟}{\frac{- \frac{ξ (t + ∆ t_{s}) - ξ (t)}{∆ t_{s}} - ξ \frac{\partial ξ}{\partial x} + v}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}}}} + \underset{e r r o r}{\underset{⏟}{\frac{\frac{∆ t_{s}}{2} \frac{\partial^{2} ξ (τ)}{\partial t^{2}}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}}} .}

In Eq. (7), the first term on the RHS is S_M and, the second term is the associated error. Rearranging the above equation leads to:

(8)

S_{M} = S_{L} - \frac{\frac{\partial^{2} ξ (τ)}{\partial t^{2}}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} \frac{∆ t_{s}}{2} .

Equqation (8) indicates that the measured flame speed, S_M, can become negative if the second term on the RHS is less than -S_L. It is also evident that the error increases proportional to the sampling time ( $∆ t_{s}$ ). The derivation of the error term using the second order central finite difference is shown in Appendix A.

Interestingly, the second order derivative of flame position in time ( $\partial^{2} ξ / \partial t^{2}$ ) is the key parameter that can result in a negative S_M since the rest of terms are all positive. In most cases, the second-order temporal derivative may not be available. However, if the flame is strongly dominated by convection in the x-direction such as bluff-body stabilized flames, then the time derivative can be related to a spatial derivative as

(9)

\frac{\partial^{2} ξ}{\partial t^{2}} \approx u^{2} \frac{\partial^{2} ξ}{\partial x^{2}},

where the derivation is shown in Appendix B. A more sophisticated approximation of $\partial^{2} ξ / \partial t^{2}$ is presented in Eq. (19) on Appendix B, and its resulting analysis is presented in Appendix C.

Using the approximation in Eq. (9), a corrected measured flame speed ( $S_{M, c o r r e c t e d}$ ) can be expressed for the x-convection dominated conditions as:

(10)

S_{M, c o r r e c t e d} \approx S_{L} - \frac{u^{2} \frac{\partial^{2} ξ}{\partial x^{2}}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} \frac{∆ t_{s}}{2} .

Henceforth, this relationship shows that strongly convex regions (i.e., $\partial^{2} ξ / \partial x^{2}$ ≫1) are more likely to result in negatively measured flame speeds due to low temporal resolution if the backward finite difference scheme is employed. Note that the analysis in this section is based on the forward finite difference scheme. If the backward finite difference scheme is employed, Eq. (10) will have a plus sign in the 2^nd term on the right hand side, and the concave region would likely have negatively measured flame speed.

3.2 Numerical illustration: flames subject to oscillating flow fields

We provide numerical examples to highlight the error associated with temporal resolution on the flame speed measurement. Firstly, we generate numerical solutions with very fine spatial and temporal resolutions by the G-equation. Then, we sample the solutions in very coarse time steps to highlight the error due to temporal resolution.

When solving Eq. (2) numerically, the following schemes are used. For spatial derivatives, a weighted essentially non-oscillatory (WENO) scheme is used [20]. This scheme is designed to capture shock profiles, rendering uniformly fifth order accurate in regions where the spatial gradients are smooth and third order accurate in discontinuous regions. A total variation diminishing (TVD) Runge–Kutta scheme up to third order accurate was used for time integration and local Lax-Friedrich (LLF) scheme was used for improved stability [21]. The spatial and temporal grid size were $λ_{0} / 400$ and $1 / (10, 000 f_{0})$ , where $λ_{0}$ and $f_{0}$ are the wave length and the frequency of the imposed flow oscillation. Other parameters and flow conditions are described below.

The following velocity field are chosen as an input:

(11)

u = u_{0} and v = ϵ_{0} \sin (2 π (f_{0} t - \frac{x}{λ_{0}})) .

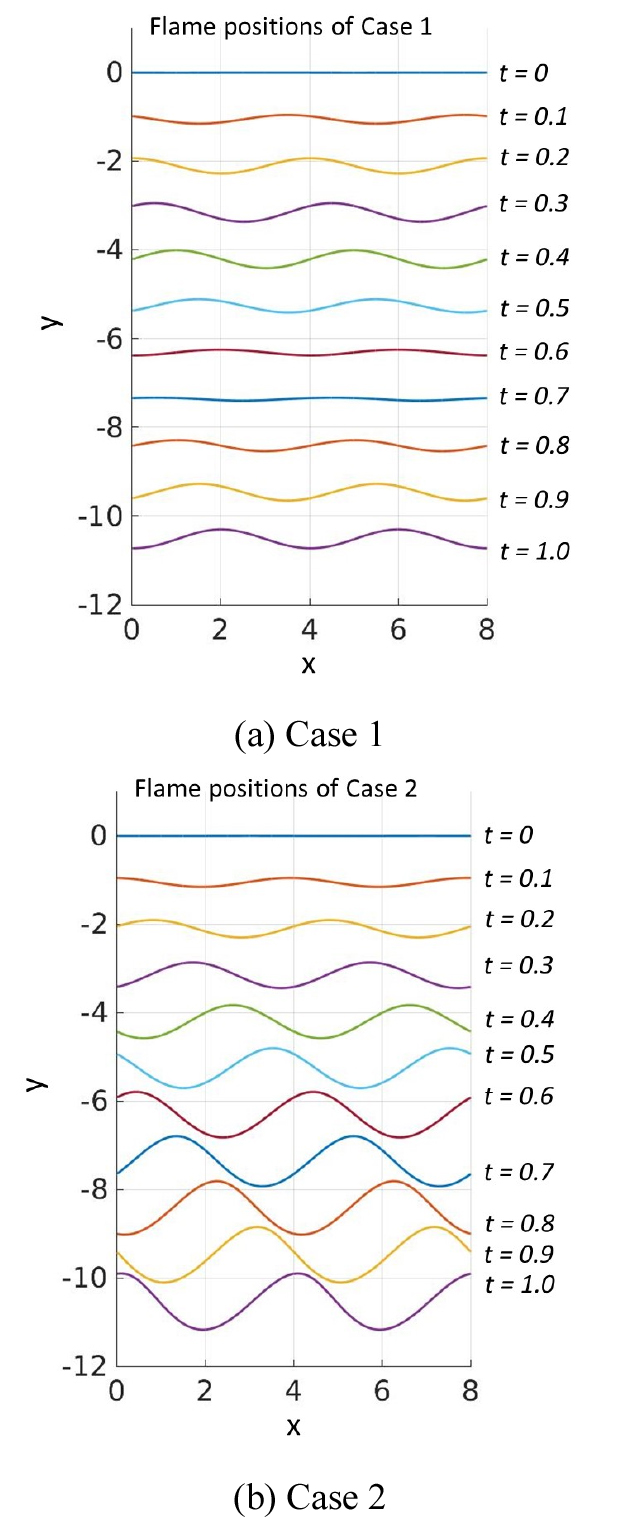
This flow field is chosen such a way that it only depends on x and t to simplify the analysis. Note that all variables are dimensionless for simplification, and the laminar flame speed is set to be constant for simpler analysis. Two cases are simulated whose parameters are listed in Table 1. Case 1 represents the condition where the associated velocities are of comparable magnitudes of each other. Case 2 represents an x-convection dominated case, i.e. u ≫ S_L and u ≫ v.

Table 1.

List of parameters for the simulations

	Case 1	Case 2
$u_{0}$	2	10
$S_{L}$	0.5	0.5
$ε_{0}$	1	1
$f_{0}$	2	2
$λ_{0}$	4	4

For both cases, the initial flame positions are set to be flat, and the periodic boundary condition is imposed on the boundaries. Fig. 2 shows the calculated instantaneous flame position of Case 1 and Case 2.

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F2.jpg

Fig. 2

Simulated flame positions from t = 0 to 1.

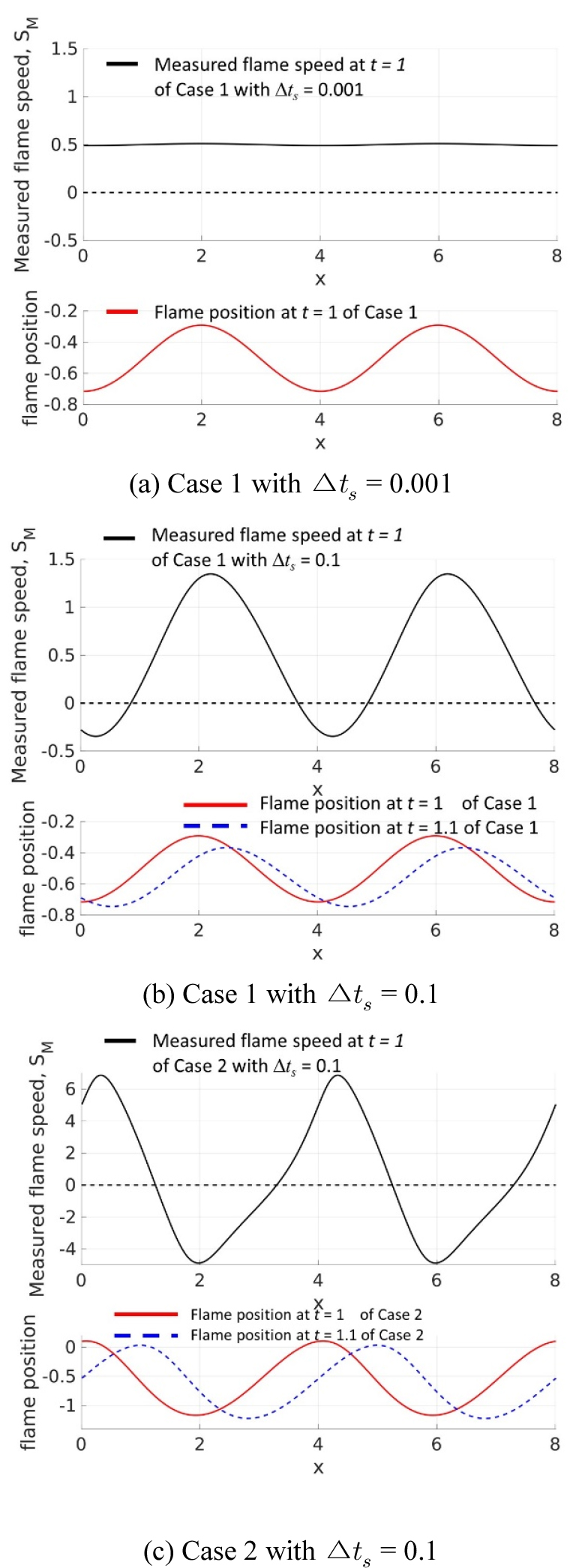
Note that as the frequency is 2, the period of the oscillation is 0.5. The next step is to calculate the measured flame speed (S_M) from the simulated flame positions and the given velocities. Fig. 3(a) and (b) show the measured flame speed from Case 1 utilizing Eq. (7). The only difference between the two figures is the employed $∆ t_{s}$ . In Fig. 3(a), a fine time step of $∆ t_{s}$ = 0.001 is used, while a coarse time step of $∆ t_{s}$ = 0.1 is used for Fig. 3(b). As a reference, the flame position at 0.1 later is shown in a dashed line in Fig. 3(b). Fig. 3(c) shows the measured flame speed from Case 2 with $∆ t_{s}$ = 0.1.

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F3.jpg

Fig. 3

The measured flame speed from the first order finite difference (tops) and instantaneous flame positions (bottoms) at t = 1.

When the fine time step ( $∆ t_{s}$ = 0.001) is used, the calculation reproduced the imposed, constant flame speed at all x-locations. On the other hand, when the coarse time step ( $∆ t_{s}$ = 0.1) is used, the calculation shows an oscillatory measured flame speed over x, and even reaching negative values. This clearly indicates the associated errors due to the coarse time step that leads to negatively measured flame speeds even though the imposed flame speed is constant. Case 2, with the coarse time step of $∆ t_{s}$ = 0.1, shows the same trends of an oscillatory flame speed over x and observed negative values of flame speed as shown in Fig. 3(c).

Next, Fig. 4(a) shows the correlations between the local curvature and the measured flame speed at t = 1 of both cases when the low sample times ( $∆ t_{s}$ = 0.05 or 0.1) are employed. The local curvature (k) is defined as $(\partial^{2} ξ / \partial x^{2}) / {(1 + {[\partial ξ / \partial x]}^{2})}^{3 / 2}$ . This indicates that an artificial curvature dependency may arise if the time resolution is low even though the imposed laminar flame speed is independent of the curvature. The artificial curvature dependency becomes stronger if the sampling time is larger – the overall slopes are steeper at $∆ t_{s}$ = 0.1 comparaed to $∆ t_{s}$ = 0.05 for both cases.

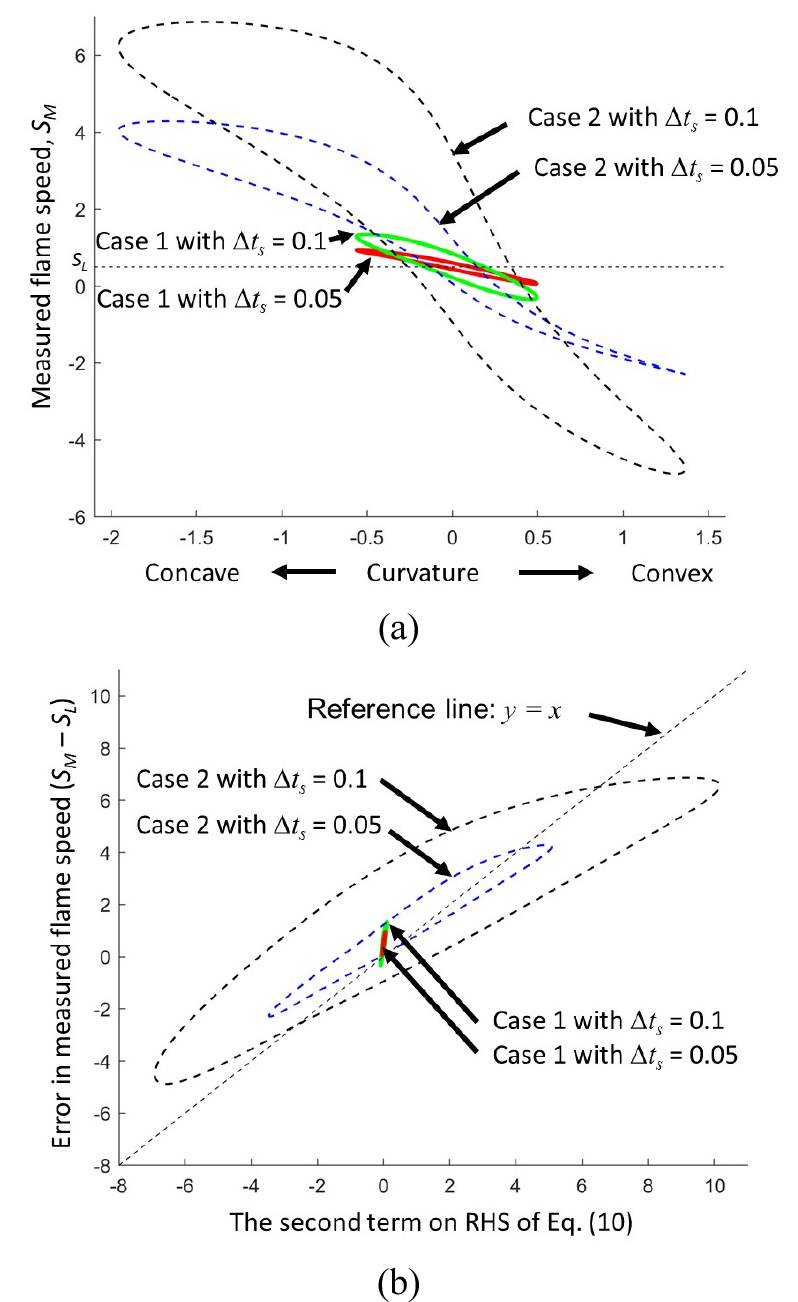
https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F4.jpg

Fig. 4

(a) The correlation between the measured flame speed and the local curvature at t=1 when $∆ t_{s}$ =0.05 and $∆ t_{s}$ =0.1 are employed and (b) the correlation between the error in the measured flame speed and the error term in Eq. (10) at t=1. (Note that the forward finite difference scheme is used for all conditions.)

The results on Fig. 4(a) indicate that the negatively measured flame speed occurs in the convex region, which is in line with the observations in the previous studies [7, 11, 14,15,16]. However, note that the analysis in the paper is based on the forward finite difference scheme. If the backward finite difference scheme is used, then the calculated flame speed will show the opposite trend: the negatively measured flame speed occurs in the concave region. It is difficult to further compare with the previous studies as other condition might play roles such as actual curvature dependency of the fuel, uncertainties other than time resolution, or different numerical algorithms to calculate the flame speed. For example, Peterson et al. [14] employed the 2^nd order central difference scheme where the errors due to low temporal resolution will be smaller by the order of magnitude than the illustrated here - see Appendix A.

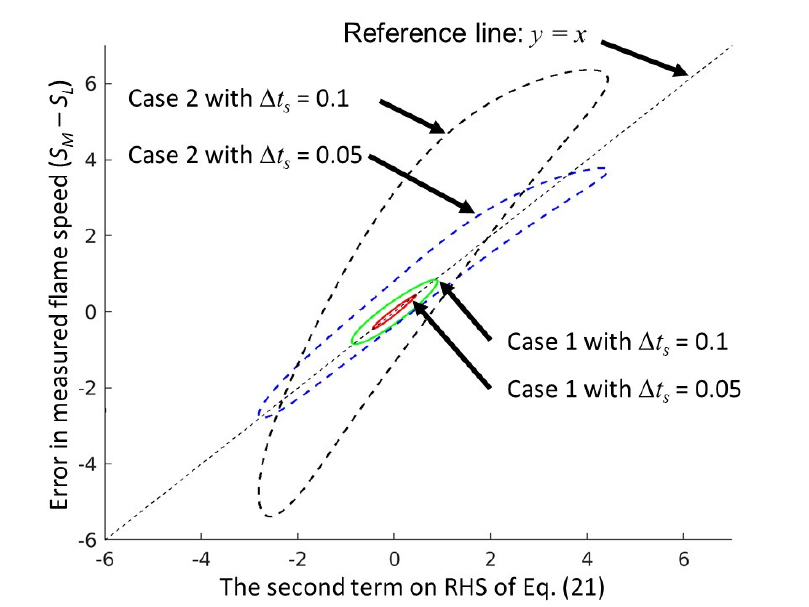
Fig. 4(b) shows the correlation between the measured flame speed and the error term in Eq. (10). As a reference, a straight line of y = x, is overlaid. The solid lines (Case 1) have quite different slopes than the reference line while the dashed lines (Case 2) are more aligned to the reference line. This indicates that the second term in Eq. (10) is a good indicator for error estimation for convection dominated cases. Note that a similar analysis is conducted with a more sophisticated approximation and its result is presented in Appendix C.

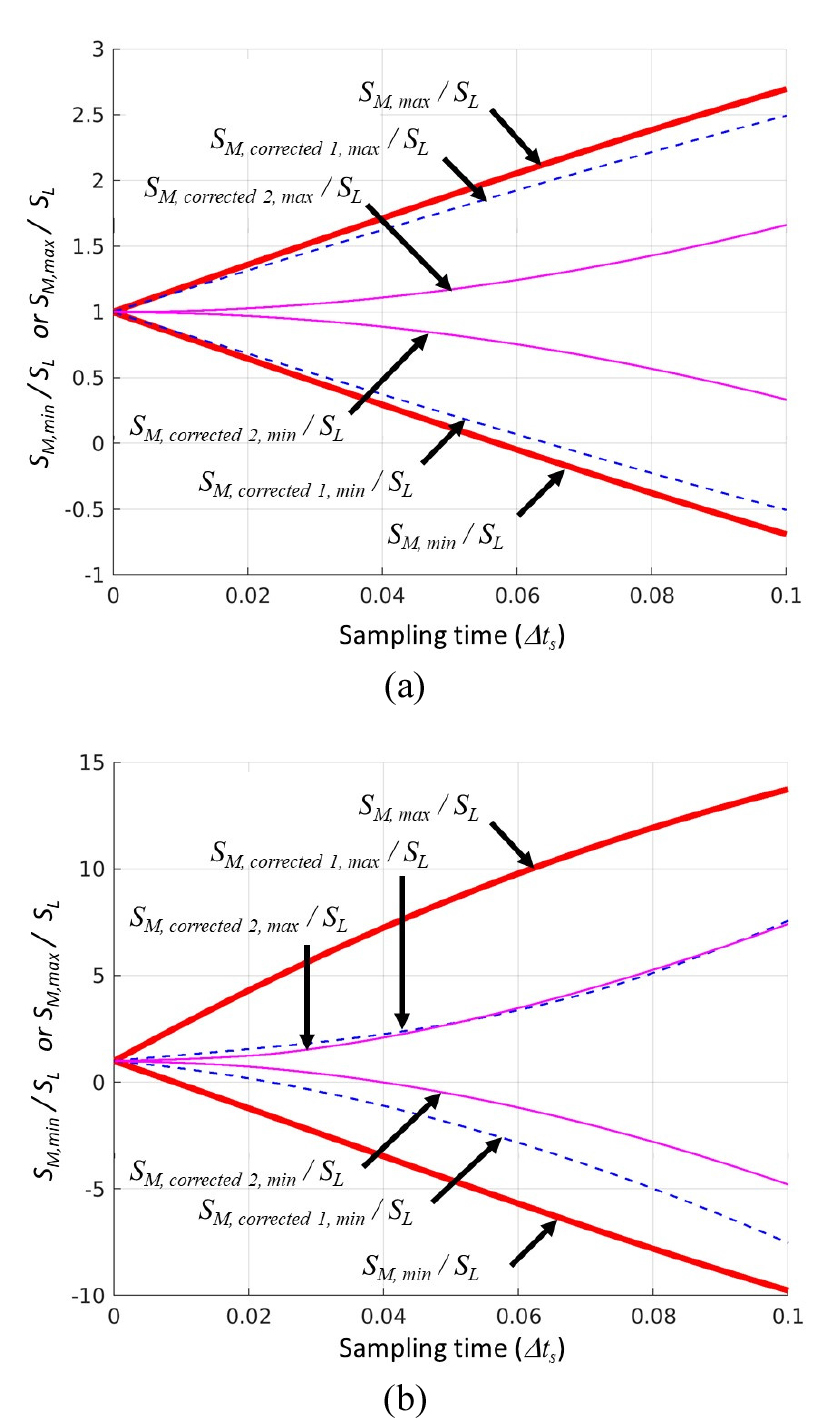
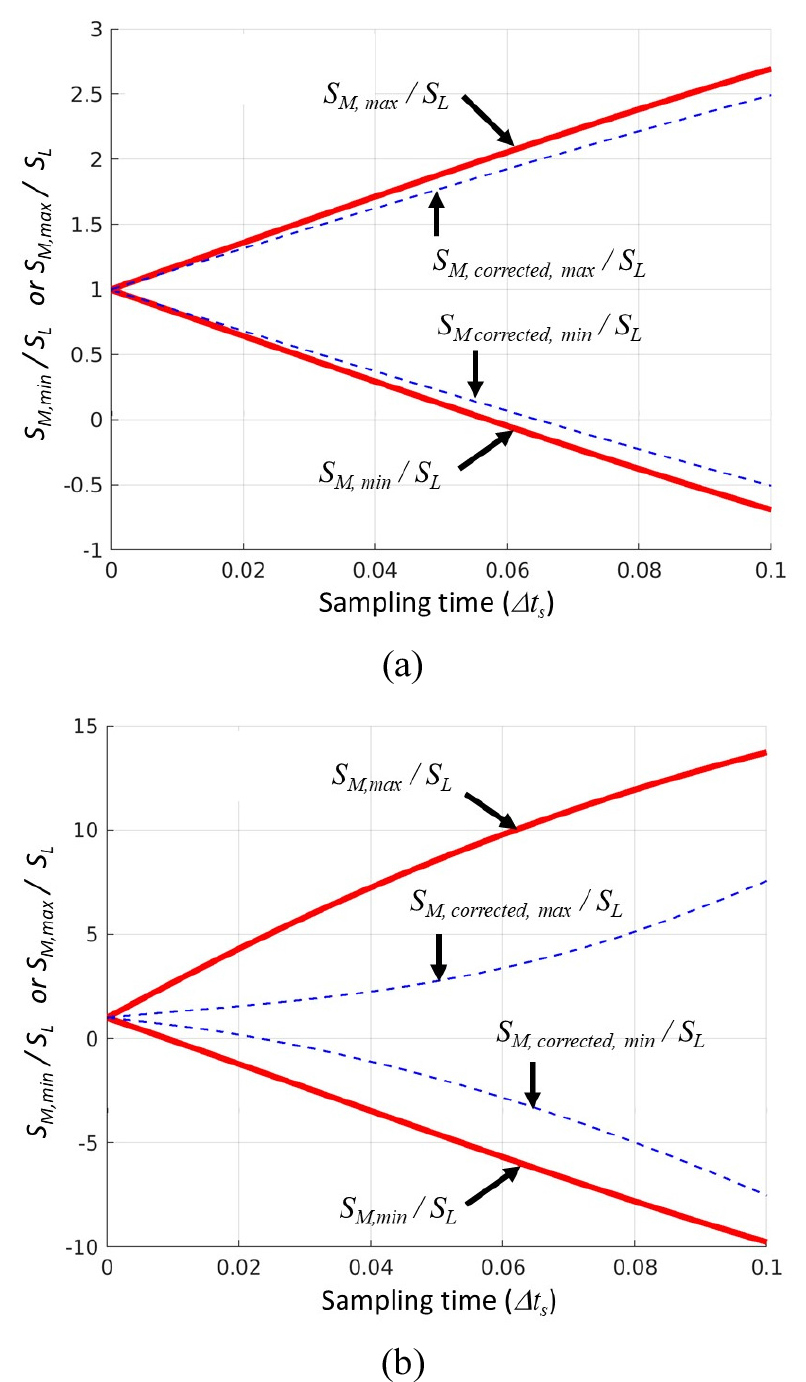
Fig. 5 shows the dependency of the maximum and minimum of measured flame speed (S_M) over the sampling time at t=1. As the actual laminar flame speed is constant, any value away from the unity is considered as an error. Hence, the maximum and minimum of the measured flame speed at t=1 represents the extent of the error due to the temporal resolution. Overall, as the sampling time increases, the error grows linearly for all conditions, which is consistent with the derivation in Eq. (8).

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F5.jpg

Fig. 5

Dependency of the maximum and minimum of measured flame speed over the sampling time. S_M is referred in Eq. (7), and S_M, _corrected is referred in Eq. (10). Other conditions are (a) case 1 and (b) case 2.

Two different measured flame speeds are drawn in the figure: S_M in Eq. (7) and S_{M, correct} in Eq. (10). For case 1 (shown in Fig. 5(a)), the correction barely reduced the error. On the other hands, for case 2 (shown in Fig. 5(b), the correction greatly reduces the error by a factor of two. Note that the correction in Eq. (10) is derived based on the convection dominated assumption. Hence, the correction is applied well to case 2 as it is a convection dominated case.

Note that a more sophisticated correction and its corresponding results are presented in Appendix C. The sophisticated correction greatly reduces the error for both case 1 and case 2. However the sophisticated correction requires additional information such as velocity gradients and the characteristic speed of disturbances. Hence, its practical application might be limited.

4. Conclusion

The coarse temporal resolution in flame derivatives are investigated as a source of error for flame speed measurement. The Taylor expansion approach shows that the obtained flame speed can be negative as an artifact of coarse time resolution. An exact formula and an approximate formula were derived. When the first order finite difference scheme is used, the analysis indicates that the error is associated with the second derivative of time. For convection dominated flames, the second-order derivative of time can be estimated by the second-order derivative in space. As curvature includes the second-order spatial derivative in the definition, and this indicates that the associated error is related to the curvature.

This manifestation was illustrated by numerical examples where a constant flame speed is imposed. The numerical solutions were generated by the G-equation with very fine spatial and temporal resolutions. Then, the flame speed is measured from the simulated flame positions by employing different sampling time steps. When the fine sampling time step is used, the measured flame speed reproduced the imposed constant flame speed. However, when the coarse time step is applied, the measured flame speed became oscillatory, even reaching negative values. The associated error is linearly proportional to the sampling time step. Furthermore, the measured flame speed by the coarse time step shows an artificial dependency with the flame curvature. The trend between the measured flame speed and the curvature depends on the employed numerical scheme (backward or forward finite difference). For convection dominated cases, the deviation from the actual flame speed can be estimated by the second-order derivative in space.

Appendix

A. Associated error when emploting the second order central finite difference.

Higher order finite difference scheme provides smaller errors. Hence, the second order central difference scheme is frequently used, which is written as follows:

(12)

{[\frac{\partial ξ}{\partial t}]}_{m e a s u r e d, 2} = \frac{ξ (t + ∆ t_{s}) - ξ (t - ∆ t_{s})}{2 ∆ t_{s}} .

Applying the similar analysis, the measured flame speed, S_M,2, becomes:

(13)

S_{M, 2} = S_{L} - \frac{\frac{1}{6} \frac{\partial^{3} ξ (τ)}{\partial t^{3}}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} ∆ t_{s}^{2}, (where, t - ∆ t_{2} \leq τ \leq t + ∆ t_{s})

Again, for strongly convection dominated flames, the temporal gradient can be related as follows:

(14)

\frac{\partial^{3} ξ}{\partial t^{3}} \approx - u^{3} \frac{\partial^{3} ξ}{\partial x^{3}} .

Hence, the measured flame speed for convection dominated cases is expressed as:

(15)

S_{M, 2} = S_{L} + \frac{\frac{u^{3}}{6} \frac{\partial^{3} ξ}{\partial t^{3}}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} ∆ t_{s}^{2} .

B. Relation of the second derivative for convection dominated cases

Assuming $(\partial ξ / \partial x)^{2}$ ≪1, Eq. (2) is rewritten in the two dimension as follows:

(16)

\frac{\partial ξ}{\partial t} + u \frac{\partial ξ}{\partial x} - v \approx - S_{L .}

Differentiate the equation with respect to time which leads to:

(17)

\frac{\partial^{2} ξ}{\partial t^{2}} + u \frac{\partial}{\partial x} (\frac{\partial ξ}{\partial t}) + \frac{\partial u}{\partial t} \frac{\partial ξ}{\partial x} - \frac{\partial v}{\partial t} \approx 0 .

Substitute $\partial ξ / \partial t$ with Eq. (16) and assume $\partial u / \partial t$ and $\partial u / \partial x$ are small, then the above equation is transformed into:

(18)

\frac{\partial^{2} ξ}{\partial t^{2}} - u^{2} \frac{\partial^{2} ξ}{\partial x^{2}} + u \frac{\partial v}{\partial x} - \frac{\partial v}{\partial t} \approx 0 .

If the y-velocity has a certain characteristic speed, c, then $\partial v / \partial t$ can be replaced by $- c (\partial v / \partial x)$ . For example, if v satisfies the equation in Eq. (11), then $c = λ_{0} f_{0}$ . With this replacement, Eq. (18) is rearranged as:

(19)

\frac{\partial^{2} ξ}{\partial t^{2}} \approx u^{2} \frac{\partial^{2} ξ}{\partial x^{2}} - (u + c) \frac{\partial v}{\partial x} .

Finally, if $\partial v / \partial x$ is further assumed to be negligible, $\partial ξ / \partial t$ can be approximated as:

(20)

\frac{\partial^{2} ξ}{\partial t^{2}} \approx u^{2} \frac{\partial^{2} ξ}{\partial x^{2}} .

C. S_{M,corrected 2}using a more sophisticated approximation

In this section, Eq. (10), Fig. 4(b) and Fig. 5 are reproduced using a more sophisticated approximation. If the approximation of Eq. (19) is used for correction, a corrected measured flame speed is written as:

(21)

S_{M, c o r r e c t e d 2} \approx S_{L} - \frac{u^{2} \frac{\partial^{2} ξ}{\partial x^{2}} - (u + c) \frac{\partial ㅍ}{\partial x}}{\sqrt{1 + {(\frac{\partial ξ}{\partial x})}^{2}}} \frac{∆ t_{s}}{2} .

Fig. 6 shows the correlation between the error in the measured flame speed and the second term in Eq. (21) - a reproduction of Fig. 4(b) with the more sophisticated correction. The correlations shows that the error is very well aligned with the second term in Eq. (21) for case 1 which is not convection-dominated. For case 2 with $∆ t_{s} = 0.1$ , the degree of mis-alignment is similar to the one presented in Fig. 4(b).

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F6.jpg

Fig. 6

Reproduction of Fig. 4(b) with a more sophisticated approximation: the correlation between the error in the measured flame speed and the error term in Eq. (21) at t=1. (Note that the forward finite difference scheme is used for all conditions.)

Fig. 7 shows the dependency of the maximum and minimum of measured flame speeds over the sampling time. S_M is referred in Eq. (7), S_{M,corrected 1} is referred in Eq. (10), and S_{M,corrected 2} is the one referred in Eq. (21). For all conditions, S_{M,corrected, 2}greatly reduced the error. However, note that S_{M,corrected, 2}requires additional information of a velocity gradient and the characteristic speed of disturbance. Hence, its application can be limited.

https://static.apub.kr/journalsite/sites/kosco/2020-025-04/N0590250405/images/ksssf_25_04_05_F7.jpg

Fig. 7

Reproduction of Fig. 5 with a more sophisticated approximation. Dependency of the maximum and minimum of measured flame speed over the sampling time.

Acknowledgements

이 논문은 2020년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임 (20206710100060, 분산발전 가스터빈용 수소전소 저 NO_X 연소기 개발).

References

J.F. Driscoll, Turbulent premixed combustion: Flamelet structure and its effect on turbulent burning velocities, Prog. Energy Combust. Sci., 34 (2008) 91-134. 10.1016/j.pecs.2007.04.002

I.B. Zeldovich, G.I. Barenblatt, V.B. Librovich, G.M. Makhviladze, Mathematical theory of combustion and explosions, Plenum Press, New York, 1985. 10.1007/978-1-4613-2349-5

D.G. Goodwin, H.K. Moffat, R.L. Speth, Cantera: An object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes, Caltech Pasadena CA, 2009.

R.J. Kee, F.M. Rupley, J.A. Miller, Chemkin-Ⅱ: A Fortran chemical kinetics package for the analysis of gas-phase chemical kinetics, Sandia National Labs., Livermore, CA(USA), 1989. 10.2172/5681118PMC2448549

J.H. Chen, H.G. Im, Correlation of flame speed with stretch in turbulent premixed methane/air flames, Symp. Int. Combust., 27 (1998) 819-826. 10.1016/S0082-0784(98)80477-3

J.H. Chen, H.G. Im, Stretch effects on the burning velocity of turbulent premixed hydrogen/air flames, Proc. Combust. Inst., 28 (2000) 211-218. 10.1016/S0082-0784(00)80213-1

E.R. Hawkes, J.H. Chen, Comparison of direct numerical simulation of lean premixed methane-air flames with strained laminar flame calculations, Combust. Flame, 144 (2006) 112-125. 10.1016/j.combustflame.2005.07.002

G. Hartung, J. Hult, R. Balachandran, M. R. Mackley, C. F. Kaminski, Flame front tracking in turbulent lean premixed flames using stereo PIV and time- sequenced planar LIF of OH, Appl. Phys. B, 96 (2009) 843-862. 10.1007/s00340-009-3647-0

L.J. Humphrey, B. Emerson, T.C. Lieuwen, Premixed turbulent flame speed in an oscillating disturbance field, J. Fluid Mech., 835 (2018) 102-130. 10.1017/jfm.2017.728

P.J. Trunk, I. Boxx, C. Heeger, W. Meier, B. Bohm, A. Dreizler, Premixed flame propagation in turbulent flow by means of stereoscopic PIV and dual-plane OH-PLIF at sustained kHz repetition rates, Proc. Combust. Inst., 34 (2013) 3565-3572. 10.1016/j.proci.2012.06.025

J. Kerl, C. Lawn, F. Beyrau, Three-dimensional flame displacement speed and flame front curvature measurements using quad-plane PIV, Combust. Flame, 160 (2013) 2757-2769. 10.1016/j.combustflame.2013.07.002

J.R. Osborne, S.A. Ramji, C.D. Carter, A.M. Steinberg, Relationship between local reaction rate and flame structure in turbulent premixed flames from simultaneous 10 kHz TPIV, OH PLIF, and CH2O PLIF, Proc. Combust. Inst., 36 (2017) 1835-1841. 10.1016/j.proci.2016.07.124

B. Peterson, E. Baum, B. Bohm, A. Dreizler, Early flame propagation in a spark-ignition engine measured with quasi 4D-diagnostics, Proc. Combust. Inst., 35 (2015) 3829-3837. 10.1016/j.proci.2014.05.131

B. Peterson, E. Baum, A. Dreizler, B. Bohm, An experimental study of the detailed flame transport in a SI engine using simultaneous dual-plane OH-LIF and stereoscopic PIV, Combust. Flame, 202 (2019) 16-32. 10.1016/j.combustflame.2018.12.024

N. Chakraborty, Comparison of displacement speed statistics of turbulent premixed flames in the regimes representing combustion in corrugated flamelets and thin reaction zones, Phys. Fluids, 19 (2007) 105109. 10.1063/1.2784947

I.R. Gran, T. Echekki, J.H. Chen, Negative flame speed in an unsteady 2-D premixed flame: A computational study, Symp. Int. Combust., 26 (1996) 323-329. 10.1016/S0082-0784(96)80232-3

Y.-C. Chen, R.W. Bilger, Experimental investigation of three-dimensional flame-front structure in premixed turbulent combustion-I: hydrocarbon/air bunsen flames, Combust. Flame, 131 (2002) 400-435. 10.1016/S0010-2180(02)00418-2

N. Peters, Turbulent Combustion, Cambridge University Press, Cambridge, 2000. 10.1017/CBO9780511612701

F.A. Williams, Combustion Theory, CRC Press, Florida, 1985.

G. Jiang, D. Peng, Weighted ENO Schemes for Hamilton-Jacobi Equations, SIAM J. Sci. Comput., 21 (2000) 2126-2143. 10.1137/S106482759732455X

S. Gottlieb, C.-W. Shu, Total variation diminishing Runge-Kutta schemes, Math. Comput. Am. Math. Soc., 67 (1998) 73-85. 10.1090/S0025-5718-98-00913-2

Journal of The Korean Society Combustion ISSN:1226-0959(Print) 2466-2089(Online) 한국연소학회지

Preview

Effect of Low Temporal Resolution on the Uncertainty of Resolving Flame Speed of Moving Flames

ABSTRACT

MAIN

(1)

(2)

Fig. 1

A schematic diagram of flame and its coordinates.

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Table 1.

List of parameters for the simulations

Fig. 2

Simulated flame positions from t = 0 to 1.

Fig. 3

The measured flame speed from the first order finite difference (tops) and instantaneous flame positions (bottoms) at t = 1.

Fig. 4

Fig. 5

Dependency of the maximum and minimum of measured flame speed over the sampling time. SM is referred in Eq. (7), and SM, corrected is referred in Eq. (10). Other conditions are (a) case 1 and (b) case 2.

(12)

(13)

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

Fig. 6

Reproduction of Fig. 4(b) with a more sophisticated approximation: the correlation between the error in the measured flame speed and the error term in Eq. (21) at t=1. (Note that the forward finite difference scheme is used for all conditions.)

Fig. 7

Reproduction of Fig. 5 with a more sophisticated approximation. Dependency of the maximum and minimum of measured flame speed over the sampling time.

Acknowledgements

References

Dependency of the maximum and minimum of measured flame speed over the sampling time. S_M is referred in Eq. (7), and S_M, _corrected is referred in Eq. (10). Other conditions are (a) case 1 and (b) case 2.