Diagnosis of Combustion Instability Using Waveform Pattern of Dynamic Pressure Signal

Seungkyu Choi; Daesik Kim

doi:10.15231/jksc.2024.29.1.033

Preview

Research Article

Journal of The Korean Society Combustion. 31 March 2024. 33-38
https://doi.org/10.15231/jksc.2024.29.1.033

Diagnosis of Combustion Instability Using Waveform Pattern of Dynamic Pressure Signal

동압 신호의 파형-패턴 분석을 통한 연소 진동 진단

Seungkyu Choi¹

Daesik Kim¹^†

최 승규¹

김 대식¹^†

¹Department of Mechanical Engineering, Gangneung-Wonju National University

¹강릉원주대학교 기계공학과

^{*Corresponding Author}

ABSTRACT

This study introduces a new concept that can evaluate the combustion status from the waveform patterns of the dynamic pressure signal, and an initial investigation result on the possibility of combustion instability monitoring, by classifying the waveform of time-series discrete dynamic pressure data, measured in a gas turbine combustor. Based on variations in amplitude among four continuously adjacent data points of dynamic pressure, there are 24 waveform patterns that can be classified. These patterns can be further streamlined to derive three representative diagnostic factors. The representative factors tended to converge to the specific values when combustion instability occurred. Furthermore, distinct characteristic value distributions were observed in stable and transitional states, respectively. These results implied that the waveform pattern, newly defined in this study, can be effectively used as a combustion instability diagnostic tool.

Keywords

Combustion instability

Diagnosis

Waveform pattern

Classification

MAIN

1. 서 론
2. 동압 신호의 계측 및 처리
2.1 실험 데이터 획득 조건
2.2 동압 신호 데이터 처리
3. 진단 성능 분석
4. 결론 및 향후 계획

기 호 설 명

$i$ : arbitrary sequence of data

$k$ : data size of subset

$t$ : time

$p'$ : dynamic pressure

$\bar{p}$ : static pressure

P : permutation

1. 서 론

연소불안정(combustion instability)은 연소 진동 또는 연소 직접 소음(direct noise)이라고도 불리며, 연소 시스템에서 음향 섭동과 화염면 섭동 사이의 상호 작용으로부터 발생하는 현상[1]이다. 이 현상은 발전용 가스터빈의 운전 시 질소산화물과 더불어 실시간으로 모니터링되는 요소이며, 특별히 관리해야 하는 주요 운전 인자 중 하나로 여겨지고 있다[2]. 대부분의 발전용 가스터빈에서는 연소 진동 현상을 모니터링하기 위해 연소실 내부의 특정 위치에 설치된 동압 센서에서 계측되는 신호를 활용하고 있으며, 이를 실시간으로 진단 또는 후처리를 진행하여 연소 안정성[3]을 진단하고 있다. 연소 동압 신호는 고속의 샘플링 주기를 갖는 동압 센서를 통해 이산 시간(discrete time) 형태의 데이터로 기록되며, 빠른 샘플링 속도를 갖기 때문에 민감하게 연소 상태를 판단할 수 있다는 장점을 가지고 있다. 그리고 일반적으로 이 데이터는 고속푸리에변환(fast Fourier transform)을 통해 크기와 주파수 데이터로 변환되어 모니터링되고 있으며, 현재까지 연소 불안정 관점에서 연소 상태를 판단하기 위한 가장 직관적인 수단[4]으로 활용되고 있다. 그러나 계측 신호가 과도 응답 상태(transient response state)를 보일 때 주파수 분해 능력이 저하되는 특징을 보이는 단점[5]이 있는데, 빠른 시간에 급변하는 연소의 특성상 이러한 진단 성능의 저하는 연소 상태 진단에 있어 한계를 갖게 하며, 따라서 안정적인 연소 상태를 유지하기 위해서는 이를 극복할 수 있는 새로운 연소 상태 진단 기법의 도입이 요구된다[6].

최근 많은 연구그룹에서 연소 상태를 실시간으로 파악 및 진단할 수 있는 새로운 진단 기법에 대한 개발 및 연구가 이루어지고 있다. Song et al.[7]은 로켓 엔진과 연구실 규모의 예혼합 연소기 등에서 계측된 이산 동압 신호를 일정 비율로 샘플링하고 이에 대한 첨도(kurtosis) 분석을 통해, 첨도 값이 1.5에 가까울수록 연소 진동 발생과 가까워진다는 연구 결과를 발표하였다. Joo et al.[8]은 신호의 파형이 영점을 통과하는 순간을 정량화한 ZCR(Zero Crossing Rate) 기법을 이산 동압 신호에 적용 및 정량화하였고, 연소 진동이 발생할 때 이 값이 일정해지는 특징을 포착했으며, 이를 활용하면 연소 진동을 진단 해낼 수 있음을 보였다. Choi et al.[9]은 동압 신호의 확률분포를 정량화한 EoE(Entropy of Energy) 방법을 제시하였으며, 연소 진동의 발생 시 이 값이 급격한 기울기를 갖는 특징에 착안해 연소 진동의 진단이 가능함을 보였다. 앞서 소개한 진단 기법들은 연소불안정이 발생하여 한계진폭(limit cycle amplitude)에 이른 상태를 모두 성공적으로 진단해 내는 것으로 보고되었다. 그러나, 일부 진단 모델의 경우 연소 상태가 안정 상태에서의 노이즈(noise) 또는 과도기적(transient) 거동을 보이는 동압 신호 구간에서는 오류 또는 진단 성능 개선의 필요성이 나타나기도 하였다.

본 연구에서는 기존의 진단 모델의 한계를 개선하고자 이산 동압 신호 데이터를 대상으로 새로운 연소 진동 진단 기법의 개발을 위한 기초연구 단계로써 동압 신호의 파형(waveform)이 보이는 패턴(pattern)에 대한 분석연구를 진행하였다. 해당 분석 방법은 연속된 이산 신호 데이터의 진폭(magnitude) 값의 분포가 특정 패턴에 수렴하는 정도를 정량화한 방법이다. 동압 신호는 연소 진동의 발생 시 그 파형이 정현파에 가까워지는 특징이 있는데, 본 연구에서는 이러한 연소 상태 거동에 착안하여 분류되는 패턴 값의 추세를 분석하였다. 이로부터 새롭게 제안되는 파형 패턴(waveform pattern) 진단 모델을 통하여 안정-과도기-불안정 상태의 동압 구간에서의 데이터 특성을 구분하고, 향후 연소불안정 진단에 있어 활용 방안을 제시하고자 한다.

2. 동압 신호의 계측 및 처리

2.1 실험 데이터 획득 조건

동압 신호 데이터는 한국기계연구원(Korea Institute of Machinery & Materials)에서 300 MWe급 대형 발전용 가스터빈을 대상으로 50% 수소혼소 특성 연구를 진행할 목적으로 제작한 실스케일의 단일 캔 연소시험 설비로부터 얻어진 데이터이다[10]. Fig. 1에 해당 연소기에 대한 개략도 및 동압 센서(106B, PCB)의 설치 위치를 나타내었으며, Table 1에는 실험 운전 조건을 요약하였다. 본 연구에 사용된 동압 신호는 Fig. 1에서의 노즐 조립체(nozzle assembly) 중 DP6에 위치한 동압 센서로부터 약 10 초간 계측되었고, 이때 샘플링 주기는 10 kHz이다. 연소시험은 Table 1과 같이 정압 150 kPa, 흡기온도 445°C, 공기유량 1.334 kg/s 조건에서 진행되었으며, 노즐 조립체에서 각 노즐의 당량비를 0.451~0.539, 그리고 연료 중 수소의 부피비를 0~55%로 가변시키며 수행되었다. 해당 실험에 대한 기초 연구 결과는 참고문헌[10]에서 확인할 수 있다. 이외에 동압 신호에 대한 연소불안정 발생의 판단 기준은 연소실 평균 압력 대비 동압의 크기 비( $p' / \bar{p}$ )가 1% 이상일 때로 정의하였고, 과도 응답 상태는 0.2% 이상, 1.0% 미만일 때로 정의하였다.

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F1.jpg

Fig. 1.

Schematic of single can type gas turbine combustor and nozzle assembly with installation location of sensors.

Table 1.

Summary of experimental conditions

Component	Value
Sampling frequency, kHz	10
Static pressure, kPa	150
Air mass flow rate, kg/s	1.334
Inlet temperature, °C	445
Equivalence ratio	0.451~0.539
$H_{2}$ ratio $\frac{H_{2}}{H_{2} + C H_{4}}$ , vol%	0~55

2.2 동압 신호 데이터 처리

2.2.1 신호 처리 구간 설정

동압 신호에 대한 분석을 진행하기 위해서는 분석할 신호 구간의 길이를 정해야 하며, 이 과정을 Fig. 2와 Fig. 3에 순차적으로 나타내었다. Fig. 2는 신호 구간의 길이 선정 과정에 대한 이해를 돕기 위해 10 초 동안 계측한 동압 신호 데이터 중 특히, 연소 상태 진단을 위해 관심 영역으로 볼 수 있는 천이(transition) 상태 발생 직전 1 초(4.5, 5.5) 동안의 신호 구간을 나타낸 것이다.

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F2.jpg

Fig. 2.

Arbitrary dynamic pressure signal data measured for 10 seconds.

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F3.jpg

Fig. 3.

Sliced dynamic pressure signal for an arbitrary period.

다음으로, Fig. 3은 선택된 신호 구간의 동압 신호에 대한 분석을 위해 임의로 선택한 데이터의 길이인 0.02 초를 구간(5.00, 5.02)에 적용 및 확대하여 나타낸 것이다. 분석 대상 길이인 0.02 초 동안에 존재하는 이산 동압 신호 데이터의 개수는 200 개이며, 나머지 신호 구간 역시 같은 길이를 갖도록 분할된다. 다음의 2.2.2.절에서는 분할 된 구간에서 연속된 이산 동압 데이터가 보이는 크기 패턴을 분류하기 위한 경우의 수 계산 방법을 설명하였다.

2.2.2 파형 패턴 경우의 수 분석

파형 패턴(waveform pattern)의 분석을 위해서는 앞서 2.2.1.절에서 나타낸 분석 대상 신호 내에서 크기 패턴을 비교할 연속된 데이터의 개수 즉, 부분집합 당 데이터의 개수( $k$ )를 정해야 하며, 이 값은 크기를 비교하기 위한 최소 개수인 2개부터 선언할 수 있다. 본 연구에서 해당 값은 선행 연구[11]로부터 얻어진 값인 4로 선택하였으며, 이에 해당하는 요소(elements)들은 $\{p'_{i}, p'_{i + 1}, p'_{i + 2}, p'_{i + 3}\}$ 와 같다. 이로부터, 크기 패턴을 비교할 수 있는 경우의 수(number of cases)는 Table 2와 같이 24가지(₄P₃=24)로 계산된다. Fig. 4는 Fig. 3에서 선택한 신호 구간 내에서 부분집합 당 데이터의 개수를 4개로 취하여 패턴 분류를 진행한 예시를 나타낸 것이다. 그림의 좌측부터, 연속된 이산 동압 신호 데이터는 Table 2와 비교했을 때, 각각 case(1), case(18), case(21)로 분류된다. 이외에, 선택한 신호 구간 내에서 아직 분류하지 못한 나머지 부분집합들은 앞서 설명한 것과 같이 각각 Table 2에 정리된 case와 비교하여 해당하는 파형 패턴으로 분류할 수 있다.

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F4.jpg

Fig. 4.

Example cases of waveform pattern on a sampled period.

Table 2.

Details of pattern classification $(k = 4)$

Number of cases	$_{k} P_{k - 1}$
Case	(1)	$p'_{i} \geq p'_{i + 1} \geq p'_{i + 2} \geq p'_{i + 3}$
	(2)	$p'_{i} \geq p'_{i + 1} \geq p'_{i + 3} \geq p'_{i + 2}$
	(3)	$p'_{i} \geq p'_{i + 2} \geq p'_{i + 1} \geq p'_{i + 3}$
	(4)	$p'_{i} \geq p'_{i + 2} \geq p'_{i + 3} \geq p'_{i + 1}$
	…
	(18)	$p'_{i + 2} \geq p'_{i + 3} \geq p'_{i + 1} \geq p'_{i}$
	…
	(21)	$p'_{i + 3} \geq p'_{i + 1} \geq p'_{i} \geq p'_{i + 2}$
	…
	(24)	$p'_{i + 3} \geq p'_{i + 2} \geq p'_{i + 1} \geq p'_{i}$

Fig. 4와 Table 2를 통해 기술한 24가지 case들은 패턴이 서로 중첩되는 경우의 수가 존재하며 즉, 패턴이 중첩되는 case들은 하나의 중첩 패턴으로 분류할 수 있다. 다음 2.2.3.절의 Table 3에 이를 구분 및 분류하는 방법을 나타내었다.

Table 3.

Label definition

A	Case	(1), (24)
	Description	increase	increase	increase
	Description	decrease	decrease	decrease
B	Case	(2), (5), (6), (7), (9), (10), (15), (16), (18), (19), (20), (23)
	Description	increase	increase	decrease
		decrease	increase	increase
		increase	decrease	decrease
		decrease	decrease	increase
C	Case	(3), (4), (8), (11), (12), (13), (14), (17), (21), (22)
	Description	increase	decrease	increase
	Description	decrease	increase	decrease

2.2.3 진단 인자 도출

연소 상태 진단 인자의 도출을 위해서는 앞서 얻은 24가지의 파형 패턴들이 갖는 특성을 정량화하는 과정이 필요하며, 이를 위해 본 연구에서는 각각의 파형 패턴 중 서로 중첩되는 case들을 하나로 묶어 Table 3과 같이 3가지의 대표 패턴(label A, B, C)으로 나타내는 처리 과정을 수행하였다. 우선, 대표 패턴 label A에 해당하는 파형은 부분집합 내 연속된 4개의 동압 크기가 지속적으로 증가(증가→증가→증가) 혹은 감소(감소→감소→감소)하는 파형 패턴들의 집합(see Table 3)이며 이에 해당하는 패턴은 각각 case(1)과 case(24)이다. 다음으로 대표 패턴 label B는 파형 패턴으로 부분집합화된 4개의 동압의 크기가 label A와 달리 구간 내에서 1회의 변곡점을 갖는 유형으로, “증가→증가→감소”, “증가→감소→감소”, “감소→감소→증가”, 또는 “감소→증가→증가”가 이에 해당하며, 예시를 Table 3 B에 나타내었다. 마지막으로, 대표 패턴 label C는 부분집합 내의 4개의 동압 구간 내에서 상대적 크기 비교 시 2회의 변곡점이 존재하는 파형으로써, “증가→감소→증가” 또는 “감소→증가→감소”의 두 가지 경우가 이에 해당하며, Table 3 C에 해당 파형 패턴을 정리하여 나타내었다.

정리하면, 24가지의 파형 패턴은 그 특성에 따라 Table 3에서와 같이 3가지의 대표 패턴(본 연구에서는 label A, B, C로 정의)으로 나타낼 수 있다. 다음의 3장에서는 연소 상태 진단을 위해 정량화 과정을 거쳐 얻은 3가지의 대표 패턴이 동압 신호가 각각 안정, 천이, 불안정 상태일 때 보이는 값의 추세에 대해 분석을 진행하였고, 이를 토대로 각 진단 인자의 특징을 살펴보았다.

3. 진단 성능 분석

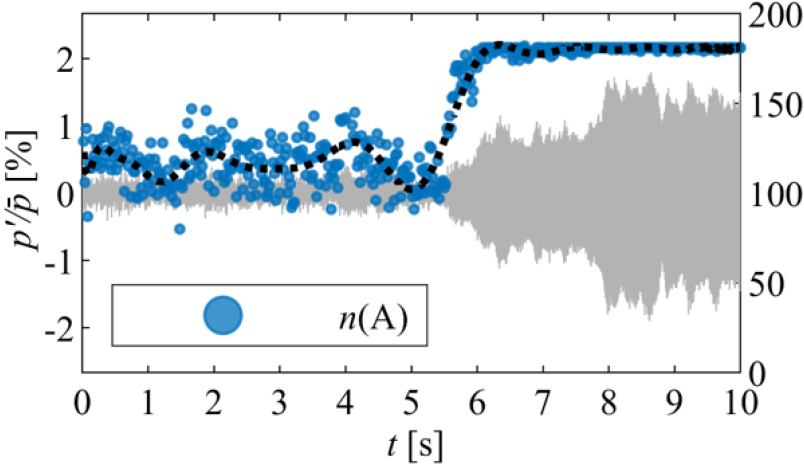
연소 진동이 발생한 동압 신호에 대해 파형 패턴 분류를 통해 도출된 진단 인자인 대표 패턴(label A, B, C)이 정해진 시간 구간 동안 나타난 빈도수를 도출하여 Fig. 5, 6, 7.과 Table 4에 정리하였다. 우선 Fig. 5는 일정 길이로 분할한 신호 구간에서, Fig. 4의 case(1)과 같이 4개의 패턴 요소 모두 연속적으로 감소하거나 증가하는 경우인, 분석 구간에서의 label A로 분류된 값들의 빈도수를 $n (A)$ 와 이들의 평균값을 검은색 점선으로 정리하여 나타낸 것이다. $n (A)$ 는 동압 신호가 잡음 상태일 때 80~147 사이의 상대적으로 넓은 분포의 값을 보이다가 신호가 천이할 때 점차 그 값이 일률적으로 증가하기 시작하고, 동압이 과도기를 거쳐서 한계 진동 상태에 근접하게 되면, 179에서 181 사이의 매우 좁은 범위의 값으로 수렴하는 것으로 나타났다. 이러한 추세는 동압 신호가 안정 상태에서 불안정 상태로 천이할 때 신호의 파형이 점차 정현파(sinusoidal wave)에 가까워지는 것에서 비롯된 것이며 즉, $n (A)$ 는 동압 신호의 파형 패턴이 정현파에 가까운 정도를 정량화 해낸 것으로 나타났다.

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F5.jpg

Fig. 5.

Number of classified pattern; n(A).

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F6.jpg

Fig. 6.

Number of classified pattern; n(B).

https://static.apub.kr/journalsite/sites/kosco/2024-029-01/N0590290103/images/kosco_29_01_03_F7.jpg

Fig. 7.

Number of classified pattern; n(C).

Table 4.

Analysis of $n (A)$ , $n (B)$ , and $n (C)$ at stable and unstable regimes, which were determined by cutoff criterion( $p' / \bar{p}$ >1%)

	Stable ( $t$ <5.50)		Transition (5.50≤ $t$ <8.02)		Limit cycle (8.02≤ $t$ )
	Min	Max	Min	Max	Min	Max
$n (A)$	80	147	103	182	179	181
$n (B)$	38	92	15	78	16	18
$n (C)$	3	37	0	16	0	0

다음으로, Fig. 6의 $n (B)$ 는 분할된 신호 구간 내에서 Fig. 4의 case(16)과 같이 label B로 분류된 패턴들의 빈도수를 나타내며, 마찬가지로 $n (B)$ 의 평균을 검은색 점선으로 나타내었다. 이 값은 신호가 안정할 때 label A와 마찬가지로 38~92 사이의 넓은 분포의 값을 갖다가 점차 신호가 불안정해지면서 그 값이 16~18로 매우 좁은 구간으로 수렴하는 경향을 보이는 것으로 나타났다. 즉, 연소 진동이 발생하여 신호가 점차 일정한 주기를 갖는 정현파에 가까워지면 $n (B)$ 가 일정한 값에 수렴하는 것으로 나타났다.

마지막으로, $n (C)$ 는 Fig. 4의 case(21)과 같이 신호의 패턴이 label A, B보다 상대적으로 복잡한 패턴을 보이는 label C로 분류된 패턴들의 빈도수를 나타낸 것이며, 이에 대한 평균을 검은색 점선으로 나타내었다. 이 값은 동압 신호가 안정 상태를 보일 때 3에서 37 사이의 값을 갖다가 점차 신호가 불안정해지면서 0에 수렴하였다. 즉, $n (C)$ 는 동압 신호가 완전한 사인파(sine wave)일 때 존재하지 않았으며, 따라서 $n (A)$ 및 $n (B)$ 와 마찬가지로 공진 발생 진단을 위한 요소로 활용될 수 있는 것으로 나타났다. Table 4는 진단 요소로 정의한 $n (A)$ , $n (B)$ , 그리고 $n (C)$ 값이 동압 진폭에 따라 보이는 분포를 요약한 것으로, Fig. 2에서 예시로 선정한 10초 동안의 동압 신호를 기준으로, 현재의 연구에서는 $p' / \bar{p}$ 의 값이 0.2% 미만일 때를 안정(stable), 0.2%와 1.0% 사이일 때를 천이(transition), 그리고 매우 큰 한계진폭(1% 이상)에 이르는 조건을 불안정(unstable)으로 정의하였다. 표에서 나타나듯이, $n (A)$ , $n (B)$ , 그리고 $n (C)$ 모두 개별적으로 한계진폭 조건에서 각각의 파형 특성에 따라 일정한 수렴값을 가지는 것을 알 수 있을 뿐만 아니라, 특히 $p' / \bar{p}$ 가 1% 이하인 천이 구간에 대해서도 조기에 사전 진단 인자로써의 활용 가능성을 보여주고 있다.

현재의 연구에서는 새로운 연소불안정 조기 진단 기법 개발의 초기 연구로써, 연속된 동압 신호의 파형 패턴(waveform pattern)에 기반하는 동압 분석 방법을 제안하였고, 불안정과 천이 구간에서 연소불안정의 조기 계측 활용 가능성을 타진하였다. 앞선 결과들에서 소개하였듯이, 본 연구에서 제안하는 진단 인자인 $n (A)$ , $n (B)$ , $n (C)$ 는 개별적으로도 조기 진단의 요소로써 의미가 있으며, 세 가지 요소 간의 특성과 장점들을 결합할 경우 더욱 안정적이면서 빠른 진단 성능을 갖는 연소 상태 진단 모델의 개발이 가능할 것으로 판단된다. 이를 위한 후속 연구로, 세 가지 진단 인자의 특성을 결합하기 위해 딥러닝을 적용한 진단 모델 개발 연구가 진행 중이며, 향후 연구 결과를 통하여 소개될 예정이다.

4. 결론 및 향후 계획

본 연구는 가스터빈 연소기에서 연소 진동의 발생 사전 모니터링을 위한 진단 기법 개발의 기초 단계로, 연소실의 덤프면에서 계측한 이산 동압 신호를 임의의 길이로 일정하게 분할하고, 분할된 각각의 신호들에 대해 파형 패턴 분석을 진행하였다. 분석 과정은 분할된 신호 구간에서, 24가지의 크기 패턴에 기반해 연속된 동압 신호 데이터를 분류하고, 이 중에서 서로 중첩되는 패턴들을 같은 패턴으로 분류하는 순서로 진행되었으며, 최종적으로 3가지(label A, B, C)의 대표 패턴 즉, 진단 요소들을 추출하였다. 각 구간 내 진단 요소들의 빈도수( $n (A)$ , $n (B)$ , $n (C)$ )는 동압 신호가 안정 상태일 때 비교적 넓은 범위에서 분포하다가 동압이 점차 불안정해지면 일정 값에 수렴하는 경향을 보이는 것으로 나타났다. 이러한 경향성으로부터 선행 연소불안정 조기 진단 과 마찬가지로, 현재 연구에서 제안하는 파형 패턴 분석 기법 역시 연소 진동의 발생을 안정적으로 사전에 진단하는 도구로써 활용할 수 있는 가능성이 확인되었다. 이뿐만 아니라, 이 기법은 동압 신호가 과도 상태일 때 역시 효과적으로 진단할 수 있는 성능을 갖고 있는 것으로 나타났다.

이러한 초기 연구 결과를 기반으로, 후속 연구에서는 딥러닝 모델을 활용하여 3가지의 진단 요소들이 보이는 각각의 성능을 결합 및 연소 상태 진단 모델로의 개발을 진행할 예정이다.

Acknowledgements

본 연구는 2024년도 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원으로 수행된 연구 결과(RS-2023-00254668)입니다.

References

H.W. Kim, U.H. Jin, Y.G. Go, M.J. Choi, I.Y. Gu, M.H. Baek, K.T. Kim, Shin, D, A Review of Carbon Neutral Gas Turbine Combustion Technology, Journal of The Korean Society of Combustion, 27(2) (2022) 14-38. 10.15231/jksc.2022.27.2.014

D.S. Han, J.M. Seok, J.H. Park, B. Emerson, T. Lieuwen, Doosan Combustion Auto Tuning (DCAT) System for H-Class Gas Turbines, 62th KOSCO Symposium, 2021, 121-122.

V. Panov, Auto-Tuning of Real-Time Dynamic Gas Turbine Models, Proceedings of ASME Turbo Expo, 2014. 10.1115/GT2014-25606

D. Noble, L. Angello, S. Sheppard, J. Kee, B. Emerson, T. Lieuwen, Investigation into advanced combustion system health monitoring, Proceedings of the ASME Turbo Expo, 2019. 10.1115/GT2019-91973

Z. Feng, M. Liang, F. Chu, Recent advances in time-frequency analysis methods for machinery fault diagnosis: A review with application examples, Mechanical Systems and Signal Processing (2013) 38(1) 165-205. 10.1016/j.ymssp.2013.01.017

D. Noble, T. Lieuwen, Advanced Gas Tur- bine Combustor Health Monitoring Using Combustion Dynamics Data, 59^th ISA POWID/EPRI Symposium, 2016.

W.J. Song, D.J. Cha, Temporal kurtosis of dynamic pressure signal as a quantitative measure of combustion instability, Appl. Therm. Eng., 104 (2016) 577-586. 10.1016/j.applthermaleng.2016.05.094

S.P. Joo, J.W. Choi, N.K. Kim, M.C. Lee, Zero-crossing rate method as an efficient tool for combustion instability diagnosis, Exp. Thermal Fluid Sci., 123 (2021). 10.1016/j.expthermflusci.2020.110340

J.W. Choi, O. Choi, M.C. Lee, N.K. Kim, On the observation of the transient behavior of gas turbine combustion instability using the entropy analysis of dynamic pressure, Exp. Therm Fluid Science, (2020) 115. 10.1016/j.expthermflusci.2020.110099

J.J. Hwang, M.K. Kim, W.J. Lee, K.W. Min, D.W. Kang, H.S. Kim, Combustion Characteristics of Axial Fuel Staging Nozzles for Gas Turbine Combustors, J. Korean Soc. Combust., 28(4) (2023) 21-29. 10.15231/jksc.2023.28.4.021

S.K. Choi, D.S. Kim, Diagnosis of Comb- ustion Instability in Gas Turbine Combustor Using Auto-Encoder-Based Machine Learning, The KSFM J. Fluid. Machinary., 27(1) (2024) 49-56. 10.5293/kfma.2024.27.1.049

Journal of The Korean Society Combustion ISSN:1226-0959(Print) 2466-2089(Online) 한국연소학회지

Preview

Diagnosis of Combustion Instability Using Waveform Pattern of Dynamic Pressure Signal

ABSTRACT

MAIN

Fig. 1.

Schematic of single can type gas turbine combustor and nozzle assembly with installation location of sensors.

Table 1.

Summary of experimental conditions

Fig. 2.

Arbitrary dynamic pressure signal data measured for 10 seconds.

Fig. 3.

Sliced dynamic pressure signal for an arbitrary period.

Fig. 4.

Example cases of waveform pattern on a sampled period.

Table 2.

Details of pattern classification(k=4)

Table 3.

Label definition

Fig. 5.

Number of classified pattern; n(A).

Fig. 6.

Number of classified pattern; n(B).

Fig. 7.

Number of classified pattern; n(C).

Table 4.

Analysis of n(A), n(B), and n(C) at stable and unstable regimes, which were determined by cutoff criterion(p'/p¯>1%)

Acknowledgements

References

Details of pattern classification $(k = 4)$

Analysis of $n (A)$ , $n (B)$ , and $n (C)$ at stable and unstable regimes, which were determined by cutoff criterion( $p' / \bar{p}$ >1%)