1. 서 론

환경규제가 점차 강화되면서 온실가스 배출량 감축에 대한 요구가 증가함에 따라 친환경적인 발전용 가스터빈의 중요성이 높아지고 있다[1]. 연소 과정에서 발생하는 질소산화물(NOx) 배출 규제로 인하여, 최근 가스터빈 연구는 운전 단계별 NOx 배출 저감을 위한 연소 기술 개발에 집중하고 있다.

컴퓨터를 이용한 전산 해석 기술이 발전함에 따라 전산유체역학(CFD)을 활용한 다방면의 정보 생성 기능이 중요한 연구 도구로 활용되고 있다[2]. 그러나 산업 부문에서 대부분의 연소 현상은 난류 조건에서 일어나므로 반응 시스템 해석의 복잡성을 야기한다. 채택된 반응 모델에 따라 연소 성능 예측의 정확성이 좌우된다.

Spalding[3]의 Eddy break-up 모델을 기반으로한 eddy dissipation(ED) 모델은 예혼합 및 비예혼합 연소에서 광범위한 적용 가능성을 보여주었다[4]. 이후, 지속적인 연구를 통해 유한 속도 화학반응을 고려한 standard eddy dissipation concept(EDC) 모델로 확장되었다[5]. 여기서 화학반응은 유체의 반응 부분을 나타내는 미세 구조 내부의 완전 교반 반응기 조건에서 일어난다. 그러나 단순화된 모델은 복잡한 화학 시스템을 완전히 설명할 수 없었다[6]. 또한, MILD 연소 시스템에서의 화염 온도 및 화학종 프로파일을 예측하는 접근 방식이 불가능하다[7].

Partially stirred reactor(PaSR) EDC 모델은, 난류 조건에서 완전히 혼합된 상태가 아니며, 부분적으로 혼합되거나 혼합되지 않은 영역이 존재함을 고려한 모델이다. 즉, 이러한 현상을 고려하여 혼합 및 화학반응이 포함된 난류 화학 상호작용 모델로 활용되고 있다.

본 연구에서는, 가스터빈 모형 연소실에서 EDC 모델에 따라 압력 변화에 따른 NOx 배출 경향성을 파악하고자 수치해석을 수행하였다.

2. 수치해석 방법

2.1 모델 형상 및 격자

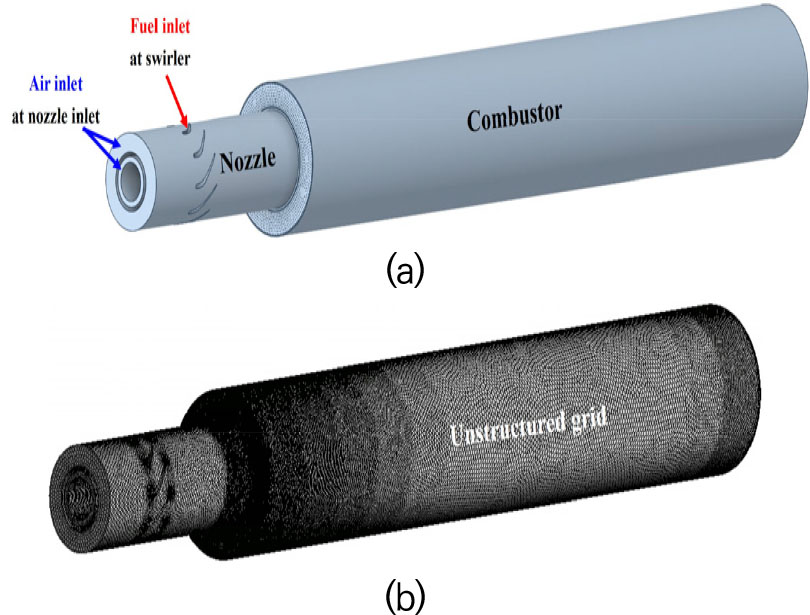
가스터빈 모형 연소실의 형상 및 격자를 Fig. 1에 나타내었다. 노즐 입구에 공기가 주입되며 선회기(swirler) 지점의 연료 홀을 통해 연료가 주입되고, 공기가 선회기 지점에 도달하여 연료와 혼합이 시작되는 부분 예혼합 방식을 채택하였다.

Fig. 1.

(a) Geometry and (b) mesh grids of a model combustor installed with a nozzle.

수치해석에 사용한 격자는 polyhedral 형상으로 unstructured gird로 구성하였으며, 노즐 부분의 격자 수는 약 300 만개, 연소기 부분의 격자 수는 약 87 만개이다. 공기와 연료의 입구 유동영역, 화염 형상을 관찰하기 위한 노즐 출구와 연소기 전반부에는 상대적으로 격자를 조밀하게 형성하였다.

2.2 경계 조건

수치해석 경계조건을 Table 1에 나타내었다. 공기와 연료의 온도는 각각 718 K, 283 K로 설정하였다. NOx 배출량을 평가하기 위해 압력을 1.3 bar(상압), 21 bar(고압)에 대해 두 가지 EDC 모델의 비교 및 검증을 수행하였다. 압력을 증가시킬 때 노즐 입구(공기 입구 영역에 위치함) 속도를 고정하였고 이에 따라 공기 및 연료 유량은 압력에 비례하여 증가하였다. 질량 유량을 Table 2에 나타내었다.

2.3 지배방정식

수치해석을 위해 3차원 정상상태의 지배방정식을 RANS (Reynolds averaged Navier Stokes) 방정식으로 변환하였다. 난류 모델은 연료와 산화제간 혼합 과정을 모사하기 위해 SST k-ω 모델을 사용하였으며, 편미분 방정식의 공간적 이산화를 위해 2^nd order upwind scheme을 적용하였다. 화학종 방정식을 풀이하였고, NO 생성 경로에 해당하는 Zeldovich(또는 thermal), Fenimore, N₂O 중간 생성물 그리고 NNH 메커니즘까지 모두 포함된 GRI 3.0을 채택하였다[8,9]. 본 연구에서는 범용 열유체 해석 코드인 ANSYS Fluent 2023 R2를 사용하여 수치해석을 수행하였다[10].

2.4 EDC 모델

수치해석에 사용된 지배방정식 중 화학종 보존방정식은 다음과 같다.

여기서 식 (1)의 Ri은 화학반응에 따른 화학종 i의 총 생성률을 의미한다. 식 (2)의 Ri항에 포함된 매개변수중 𝜌는 밀도, τ*는 반응 영역의 체류 시간, Yi0는 초기 화학종 i의 질량 분율, Yi*는 반응 영역에서 화학종 i의 질량 분율, 그리고 𝜅은 반응 영역의 질량 분율을 나타낸다.

𝜅와 τ*를 구하는 방법에 따라 다양한 EDC 모델이 제시되어 있다.

2.4.1 Standard EDC 모델

여기서, 식 (3)의 ξ*는 길이 스케일로, 𝜅는 길이스케일의 비로 나타낸다. 식 (4)의 ξ*항에 포함된 매개변수중 𝜈는 동점성계수, k는 난류 운동 에너지, 𝜀는 난류 소산율을 나타낸다.

Standard EDC 모델은, 느리게 형성되는 오염물질인 NOx 형성에 대한 예측을 정확하게 할 수 없다는 한계를 가지고 있다. 이는 𝜅와 τ*항에 포함된 매개변수 중 화학 및 혼합 시간이 명시적으로 포함되어 있지 않기 때문이다.

2.4.2 PaSR EDC 모델

여기서, 식 (6)의 tchem는 화학반응 시간, tmix는 혼합 시간, 식 (7)의 Damko¨hler 수(Da)는 화학반응 시간과 혼합 시간의 비를 나타낸다. 식 (8)의 tchem항에 포함된 매개변수 중 ωi는 화학종 i의 반응률을 의미한다. 식 (10)의 Cmix는 국소 난류 레이놀즈 수(ReT)의 함수로 구성된 혼합 상수를 의미하며, Cμ는 k-ε 난류 모델의 상수를 나타낸다. 그리고 지수 계수인 𝛼는 식 (11)와 같이 표시되며, 프랙탈 차원 D = 3일 경우, 난류유동에 있어 가장 작은 스케일인 kolmogorov 마이크로스케일인 반면, D = 5일 경우, 난류유동에서 큰 에디들로 구성된 적분 스케일(또는 난류 매크로 스케일)을 의미한다. 본 연구에서는 적분 스케일로 가정한다(Cmix = 1).

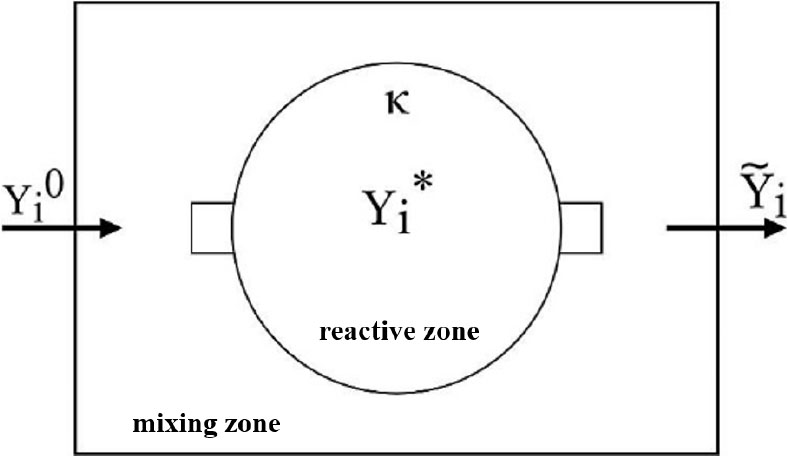
PaSR EDC 모델은 Fig. 2와 같이 반응 영역과 혼합 영역으로 구분되어 있는 부분 교반 반응기 조건에 적합하다. 반응 및 혼합 영역 간 물질 교환은 시스템의 화학 및 혼합 시간 척도의 함수로 표현되는 인자(𝜅, τ*)에 의해 결정되며 Yi~(화학종 i의 최종 평균 질량 분율)을 통해 포괄적인 난류 화학적 상호작용을 고려할 수 있다[12]. (𝜅, τ*, Yi0, Yi*식 (2) 참조)

Fig. 2.

Concept of the PaSR model[11].

3. 결과 및 논의

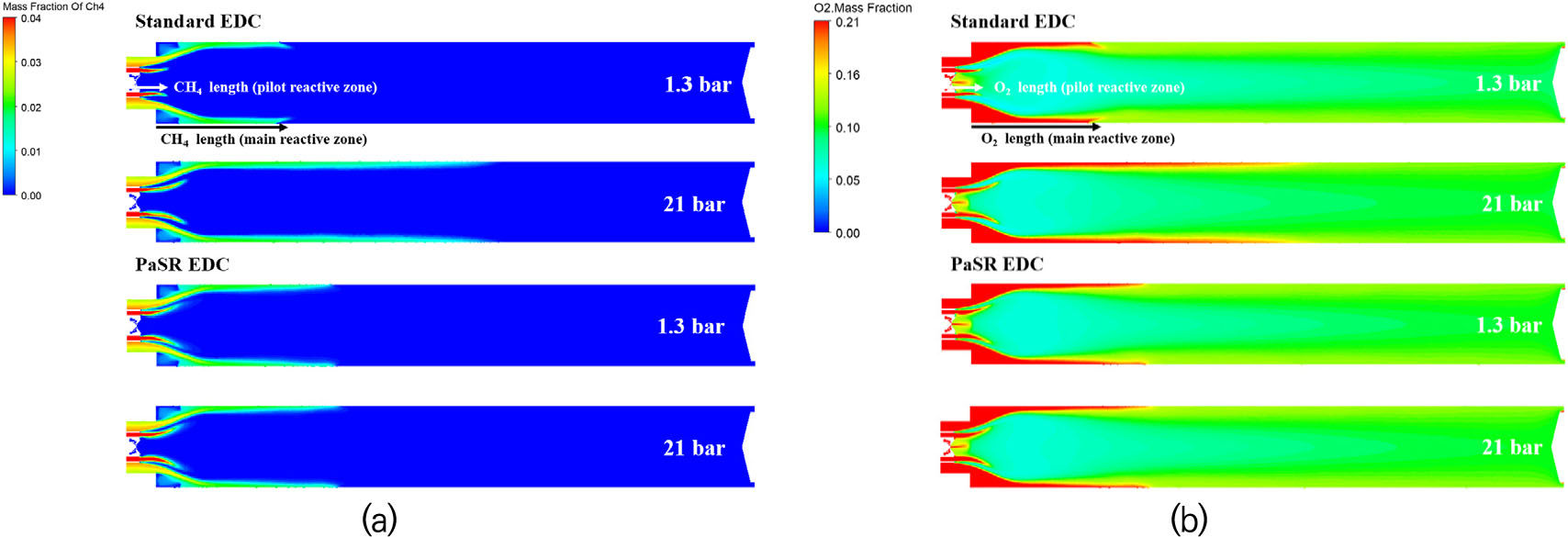
EDC 모델 선택에 따른 계산 결과를 상호 비교하고 검증하기 위해 가스터빈 모형 연소기를 대상으로 수치해석을 수행하였으며, 연소기 내부의 연료와 산화제 농도를 파악하기 위해 메탄과 산소 질량 분율을 Fig. 3에 나타내었다. Standard EDC 모델 적용시, 압력이 증가함에 따라 반응 지역(메인 및 파일럿 경로)에서 메탄과 산소가 존재하는 영역의 길이가 증가한다. 이는 압력을 증가하였을 때 연료 및 공기의 공급 속도가 소모되는 속도보다 크기 때문이다. 반면, PaSR EDC 모델 적용시, 압력이 증가하더라도 메탄과 산소 영역의 길이는 동일하다. 즉, 고압 조건(21 bar)에서도 공급되는 연료 및 공기 유량이 혼합 및 화학반응 과정에 영향을 끼침을 알 수 있다.

Fig. 3.

Mass fraction fields of (a) CH₄ and (b) O₂ predicted by the two EDC models at various pressure.

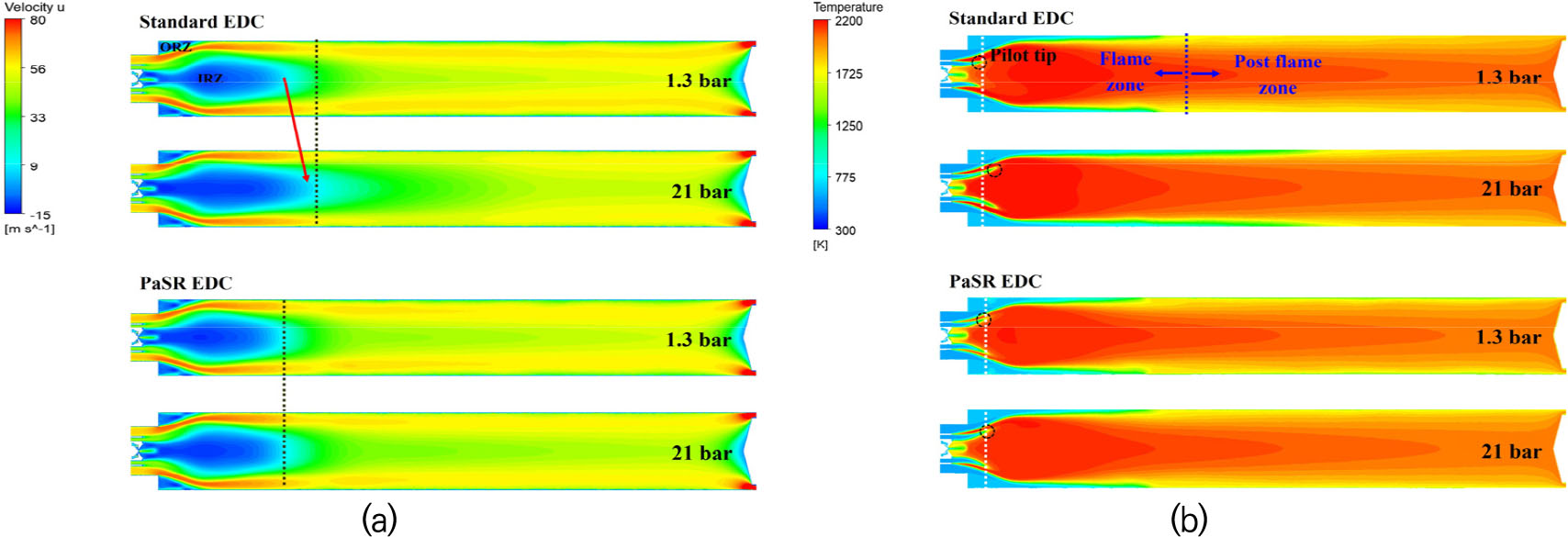
Fig. 4에 연소기 내부의 속도장과 온도장을 나타내었다. 선회기 지점에서의 선회 유동에 의해 생성되는 inner recirculation zone(IRZ)은 고온의 화염 형성 및 화염 안정성이 향상되는 역할을 한다. Outer recirculation zone(ORZ)은 노즐 출구에서 연소기 입구 지점과 같이 유동 면적이 급격히 확대될 때, 연소기 corner 부근에서 역 압력 구배가 생기며 형성된다. 연소기 상류 지점에 해당하는 화염 지역(flame zone)에는 IRZ에 의해 고온이 형성되며, 연소기 벽면에서는 화염 온도가 상대적으로 감소한다. 그 이유는 속도가 음의 영역인 ORZ에 의해 반응물이 분포하기 때문이다. 그러나 post flame zone에서 ORZ는 감소하여 화염 온도가 상대적으로 증가함을 알 수 있다. Standard EDC 모델 선택시, 압력이 증가할 수록 IRZ와 파일럿 반응 영역 길이가 증가하는 반면 PaSR EDC모델에서는 동일한 것을, 파일럿 팁 위치 변화를 통해 검증할 수 있다.

Fig. 4.

(a) Velocity and (b) temperature fields of the combustor at various pressures (two EDC models adopted).

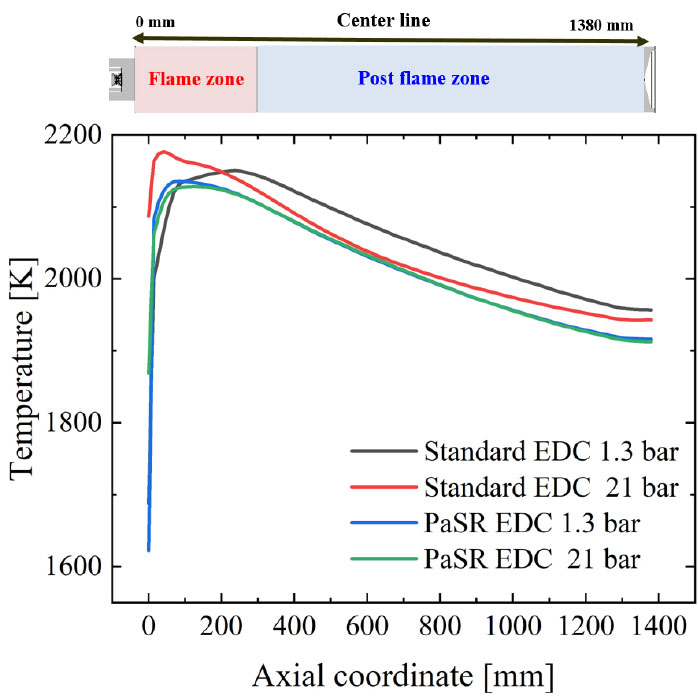
Fig. 5에서 보듯이, 화염지역에서는 공기와 연료간 혼합 및 화학반응에 따라 온도가 급격히 증가하는(약 1600 ~ 2200 K) 반면, post flame zone에서는 축 위치 변화에 따라 온도가 점진적으로 감소하였다(약 1900 ~ 2150 K). Standard EDC 모델 선택시, 압력 증가에 따라 온도의 평균 감소율은 0.6%이며, PaSR EDC 모델 대비 온도가 소폭 증가하였다.

Fig. 5.

Temperature profiles along the center line in the combustor at various pressures (two EDC models adopted).

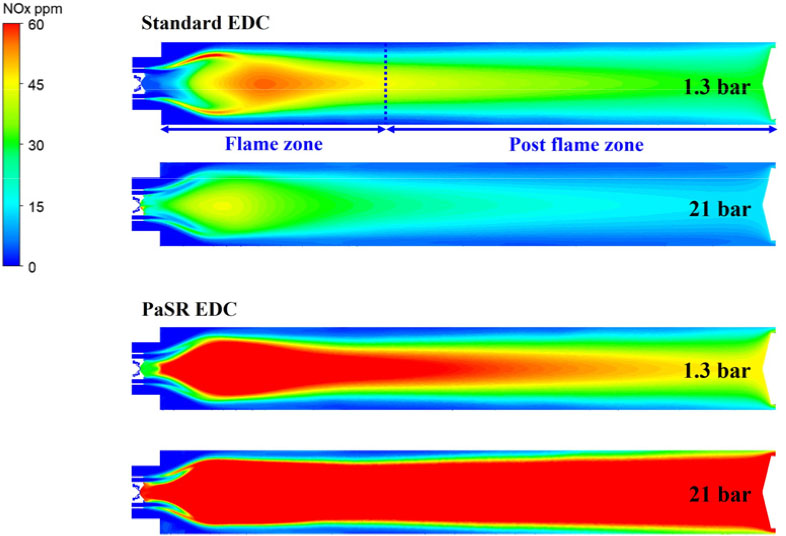
Fig. 6에 연소기 내부의 NOx 배출 분포를 나타내었다. EDC 모델에 따른 연소실 단면에서의 NOx 배출 농도를 상압과 고압 조건에서 나타냈다. Standard EDC 모델 선택시, 압력에 따라 NOx 배출 농도는 화염지역에서 post flame zone 까지 감소한 반면, PaSR EDC 모델에서는 증가함을 파악하였다.

Fig. 6.

NOx emission fields of the combustor at various pressures (two EDC models adopted).

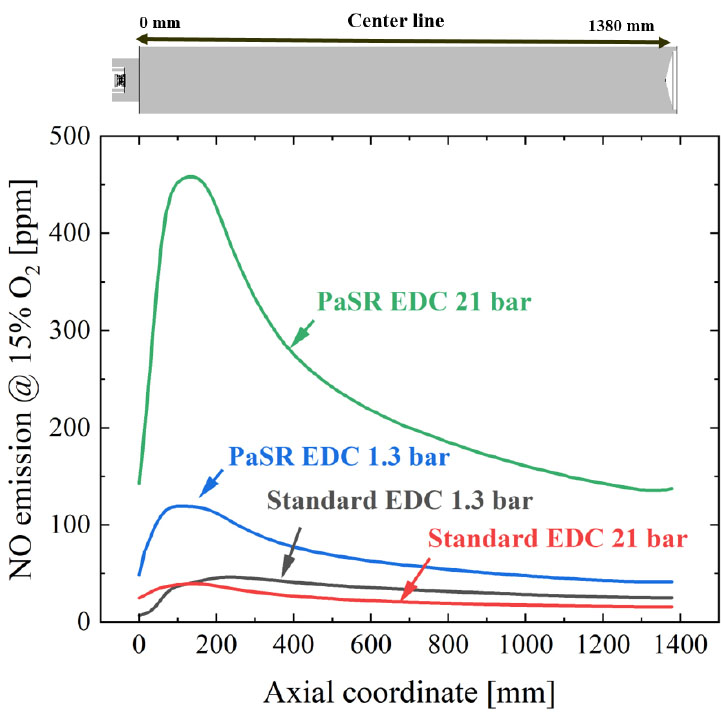
Fig. 7에 나타낸 연소실 입구부터 출구 지점까지 NOx 배출 프로파일을 비교한 결과, 압력 변화에 따라 Standard EDC 모델에서는 평균 NOx 배출량이 약 5.87 ppm으로 소폭 감소하였다. 그러나, PaSR EDC 모델은 평균 NOx 배출량이 약 37 ppm으로 대폭 증가함을 예측하였다. 이는, Standard EDC 모델이 𝜅, τ*항으로 압력 효과에 따른 동역학적인 NOx 형성 과정을 정확히 예측하지 못함을 보여준다. 그러나 PaSR EDC 모델은 화학반응 및 혼합 시간 매개변수를 통해 NOx 배출 정확도를 향상시킬 수 있었다.

Fig. 7.

NOx concentration profiles along the center line in the combustor at various pressures (two EDC models adopted).

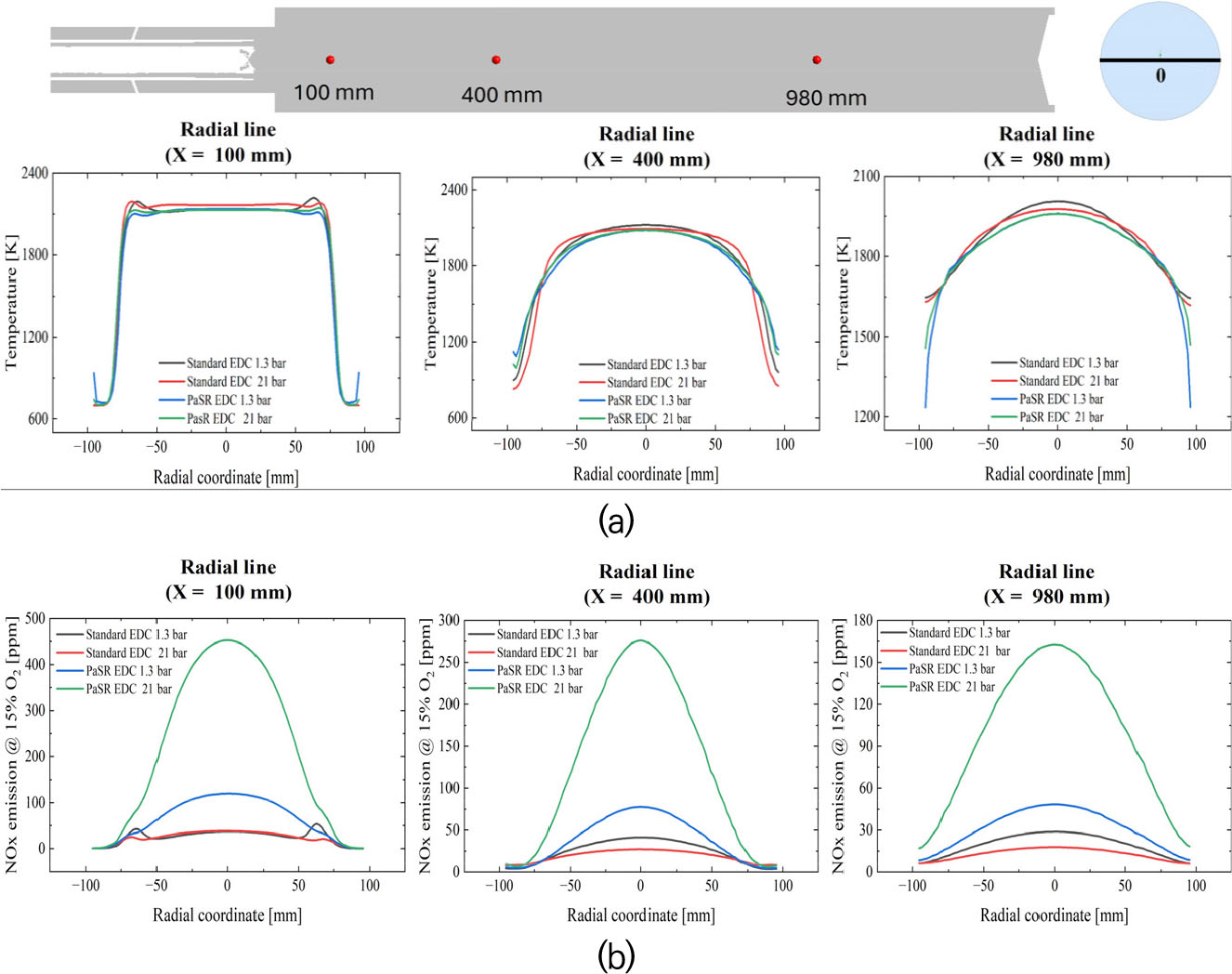
연소실 단면의 축 위치 변화(x= 100, 400, 980 mm)에 따른 온도 및 NOx 배출 변화를 Fig. 8에 나타내었다. Standard EDC 모델 선택시, 압력 변화에 따른 온도와 NOx 배출 농도 변화는 미미하다. PaSR EDC 모델의 경우, 압력 변화에 따른 평균 온도 증가율이 약 0.67%이었으며, 평균 NOx 배출 증가율은 약 70%로 큰 폭으로 증가하였다. 이는 EDC 모델 선택에 있어, 온도는 NOx 배출의 주요 매개변수가 아님을 암시한다.

Fig. 8.

Profiles of (a) temperature and (b) NOx emission in the combustor along the radial line at various axial positions.

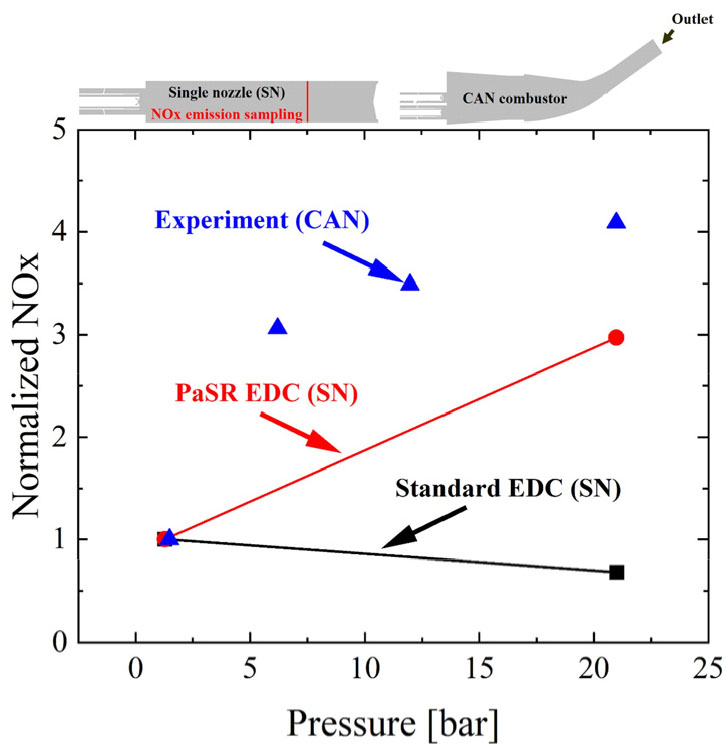
Fig. 9의 상압에서 고압 조건까지 EDC 모델에 따른 싱글 노즐을 장착한 모형 연소기의 수치해석 NOx 결과와 실 스케일 기반인 싱글 노즐의 집합체인 CAN 연소기의 NOx 실험 결과를 비교하였다. 싱글 노즐의 NOx 샘플링 농도 계측 지점에서 측정한 결과, 압력이 증가함에 따라 Standard EDC 모델은 소폭 감소하였다. 그러나 PaSR EDC 모델의 경우, 대폭 증가하였다. 이는 CAN 연소기 출구에서 측정한 NOx 실험 결과와 동일한 경향성을 보여주었기에 PaSR EDC 모델은 Standard EDC 모델과 비교하여 NOx 형성에 정확도를 갖는 EDC 모델임을 입증한다.

Fig. 9.

Result of NOx emission : numerical analysis of a single nozzle (two EDC models adopted) and experiment from a CAN combustor.

4. 결 론

본 연구에서는, 실 스케일의 가스터빈 모형 연소실에서 EDC 모델 선택에 따른 압력 효과에 의한 NOx 배출 특성을 파악하기 위해 수치해석을 수행하였다. 상압(1.3 bar) 및 고압(21 bar) 조건에서 노즐 속도를 고정한 상태에서 연료 및 공기 유량을 설정하였다. Standard EDC 모델 선택시, 연소실 입구에서 출구 지점까지 압력 변화에 따른 NOx 배출 농도를 계산한 결과, 약 5.87 ppm으로 소폭 감소하였다. 그러나 PaSR EDC 모델 선택시 약 37 ppm으로 대폭 증가하였다.

Standard EDC 모델 선택시, 연소실 단면에서 축 위치 변화에 따라 압력 증가에 의한 온도 및 NOx 배출 농도 차이는 미미하다. 그러나 PaSR EDC 모델의 경우, 온도와 달리 NOx 배출량이 큰 폭으로 증가하였다. 이는 EDC 모델 선택에 있어 온도는 NOx 배출의 주요 매개변수가 아님을 암시한다.

연소해석을 위한 지배방정식 중 화학종 보존방정식에 포함된 매개변수 Ri항에 포함된 𝜅, τ*는 EDC 모델에 따라 정의하는 방식이 다르다. 느리게 형성되며 동역학적으로 지배적인 기체 오염물질인 NOx 형성을 예측할 때, Standard 모델 대비 화학 및 혼합 시간 매개변수가 포함된 PaSR EDC 모델이 좀 더 높은 예측 정확도를 보인다.이는 압력이 증가함에 따라 NOx 배출이 증가하는 경향성을 갖는 CAN 연소기 실험 결과를 기반으로 신뢰성을 입증할 수 있다.

후속 연구에서는 매개변수인 Cmix 변화에 따른 혼합 시간이 NOx 배출에 미치는 영향을 검증할 예정이다.