1. 서 론

열음향 시스템의 연소 과정에서는 압력 섭동과 열 방출률 섭동이 상호간에 에너지를 전달하는 순환이 이루어진다[1]. 이러한 에너지의 전달 과정에서 열 방출률 섭동과 압력 섭동의 위상차가 90° 이내가 되는 레일리 기준(Rayleigh’s criterion)을 만족했을 때, 에너지가 증폭되어 열음향적 자려진동(self-sustained oscillation)이 발생하고 시스템의 상태 불안정이 촉발되는 것으로 알려져 있다[2]. 최근 환경 규제로 인해 NOx 배출 저감에 유리한 희박 예혼합 조건의 운전이 선호되는 추세이나, 이러한 조건에서는 국부적인 당량비 변화로 인해 위와 같은 연소 불안정 현상의 발생 가능성이 높다[3]. 연소 불안정 현상의 발생 양상은 연소 시스템의 작동 조건과 형상 등 다양한 물리적 변수의 영향을 받는데, 불안정 발생 시 높은 열에너지에 의해 열응력과 기계적 부하가 증가하여 시스템의 변형과 파괴를 불러올 수 있고, 화염 날림과 역화 현상 등 연소 시스템의 동작 이상을 유발할 수 있다[3]. 따라서, 연소 시스템에서의 열음향적 불안정 현상에 대한 분석, 예측 및 회피가 주요한 연구 주제로서 관심받고 있다[4,5,6,7,8].

익히 알려진 바와 같이 단일 노즐이나 적은 수의 노즐을 가지는 연소기에서의 연소 불안정성은 많은 경우 연소 시스템의 종방향(longitudinal) 음향 모드와 결합하여 발생한다[9]. 이는 로켓 연소실과 같이 연소실 후단의 노즐에서 추력을 발생시키는 경우 원통형 연소기 형상이 선호되기 때문이다[10]. 그러나, 발전용 가스터빈이나 현대의 항공 엔진 연소기는 환형 혹은 캔-환형의 구조를 가지는 경우가 많다. 종횡비가 1과 유사한 이러한 형태의 연소기에서는 접선(tangential) 및 반경(radial) 모드 등이 결합하여 횡방향(tra- nsverse) 모드 혹은 방위 방향(azimuthal) 모드 등 복잡한 형태의 불안정성이 발생할 수 있으며, 이러한 모드가 유발하는 고주파에서의 불안정성은 저주파 모드에 비해 위험성이 높은 것으로 보고되고 있다[11]. 이와 같은 이유로 상당수의 실험적 및 수치적 연구에서 환형 연소기의 불안정성에 대한 분석을 수행하였다. 실험적으로는 반경 방향의 다중 압력센서를 통한 위상차 분석 기법이 중점적으로 활용되었으며, 대칭성 파괴 등을 통해 불안정성을 제어하는 방법이 제시되었다[12,13,14]. 수치적으로는 헬름홀츠 방정식의 수치해 및 열음향 네트워크 모델 등으로 모드 간 상관관계를 분석하는 연구가 수행된 바 있다[15,16]. 이러한 연구를 포함하여 환형 연소기에서의 동특성에 관한 포괄적인 리뷰는 Vignat et al. [10]의 저술을 참조할 수 있다.

본 연구에서는 위와 같은 선행 연구와 유사한 맥락에서 환형 모사 가스터빈 연소기의 동특성을 분석하며, 여기서 나아가 해당 연소기에서의 소음 기반 동역학(Noise-Induced Dynamics)적 특성을 연구하고자 한다. 연속 연소 시스템은 유동 불안정성, 화학 반응과 열 방출률의 섭동 및 기타 외란 등으로 다양한 소음에 노출되어 있는데[17], 이러한 소음은 [18]에 정리된 바와 같이 소음 기반 동역학적인 효과를 유발하여 시스템에 대한 추가적인 정보를 잠재적으로 제공할 수 있다. 예를 들어, 소음으로 인한 가진을 활용하여 연소 시스템의 안정성 여유를 평가하거나[3, 19], 시스템의 선형 및 비선형 인자를 추출하는 연구[20,21,22,23]가 수행된 바 있다. 이러한 관점에서, 본 연구에서는 환형 연소기의 열음향적 동특성을 분석하는 한편, 해당 연소기를 확률적으로 가진(stochastic forcing) 함으로써 추가적으로 확인할 수 있는 시스템 특성에 대해 연구하고, 이를 통해 연소 시스템의 열음향적 불안정에 대한 진단분석에 기여하고자 한다.

2. 연소시험 및 검증

2.1 실험장치 구성 및 시험 조건

본 연구에서 사용한 환형 모사 가스터빈 연소기 실험 장치의 개략도를 Fig. 1에 나타내었다. 연소기는 내경 395 mm, 외경 405 mm의 환형 형상으로, 내부 벽면을 제외하고 SUS304 재질로 제작되었으며, 내부는 화염 영상에 대한 광학적 관측을 위해 원통형으로 가공된 쿼츠로 제작하였다. 연소기 내부에는 직경 35 mm와 스월 수 0.608을 가지는 단일 노즐을 통해 유동이 공급되도록 하였다. 연소기 상부에는 직경 60 mm를 가지는 원형 출구를 9개 설치하였으며, 노즐 상부에는 내측 254 mm, 외측 400 mm의 부채꼴 형태 유동 출구를 별도로 설치하여 연소기의 과열을 방지하였다.

Fig. 1.

Schematic diagram of the annular m odel gas-turbine combustor experime ntal setup equipped with a loud sp eaker for transverse stochastic forcing. MFC: Mass Flow Controller.

연소 실험을 위한 연료로는 순도 95.95%의 메탄을 사용하였고, 산화제로는 압축기(Kyungwon AL5N)를 통해 압축한 압축 공기를 사용하였다. 연료와 산화제 유량은 각각 MKP TSC-230, MKP TSC-145의 질량 유량계를 통해 조절하였으며, 압축 공기는 드라이어(Kyungwon T15K)를 사용하여 수분을 제거하였다. 연료와 산화제는 확장-수축관에서 1차 예혼합 과정을, 선회류 발생 장치(swirler)를 지나며 2차 예혼합 과정을 거쳐 노즐을 통해 연소실로 공급되도록 설계되었다. 연소기 내부의 압력 측정을 위해 노즐 출구에서 수직으로 50 mm 이격된 지점에 동압 센서(PCB Piezotronics Model 113B28)를 설치하였으며, 온도 계측을 위해 연소기의 원주 방향으로 45° 간격마다 총 8개의 K-type 열전대(Omega KMQSS-125E-6)를 설치하였다. 횡방향의 음향 소음을 활용한 가진을 위해 연소기의 측면에 스피커(Sammi ME-250B100)를 설치하였으며, 여기에 입력되는 백색 가우스 신호는 신호 발생기(Keysight 33210A)에서 발생시켜 증폭기(LTO MAC 2.2)를 통해 증폭되도록 하였다. 또한, 화염 영상 관측을 위해 최대 960 fps의 영상 계측이 가능한 캠코더(Sony FDR-AX700)를 연소기 측면에 설치하였으며, 두 장의 평면거울을 통해 Fig. 1과 같이 연소기 내측으로부터 화염 영상을 계측할 수 있도록 하였다.

연소실험은 연료와 산화제의 전체 유량을 5.5 g/s로 일정하게 유지하는 조건에서 당량비를 변화시키며 수행하였다. 당량비는 희박 화염 날림(lean blowoff)이 발생하지 않은 최솟값인 0.74부터 0.9까지 0.02 간격으로 변화시켰다. 소음 기반 동역학적 특성을 확인하기 위해 각 조건에서 백색 가우스 잡음 신호를 0-9 Vpp의 입력 신호 세기로 스피커를 통해 공급하였다. 각 당량비 조건에서는 상기한 캠코더를 통해 120 fps로 화염 영상을 계측하였다. 본 연구에서 사용한 연소실험 조건은 Table 1에 정리하였다.

2.2 음향 모드 해석

위 2.1절에서 기술한 환형 모사 가스터빈 연소기의 열음향적 특성 분석을 위해 음향 모드 해석을 수행하였다. 모드 해석은 음향 특성에 주요한 영향을 미치는 연소기와 스피커를 대상으로 수행하였으며, 연소기와 스피커 외벽을 음향 경계(Sound hard boundary wall) 조건으로 설정하여 경계면에 작용하는 파동의 영향을 무시하였다. 이러한 조건에서 연소기에 대한 헬름홀츠 방정식(Helmholtz equation)의 수치해를 상용 수치해석 프로그램인 COMSOL Multiphysics V6.1을 활용하여 계산하였다.

해석 결과 Fig. 2에 나타낸 바와 같이 다양한 음향 모드가 관찰되었다. 우선 Fig. 2(a)와 같이 186.7 Hz의 스피커 연결부의 음향 모드가 관찰되었으며, 이어서 연소기 자체의 음향 모드로써 Fig. 2(b, c)와 같이 각각 356.9 Hz, 363.4 Hz의 횡방향 모드가 관찰되었다. 또한, 499.3 Hz에서의 반경 방향 모드인 Fig. 2(d)와 535.7 Hz의 종방향 모드인 Fig. 2(e)가 식별되었다. 종합적으로, 음향 모드에 대한 수치해석을 통해 350-550 Hz의 좁은 범위 내에서 연소기의 횡방향, 종방향 및 반경 방향의 음향 모드가 다양하게 나타남을 확인하였다.

Fig. 2.

Acoustic modes of the annular model gas-turbine combustor identified from the numerical simulations (COMSOL Multiphysics V.6.1).

3. 결과 및 분석

3.1 연소기 검증 및 분기 해석

위 2.1절에 기술한 조건에서 환형 모사 가스터빈 연소기의 연소 실험을 통해 주파수 분석을 수행하였다. 각 당량비 조건에서 연소기의 음향 모드에 따라 Fig. 3과 같이 파워 스펙트럼 밀도에 뚜렷한 피크 값이 관찰되었는데, 이 중 다수는 음향 모드 수치해석 결과에 부합하였다. 구체적으로, 180.1 Hz의 스피커 연결부 모드와 354.8 Hz, 365.1 Hz의 횡방향 모드, 484.8 Hz의 반경 방향 모드 및 540.2 Hz의 종방향 모드가 주파수 해석을 통해 확인되었다. 이중 횡방향 모드로 식별된 354.8 Hz와 365.1 Hz에서의 섭동은 주파수 스펙트럼상 주변 기저에 비해 높은 에너지 밀도를 가지는 것으로 확인되어 열음향 섭동에 주요한 영향을 미칠 것으로 예측되었다.

Fig. 3.

Power spectral density of the pressure fluctuations in annular model gas-turbine combustor at the equivalence ratio of 0.86.

이어서, 당량비 변화에 따라 주파수 해석에서 식별된 각 모드에서의 압력 섭동이 변화하는 양상을 확인하였다. 각 모드별 압력 섭동은 Fig. 3에 표기된 주요 5개 모드에 대해 주파수 공간에서 대역폭 10 Hz의 대역 필터(bandpass filter)를 동압 신호에 적용함으로써 분리하였고, 이후 힐베르트 변환(Hilbert transform)을 통해 섭동의 진폭을 계산하였다. 이러한 방식으로 산출한 모드별 섭동 진폭 변화를 Fig. 4에 나타내었다. 우선, Fig. 4(a)에 표시된 180.1 Hz 모드는 당량비 증가에 따라 압력 섭동이 대체로 증가하는 추세를 보였으며, 다른 모드에 비해 강한 섭동 에너지를 가진 것으로 확인되었다. 그러나 해당 주파수가 나타내는 스피커 연결부의 음향 모드는 연소기 자체의 형상으로 인한 것이 아니며, 본 연구에서 소음 가진을 위해 설치한 스피커가 부재한 경우 연소동역학적인 영향을 미치지 못하므로 실제적인 연소 불안정 측면에서 물리적 의미가 적어 추가적인 해석이 불필요하다고 판단하였다. 354.8 Hz에서의 횡방향 모드는 Fig. 4(b)와 같이 당량비 𝜙=0.8과 𝜙=0.82 사이에서 특징적인 분기 현상이 확인되었다. 분기 이전에는 5 Pa 내외의 미약한 압력 섭동만이 관측되었으나, 이후 초임계 호프(supercritical Hopf) 형태의 분기에 이은 수 배의 섭동폭 증가가 관찰되었다. 따라서, 이러한 관찰 결과를 바탕으로 다음 절에서 해당 주파수에서 소음 기반 동역학적 해석을 추가로 수행하고자 하였다. 365.1 Hz와 484.8 Hz에서의 압력 섭동은 당량비 변화에 따라 유의미한 차이를 보이지 않았으며, 종방향 모드인 540.2 Hz에서는 당량비가 𝜙=0.8 이상으로 증가되는 시점에 약간의 섭동 진폭 증가가 관찰되었으나 그 세기가 미미하였다. 전체적으로 볼 때, 당량비 증가에 따라 압력 섭동폭의 점진적인 증가가 확인되었으며, 이는 Fig. 5와 같이 화염 강도의 증가와 함께 화염면의 가시적인 섭동을 동반하였다.

Fig. 4.

Mean amplitude of the pressure fluctuation at each oscillation mode identified in Fig. 3. X-axis indicates the methane-air equivalence ratio.

Fig. 5.

Images of the lean-premixed swirled flame at varying equivalence ratios obtained via a high-speed camera.

3.2 소음 기반 동역학적 해석

서론에 언급된 바와 같이, 연소 시스템을 소음으로 가진함으로써 얻을 수 있는 주요한 결과 중의 하나는 확률적 시스템 식별(stochastic system identification) 기법을 통한 시스템의 선형, 비선형 변수 추출 및 이를 바탕으로 한 연소 불안정성 평가이다. 연소 불안정의 발달을 나타내는 초임계 호프 분기 인근에서 시스템이 소음에 의해 가진되는 경우, 압력의 섭동이 자려진동의 형태로 거동함을 가정하여, 압력 섭동(x)의 시간(t)에 따른 변화를 다음과 같이 반 데르 폴(Van der Pol) 진동자 모델에 우변 확률항을 추가하여 나타낼 수 있으며[20]:

여기서 𝜖은 선형 변수, α1은 비선형 변수이고 ω는 섭동 각주파수, d는 소음 강도, 𝜂는 단위 소음항을 나타낸다. 위 모델에서 선형 변수가 음수이면 열음향적 안정 상태, 양수이면 한계 순환 형태의 불안정성을 나타내므로, 𝜖이 음에서 양으로 변화하는 시점에 분기가 발생한다. 따라서, 적절한 시스템 식별 기법을 통해 데이터로부터 𝜖, α1 등의 변수를 추출하여 연소 시스템의 상태 진단에 활용할 수 있음이 알려져 있다. 확률적 시스템 식별 방법은 [24] 등이 제안한 수학적 기법을 기반으로 개발되었으며, 열음향 섭동[20, 22]뿐 아니라 유체역학적 섭동[25,26] 및 플라즈마 섭동[27] 등 다양한 시스템에서 검증된 바 있다. 이러한 기법은 데이터로부터 추출한 섭동 진폭의 확률밀도함수 또는 조건부 확률을 수학적 모델(Eq. 1)로부터 유도된 포커-플랑크 방정식(Fokker-Planck equation, [28])과 일치시킴으로써 수행된다. 본 논문에서는 이 기법과 관련된 수학적 방법에 대한 기술을 생략하며, 구체적인 방법론은 [29]을 참고할 수 있다.

Fig. 6(a)에 재차 나타낸 354.8 Hz에서의 압력 섭동에 대한 확률적 시스템 식별 결과를 Fig. 6(b)와 (c)에 나타내었다. 확률적 시스템 식별은 0보다 큰 소음 환경에서 계측된 데이터를 필요로 하므로, 환형 모사 가스터빈 연소기를 스피커를 통해 0-9 V 세기로 무작위 확률 가진한 상태에서 계측한 압력 섭동 데이터로부터 시스템 식별을 수행하였다. 섭동 진폭 관찰 결과와 부합하게 선형 변수(𝜖)가 0.8<𝜙<0.82 범위에서 음에서 양으로 변화하는 것을 확인하였으며, 이 시점에서 열음향적 불안정성이 발생함을 수학적으로 재확인하였다. 또한, 연소 불안정성의 발생과 함께 비선형 감쇠 변수(α1)의 절대값이 감소하는 것을 관찰할 수 있었다. 추출된 결과에서 𝜖은 선형 추세, α1은 멱함수 추세를 따르는 것을 확인하였는데, 이러한 관계식은 선행 연구에서 보고된 관계식[25,29]과 일치하였다. 따라서, 연소기의 소음 가진을 통해 확률적 시스템 식별을 수행하여 열음향 섭동 측면에서 상태 진단을 수행할 수 있음을 확인하였다.

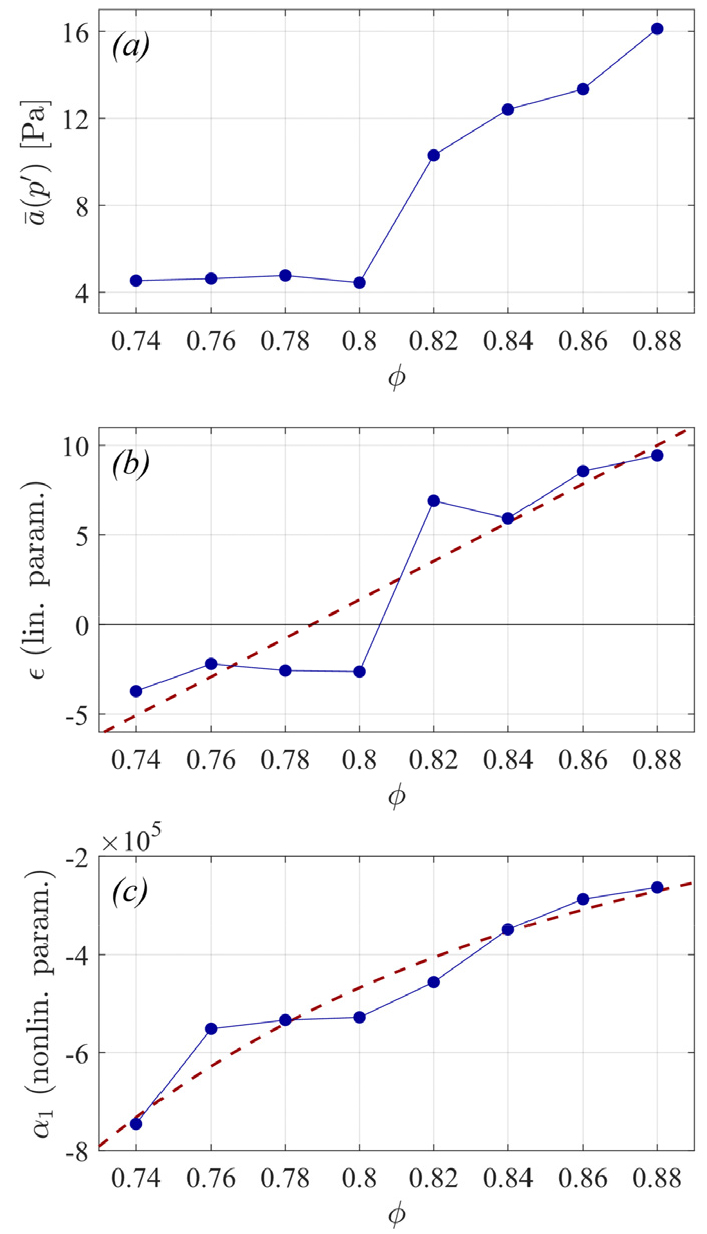
Fig. 6.

(a) Bifurcation diagram of the transverse mode oscillation at 354.8 Hz under varying equivalence ratios, and (b) linear / (c) nonlinear system parameters of the same oscillation. Red dashed lines indicated (b) linear and (c) power-law fitting of the linear and nonlinear system parameters, respectively.

마지막으로, 소음 세기에 따른 코히어런스 공진(coherence resonance, [30,31]) 효과를 분석하였다. 코히어런스 공진은 시스템의 신호가 소음에 의해 증폭되는 현상을 지칭하며, 중간 정도 세기의 소음에서 최대의 공진이 나타나는 것으로 알려져 있다[31]. 이는 소음이 미약한 경우 공진을 발생시 에너지가 부족하고, 소음이 지나치게 강한 경우 무작위적 특성이 시스템의 동특성을 지배하기 때문이다. 코히어런스 공진은 일반적으로 분기 직전에 가장 잘 관찰되며, 공진을 통해 분기 이후의 동특성을 분기 이전에도 관찰할 수 있으므로, 연소 불안정의 전구적 현상으로 기능할 수 있다[18]. 나아가, 이러한 특성을 활용하여 열음향적 자려진동에 대한 시스템 식별을 수행하여 연소 불안정의 발생을 예측하는 데에도 코히어런스 공진 현상을 활용할 수 있음이 알려져 있다[22,23,32].

Ushakov 등[33]은 공진의 강도를 주파수 피크의 높이와 너비의 비율인 코히어런스 지수(coherence factor, 𝛽)로 수치화하였는데, 상기한 바와 같이 소음 세기의 증가에 따라 𝛽값이 증가 후 감소하는 양상을 보임을 보고하였다. Fig. 6(a)와 같이 분기하는 횡방향 모드에서, 분기 발생 직전인 𝜙=0.8에서 코히어런스 지수를 산출한 결과 Fig. 7의 결과를 획득하였다. 𝛽값이 소음 가진 세기의 증가에 따라 증가하다가 5-6 V 인근에서 최대를 보인 후 감소하는 양상을 관찰하여 환형 연소기의 횡방향 모드에 대한 코히어런스 공진 특성을 확인하였다. 이러한 결과를 바탕으로 중간 세기의 소음 가진을 통해 분기 이전의 시스템에서도 분기 이후의 열음향 섭동에 대한 정보를 효과적으로 추출할 수 있을 것으로 판단되었다.

Fig. 7.

Coherence factor of the 354.8 Hz thermoacoustic mode at 𝜙=0.8 and varying noise intensities. Red dashed line indicates a regression line using the Gaussian function.

4. 결 론

본 연구에서는 모사 가스터빈 연소기에서 메탄-공기 예혼합 화염의 동특성을 분석하였으며, 스피커를 활용하여 해당 연소기를 횡방향으로 가진하여 소음 환경에서 연소 시스템의 소음 기반 동역학적 거동을 평가하였다. 연소실험을 통해 수치해석 결과와 부합하는 열음향 모드를 확인하였으며, 이중 354.8 Hz로 섭동하는 횡방향 모드의 당량비 변화에 따른 초임계 분기 현상을 관찰하였다. 해당 모드에 대해 연소기를 소음으로 가진함으로써 확률적 시스템 식별을 수행하여 시스템의 선형 및 비선형 변수를 추출하였고, 이러한 변수의 거동으로부터 열음향 섭동 측면에서 연소기의 상태 진단을 수행할 수 있음을 확인하였다. 또한, 소음 가진으로 관측된 코히어런스 공진 현상을 이용하여 열음향 분기 이후의 동특성을 분기 이전에도 관찰할 수 있음을 제시하였다. 이러한 결과를 바탕으로 향후 본 연구에서 적용된 것과 유사한 인위적인 소음 환경을 조성하여 환형 연소기를 포함한 연소 시스템의 소음 기반 동역학적 거동을 유발하여 연소기의 진단 및 동특성 예측을 수행할 수 있을 것으로 기대된다.

기 호 설 명

α1 : Nonlinear system coefficient

𝛼 : Oscillation amplitude

𝛽 : Coherence factor

d : Noise intensity

𝜖 : Linear system coefficient

p' : Pressure oscillation

𝜂 : Unit Gaussian noise

PSD : Power spectral density

ω : Oscillation angular frequency

Vpp : Peak-to-peak voltage

𝜙 : Equivalence ratio