Comparisons of Flame Stretch Calculation Models and Their Applications Part I: Model Comparisons

Yong Jea Kim; Dong-hyuk Shin

doi:10.15231/jksc.2023.28.2.022

Preview

Technical Notes

Journal of the Korean Society of Combustion. 30 June 2023. 22-37
https://doi.org/10.15231/jksc.2023.28.2.022

Comparisons of Flame Stretch Calculation Models and Their Applications Part I: Model Comparisons

화염 스트레치 계산 모델들의 비교와 적용 I: 모델 비교

Yong Jea Kim¹

Dong-hyuk Shin¹^†

김 용제¹

신 동혁¹^†

¹Department of Aerospace Engineering, Korea Advanced Institute of Science and Technology

¹한국과학기술원 항공우주공학과

^{*Corresponding Author}

ABSTRACT

Invariant forms of the flame stretch on three dimensional flame surfaces were derived by M. Matalon (1983), S. H. Chung and C. K. Law (1984), and S. M. Candel and T. J. Poinsot (1990) respectively in different forms. To resolve potential confusions, the three model forms were compared, and their mutual identities were described in this study. The respective model equations were also organized in their decomposed expressions, by normal and tangential stretch components and by components induced by flow velocity and flame speed. Their applications into numerical and experimental data were discussed, and potential application issues were addressed by illustrating flame stretch calculation procedures. In most situations, necessary parameters (e.g., flame location, migration velocity, flame speed, flow velocity, etc.) could be extracted from the data on the flame surface. Some model equations require operations covering outside of the flame surface, which could be unknowns to calculate flame stretch.

Keywords

Flame stretch

Flame curvature

Flame speed

MAIN

1. 서 론
2. 화염 스트레치 산출 모델 식 비교
2.1 화염 스트레치 산출 모델 식
2.2 모델 식들의 비교
3. 화염 스트레치의 분해 표현식
3.1 화염 거동에 따른 스트레치 분해 표현 식
3.2 유동 속도와 화염 전파 속력에 따른 스트레치 분해 표현 식
4. 화염 스트레치 모델 식 적용의 이론적, 수치적, 실험적 접근의 비교
4.1 화염 면의 정의
4.2 화염 면 단위 법선 벡터 설정 및 적용
4.3 화염 면의 곡률 산출
4.4 화염 이동 속도, 유동 속도, 화염 전파 속력의 적용 및 화염 스트레치 산출
5. 결 론

1. 서 론

연소 성능 개선, 공해 가스 배출 저감 등의 연소기의 성능 개선이나, 친환경 수요에 따른 새로운 연료를 사용하는 연소기 개발 등을 위해서(산화제와의 혼합을 포함한) 연료의 연소 특성에 관한 연구가 필요하다. 연료의 연소 특성 중, 화염의 형상, 거동, 전파 및 이동 속도 등의 화염의 동역학적 특성들은 연소실 내 연소 및 유동 현상에 영향을 미친다. 화염의 형상 또는 분포 특성은 연소실 내의 연소 환경 변화에 영향을 미치므로, 연소 효율, NOx, CO 등 공해 가스 생성 등에 영향을 미친다[1]. 또한, 시-공간적으로 변화하며 섭동하는 화염의 동역학적 특성들은 화염 및 유동 현상에 영향을 미치며, 역화(flash back), 국소 소염(local extinction), 화염 날림(blow out), 연소불안정(combustion instability) 등의 발생과 연관이 있다[2,3].

화염의 형상, 거동, 이동 및 전파 등의 동역학적 특성을 연구하기 위한, 화염 면의 거동의 대표적인 운동학적 특성들로는 화염 전파 속력 $s_{L}$ , 화염 면 이동 속도 ${\vec{v}}_{f}$ , 화염 면의 곡률 𝜅, 화염 스트레치 $K$ , 등이 있으며, 연료의 종류, 혼합 연료의 혼합비, 산화제, 당량비 등의 연료 특성에 따라 영향을 받게 된다. 이러한 특성들의 관계를 연소-유동 현상을 조사하여 규명 및 모델링하는 많은 연구들이 진행되어왔다[4,5,6,7].

이러한 연구들을 위하여 앞서 언급한 화염 면의 운동학적 특성들을 명확하게 정의하고 정확하게 측정하거나 산출하여야 한다. 화염 면을 정의하고, 화염 면의 형상 및 위치를 구하고, 화염 전파 속력 $s_{L}$ , 화염 면 이동 속도 ${\vec{v}}_{f}$ , 화염 면의 곡률 𝜅, 화염 스트레치 $K$ 등을 구하여야 한다. 화염 면의 정의는 등온선(isotermal line)을 이용하여 예가열 구간(preheat zone), 반응 구간(reacting zone) 등에서 설정하거나[8], 특정 화학종의 분포를 이용하여 설정하는[9,10,11] 등 여러 방법들이 사용되고 있다. 또한, 화염 면의 이동 속도 (또는 화염 전파 속력과 화염 면의 비반응 유동 속도 정보)를 구하기 위하여, 정의된 화염 면을 추적하여[12] 화염 면의 이동 속도을 산출하거나, 화염 및 유동장의 데이터를 고려하여 화염의 전파 속력을 구하는 등 다양한 방법이 사용되고 있다[8]. 본 연구에서는 화염 이동 속도 또는 화염 전파 속력 산출과 화염 면 정의 방법은 다루지 않으며, 화염 면 데이터를 이용하여 모델을 이용한 연산이 요구되는 화염 스트레치(및 곡률) 산출에 관하여 조사하였다.

화염 스트레치 개념은 B. Karlovitz[13]에 의해 처음 고려되었으며, F. A. Williams[14,15]에 의해 일반화되었다. 이동하는 미소-화염 면 요소(infinitesimal flame surface element)의 시간에 따른 변화율로 아래 식 (1)과 같이 나타난다.

(1)

K = \frac{1}{δ A} \frac{d (δ, A)}{d t}

화염 면의 스트레치는 J. Buckmaster[16]에 의해 처음 고려되어 직교 좌표계(cartesian coordinate)에서의 표현식을 얻어내었으며, M. Matalon[17]은 이를 확장하여 일반적인 경우에 적용할 수 있는 불변 형태(invariant form)의 표현식을 구하였다. S. H. Chung and C. K. Law[18]는 화염 면에 접하는 곡선 좌표계(curvilinear coordinate)를 이용하여 화염 스트레치 표현식을 얻었다. S. M. Candel and T. J. Poinsot[19]은 플럭스 수송 정리(flux transform theorem)를 이용하여 텐서 형태의 화염 스트레치 표현식을 구하였으며 본 문서에서 이들을 간략히 소개하였다.

이러한 화염 면의 스트레치 산출에 관한 대표적인 3개의 모델 식들은 서로 상이한 형태와 유도 배경을 갖고 있어 이론적 연구 목적, 수치해석 및 실험 데이터 분석 목적으로 사용할 때 혼동이 발생할 수 있다. 모델 식에 따라, 텐서 또는 벡터 연산 형태의 복잡한 표현식을 갖고 있어 실험 또는 수치해석 데이터 분석 시 적용이 용이하지 않을 수 있다. 화염 스트레치 산출을 이용한 기존의 많은 연구들은 원형 또는 구형 화염(spherical flame)[20,21], 정상 상태(steady) 분젠 화염(bunsen flame)[22], 스테그네이션 포인트 화염(stagnation point flame)[23], 등, 단순화된 화염 면 거동 현상을 다루어 화염 스트레치 산출 및 근본적인 화염의 동역학적 특성을 조사한다. 이 경우, 모델 식들의 일부분만 고려할 수 있으며, 간접적인 방법으로 모델 식들의 항들을 구할 수 있으므로, 전체 모델 식들의 사용이나 모델 식들의 비교는 명확하게 정리되어 있지 않다.

본 연구에서는 앞서 언급한 화염 스트레치 산출을 위한 3개의 모델 식들의 동일함을 묘사하였다. 화염 스트레치 모델 식들의 화염의 거동에 따른 분류와 화염의 이동에 기여하는 요인들을 이용하여 분해한 표현식들을 제공하였다. 화염 스트레치 산출 모델 식들을 이론적 연구 목적이나 수치해석 및 실험 데이터 분석을 위한 목적으로 적용할 때, 특이점과 장단점들을 고찰하였다.

본 연구와 함께 제출한 연구, “모델 적용”[24]에서는 화염 스트레치 산출 모델 식들의 적용에 관하여 논하며, 특히, 수치해석 및 실험을 통해 얻은 화염 및 유동장 데이터를 분석하여 화염 스트레치를 산출하기 위한, 화염 스트레치 모델 식의 적용을 간략히 묘사하였다. 1차원 원형/구형 화염, 2차원 정상 상태(steady) 화염, 2차원 비정상 상태(unsteady) 화염의 화염 스트레치 산출을 위한 명료한 산술식을 제공하였다. 화염 스트레치 산출 예시로 정상 상태의 2차원 층류(laminar) 블러프 바디 화염(bluff body flame)의 화염 스트레치와 비정상 상태의 조화 진동(harmonic oscillation)하는 화염 홀더에 안정화된 층류 V-형상 화염(V-shape flame)의 화염 스트레치를 산출하였다.

2. 화염 스트레치 산출 모델 식 비교

화염 스트레치 산출 모델 식들을 소개하고 유도과정을 간략히 묘사하였다. 화염 스트레치 산출 모델 식들은 각각 유도과정과 배경이 다소 차이가 있으며 서로 다른 형태를 가지고 있다. 이러한 화염 스트레치 산출 모델 식들의 동일함을 묘사하였다.

2.1 화염 스트레치 산출 모델 식

화염 스트레치는, 앞서 언급한 식 (1)과 같이, 이동하는 화염 면의 미소-면 요소의 넓이의 시간 변화율을 나타낸다. 화염 스트레치 산출 모델 식들은, 국소 지점에서의 화염 스트레치를 계산하기 위해, 미소 화염 면 넓이의 시간 변화율을 직접 계산하는 대신, 화염 면의 국소 이동 속도와 화염 면의 기하학적 정보들로부터 화염 스트레치를 산출한다.

이러한 화염 스트레치 계산을 위한 3가지 모델 식들, i) Matalon[17], ii) Chung and Law[18], iii) Candel and Poinsot[19], 에 관하여 아래에 간략히 소개하였다(문헌에 나타난 모델 식들의 변수명, 연산식, 및 기호 표현들은 비교를 위해 적절히 변경하였다.).

3차원 공간에서 화염 면이 각 국소 지점의 화염 이동 속도로 이동할 때, 화염 면의 위치, 방향, 형상(곡률 및 면 요소의 형상)과 넓이가 변화하게 된다. 아래 Fig. 1에 기준 직교 좌표계(reference cartesian coordinate), $(x, y, z)$ ,에 대하여 국소 화염 이동 속도 ${\vec{v}}_{f}$ 로 이동하는 3차원 공간 내 화염 면을 나타내었고, 미소 화염 면을 회색으로 채색하여 나타내었다. 국소 지점에서 미소-면에 접하는 단위 직교 접선 벡터들 $\vec{τ_{1}}, \vec{τ_{2}}$ 와 미소-면에 수직인 단위 법선 벡터 $\vec{n}$ 은 미소-면에 접하는 곡선 좌표계(curvilinear coordinate), $(ξ_{1}, ξ_{2}, η)$ ,의 기저 벡터(basis vector)를 이룬다. 즉, 미소 화염 면은 국소 곡선 직교 좌표계에서 각 변의 길이 $\partial ξ_{1}$ 과 $\partial ξ_{2}$ 로 이루어진 사각형의 면 요소이다(Fig. 1의 회색으로 채색된 부분 참조). 또한, 국소 화염 이동 속도 ${\vec{v}}_{f}$ 는 화염 면에 수직인 성분 ${\vec{v}}_{f, n}$ 과 접하는 성분 ${\vec{v}}_{f, τ}$ 로 나눌 수 있다. 화염 스트레치 산출 모델 식들의 비교를 위한 변수 명의 통일을 위하여, 아래 Fig. 1에 공통으로 사용된 최소한의 변수들을 나타내었다.

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280203/images/ksssf_28_02_03_F1.jpg

Fig. 1.

A schematic of a flame surface showing its curvilinear coordinate system and the reference coordinate system.

2.1.1 Matalon의 모델 식

화염 면 스트레치는 J. Buckmaster에 의해 처음 고려되어 직교 좌표계(cartesian coordinate)에서의 표현식을 얻었으며[16], M. Matalon은 일반적인 경우에 적용할 수 있는 불변 형태(invariant form)의 모델 식을 구하였다[17].

3차원 공간에서 화염 면은 아래의 조건, 식 (2)를 만족하는 점들의 집합으로 표현할 수 있다.

(2)

F (x, y, z, t) = 0

일반적으로 하나의 변수에 관한 국소적으로 명시적인 해를 얻을 수 있다. Fig. 1의 경우, $z$ 에 관한 매개 변수들, $x, y, t$ , 의 함수의 형태로 표현할 수 있다.

(3)

F (x, y, t) - z = 0

M. Matalon은 기준 직교 좌표계 $(x, y, z)$ 에서 위 식 (3)의 화염 면 조건을 이용하여 미소 화염 면 요소의 넓이를 나타내었고, 국소 화염 이동 속도에 의해 화염 면이 변화하며 이동할 때 미소-면 요소의 넓이 변화(식 (1))를 조사하였다.

화염 스트레치를 화염 면의 형상과 화염 이동 속도의 정보를 이용하여, 아래와 같은 모델 식을 얻었다.

(4)

K = - {\{\nabla \times ({\vec{v}}_{f} \times \vec{n})_{F = 0} \circ \vec{n}\}}_{F = 0} - {\{\frac{\partial f / \partial t}{\sqrt{1 + (\partial f / \partial y)^{2} + (\partial f / \partial z)^{2}}} (\nabla \circ \vec{n})\}}_{F = 0}

위 식 (4)에서 아래첨자로 표시된 조건, $F$ =0,은 화염 면을 의미하며( $f (x, y, t) - z = 0$ 조건과 동일함), $f$ 는 식 (3)을 이용하여 화염 면을 정의하는 함수이다. Fig. 1에 나타난 바와 같이, $\vec{n}$ 은 국소 지점에서 화염 면에 수직인 단위 법선 벡터이다. ${\vec{v}}_{f}$ 는 국소 화염 이동 속도이다. 기호 𝛻은 델 연산자이다.

(5)

\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}

Fig. 1과 같이, 국소적으로 $z$ 에 관한 매개 변수들, $x, y, t$ ,의 함수의 형태로 표현된 화염 면의 정의를 일반적인 경우로 확장하여 아래와 같은 화염 스트레치 모델 식을 얻었다.

(6)

K = - {\{\nabla \times ({\vec{v}}_{f} \times \vec{n})_{F = 0} \circ \vec{n} + \frac{\partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n})\}}_{F = 0}

Matalon의 모델 식은 불변 형태(invariant form)로 표현되어 일반적인 화염 면의 형상에 적용할 수 있도록 하였다. 위의 식 (6)으로부터 화염 면 위에서의 화염 이동 속도와 형상 정보를 이용하여 화염 스트레치를 구하는 것을 알 수 있다.

그러나, 연산의 경우 화염 면에 이웃한 영역의 화염 면 밖에서의 정보를 요구할 수 있다. 수학적 이론 모델 전개에서는 가능할 수 있으나, 대부분의 실험이나 수치해석의 경우 현시간 화염 면과 화염 면 위의 정보만 제공되며 화염 면 밖의 정보들은 정의와 확보가 불분명할 수 있다. 예를 들어, 델 연산자( $\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}$ )의 경우 $x, y, z$ 방향으로 미분을 계산할 때, 화염 면 위의 정보와 더불어 화염 면 밖의 정보를 요구할 수 있다. 좌표 변환을 통해 화염 면의 곡선 좌표계 $(ξ_{1}, ξ_{2}, η)$ 에서 델 연산자( $\nabla = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}} + \vec{n} \frac{\partial}{\partial η}$ )를 사용하더라도 $\vec{n} \frac{\partial}{\partial η}$ 미분 항이 화염 면 밖의 정보를 요구한다. 비슷한 이유로, $\nabla \circ \vec{n}$ 항을 계산하기 위해 발산 연산(divergence)을 수행할 때 화염 면 밖의 정보를 요구할 수 있는데 화염 면에 수직인 단위 벡터 $\vec{n}$ 은 화염 면 위에서만 정의되므로 연산을 수행하기 위해서는 추가 조건이 필요하다(면-발산(surface divergence) $\nabla_{s} \circ \vec{n}$ 을 이용해 계산 가능하며, 본 문서의 “화염 면의 곡률 산출” 부분에서 논의한다.).

또한, 연산을 위해 현시간 외 현시간 전후의 화염에 관한 정보를 요구할 수 있다. 식 (6)의 두 번째 항의 $\frac{\partial F / \partial t}{| \nabla F |}$ 는 화염 형상 함수 $F$ 의 시간 과 공간 변화 정보가 요구된다. 시간 미분 $\partial F / \partial t$ 의 수학적 또는 수치적 수행을 위해서는 국소 지점에서의 현시간 전후의 화염 형상 함수 $F$ 가 필요하다. 그러나, 화염 형상 함수 $F$ 는 현시간과 국소 지점에서 식 (2)와 같이 $F$ =0로 정의되어 있으며, 시간에 대한 부분 미분을 위한 고정된 국소 지점에서의 현시간 전후의 화염 형상 함수 $F$ 와 화염 면의 정의는 불분명하다. 또한, $\nabla F$ 항을 계산하기 위해 기울기-벡터 연산(gradient)을 수행할 때 화염 면 밖의 정보를 요구할 수 있는데 화염 형상 함수 $F$ 는 화염 면 위에서만 정의되므로 연산을 수행하기 위해서는 추가 조건이 필요하다.

한편, 식 (6)의 두 번째 항의 $\frac{\partial F / \partial t}{| \nabla F |}$ 의 연산은 이러한 문제들을 우회하도록 고려할 수 있다. 화염 이동 속도 ${\vec{v}}_{f}$ 와 화염 면 정의 함수 $F$ 는 아래와 같은 조건, 식 (7)을 만족한다.

(7)

v_{f, n} = {\vec{v}}_{f} \circ \vec{n} = \frac{- \partial F / \partial t}{| \nabla F |}

위 식 (7)의 $v_{f, n} (= {\vec{v}}_{f} \circ \vec{n})$ 을 살펴보면, 국소 지점에서 화염 면에 수직인 단위 법선 벡터 $\vec{n}$ 은 화염 면에서 식 (2)와 같이 정의된 화염 면 형상 함수 $F$ 를 이용해 아래와 같이 정의된다.

(8)

\vec{n} = \frac{\nabla F}{| \nabla F |}

위 식 (8)에서는 화염 면에 수직인 단위 법선 벡터 $\vec{n}$ 을 구하기 위해, 화염 면과 화염 면 밖의 화염 면 형상 함수 $F$ 에 관한 기울기-벡터 연산 수행을 이용하지만, 이를 대신하여, 현시간 화염 면의 기하학적 정보만을 이용하여 화염 면에 수직한 단위 벡터를 구할 수 있다.

따라서, 화염 면의 형상 만을 이용하여 구한 단위 법선 벡터 $\vec{n}$ 과 위 식 (7)을 화염 스트레치 모델 식, 식 (6)에 적용하면, 연산을 위해 현시간 외 화염 면 형상 함수 $F$ 의 정보가 필요한 문제를 우회할 수 있다(그 외의 모델 식, 식 (6)의 적용에 관한 내용은 후에 자세히 논의한다.).

2.1.2 Chung and Law의 모델 식

Matalon의 모델 식 유도[17]와 유사한 방법을 사용하였으며, S. H. Chung and C. K. Law는 특히, 화염 면의 곡면을 따르는 곡선 직교 좌표계(curvilinear coordinate)를 이용하여 간결하고 명료한 유도를 꾀하였다[18].

미소 화염 면 요소의 국소 지점에서의 넓이를 미소-면 요소에 접하는 곡선 직교 좌표계 $(ξ_{1}, ξ_{2}, η)$ 를 이용하여 나타내었고, 국소 화염 이동 속도에 의해 미소-면 요소가 변화하며 이동할 때, 미소 화염 면 요소의 넓이 변화(식 (1))를 조사하였다.

화염 스트레치를 화염 면의 형상과 화염 이동 속도 정보를 이용하여, 화염 면 국소 지점의 곡선 직교 좌표계를 이용하여, 아래와 같은 모델 식을 얻었다.

(9)

K = ({\vec{τ}}_{1} \circ \frac{\partial {\vec{v}}_{f, τ}}{\partial ξ_{1}} + {\vec{τ}}_{2} \circ \frac{\partial {\vec{v}}_{f, τ}}{\partial ξ_{2}}) + ({\vec{v}}_{f} \circ \vec{n}) ({\vec{τ}}_{1} \circ \frac{\partial \vec{n}}{\partial ξ_{1}} + {\vec{τ}}_{2} \circ \frac{\partial \vec{n}}{\partial ξ_{2}})

Fig. 1에 나타난 바와 같이, 위 식 (9)의 ${\vec{τ}}_{1}, {\vec{τ}}_{2}$ 는 국소 지점에서 화염 면에 접하는 단위 직교 접선 벡터들이며, $\vec{n}$ 는 화염 면에 수직인 단위 법선 벡터이다. ${\vec{v}}_{f}$ 는 국소 화염 이동 속도이며 ${\vec{v}}_{f, τ}$ 는 화염 면에 접하는 화염 이동 속도이다.

(10)

{\vec{v}}_{f} = {\vec{v}}_{f, n} + {\vec{v}}_{f, τ}

(11)

{\vec{v}}_{f, τ} = {\vec{v}}_{f} - ({\vec{v}}_{f} \circ \vec{n}) \vec{n}

S. H. Chung and C. K. Law는 (문헌에서 면-발산 연산자(surface divergence), $\nabla_{s} \circ$ 에 대한 규정을 하지 않았으나) 식 (12)와 같은 면-델 연산자(surface del operator) 전개 규칙을 적용하여 식 (13)과 같은 보다 간결한 형태의 화염 스트레치의 불변형(invariant form)의 모델 식으로 표현하였다.

(12)

\nabla_{s} = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}}

(13)

K = \nabla_{s} \circ {\vec{v}}_{f, τ} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})

S. H. Chung and C. K. Law의 유도와 모델 식의 특징은 화염 면 위에서의 정보만 사용하며 연산 또한 화염 면 위에서만 이루어진다. 화염 면에 이웃한 영역의 화염 면 밖에서의 정보와 연산을 요구하지 않는다. 그리고, 화염 면과 화염 이동 속도의 현시간 정보 외 현시간 전후의 정보를 요구하지 않는다. 따라서, 실험이나 수치해석의 데이터 분석을 위한 수학적 또는 수치적 적용 시 혼동이 적으며 비교적 간단하고 명료한 계산 수행이 가능하다.

2.1.3 Candel and Poinsot의 모델 식

M. Matalon[17]과 S. H. Chung and C. K. Law[18]는 미소 화염 면의 이동에 따른 넓이 변화를 조사하여 화염 스트레치 모델 식을 구하여 불변형(invariant form)으로 변형하였으나, S. M. Candel and T. J. Poinsot[19]은 플럭스 수송 정리(Flux Transport Theorem)를 이용하여 불변형의 형태로 유도하여 화염 스트레치 모델 식을 구하였다.

플럭스 수송 정리(Flux Transport Theorem)는 아래 Fig. 2와 같이, 3차원 벡터장(vector field) $\vec{ϕ} (\vec{r}, t)$ 내에서 2차원 면이 이동 속도 ${\vec{v}}_{f}$ 로 이동하며 변형할 때, 면을 지나는 플럭스(flux)의 총합의 시간 변화율을 나타낸다[25,26,27,28].

https://cdn.apub.kr/journalsite/sites/kosco/2023-028-02/N0590280203/images/ksssf_28_02_03_F2.jpg

Fig. 2.

A diagram of a moving surface in 3-dimensional space.

플럭스 수송 정리는 아래 식 (14), (15)와 같이 나타난다. 수식에 나타난 기호들을 Fig. 2에 나타내었다(문헌에 나타난 식들의 변수명, 연산식, 및 기호 표현들은 적절히 변경하였다.).

(14)

\frac{d Φ}{d t} = \frac{d}{d t} \iint_{A (t)}^{} \vec{ϕ} (\vec{r}, t) \circ d \vec{A}

(15)

\frac{d Φ}{d t} = \iint_{A (t)}^{} [\frac{\partial \vec{ϕ}}{\partial t} + (\nabla \circ \vec{ϕ}) {\vec{v}}_{f}] \circ d \vec{A} + \frac{d}{d t} \oint_{Γ (t)}^{} \vec{ϕ} \times {\vec{v}}_{f} \circ d \vec{r}

면 요소를 화염 면 요소 $δ A$ 로 설정하고 면의 이동 속도를 국소 화염 면 이동 속도 ${\vec{v}}_{f}$ 로 설정한다. 그리고, 벡터장 $\vec{ϕ} (\vec{r}, t)$ 를 국소 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 으로 설정하여 위 식 (14), (15)에 적용하고 전개하면 아래와 같은 관계식을 얻는다. (엄밀하게는, 단위 법선 벡터장 $\vec{n}$ 을 설정한다.)

(16)

\frac{1}{δ A} \frac{d (δ A)}{d t} = - (\vec{n} \circ \nabla) {\vec{v}}_{f} \circ \vec{n} + \nabla \circ {\vec{v}}_{f}

위 식 (16)의 좌변은 화염 스트레치의 정의(식 (1))이며, 우변의 첫 번째 항 $(\vec{n} \circ \nabla) {\vec{v}}_{f} \circ \vec{n}$ 을 아래 식 (17)의 정의를 이용하여 나타내어, 식 (19)의 화염 스트레치 모델 식을 얻었다(저자는 식 (17)의 연산 정의를 텐서(tensor) 표현식으로 식 (18)과 같이 정의하였다.).

(17)

\vec{n} \vec{n} : \nabla {\vec{v}}_{f} = (\vec{n} \circ \nabla) {\vec{v}}_{f} \circ \vec{n}

(18)

\vec{n} \vec{n} : \nabla {\vec{v}}_{f} = n_{j} \frac{\partial v_{f, i}}{\partial x_{j}} n_{i}

(19)

K = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f}

S. M. Candel and T. J. Poinsot의 유도와 모델 식의 특징은 수학적 정리(플럭스 수송 정리)를 이용하여 유도하므로, 화염 스트레치에 영향을 주는 인자들을 간과하는 오류를 최소화하였다.

그러나, Matalon의 모델 식(식 (6))의 경우와 유사하게, 연산을 위해 화염 면에 이웃한 영역의 화염 면 밖에서의 정보를 요구할 수 있다. 또한, Candel and Poinsot의 모델 식(식 (19))은 텐서 연산(식 (17) 또는 식 (18))을 요구하므로, Matalon과 Chung and Law의 모델 식들(식 (6), (13))에 비해 복잡한 계산이 요구된다(모델 식, 식 (19)의 적용에 관한 내용은 후에 자세히 논의한다.).

2.2 모델 식들의 비교

앞서 간략히 소개한 화염 스트레치 계산을 위한 3가지 모델 식들, i) Matalon(식 (6)), ii) Chung and Law(식 (13)), iii) Candel and Poinsot(식 (19)), 을 Table 1에 나타내었다. (Matalon의 모델 식, 식 (6)의 화염 면 위에서의 정보를 의미하는 ${\{\}}_{F = 0}$ 기호는 생략하고 추가 정보에 포함하였다.)

Table 1.

Flame stretch model equations

Author	Flame stretch model equation	Additional information	Ref.
M. Matalon	$K = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} - \frac{\partial F / \partial t}{\| \nabla F \|} (\nabla \circ \vec{n})$	$F = 0, \frac{\partial F / \partial t}{\| \nabla F \|} = - {\vec{v}}_{f} \circ \vec{n}$	[17]
S. H. Chung and C. K. Law	$K = \nabla_{s} \circ {\vec{v}}_{f, τ} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$	${\vec{v}}_{f, τ} = {\vec{v}}_{f} - ({\vec{v}}_{f} \circ \vec{n}) \vec{n}$	[18]
S. M. Candel and T. J. Poinsot	$K = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f}$	$\vec{n} \vec{n} : \nabla {\vec{v}}_{f} = n_{j} \frac{\partial v_{f, i}}{\partial x_{j}} n_{i}$	[19]

3 모델 식들은 서로 다른 형태를 가지고 있으며, 요구하는 연산이 각각 다르지만, 같은 화염 스트레치를 나타낸다. 3 모델 식들의 동일함을 아래 묘사하였다.

2.2.1 Matalon 모델 식과 Chung and Law 모델 식의 비교

Matalon 모델 식, 식 (6)와 Chung and Law 모델 식, 식 (13)을 비교하기 위해, 먼저, 각 수식의 첫 번째 항을 비교해보았다. Table 1의 Matalon 모델 식의 첫 번째 항 $- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n}$ 과 Chung and Law 모델 식의 첫 번째 항 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 과 비교해 보면 서로 다른 형태를 가지고 있다.

Matalon 모델 식의 첫 번째 항 $- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n}$ 에, 위 식 (10)을 적용하여, 화염 이동 속도 ${\vec{v}}_{f}$ 를 국소 화염 면에 수직인 성분 ${\vec{v}}_{f, n}$ 과 접하는 성분 ${\vec{v}}_{f, τ}$ 의 합으로 나타내면 ${\vec{v}}_{f, n} \times \vec{n} = 0$ 이므로, 국소 화염 면에 평행한 성분 ${\vec{v}}_{f, τ}$ 와 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 의 연산으로 아래와 같이 나타낼 수 있다.

(20)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} = - \nabla \times ({\vec{v}}_{f, τ} \times \vec{n}) \circ \vec{n}

벡터 항등식(vector identity)를 이용하여 위 식 (20)의 우변을 전개하면 아래와 같다.

(21)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} = - {\vec{v}}_{f, τ} (\nabla \circ \vec{n}) \circ \vec{n} + \vec{n} (\nabla \circ {\vec{v}}_{f, τ}) \circ \vec{n} - (\vec{n} \circ \nabla) {\vec{v}}_{f, τ} \circ \vec{n} + ({\vec{v}}_{f, τ} \circ \nabla) \vec{n} \circ \vec{n}

위 식 (21)의 우변의 첫 번째 항 $- {\vec{v}}_{f, τ} (\nabla \circ \vec{n}) \circ \vec{n}$ 는 ${\vec{v}}_{f, τ}$ 와 $\vec{n}$ 은 직교하므로 0이며, 두 번째 항 $\vec{n} (\nabla \circ {\vec{v}}_{f, τ}) \circ \vec{n}$ 은 $\vec{n} \circ \vec{n} = 1$ 이므로 $\nabla \circ {\vec{v}}_{f, τ}$ 이다. 세 번째 항 $- (\vec{n} \circ \nabla) {\vec{v}}_{f, τ} \circ \vec{n}$ 을 조사하기 위해 벡터 항등식을 이용하여 아래와 같이 전개하였다.

(22)

- (\vec{n} \circ \nabla) {\vec{v}}_{f, τ} \circ \vec{n} = \vec{n} \circ \nabla ({\vec{v}}_{f, τ} \circ \vec{n}) - (\vec{n} \circ \nabla \vec{n}) \circ {\vec{v}}_{f, τ}

위 식 (22)에서, ${\vec{v}}_{f, τ}$ 와 $\vec{n}$ 은 직교하므로 $\vec{n} \circ \nabla ({\vec{v}}_{f, τ} \circ \vec{n}) = 0$ 이다. $- (\vec{n} \circ \nabla \vec{n}) \circ {\vec{v}}_{f, τ}$ 항은 벡터 항등식을 이용하여 아래 식 (23)과 같이 전개할 수 있다.

(23)

- (\vec{n} \circ \nabla) \circ {\vec{v}}_{f, τ} = - \frac{1}{2} \nabla (\vec{n} \circ \vec{n}) \circ {\vec{v}}_{f, τ} + \vec{n} \times (\nabla \times \vec{n}) \circ {\vec{v}}_{f, τ}

$\vec{n} \circ \vec{n} = 1$ 과 $\nabla \times \vec{n} = 0$ 을 이용하면 위 식 (23), $- (\vec{n} \circ \nabla) \circ {\vec{v}}_{f, τ} = 0$ 임을 알 수 있으며, 식 (22), (23)으로부터, 위 식 (21)의 세 번째 항 $- (\vec{n} \circ \nabla) {\vec{v}}_{f, τ} \circ \vec{n}$ 은 0이다.

위 식 (21)의 우변의 네 번째 항 $({\vec{v}}_{f, τ} \circ \nabla) \vec{n} \circ \vec{n}$ 은 $\vec{n} \circ \vec{n} = 1$ 이므로 0이다.

각 항의 결과를 식 (21)에 적용하면, Table 1의 Matalon 모델 식의 첫 번째 항은 아래와 같이 나타난다.

(24)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} = \nabla \circ {\vec{v}}_{f, τ}

즉, 위 식 (24), Matalon 모델 식과 Table 1의 Chung and Law 모델 식의 첫 번째 항을 비교해 보면 $\nabla \circ {\vec{v}}_{f, τ}$ 과 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 의 차이가 있다.

$\nabla \circ {\vec{v}}_{f, τ}$ 을 국소 미소-면에 접하는 곡선 좌표계에서 나타내면 식 (25)와 같다. 곡선 좌표계에서 면-델 연산자(surface del operator)의 정의, 식 (12),를 적용하면 식 (26)과 같이 $\nabla \circ {\vec{v}}_{f, τ}$ 과 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 의 관계식을 얻을 수 있다.

(25)

\nabla \circ {\vec{v}}_{f, τ} = (\vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}} + \vec{n} \frac{\partial}{\partial η}) \circ {\vec{v}}_{f, τ}

(26)

\nabla \circ {\vec{v}}_{f, τ} = \nabla_{s} \circ {\vec{v}}_{f, τ} + \vec{n} \circ \frac{\partial}{\partial η} {\vec{v}}_{f, τ}

위 식 (26)의 우변의 두 번째 항 $\vec{n} \circ \frac{\partial}{\partial η} {\vec{v}}_{f, τ}$ 은 0이므로 $\nabla \circ {\vec{v}}_{f, τ}$ 과 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 은 동일함을 알 수 있다.

(27)

\nabla \circ {\vec{v}}_{f, τ} = \nabla_{s} \circ {\vec{v}}_{f, τ}

따라서, Table 1의 Matalon 모델 식의 첫 번째 항 $- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n}$ 과 Chung and Law 모델 식의 첫 번째 항 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 은 동일하다.

(28)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} = \nabla_{s} \circ {\vec{v}}_{f, τ}

다음으로, 각 수식의 두 번째 항을 비교해보았다. Table 1의 Matalon 모델 식의 두 번째 항 $\frac{- \partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n})$ 을 추가 정보(식 (8))을 이용하여 나타내면 $({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n})$ 으로 나타나며, Chung and Law 모델 식의 두 번째 항 $({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 과 비교해보면 $\nabla \circ \vec{n}$ 과 $\nabla_{s} \circ \vec{n}$ 의 차이가 있다.

$\nabla \circ \vec{n}$ 을 국소 미소-면에 접하는 곡선 좌표계에서 나타내면 아래 식 (29)와 같으며, 곡선 좌표계에서 면-델 연산자(surface del operator)의 정의를 적용하면 아래 식 (30)과 같이 $\nabla \circ \vec{n}$ 과 $\nabla_{s} \circ \vec{n}$ 의 관계식을 얻을 수 있다.

(29)

\nabla \circ \vec{n} = (\vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}} + \vec{n} \frac{\partial}{\partial η}) \circ \vec{n}

(30)

\nabla \circ \vec{n} = \nabla_{s} \circ \vec{n} + \vec{n} \circ \frac{\partial}{\partial η} \vec{n}

위 식 (29), (30)에서, $\vec{τ_{1}}, \vec{τ_{2}}, \vec{n}$ 은 서로 직교하나 $\vec{τ_{1}} \circ \frac{\partial \vec{n}}{\partial ξ_{1}}$ 과 $\vec{τ_{2}} \circ \frac{\partial \vec{n}}{\partial ξ_{2}}$ 은 0을 의미하지 않으며, 곡면 위를 따라 방향이 변화하는 국소 면에 수직한 단위 법선 벡터 $\vec{n}$ 의 $\vec{τ_{1}}, \vec{τ_{2}}$ 방향의 변화율을 의미한다 따라서, $\nabla_{s} \circ \vec{n}$ 은 0이 아니다. 또한 식 (30)의 우변의 두 번째 항 $\vec{n} \circ \frac{\partial}{\partial η} \vec{n}$ 은 0이므로 $\nabla \circ \vec{n}$ 과 $\nabla_{s} \circ \vec{n}$ 은 동일함을 알 수 있다.

(31)

\nabla \circ \vec{n} = \nabla_{s} \circ \vec{n}

(여기서, $\nabla_{s} \circ \vec{n}$ 는 곡률(curvature)이며 이의 적용과 계산에 관한 내용은 “화염 면의 곡률 산출” 부분에서 자세히 논의한다.)

따라서, Table 1의 Matalon 모델 식의 두 번째 항 $\frac{- \partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n})$ 과 Chung and Law 모델 식의 두 번째 항 $({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 은 동일하다.

(32)

\frac{- \partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n}) = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})

위 식 (28), (32)로부터, Matalon 모델 식, 식 (6)과 Chung and Law 모델 식, 식 (13)은 동일하다(Table 1 참조).

(33)

K = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} - \frac{\partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n}) = \nabla_{s} \circ {\vec{v}}_{f, τ} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})

2.2.2 Matalon 모델 식과 Candel and Poinsot 모델 식의 비교

Candel and Poinsot의 모델 식(식 (19))은 Matalon(식 (6))과 Chung and Law(식 (13))의 모델 식들과 매우 다른 형태를 가지고 있으며 각 항의 대응 여부도 쉽게 파악되지 않는다(Table 1 참조). Matalon의 모델 식(식 (6))과 Candel and Poinsot의 모델 식(식 (19))을 비교하여 동일함을 묘사하였다.

Table 1의 Matalon 모델 식에 추가 정보(식 (8))를 적용하면 아래와 같이 나타난다.

(34)

K = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n})

위 식 (34)의 우변을 벡터 항등식을 이용하여 전개하면 다음과 같다.

(35)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n}) = - {\vec{v}}_{f} (\nabla \circ \vec{n}) \circ \vec{n} + \vec{n} (\nabla \circ {\vec{v}}_{f}) \circ \vec{n} - (\vec{n} \circ \nabla) {\vec{v}}_{f} \circ \vec{n} + ({\vec{v}}_{f} \circ \nabla) \vec{n} \circ \vec{n} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n})

위 식 (35)에서 우변의 첫 번째 항과 마지막항을 상쇄하고, $\vec{n} \circ \vec{n} = 1$ 을 이용하면 아래 수식과 같이 나타난다.

(36)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n}) = - (\vec{n} \circ \nabla) {\vec{v}}_{f} \circ \vec{n} + \nabla \circ {\vec{v}}_{f}

앞서 언급한 텐서 연산 기호의 정의, 식 (17), 을 적용하면 다음과 같다.

(37)

- \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} + ({\vec{v}}_{f} \circ \vec{n}) (\nabla \circ \vec{n}) = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f}

위 식 (37)로부터, Matalon 모델 식, 식 (6)과 Candel and Poinsot의 모델 식, 식 (19)는 동일하다(Table 1 참조).

(38)

K = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n} - \frac{\partial F / \partial t}{| \nabla F |} (\nabla \circ \vec{n}) = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f}

위 식 (33), (38)로부터, Matalon 모델 식과 Chung and Law 모델 식은 동일하며, Matalon 모델 식과 Candel and Poinsot의 모델 식은 동일하므로, 화염 스트레치 계산을 위한 3가지 모델 식들, i) Matalon(식 (6)), ii) Chung and Law(식 (13)), iii) Candel and Poinsot(식 (19)), 은 모두 동일함을 알 수 있다.

3. 화염 스트레치의 분해 표현식

화염 스트레치 모델 식들은 화염의 거동에 따른 분류를 이용하거나, 화염의 이동에 기여하는 인자들의 분류를 이용하여 분해한 형태로 표현할 수 있다.

3.1 화염 거동에 따른 스트레치 분해 표현 식

화염 스트레치 모델 식들을 화염의 거동을 고려하여 분해한 형태로 표현할 수 있다. 예를 들어, Chung and Law의 모델 식(식 (13), 또는 Table 1)은 2개의 항으로 이루어져 있다. 첫 번째 항 $\nabla_{s} \circ {\vec{v}}_{f, τ}$ 은 화염 면에 평행한 화염 이동 속도 성분의 면-발산(surface divergence)이며, 화염 면이 화염 면에 접하는 방향으로 이동하며(곡률은 유지한 상태로) 발생하는 넓이의 시간 변화율을 의미한다. 두 번째 항 $({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$ 은 화염 면에 수직한 법선 화염 이동 속도 성분과 곡률( $\nabla_{s} \circ \vec{n}$ )의 곱이며, 화염 면이 화염 면의 수직 방향으로 이동하며(곡률의 변화와 함께) 발생하는 넓이의 시간 변화율을 의미한다.

이러한 화염 스트레치의 두 항을 각각 접선 화염 스트레치(tangential stretch) $K_{τ}$ 와 법선 화염 스트레치(normal stretch) $K_{n}$ 으로 정의하면, 화염 스트레치 $K$ 는 법선과 접선 화염 스트레치 , $K_{τ}$ 의 합으로 아래 식 (39)와 같이 나타낼 수 있다. 예를 들어, Chung and Law의 모델 식(식 (13), 또는 Table 1)의 경우 법선 화염 스트레치 $K_{n}$ 접선 화염 스트레치 $K_{τ}$ 은 아래와 식 (40), (41)과 같이 나타낼 수 있다.

(39)

K = K_{τ} + K_{n}

(40)

K_{τ} = \nabla_{s} \circ {\vec{v}}_{f, τ}

(41)

K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n})

화염 스트레치 계산을 위한 3가지 모델 식들의 각각 화염 거동에 따른 법선 화염 스트레치 $K_{n}$ 과 접선 화염 스트레치 $K_{τ}$ 의 표현 식들을 Table 2에 나타내었다(Candel and Poinsot의 모델 식은, 다른 2 모델 식들과는 달리, 문헌의 화염 스트레치 모델 식이 법선과 접선 스트레치의 형태가 자명하게 표현되어 있지 않아 적절히 변형하였다.).

Table 2.

Flame stretch expressions in terms of tangential and normal stretches

Author	Flame stretch $K (= K_{τ} + K_{n})$
Author	Tangential stretch $K_{τ}$	Normal stretch $K_{n}$
M. Matalon	$K_{τ} = - \nabla \times ({\vec{v}}_{f} \times \vec{n}) \circ \vec{n}$	$K_{n} = - \frac{\partial F / \partial t}{\| \nabla F \|} (\nabla \circ \vec{n}) (or, K_{n} = - \frac{\partial F / \partial t}{\| \nabla F \|} κ)$
S. H. Chung and C. K. Law	$K_{τ} = \nabla_{s} \circ {\vec{v}}_{f, τ}$	$K_{n} = ({\vec{v}}_{f} \circ \vec{n}) (\nabla_{s} \circ \vec{n}) (or, K_{n} = ({\vec{v}}_{f} \circ \vec{n}) κ)$
S. M. Candel and T. J. Poinsot	$K_{τ} = \nabla \circ {\vec{v}}_{f, τ}$	$K_{n} = - \vec{n} \vec{n} : \nabla {\vec{v}}_{f} + \nabla \circ {\vec{v}}_{f, n}$

• $K = K_{τ} + K_{n} κ = \nabla_{s} \circ \vec{n} (or \nabla \circ \vec{n}) {\vec{v}}_{f, τ} = {\vec{v}}_{f} - ({\vec{v}}_{f} \circ \vec{n}) \vec{n} \frac{\partial F / \partial t}{| \nabla F |} = - {\vec{v}}_{f} \circ \vec{n}$

Table 2를 살펴보면, 접선 화염 스트레치 $K_{τ}$ 는 화염 면에 접하는 화염 이동 속도의 화염 면에 따른 공간 변화( $\nabla_{s} \circ {\vec{v}}_{f, τ}$ )에 직접적으로 기인하며, 법선 화염 스트레치 $K_{n}$ 는 화염 면의 곡률( $\nabla_{s} \circ \vec{n}$ )과 화염 면에 수직한 이동 속도 성분( ${\vec{v}}_{f} \circ \vec{n}$ )에 직접적으로 기인한다. 정상 상태의 화염 면의 경우, 화염 면의 형상이 시간에 따라 변화하지 않으므로, 국소 지점에서 화염 면이 화염 면의 수직한 방향으로 이동하지 않는다( ${\vec{v}}_{f} \circ \vec{n} = 0$ ). 따라서, 법선 화염 스트레치 $K_{n}$ 은 0이다. 즉, 곡률에 의한 법선 화염 스트레치는 0이다. 그러나, ( $K_{τ}$ 와 $K_{n}$ 의 총합인) 화염 스트레치 $K$ 에 대한 곡률에 의한 효과는 간접적으로 존재하며, 접선 스트레치 $K_{τ}$ 에 곡률의 효과가 내재적으로 포함되어있다. 접선 스트레치 $K_{τ}$ 는 화염 면에 평행한 이동 속도의 화염 면을 따르는 공간 변화율이며, 화염 면의 방향이 곡률과 함께 변화되는 효과가 포함되므로, 곡률의 효과가 작용하며, 곡률에 의한 효과는 내재적으로 존재한다.

3.2 유동 속도와 화염 전파 속력에 따른 스트레치 분해 표현 식

다른 표현 방법으로, 화염 스트레치 모델 식들을 화염의 이동에 기여하는 인자들을 고려하여 분해한 형태로 표현할 수 있다.

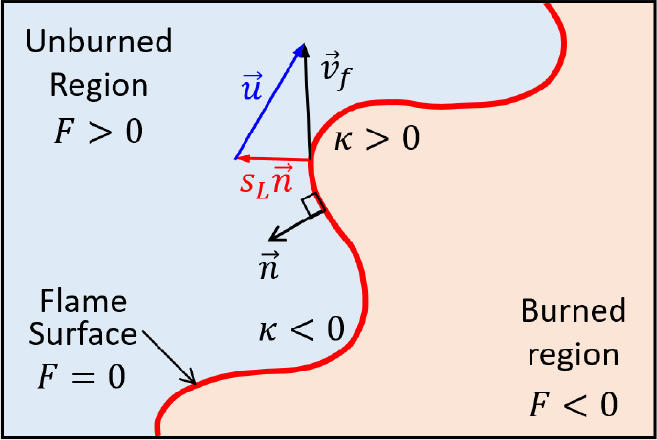
화염은 유동에 의해 이동됨과 동시에 연소 현상에 의해 화염 면에 수직 방향으로 비반응 영역(unburned region)을 향해 전파한다[29]. 국소 지점에서 화염 이동 속도 ${\vec{v}}_{f}$ 는 유동 속도 $\vec{u}$ , 화염 전파 속력 $s_{L}$ , 그리고 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 으로 아래 식 (42)과 같이 나타낼 수 있다[29].

(42)

{\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}

위 식 (42)에서는 화염 면에 수직인 단위 법선 벡터 $\vec{n}$ 을 화염 면 위에서 비반응 영역(unburned region)을 향해 정의하여 화염이 연소에 의해 전파하는 방향과 수직한 단위 법선 벡터 $\vec{n}$ 의 방향을 일치하도록 하였다(만약, 반응 완료 영역(burned region)을 향해 $\vec{n}$ 의 방향을 정의한다면 식 (42)의 두 번째 항의 부호를 음으로 변경하여야 한다. (Table 4 참조)).

화염 스트레치 모델 식들에 위 식 (42)를 적용하여 유동 속도에 의한 스트레치와 연소 현상에 따른 화염 전파 속력에 의한 스트레치 성분으로 분해한 형태로 표현할 수 있다. 예를 들어, Chung and Law의 모델 식(식 (13), 또는 Table 1)에 위 식 (42)를 적용하면 아래와 같다.

(43)

K = \nabla_{s} \circ {\vec{u}}_{τ} + (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n}) + s_{L} (\nabla_{s} \circ \vec{n})

첫 번째와 두 번째 항은 화염이 유동 속도 $\vec{u}$ 에 의해 이동됨에 따른 화염 스트레치 성분이며, 세 번째 항은 화염이 연소와 함께 전파 속력 $s_{L}$ 로 전파됨에 따른 화염 스트레치 성분이다.

유동의 불균일성에 의한 화염 스트레치에 관련한 첫 번째와 두 번째 항의 합을 스트레치 $K_{u}$ 라 정의한다(문헌에 따라 변형률(strain)이라 명명하기도 한다.). 화염이 연소에 의해 화염 면에 수직 방향으로 전파함에 따른 화염 스트레치에 관련한 세 번째 항을 스트레치 $K_{s_{L}}$ 라 정의한다. 화염 스트레치 $K$ 는 유동과 화염 전파에 기인한 스트레치 $K_{u}$ 와 $K_{s_{L}}$ 의 합으로 아래 식 (44)와 같이 나타낼 수 있다. 예를 들어, Chung and Law의 모델 식(식 (13), 또는 Table 1)의 경우 유동에 의한 화염 스트레치 $K_{u}$ 와 화염 전파에 의한 스트레치 $K_{s_{L}}$ 은 아래와 식 (45), (46)과 같이 나타낼 수 있다.

(44)

K = K_{u} + K_{s_{L}}

(45)

K_{u} = \nabla_{s} \circ {\vec{u}}_{τ} + (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n})

(46)

K_{s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})

화염 스트레치 계산을 위한 3가지 모델 식들을 유동에 의한 이동과 화염의 연소에 의한 전파의 요인에 기인한 스트레치 $K_{u}$ 와 $K_{s_{L}}$ 로 분류하여 표현한 식들을 Table 3에 나타내었다.

Table 3.

Flame stretch expressions in terms of flow velocity and flame propagation velocity

Author	Flame stretch $K (= K_{u} + K_{s_{L}} = K_{τ, u} + K_{n, u} + K_{s_{L}})$
	Strain (Stretch by flow velocity) $K_{u} (= K_{τ, u} + K_{n, u})$		Stretch by flame propagation $K_{s_{L}}$
	Tangential stretch by flow velocity $K_{τ, u}$	Normal stretch by flow velocity $K_{n, u}$	Normal stretch by flame propagation $K_{n, s_{L}} (= K_{s_{L}})$
M. Matalon	$K_{u} = - \nabla \times (\vec{u} \times \vec{n}) \circ \vec{n} + (\vec{u} \circ \vec{n}) (\nabla \circ \vec{n})$		$K_{s_{L}} = s_{L} (\nabla \circ \vec{n})$
	$K_{τ, u} = - \nabla \times (\vec{u} \times \vec{n}) \circ \vec{n}$	$K_{n, u} = (\vec{u} \circ \vec{n}) (\nabla \circ \vec{n})$	$K_{n, s_{L}} = s_{L} (\nabla \circ \vec{n})$
S. H. Chung and C. K. Law	$K_{u} = \nabla_{s} \circ {\vec{u}}_{τ} + (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$		$K_{s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
	$K_{τ, u} = \nabla_{s} \circ {\vec{u}}_{τ}$	$K_{n, u} = (\vec{u} \circ \vec{n}) (\nabla_{s} \circ \vec{n})$	$K_{n, s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
S. M. Candel and T. J. Poinsot	$K_{u} = - \vec{n} \vec{n} : \nabla \vec{u} + \nabla \circ \vec{u}$		$K_{s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$
	$K_{τ, u} = \nabla \circ {\vec{u}}_{τ}$	$K_{n, u} = - \vec{n} \vec{n} : \nabla \vec{u} + \nabla \circ {\vec{u}}_{n}$	$K_{n, s_{L}} = s_{L} (\nabla_{s} \circ \vec{n})$

• For Matalon’s model equation, $\frac{\partial F / \partial t}{| \nabla F |} = - {\vec{v}}_{f} \circ \vec{n}$ is applied.

• ${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$

• $K = K_{u} + K_{s_{L}} K_{u} = K_{τ, u} + K_{n, u} K_{s_{L}} = K_{n, s_{L}} κ = \nabla_{s} \circ \vec{n} (or \nabla \circ \vec{n})$

또한, 유동 속도에 의한 화염 스트레치 $K_{u}$ 의 경우, 앞서 언급한 접선 화염 스트레치 $K_{τ}$ 와 법선 화염 스트레치 $K_{n}$ 에 기여하는 성분으로 다시 분류할 수 있으며 이를 각각 $K_{τ, u}, K_{n, u}$ 으로 명명하여 표기하였다.

(47)

K_{u} = K_{τ, u} + K_{n, u}

화염 전파 속력에 의한 스트레치 $K_{s_{L}}$ 의 경우, 화염은 연소 현상에 의해 화염 면에 수직 방향으로만 전파하므로 접선 화염 스트레치 $K_{τ}$ 에 기여하지 않으며, 오직 법선 화염 스트레치 $K_{n}$ 에 기여한다( $K_{n, s_{L}} = K_{s_{L}}$ , Table 3 참조).

3가지 모델 식들을 유동 속도에 의한 접선, 법선 화염 스트레치 $K_{τ, u}, K_{n, u}$ 와 화염 전파 속력에 의한 (법선) 화염 스트레치 $K_{s_{L}}$ 로 분류한 표현 식들도 Table 3에 나타내었다(Candel and Poinsot의 모델 식은, 다른 2 모델 식들과는 달리, 문헌의 모델 식이 법선과 접선 스트레치의 형태가 자명하게 표현되어 있지 않아 적절히 변형하였다.).

4. 화염 스트레치 모델 식 적용의 이론적, 수치적, 실험적 접근의 비교

앞서 언급한 바와 같이 화염 스트레치 모델 식들은 유도과정과 배경이 다소 차이가 있으며, 이에 따라 이론적 연구를 위한 모델 전개 목적이나 수치해석 및 실험 데이터를 분석하여 화염 스트레치를 산출하려는 목적에 따라 운용과 전개가 달라지게 된다. 모델 식들의 이론적, 수치적, 실험적 접근을 위한 응용의 특이점과 장단점들을 모델 식 유도의 수학적 배경과 함께 고찰하였다.

4.1 화염 면의 정의

화염 면의 정의는, 이론적 전개, 수치해석 수행 및 데이터 분석, 실험 데이터의 분석 등, 목적에 따라 다소 달라질 수 있다.

이론적 전개를 목적으로 사용될 때 자주 사용되는 방법으로, 화염 면을 정의하기 위하여 아래 식 (48)을 이용한다.

(48)

F (x, y, z, t) = C

$C$ <0 : in burned region

$C$ =0 : on flame surface

$C$ >0 : in unburned region

위 식 (48)에서 3차원 공간에서 화염 면을 정의하기 위하여 스칼라 장 $F (x, y, z, t)$ 을 정의한다. 우변 항의 상수 $C$ 에 따라, $C$ >0이면 비반응 영역(unburned region)을, $C$ <0이면 반응 완료 영역(burned region)을 나타낸다. 특히, $C$ =0일 경우 화염 면을 나타내며 앞서 언급한 식 (2)와 동일하다(본 문서에서는 상수 $C$ 에 따른 영역 구분 및 화염 면 지칭을 위해 Table 4의 Fig. (a)를 따른다. 또한, 스칼라 장 $F (x, y, z, t)$ 는 화염 면의 형상 정보를 담고 있으며, 본 문서에서는 편의상 $F (x, y, z, t)$ 를 화염 형상 함수라 부른다.).

Table 4.

Surface unit normal vector definition and corresponding curvature, flame shape scalar function, and flame propagation velocity

Surface unit normal vector $\vec{n}$	Flame shape scalar function $F (\nabla F = \| \nabla F \| \vec{n})$	Flame movement velocity ${\vec{v}}_{f}$	Curvature $κ (= \nabla_{s} \circ \vec{n})$
Toward unburned region	Unburned region: $F$ >0 Flame surface: $F$ =0 Burned region: $F$ <0	${\vec{v}}_{f} = \vec{u} + s_{L} \vec{n}$	Convex toward unburned region: $κ > 0$ Concave toward unburned region: $κ < 0$
(a) Surface normal vector, flame shape function, flame movement velocity		(b) Curvature and radius of curvature

이러한 스칼라 장 $F (x, y, z, t)$ 은 화염 면을 근사하기 위해 사용되는 특성치 변수(온도, 화학종, 등)의 스칼라 장과는 구분되어야 한다. 예를 들어, 화염 면을 근사하기 위해 온도의 등고면(등온면)을 자주 사용하게 된다. 이 경우, 전 영역에서 온도의 스칼라 장이 존재하나, 화염 면 형상 함수 $F (x, y, z, t)$ 스칼라 장을 전 영역과 시간에서 근사할 수 없다(화염 면 형상 함수 $F (x, y, z, t)$ 스칼라 장의 경우, 화염 면 주위의 앞/뒤에 화염 면 이동 속도 장이 존재하며 연속적이다. 그에 반해, 화염 면 근사를 위해 사용된 온도의 스칼라 장의 경우에는 화염 면 앞/뒤에서 화염 면 이동 속도 장이 정의되지 않으며 유동 장 규모(length scale)로 관측하면 유동 장 변수들이 불연속하다.).

이론적 전개를 위한 화염 면의 정의에서 주목할 점은, 화염 형상 함수 $F (x, y, z, t)$ 와 화염 면의 정의(식 (48))가 전체 공간과 시간에 대해 스칼라 장(scalar field)으로 존재한다는 것이다. 또한, 이에 연관된 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ , 화염 이동 속도 ${\vec{v}}_{f}$ 도 전체 공간과 시간에 대해 벡터장(vector field)으로 존재한다.

이에 반해, 수치해석이나 실험 데이터 분석 목적의 경우에 사용되는 화염 면의 정의를 엄밀하게 표현하면 아래와 같다.

(49)

\{(x, y, z) | F (x, y, z, t) = 0, t = t_{n}\}

즉, 화염 면 정의의 조건을 만족하는, 현재 시간에서의 등고면 위치 정보의 집합으로 화염 면을 정의하게 된다. 이 경우, 오직 화염 면 위에서의 정보들(화염 면의 위치 $(x, y, z)$ , 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ , 그리고 화염 이동 속도 ${\vec{v}}_{f}$ , 등)만 주어지며, 화염 면 밖에서의 정보는 존재하지 않는다(또한, 화염 형상 함수 $F (x, y, z, t)$ 도 정의되지 않는다. 화염 면의 위치 정보만이 주어지며, 화염 면 위의 정보를 만족하는 화염 형상 함수 $F (x, y, z, t)$ 를 구한 경우에도, 식 (48)의 $C$ ≠0의 조건의 가 정의 $F (x, y, z, t)$ 되지 않는다.).

이러한 차이들이 이론적 접근과 수치해석 및 실험적 접근 시 화염 스트레치 계산에 영향을 주게 된다. 앞서 언급하였듯이, 이론적 전개를 바탕으로 유도된 Matalon의 모델 식(식 (6), 또는 Table 1)의 경우 델 연산자( $\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}$ )를 이용한 기울기-벡터(gradient) 연산, 발산(divergence) 연산, 및 벡터장-회전(curl) 연산을 위하여 화염 면 밖에서의 정보들을 요구하며, 화염 형상 함수의 시간 미분( $\frac{\partial}{\partial t}$ )을 위하여 현재 시간 외의 화염 형상 함수의 정보를 요구한다. Candel and Poinsot의 모델 식(식 (19), 또는 Table 1)의 경우에도, 발산 연산을 위해 화염 면 밖에서의 정보들을 요구하며, 복잡한 텐서 연산을 수행해야 한다.

이러한 모델 식들을 수치해석 및 실험적 접근에 적용하여 화염 스트레치를 산출할 경우, 식 (49)와 같이 화염 면의 정보가 오직 현재 시간에서의 화염 면 위에서만 주어지기 때문에, 바로 적용할 수 없다.

한편, 화염 면의 형상만을 고려하여 유도된 Chung and Law의 모델 식(식 (13), Table 1)의 경우에는, 면-발산(surface-divergence) 연산을 통해 화염 면 위의 정보만을 요구하며, 현재 시간 외 화염의 정보를 요구하지 않는다. 따라서, 수치해석 및 실험적 접근에 적용하여 화염 스트레치를 산출할 경우, 식 (49)의 정보만으로 쉽게 적용할 수 있다.

4.2 화염 면 단위 법선 벡터 설정 및 적용

화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 의 설정과 계산은 앞서 설명한 화염 면의 정의 방법에 따라 달라질 수 있다.

이론적 전개를 목적으로 사용될 때, 화염 면의 정의가 식 (48)과 같이 되었을 때, 면에 수직한 단위 법선 벡터장 $\vec{n} (x, y, z, t)$ 으로 존재하게 된다. 화염 면 단위 법선 벡터 $\vec{n}$ 은 화염 면 뿐만 아니라 전 영역에 대해 존재하며 현재 시간 외의 시간 영역에서도 존재하게 된다.

화염 면 단위 법선 벡터 $\vec{n}$ 은 화염 형상 함수 $F (x, y, z, t)$ 와 아래 식 (50)과 같은 관계식을 만족한다. 화염 형상 함수 $F$ 와 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 이 전체 공간과 시간에 대해 존재하므로, 아래 식 (50)의 델 연산자(𝛻)를 수행할 수 있다. 이론적 전개를 바탕으로 유도된 Matalon과 Candel and Poinsot의 모델 식들(식 (6), (19) 또는 Table 1)이 아래 식 (50)의 정의를 사용한다.

(50)

\vec{n} = \frac{\nabla F}{|\nabla F|}

(본 문서의 화염 형상 함수 $F$ 의 정의 규칙을 따르면 화염 면 단위 법선 벡터 $\vec{n}$ 은 비반응 영역을 향하게 된다. Table 4의 Fig. (a) 참조).

이에 반해, 수치해석이나 실험 데이터 분석의 목적의 경우, 식 (49)와 같이 화염 면의 위치와 화염 면 위에서의 정보만 주어지므로, 위 식 (50)을 사용할 수 없으며, 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 은 화염 면의 형상만을 고려하여 설정하여야 한다. 3차원 공간 내 화염일 경우, 화염 면 위에서 화염 면에 접하는 단위 직교 접선 벡터들 $\vec{τ_{1}}, \vec{τ_{2}}$ 을 구하여, 오른손 법칙의 벡터 외적(cross product)을 이용하여 $\vec{n}$ 을 구한다. 2차원 공간 내 화염일 경우 화염 면 위의 단위 접선 벡터를 구하여, 이에 수직하도록 $\vec{n}$ 을 구한다. Chung and Law의 모델 식(식 (13), Table 1)을 사용할 경우, 아래 식 (51)의 정의를 사용하여 단위 법선 벡터 $\vec{n}$ 을 설정할 수 있다.

(51)

\vec{n} = {\vec{τ}}_{1} \times {\vec{τ}}_{2} {\vec{τ}}_{1} ⊥ {\vec{τ}}_{2}, | {\vec{τ}}_{1} | = | {\vec{τ}}_{2} | = 1

화염 면의 위치 정보만으로 화염 면 단위 법선 벡터 $\vec{n}$ 을 구하기 때문에 $\vec{n}$ 의 방향은 2가지 선택(반응 완료 영역과 비반응 영역 방향)이 가능하다. 그러나, 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 과 곡률 𝜅, 화염 이동 속도 ${\vec{v}}_{f}$ , 그리고 화염 전파 속력 $s_{L}$ 의 정의는 서로 연관되어 있으며, 상호 정확한 호환이 되도록 설정되어야 한다. 식 (51)을 사용할 경우, 본 문서에서 설정한 규칙(Table 4의 Fig. (a))을 따라, $\vec{n}$ 이 비반응 영역을 향하도록 인위적으로 설정한다.

4.3 화염 면의 곡률 산출

화염 면의 곡률 𝜅는 화염 면 위의 화염 면에 수직한 단위 법선 벡터 $\vec{n}$ 의 면-발산으로 아래 식 (52)와 같이 나타난다.

(52)

κ = \nabla_{s} \circ \vec{n}

화염 면 곡률의 정의는, 화염 면 단위 법선 벡터 $\vec{n}$ 의 화염 면에 따른 (방향) 변화를 통해, 화염 면의 구부러짐 정도를 나타낸다. 화염 면에 따른 변화를 계산하기에 면-발산(surface divergence) 연산을 사용하며 면-델 연산자( $\nabla_{s}$ )를 사용한다.

화염 면의 곡률 𝜅는 화염 스트레치 모델 식에 명시적으로 나타나거나 다른 항에 암묵적으로 포함되어있다. Table 1, 2, 3에 𝜅 또는 $\nabla_{s} \circ \vec{n}$ 으로 표현되어 있다.

Matalon과 Candel and Poinsot의 모델 식들(식 (6), (19) 또는 Table 1)은 곡률 𝜅를 $\nabla \circ \vec{n}$ 의 표현식으로 사용한다. 이론적 전개의 경우, 화염 면 단위 법선 벡터 $\vec{n}$ 이 벡터장 $\vec{n} (x, y, z, t)$ 으로 존재하며, 화염 면 뿐만 아니라 전 영역에 존재하므로, 화염 면 위의 정보 뿐만 아니라 화염 면 밖의 정보를 요구하는, 일반 델 연산자(𝛻)를 이용한 발산 연산(divergence)이 가능하다.

그러나, 수치해석이나 실험 데이터 분석을 목적으로 사용할 때, 화염 면 법선 벡터는 화염 면 위에서만 존재하며, 국소 지점 주변 영역에서 정의되어 있지 않으므로 엄밀한 연산에서는 $\nabla \circ \vec{n}$ 을 수행할 수 없다. 한편, 앞서 2장 2.2절의 화염 스트레치 모델 식들의 비교를 묘사하는 과정에서 $\nabla \circ \vec{n}$ 은 $\nabla_{s} \circ \vec{n}$ 은 동일함(식 (31))을 보였으며, Matalon과 Candel and Poinsot의 모델 식들(식 (6), (19) 또는 Table 1)을 이용할 때 곡률의 계산을 위해 위 식 (52)를 사용하는 것이 가능하다( $\nabla \circ \vec{n}$ 은 $\nabla_{s} \circ \vec{n}$ 은 동일하지만, 식 (52)의 면-발산 연산을 이용하여 곡률을 계산할 때, 여전히 기준 직교 좌표계 $(x, y, z)$ 를 이용하기보다는 화염 면에 접하는 곡선 직교 좌표계 $(ξ_{1}, ξ_{2}, η)$ 를 이용하여 연산하는 것이 간단하고 명료하다.).

한편, 화염 면의 형상만을 고려하여 유도된 Chung and Law의 모델 식(식 (13), 또는 Table 1)의 경우에는, 면-발산 연산, $\nabla_{s} \circ \vec{n}$ ,을 통해 곡률 𝜅를 정의함이 명시적으로 표현되어 있다. 화염 면 위의 단위 법선 벡터 $\vec{n}$ 과 화염 면 정보만을 이용하여 계산하므로, 수치해석이나 실험 데이터 분석을 목적으로 화염 스트레치를 산출할 때 식 (52)를 이용하여 곡률 𝜅을 간단하고 명료하게 구할 수 있다.

4.4 화염 이동 속도, 유동 속도, 화염 전파 속력의 적용 및 화염 스트레치 산출

앞 절들에서 설명한 화염 면 정의, 화염 면 단위 법선 벡터 $\vec{n}$ , 화염 면 곡률 𝜅 정보들과 화염 면 이동 속도 ${\vec{v}}_{f}$ 를 이용하여 Table 1, 2와 같이 화염 스트레치를 산출할 수 있다. 또는, Table 3과 같이 유동 속도 $\vec{u}$ 와 국소 화염 전파 속력 $s_{L}$ 을 이용하여 화염 스트레치를 산출할 수 있다.

이론적 전개를 목적으로 화염 스트레치를 산출할 경우, 앞서 언급한 바와 같이, (화염 형상 함수 $F (x, y, z, t)$ , 화염 면의 정의(식 (48)), 단위 법선 벡터 $\vec{n}$ 은 전체 공간과 시간에 대해 존재하듯이) 화염 이동 속도 ${\vec{v}}_{f}$ 도 전체 공간과 시간에 대해 벡터장으로 존재한다(화염 이동 속도 ${\vec{v}}_{f}$ 와 연관된 유동 속도 $\vec{u}$ 와 국소 화염 전파 속력 $s_{L}$ 도 전체 공간과 시간에 대해 존재한다.). 따라서, 이러한 속도들에 관한, 화염 면 위의 정보뿐만 아니라 화염 면 밖의 정보를 요구하는, 일반 델 연산자(𝛻)를 이용한 연산이 가능하다. Table 1, 2, 3의 Matalon과 Candel and Poinsot의 모델 식들은 화염 이동 속도 ${\vec{v}}_{f}$ 와 유동 속도 $\vec{u}$ 에 관한 일반 델(𝛻) 연산을 포함하고 있다.

그러나, 수치해석이나 실험 데이터 분석을 목적으로 사용할 때, 앞서 언급하였듯이, 화염 이동 속도 ${\vec{v}}_{f}$ (또는, 이와 연관된 유동 속도 $\vec{u}$ 와 국소 화염 전파 속력 $s_{L}$ )는 화염 면 위에서만 존재하며 국소 지점 주변 영역에서 정의되어 있지 않다. 따라서, 화염 면 밖의 정보를 요구하는, 일반 델 연산자(𝛻)를 이용한 연산이 불가능하다. 한편, 화염 면의 형상만을 고려하여 유도된 Chung and Law의 모델 식(Table 1, 2, 3 참조)의 경우에는, 면-델 연산자( $\nabla_{s}$ )를 사용하여 화염 위의 화염 이동 속도 ${\vec{v}}_{f}$ 와 유동 속도 $\vec{u}$ 에 관한 연산을 수행하며 화염 면 밖의 정보를 요구하지 않는다. 따라서, 수치해석이나 실험 데이터 분석을 목적으로 사용할 때 화염 스트레치를 산출하기 위하여 간단하고 명료하게 적용할 수 있다.

5. 결 론

화염의 형상, 거동, 전파 및 이동 속도 등의 화염의 동역학적 특성들은 연소실 내 연소 및 유동 현상에 영향을 미친다. 화염의 형상 및 분포 변화에 따라 연소실 내의 연소 환경 변화에 영향을 미치므로 연소 효율, NOx, CO, 등 공해 가스 생성 등에 영향을 미친다. 또한, 시-공간적으로 섭동하는 화염의 특성치들은 발생한 화염 및 유동의 거동에 영향을 미치며 역화(flash back), 국소 소염(local extinction), 화염 날림(blow out), 연소 불안정(combustion instability) 등의 현상들과 연관이 있다.

화염의 형상, 거동, 전파 및 이동 등의 동역학적 특성을 연구하기 위한 대표적인 특성치들(characteristics)로는 화염 면의 형상/위치, 화염 전파 속력, $s_{L}$ , 화염 스트레치, $K$ , 화염 면의 곡률, 𝜅, 등이 있으며, 연료의 종류, 혼합 연료의 혼합비, 산화제, 당량비 등의 연료 특성에 따라 영향을 받게 된다. 이러한 특성치들은 정확히 측정되거나 산출되어야 하며, 이 중 화염 스트레치의 산출에 관하여 산출 모델 식들을 조사하고 이론적 연구, 수치해석 및 실험 데이터 분석에의 적용에 관하여 고찰하였다.

화염 스트레치 산출을 위한 대표적인 3가지 모델 식들, i) Matalon, ii) Chung and Law, iii) Candel and Poinsot에 의해 개발된 불변형의 산출 수식들, 을 소개하고 유도과정을 간략히 묘사하였다. 이러한 화염 스트레치 모델 식들은 각각 유도과정과 배경이 다소 차이가 있으며 서로 다른 형태를 가지고 있다. 모델 식들의 명료한 적용을 위하여, 3가지 화염 스트레치 모델 식들의 동일함을 묘사하였다.

화염 스트레치 모델 식들은 화염의 거동에 따른 분류를 이용하여, 화염 면이 (곡률은 유지한 상태로) 화염 면에 접하는 방향으로 이동하며 발생하는 접선 화염 스트레치와 (곡률의 변화와 함께) 화염 면이 화염 면의 수직 방향으로 이동하며 발생하는 법선 화염 스트레치로 분해하여 표현한 식들을 Table과 함께 제공하였다. 또한, 화염의 이동에 기여하는 요인들의 분류를 이용하여, 유동 속도에 기인한 화염의 이동에 의한 화염 스트레치 성분과 연소 현상이 발생함에 따른 화염 전파 속력에 의한 화염의 전파에 의한 화염 스트레치 성분으로 분해하여 표현한 식들도 Table과 함께 제공하였다. 화염의 거동에 따른 분류와 화염 이동 요인에 따른 분류를 모두 적용하여 분해한 표현식들도 Table과 함께 제공하였다.

화염 스트레치 산출 모델 식들을 이론적 연구 목적이나 수치해석 및 실험 데이터의 분석을 위한 목적으로 적용할 때, 특이점과 장단점들을 각모델 식들의 유도 배경과 함께 고찰하였다. 특히, 수치해석 및 실험 데이터를 분석하여 화염 스트레치를 산출할 때, 화염 면의 위치/형상과 화염 면 위에서의 특성치들만 주어지는 경우가 많다. 이 경우에는 화염 면의 위치 및 형상 정보와 화염 면 위에서의 연산만으로 화염 스트레치 산출이 가능한 모델 식을 사용하는 것이 명료한 적용이 가능하다: Chung and Law 모델 식. 그렇지 않은 모델 식들의 경우에는 주어진 화염 면 위치/형상 정보와 화염 면 위의 특성치 데이터만으로는 (미지수의 발생 등으로) 충분하지 않으므로 연산이 명료하지 않으며 추가적인 특성들을 이용하여야 한다: Matalon 모델 식과 Candel and Poinsot의 모델식. 또한, 본 문서에서는 모델 식들을 적용한 화염 스트레치 산출을 위한 자세한 과정들(화염 면 정의, 단위 법선 벡터 설정, 곡률 산출, 화염 이동 속도, 유동 속도, 화염 전파 속력의 적용 등)의 계산과 각 모델 식들의 적용에 관하여 고찰하였다.

본 연구와 함께 제출한 연구, “모델 적용”[24]에서는 수치해석 및 실험을 통해 얻은 화염 및 유동장 데이터를 분석하여 화염 스트레치를 산출하기 위한, 화염 스트레치 모델 식의 적용을 간략히 묘사하였다. 화염 스트레치 모델 식들은 앞서 언급한 바와 같이 표현 형태가 다양하고 데이터에 적용이 명료하지 않거나 연산이 복잡할 수 있으므로, 이를 위한 명료한 산출식을 제공하였다. 화염 스트레치 산출 예시들을 2차원 정상 상태 화염과 비정상 상태 화염에 관하여 제공하였다.

기 호 설 명

$(x, y, z)$ : 직교 좌표계

$(\vec{i}, \vec{j}, \vec{k})$ : 단위 직교 벡터들

$(ξ_{1}, ξ_{2}, η)$ : 화염 면 직교 좌표계

$(\vec{τ_{1}}, \vec{τ_{2}}, \vec{n})$ : 화염 면 직교 좌표계의 단위 직교 벡터들

$\vec{n}$ : 화염 면 단위 법선 벡터

$\vec{τ_{1}}, \vec{τ_{2}}$ : 화염 면 단위 직교 접선 벡터들

$\nabla = \vec{i} \frac{\partial}{\partial x} + \vec{j} \frac{\partial}{\partial y} + \vec{k} \frac{\partial}{\partial z}$ : 델 연산자(직교 좌표계)

$\nabla = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}} + \vec{n} \frac{\partial}{\partial η}$ : 델 연산자(화염 면 직교 좌표계)

$\nabla_{s} = \vec{τ_{1}} \frac{\partial}{\partial ξ_{1}} + \vec{τ_{2}} \frac{\partial}{\partial ξ_{2}}$ : 면-델 연산자

$K_{u}$ : 유동 속도에 의한 화염 스트레치

$K_{n, u}$ : 유동 속도에 의한 법선 화염 스트레치

$K_{τ, u}$ : 유동 속도에 의한 접선 화염 스트레치

$K_{s_{L}}$ : 화염 전파 속력에 의한 화염 스트레치

$K_{n, s_{L}}$ : 화염 전파 속력에 의한 법선 화염 스트레치

$F$ : 화염 형상 함수

${\vec{v}}_{f}$ : 화염 이동 속도

${\vec{v}}_{f, n}$ : 화염 면 법선 화염 이동 속도

${\vec{v}}_{f, τ}$ : 화염 면 접선 화염 이동 속도

$\vec{u}$ : 유동 속도

${\vec{u}}_{n}$ : 화염 면 법선 유동 속도

${\vec{u}}_{τ}$ : 화염 면 접선 유동 속도

$s_{L}^{0}$ : 1차원 0-스트레치 평면 화염 층류 화염 전파 속력

$s_{L}$ : 국소 화염 전파 속력

$K$ : 화염 스트레치

$K_{n}$ : 법선 화염 스트레치

$K_{τ}$ : 접선 화염 스트레치

𝜅 : 화염 면 곡률

$()_{u}$ : 비반응(unburned) 영역의 특성치

$()_{b}$ : 반응 완료(burned) 영역의 특성치

$()_{f}$ : 화염 면 특성치

Acknowledgements

이 논문은 정부(산업통상자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행되었습니다(20206710100060, 분산발전 가스터빈용 수소 전소 저 NOx 연소기 개발, 20214000000310, 탄소중립 고효율 가스터빈 연소기술 에너지 혁신 연구센터).

References

Y. Ju, H. Matsumi, K. Takita, G. Masuya, Combined effects of radiation, flame curvature, and stretch on the extinction and bifurcations of cylindrical CH₄/air premixed flame, Combust. Flame, 116(4) (1999) 580-592. 10.1016/S0010-2180(98)00051-0

A.J. Morales, I.M. Lasky, M.K. Geikie, C.A. Engelmann, K.A. Ahmed, Mechanisms of flame extinction and lean blowout of bluff body stabilized flames, Combust. Flame, 203 (2019) 31-45. 10.1016/j.combustflame.2019.02.002

L.J. Humphrey, V.S. Acharya, D.-H. Shin, T.C. Lieuwen, Modeling the Response of Turbulent Flames to Harmonic Forcing, Combust. Sci. Technol., 189(2) (2017) 187-212. 10.1080/00102202.2016.1202245

G.H. Markstein, Nonsteady Flame Propagation, Pergamon Press, Oxford, (1964). 10.1016/B978-1-4831-9659-6.50005-6

P. Clavin, Dynamic behavior of premixed flame fronts in laminar and turbulent flows, Prog. Energy Combust. Sci., 11(1) (1985) 1-59. 10.1016/0360-1285(85)90012-7

P. Clavin, J.C. Graña-Otero, Curved and stretched flames: The two Markstein numbers, J. Fluid Mech., 686 (2011) 187-217. 10.1017/jfm.2011.318

H.J. Kim, K. Van, D.K. Lee, C.S. Yoo, J. Park, S.H. Chung, Laminar flame speed, Markstein length, and cellular instability for spherically propagating methane/ethylene-air premixed flames, Combust. Flame, 214 (2020) 464-474. 10.1016/j.combustflame.2020.01.011

G.K. Giannakopoulos, A. Gatzoulis, C.E. Frouzakis, M. Matalon, A.G. Tomboulides, Consistent definitions of "Flame Displacement Speed" and "Markstein Length" for premixed flame propagation, Combust. Flame, 162(4) (2015) 1249-1264. 10.1016/j.combustflame.2014.10.015

M. Bozkurt, M. Fikri, C. Schulz, Investigation of the kinetics of OH* and CH* chemiluminescence in hydrocarbon oxidation behind reflected shock waves, Appl. Phys. B: Lasers Opt. 107 (2012) 515-527. 10.1007/s00340-012-5012-y

V.N. Nori, J.M. Seitzman, CH* chemiluminescence modeling for combustion diagnostics, Proc. Combust. Inst. 32(1) (2009) 895-903. 10.1016/j.proci.2008.05.050

S. Hu, J. Gao, C. Gong, Y. Zhou, X.S. Bai, Z.S. Li, M. Alden, Assessment of uncertainties of laminar flame speed of premixed flames as determined using a Bunsen burner at varying pressures, Appl. Energy, 227(1) (2018) 149-158. 10.1016/j.apenergy.2017.09.083

S. Chaudhuri, Life of flame particles embedded in premixed flames interacting with near isotropic turbulence, Proc. Combust. Inst., 35(2) (2015) 1305-1312. 10.1016/j.proci.2014.08.007

B. Karlovitz, D.W. Denniston, D.H. Knapschaefer, F.E. Wells, Studies on Turbulent flames: A. Flame Propagation Across velocity gradients B. turbulence Measurement in flames, Symposium (International) on Combustion, 4(1) (1953) 613-620. 10.1016/S0082-0784(53)80082-2

F.A. Williams, A review of some theoretical considerations of turbulent flame structure, AGARD Conference Proceedings, 164 (1975) 1.

F.A. Williams, Recent Advances in Theoretical Descriptions of Turbulent Diffusion Flames, Turbulent Mixing in Nonreactive and Reactive Flows, (1975) 189-208. 10.1007/978-1-4615-8738-5_5

J. Buckmaster, The Quenching of Two-dimensional Premixed Flames, Acta Astronautica, 6(5-6) (1979) 741-769. 10.1016/0094-5765(79)90031-6

M. Matalon, On Flame Stretch, Combust. Sci. Technol., 31(3-4) (1983) 169-181. 10.1080/00102208308923638

S.H. Chung, C.K. Law, An Invariant Derivation of Flame Stretch, Combust. Flame, 55(1) (1984) 123-125. 10.1016/0010-2180(84)90156-1

S.M. Candel, T.J. Poinsot, Flame Stretch and the Balance Equation for the Flame Area, Combust. Sci. and Tech., 70(1-3) (1990) 1-15. 10.1080/00102209008951608

D.R. Dowdy, D.B. Smith, S.C. Taylor, A. Williams, The use of expanding spherical flames to determine burning velocities and stretch effects in hydrogen/air mixtures, Symposium (International) on Combustion, 23(1) (1991) 325-332. 10.1016/S0082-0784(06)80275-4

E. Varea, J. Beeckmann, H. Pitsch, Z. Chen, B. Renou, Determination of burning velocities from spherically expanding H2/air flames, Proc. Combust. Inst., 35(1) (2015) 711-719. 10.1016/j.proci.2014.05.137

T.M. Vu, M.S. Cha, B.J. Lee, S.H. Chung, Tip opening of premixed bunsen flames: Extinction with negative stretch and local Karlovitz number, Combust. Flame, 162(4) (2015) 1614-1621. 10.1016/j.combustflame.2014.11.022

J. Lambert, S. Coulombe, G. Bourque, J.M. Bergthorson, Investigation of the hydrodynamic effect of nanosecond repetitively pulsed discharges on a laminar stagnation flame, Proc. Combust. Inst., 38(4) (2021) 6567-6574. 10.1016/j.proci.2020.06.166

Y.J. Kim, M. Choi, K. Kim, D.-H. Shin, Comparisons of Flame Stretch Calculation Models and Their Applications, Part II: Model Applications, Journal of The Korean Society Combustion, 28(2) (2023) 38-56.

M.E. Gurtin, A. Struthers, W.O. Williams, A Transport Theorem for Moving Interfaces, Q. Appl. Math., 47(4) (1989) 773-777. 10.1090/qam/1031691

P. Cermelli, E. Fried, M.E. Gurtin, Transport relations for surface integrals arising in the formulation of balance laws for evolving fluid interfaces, J. Fluid Mech., 544 (2005) 339-351. 10.1017/S0022112005006695

R. Fosdick, H. Tang, Surface Transport in Continuum Mechanics, Math. Mech. Solids, 14(6) (2009) 587-598. 10.1177/1081286507087316

P. Lidström, Moving Regions in Euclidean Space and Reynolds' Transport Theorem, Math. Mech. Solids, 16(4) (2011) 366-380. 10.1177/1081286510393805

N. Peters, Turbulent Combustion, Cambridge: Cambridge University Press, (2000). 10.1017/CBO9780511612701

Journal of the Korean Society of Combustion 한국연소학회지 ISSN:1226-0959(Print) 2466-2089(Online)

Preview

Comparisons of Flame Stretch Calculation Models and Their Applications Part I: Model Comparisons

ABSTRACT

MAIN

(1)

Fig. 1.

A schematic of a flame surface showing its curvilinear coordinate system and the reference coordinate system.

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 2.

A diagram of a moving surface in 3-dimensional space.

(14)

(15)

(16)

(17)

(18)

(19)

Table 1.

Flame stretch model equations

(20)

(21)

(22)

(23)

(24)

(25)

(26)

(27)

(28)

(29)

(30)

(31)

(32)

(33)

(34)

(35)

(36)

(37)

(38)

(39)

(40)

(41)

Table 2.

Flame stretch expressions in terms of tangential and normal stretches

(42)

(43)

(44)

(45)

(46)

Table 3.

Flame stretch expressions in terms of flow velocity and flame propagation velocity

(47)

(48)

Table 4.

Surface unit normal vector definition and corresponding curvature, flame shape scalar function, and flame propagation velocity

(49)

(50)

(51)

(52)

Acknowledgements

References