1. 서 론
2. 연구방법 및 실험 장치
2.1 저선회 연소기 구조 및 실험 조건
2.2 프랙탈 형상 격자
2.3 실험 장치 및 진단방법
3. 결과 및 고찰
3.1 저선회기의 비반응 유동장 특성
3.2 저선회 화염의 난류 특성 영역
3.3 난류유동과 저선회 화염의 상관식
4. 결 론
1. 서 론
현재 대부분 가스터빈 연소기가 적용하고 있는 강선회 연소기법에서 발생하는 재순환영역을 제거하기위해 저선회 연소(low swirl combustion, LSC) 방법이 Cheng으로부터 제안되었다[1, 2]. 저선회 화염의 안정화 메커니즘은 기존 강선회 화염과는 다른 원리로 이루어진다. 저선회 연소기술의 핵심 원리는 중앙 채널을 통해 생성된 확대유동이 자유 전파하는 평면 예혼합화염의 특성과 상호작용(interaction)하는 것이다. 확대유동(divergent flow) 형태로 중앙 채널에서 분출되는 예혼합기(premixed mixture)는 노즐 위에서 감소하는 국부 제트속도를 통해 난류화염속도(turbulent flame speed)와 같아지는 지점을 만들어 안정적으로 부상하는 자유 전파화염(freely propagating flame) 형성을 유도한다. 이때 선회부분의 유동은 외부유동과 전단층(shear layer)을 형성하므로, 중앙 유동을 고립시켜 등방성 유동을 보존하는 역할을 한다.
저선회 화염의 난류 구조해석에 대해서 강조되는 장점은 첫째, 높은 난류강도를 가진 등방성 난류유동(isotropic turbulent flow)의 안정적인 화염을 쉽게 형성할 수 있고[1, 2], 둘째, 형성된 제트 부상화염 중앙선 상의 상, 하류 유동장 형태는 정체점을 가진 유동 내 안정화 화염과 굉장히 유사하다는 것이다. 이로 인해 복잡한 난류화염의 특징을 축 방향(axial direction) 1차원 자유 전파화염(1-dimensional freely propagating flame)의 Bray – Moss - Libby 모델과 유사하게 모사하여, 복잡한 난류화염의 구조를 쉽게 파악할 수 있게 된다[3].
난류 예혼합화염에 관한 연구는 다양한 난류화염 형태를 통해서 광범위하게 연구되어 왔다. Frank 및 Kobayasi는 Bunsen 형태의 연소기에서[4, 5, 6, 7], Soika 및 Robin은 막대로 안정화시킨 V 형상의 화염을 통해[8, 9], 그리고 구형 전파 난류화염을 통한 연구는 Bradely 등을 통해서 이루어져 왔다[10]. 마찬가지로 본 연구에서 사용한 저선회 연소기법은 앞서 설명한 장점들에서 확인할 수 있듯이 제트 중심선 상을 기준으로 1차원의 매우 간단한 유동장 형태를 보여주기 때문에 난류 예혼합화염의 구조분석 및 화염속도와 같은 고유 특성을 조사하는 데 매우 적합한 실험장치로 활용되어왔다. 관련 연구로, Bedat과 Cheng은 Laser Doppler Anemometery(LDA)를 이용하여 반응진척도(reaction progress variable)인 = 0.05(화염 선단 영역)의 위치에서 = 1.5 m/s 조건의 난류강도까지 등방성 유동이 생성됨을 확인하고, 고정된 적분 길이스케일(integral length scale)을 이용하여 저선회 연소의 화염구조를 연구했다[1]. 이들은 총 4가지 화염형태를 Borghi-Barrere 선도를 통하여 Kilmov-Williams criterion(Ka≈1) 조건 근처의 화염구조를 분석했다. 이때 난류화염속도는 다양한 화염영역 조건임에도 불구하고, 난류 동적에너지 ()에 선형적으로 증가하는 경향을 나타내었으며, 이러한 결과는 Bradley의 비정상 화염(unsteady flame)을 통한 결과보다 높은 값을 보였다[11]. 나아가 계속된 연구에서, Cheng 등은 LDA와 OH-PLIF을 이용하여, 등방성 유동 내 15 mm로 고정된 적분 길이스케일에서 = 0.2 부터 2.2 m/s 조건까지의 화염구조를 관찰하였고, 과 의 관계가 의 선형적인 상관식으로 관련되는 것을 확인하였다[12]. 이러한 관계는 저선회에서 발생한 등방성 유동장 내에서 로 표현되는 Damkhöler 모델식의 난류 섭동과 난류화염속도 간의 관계가 잘 모사되는 것을 보여준다.
그런데, 저선회 인젝터 경우 난류생성기 역할을 하는 중앙 채널의 격자판(grid plate)을 통해 다양한 난류 길이스케일들이 생성되고 있으며, 이들 상호작용에 의한 난류특성이 저선회 연소성능 및 화염안정화에 결정적인 영향을 미치고 있음[1, 2, 13, 14]에도 불구하고 난류생성기의 격자판에서 생성된 난류 길이스케일들이 저선회 연소에 미치는 영향에 대해서는 아직까지 체계적인 연구가 되어 있지 않았다. 게다가 난류생성기의 격자판 형상이 타공(perforated hole)의 원형(circle) 아닌 프랙탈(fractal, 이하 프랙탈) 형상을 갖는 프랙탈 격자에 대한 연구는 거의 전무한 실정이다. 따라서, 본 연구에서는 저선회 버너에서 주로 사용된 원형의 격자판과 동일한 막힘률을 갖는 프랙탈 구조의 프랙탈 격자를 사용하여 이들 격자들로부터 생성된 난류 적분스케일들이 저선회 난류유동과 화염구조에 미치는 영향을 난류화염 선도를 기반으로 분석하고 이들과 난류연소속도와의 상관관계를 파악하고자 한다.
프랙탈 구조는 기하학적 형상(pattern)이 유지된 채 끝없이 반복되어 되풀이되면서 공간을 부분적으로 채워나가는 구조를 의미한다. 프랙탈 구조의 격자를 통과하는 유체는 일정한 규칙에 따라서 변형되는 크기와 배열로 배치되는 형상을 만나게 되는데, 이때 서로 다른 크기의 격자를 통해 생성되는 다양한 길이의 와류형태가 난류의 동적 에너지를 재분배함으로써 효율적으로 난류강도를 증가시키게 된다. 이처럼 프랙탈 구조의 기하학적인 흥미로운 형상과 함께 프랙탈 격자가 난류강도를 효과적으로 증가시킬 수 있다는 유체공학자들의 연구결과에 착안하여 반응유동장인 화염장에서 프랙탈 격자를 이용한 난류연소 특성에 대한 연구가 최근 들어 진행되고 있다.
Soulopoulos 등은 가는 막대(rod)로 화염을 안정화 시킨 V 형태 예혼합화염(V shape premixed flame)에서 반복되는 사각 형태의 격자를 이용하여 난류강도와 난류화염속도를 관찰하였다[15, 16]. 이들은 화염선단(flame brush) 두께와 곡률(curvature)의 정량적 관찰을 통해서 프랙탈 격자를 통해 증가된 난류강도(turbulent intensity)는 기존의 일반 타공의 원형 격자에서의 화염보다 더 주름지고 강한 화염강도가 나타나는 것을 보였고, 평균적으로 40 % 이상의 난류 연소속도가 증가하는 것으로 보고하였다. Verbeek은 사각 형태와 십자 형태의 프랙탈 격자를 이용하여 V-형태 예혼합화염의 구조에 대해서 Hot wire anemometer(HWA)와 OH-PLIF을 사용하여 조사하였다[17]. 반응진척도인 = 0.5 위치에 해당하는 데이터를 이용하여, 이 난류화염속도의 핵심 인자가 되는 것을 나타내었고, 각기 다른 격자를 통해서 와 난류강도가 격자의 형상에 따라 다르게 발생하고, 형상의 규칙성에 따라서 난류유동을 제어할 수 있다는 것을 보여주었다.
한편 Goh 등은 CH4과 C3H8의 희박 예혼합 대향류 화염(lean premixed opposed jet flames)에서 비교적 단순한 프랙탈 형태의 격자에 따른 반응물과 생성물 내 난류구조를 밀도 분리 방법(density segregation method)를 이용하여 관찰하였다[18]. 이들도 기존 타공판(perforated plate)에 비해 프랙탈 격자는 높은 난류구조를 생성하고 낮은 에너지 감소율을 가지는 것으로 보고하고 있다. 또한, 조건성 적정 직교분리법(conditional proper orthogonal decomposition, CPOD)과 반응진척함수(reaction progress variable function)를 이용하여, 연소가 반응물 유동장에는 미미한 에너지 분배를 보이지만, 당량비의 증가에 따라 생성물 유동에 난류의 동적 에너지의 증가를 확인했다.
언급한 바와 같이, 프랙탈 격자가 지닌 난류성능에서 다양한 장점으로 인해 기본적인 형상에서의 난류 예혼합화염에 관한 연구들이 진행되어 왔지만, 보일러와 가스터빈 연소기에 적용되도록 실제 저선회 인젝터 설계 변수들과 함께 프랙탈 격자 기반의 난류화염 구조에 대해 체계적으로 조사된 연구들은 아직까지 부족한 실정이다. 더군다나 앞서 소개된 연구들에서 난류유동과 난류 예혼합화염의 관계를 관찰할 때, 반응진척도(reaction progress variable)인 = 0.5에서 비(非)반응장 유동의 , 적분 길이스케일(integral length scale)과 국부 비반응장 속도를 국부 변위난류화염속도(local displacement turbulent flame speed)로 이용하고 있다[15, 16, 17]. 결과적으로, 화염의 존재가 고려된 화염 면(flame let) 직전의 위치에서 난류유동과 난류화염속도과의 직접적인 상관관계에 대해서는 좀 더 엄밀한 관찰과 분석이 요구되고 있음을 알 수 있다.
저선회 인젝터 내부의 난류생성판에 프랙탈 형상의 격자를 적용하는 것은 연소에너지 밀도를 향상시켜 저선회 연소기 특징인 부상된 화염의 보염(保焰) 능력을 증대하는 방법으로 예상된다. 따라서 본 연구에서는 확대유동을 형성하는데 핵심적 역할을 하는 난류생성판의 형태를 다양한 함수를 가진 프랙탈 형상으로 적용하여 유동성분 및 난류스케일에 대한 연소성능의 응답을 난류화염속도와 관계 지어 관찰하고자 한다. 이를 위해 먼저 비반응 유동장(non-reacting flow field)에서 2D-HWA를 이용하여, 저선회 유동의 큰 특징인 자기상사성(self-similarity) 현상이 기존 타공(perforated hole) Hexa. 형상과 프랙탈 격자에서도 동일하게 발생하는 것을 확인한다. 세부적으로는 프랙탈 격자들의 두께축소율에 따라 변경되는 난류평균유속과 난류변동성분을 통해 난류생성판을 지나서 발생하는 웨이크 상호작용이론(wake interaction theory)을 관찰하고, 프랙탈 격자를 통해 발생하는 다양한 유동 길이스케일의 상호작용에서 유발된 난류강도(turbulent intensity, )와 난류에너지(turbulent energy, )를 확인한다. 이어서 LDV 기반의 레이저 진단법을 통해 화염선단(leading edge of flame brush)에서 취득한 유동성분들과 당량비에 따른 화염의 물성치를 이용하여 대표적인 난류화염 분류법인 Borghi – Peter 선도에서 난류생성판의 형상에 따라 발생하는 화염의 구조적 영역을 분류한다. GRI 3.0을 이용하여 수치적으로 계산된 층류연소속도에 따른 난류화염속도의 거동을 관찰하고, 프랙탈 형상의 격자에서 발생한 다양한 난류유동성분과 국부 평균난류화염속도(local mean turbulent flame speed)를 이용하여, 기존 R.K. Cheng이 제안한 의 관계를 확인한다. 나아가서 화염브러쉬 기저(flame brush base) 선단에서의 유동과 화염이 갖는 길이스케일 비(比)와 유동섭동과 화염의 속도성분과의 비로 결합되어 무차원화 된 난류 Reynolds 수인 ReT와 난류화염의 응답을 면밀하게 분석한 실험적 상관식 연구(empirical correlation study)를 통해 난류화염 속도에 난류강도뿐만 아니라 난류 길이스케일이 미치는 영향에 대해서 함께 규명하고자 한다.
2. 연구방법 및 실험 장치
2.1 저선회 연소기 구조 및 실험 조건
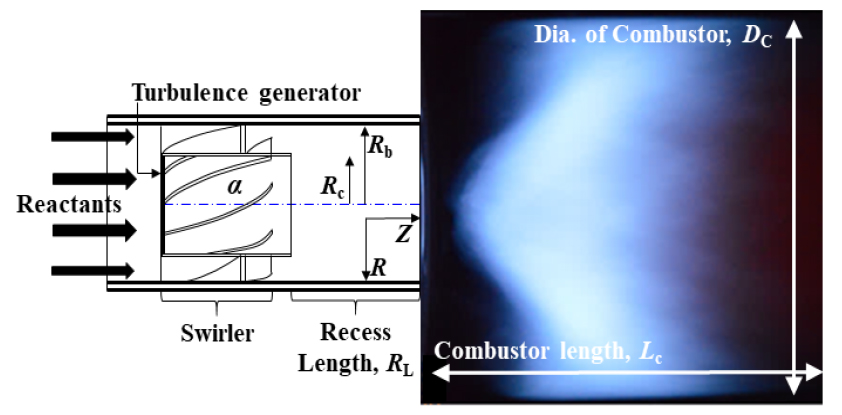
Fig. 1은 본 연구에서 사용되는 저선회 연소기 노즐 개략도와 전형적인 저선회 화염의 형상을 보여주고 있다. 난류유동을 형성시키기 위해 일정한 막힘률을 가진 난류생성판(turbulent generating plate)은 Fig. 2와 같은 형상으로 원형 관(tube)의 맨 아래에 직경 20 mm, 두께 1 mm를 가지고 장착이 된다. 원형 관 외부로는 일정한 선회 각을 가지는 날개가 위치하여 선회 방향의 유동을 형성시킨다. 튜브 끝부터 노즐출구까지는 완화길이(recess length)를 통하여 중앙 채널 유동과 선회 유동의 상호작용을 유도한다.
앞서 설명한 것과 같이 저선회 화염 안정화 메커니즘의 핵심은 원형 관 중앙의 난류생성기(판)를 통과하는 비 선회유동()과 난류 생성기가 장착된 관 외부의 선회 날개를 통과하는 선회 유동()과의 질량 분배율()이 적절히 균형을 이룰 때, 혼합기 유동이 완화 길이(RL)를 통과하여 연소실에서 확대유동을 형성하고, 후류에서의 와류 붕괴(vortex breakdown)를 억제하는 것이다. 이때 발생한 확대유동을 가진 미연 혼합기는 노즐 출구 이후 속도 감소율을 보이며, 난류 예혼합화염 속도와 혼합기의 유동 속도가 같은 지점에서 저선회 연소의 특징인 부상된 화염을 형성하게 된다.
본 연구에서 사용된 저선회 인젝터(low swirl injector, 이하 LSI)의 노즐 출구 직경(D)은 28 mm이고, LSI 이후 노즐 출구까지의 거리인 완화 길이(RL)를 33.5 mm로 하여 적절한 높이의 부상 화염을 형성하기 위한 속도 감소 거리로 고려하였다. 노즐 이후에는 가스터빈 연소실을 모사한 직경(DC) 70 mm, 길이(LC) 300 mm의 석영관(quartz)이 설치되었다. 난류생성판의 막힘률(blockage ratio, )은 난류생성판 면적 대비 프랙탈 격자의 면적을 의미하며, 본 연구에서는 전체 난류생성판의 막힘률()을 70%로 고정하였다. 저선회 연소기의 선회강도(S)를 이전 연구들과 동일하게 식 (1)을 통해 산출하였다[19].
식 (1)에서 은 중앙 유동 채널의 반경()과 노즐 반경()과의 비이며 0.75를 이용하였다. 선회기 각도()는 37°로 고정하여 R.K. Cheng이 제안한 LSI의 설계 가이드 범위를 따랐다[19, 20]. 또한 식 (1)에서 은 질량 유량비()로 는 중앙 채널의 난류생성판을 통과하는 혼합기 질량 유량, 는 선회기 부분을 통과하는 혼합기 질량 유량이다. 이때 연료와 공기는 버블 메타로 교정된 유량 조절기(mass flow controllers, M3200VA [1.5 ~ 50 slpm], VIC-D145 [20 ~ 1,000 slpm], ≤± 1.0% accuracy)를 통해서 예혼합기에서 충분히 혼합된 후 LSI로 공급된다. 저선회 연소기의 선회 강도를 구하기 위한 은 중앙 유동과 선회 유동의 흐름을 각각 막은 후 압력 차 측정을 통해 구하였다. 측정된 을 통해서 이후 설명될 프랙탈 격자별 선회 강도()를 구하였다. 본 연구에서 사용되는 직교(cross)형태의 프랙탈 격자가 적용된 난류 생성판에서 선회각도는 혼합기 평균 속도가 4 ~ 6 m/s까지 감소하다가 8 m/s 이후 0.475 ~ 0.5 값으로 포화(saturation)하는 현상을 보였다. 이러한 현상은 프랙탈 격자의 형태와 상관없이 동일한 막힘률을 가진 난류 생성판에서 유량의 증가는 일정 압력 포화점까지 코어 유량의 증가를 유도하고, 일정한 속도 이후에는 LSI에서 발생하는 선회와 비선회 유동의 유량비()가 일정하게 유지되는 것을 의미한다. 따라서 높은 유속조건(본 연구에서 8 m/s 이상)에서 선회 강도가 일정해지는 점을 고려해서 입구 유속(bulk velocity, )을 10 m/s로 고정하였으며, 당량비()는 0.7 ~ 0.9 범위에서 0.05 간격으로 조사하였고 희박 가연한계 근처 시 발생하는 간헐적인 불안정 현상을 제외함으로써 LSI 화염의 특징인 안정적인 부상 화염 상태에서 분석하였다.
2.2 프랙탈 형상 격자
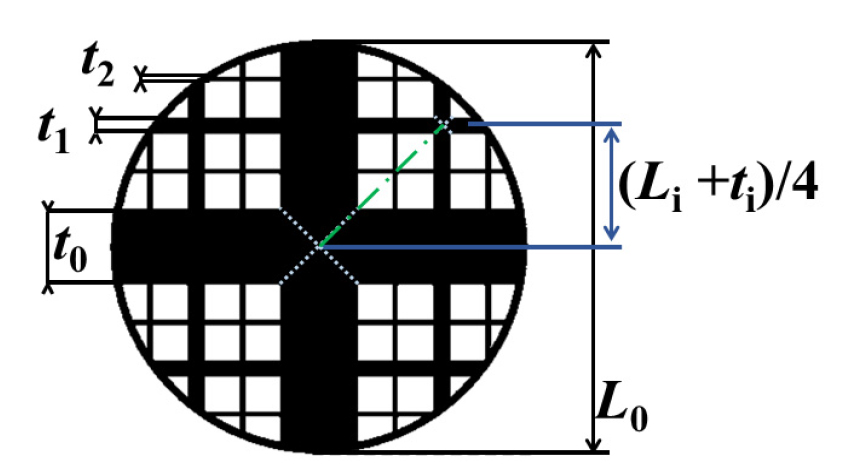
저선회기에서 가장 중요한 구조적 변수인 난류생성판의 형태에 프랙탈 함수를 내포한 구조를 적용하기 위해, 직교(cross) 형태의 격자를 이용하였고, 구조적 정의를 Fig. 2에 나타내었다. 총 3번의 격자 축소 반복과 저선회 난류생성판 적용을 위해서 20 mm 직경의 원형으로 생성되었다. 각각의 격자는 총 4가지의 변수로 완전하게 정의가 된다.
가장 굵은 격자 막대의 길이인 L0와 프랙탈 패턴의 반복 횟수 N, 가장 두꺼운 격자 막대의 두께 t0, 그리고 다음 차수로의 두께 감소비(reduction ratio of bar thickness, 이하 RRBT)로 나타내어진다. 격자들의 배치는 가장 큰 두께의 십자 t0를 그린 후 t1과 t2의 두께를 가진 십자가 (Li + ti)/4 위치에 배열된다. 여기서 i는 격자의 순서를 의미한다. 정해진 위치에 따라 배치되는 격자의 두께는 다음 식 (2)를 통해서 구조적 함수를 가지며 결정된다.
본 연구에서는 격자들의 두께가 줄어드는 비율인 RRBT에 따라 나눈 0.2, 0.4, 0.6, 0.8의 4개의 프랙탈 격자와 멀티스케일을 생성하지 않는 일반적 교차 격자(classical cross)인 RRBT 1.0, 그리고 이전 연구[13]에서 안정화 영역이 가장 넓다고 판단되었던 원형 타공 형태인 일반(normal) 난류생성판으로 Hexa. 형상의 격자가 사용되었고, Table 1에 보여지는 것과 같이 동일한 37°의 선회각도()를 가진 LSI의 노즐 튜브의 상류에 적용된다. 장착된 프랙탈 형상의 격자는 웨이크 상호작용 이론(wake interaction theory)을 통해 유동스케일 간의 상호작용을 극대화하여 난류강도를 증가시킬 것으로 기대가 되고, 난류강도에 비례하는 난류화염속도를 증가시켜 저선회 화염의 안정화에 미치는 영향을 확인하고자 한다.
2.3 실험 장치 및 진단방법
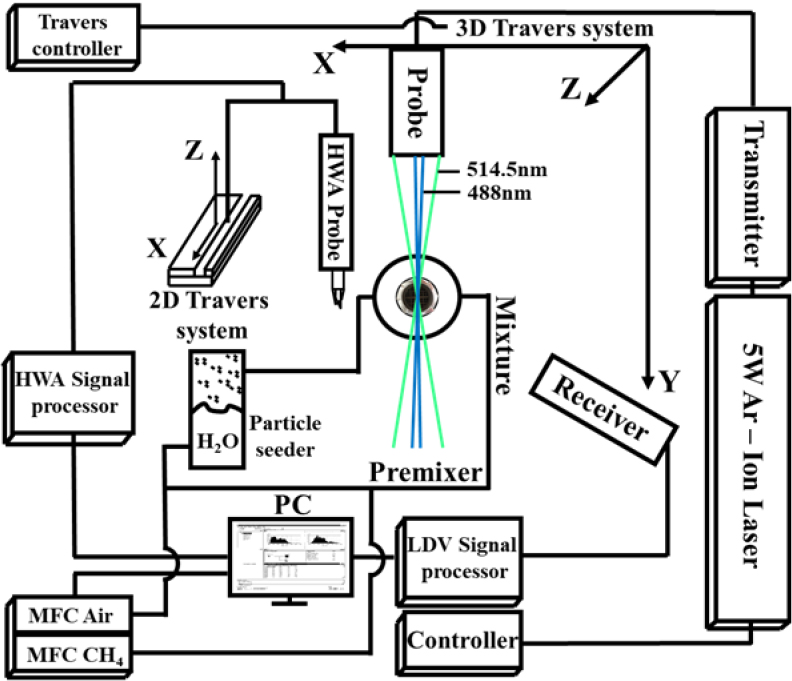
Fig. 3은 본 연구에서 사용된 저선회 연소기의 비반응(non-reacting)과 반응장(reacting field) 난류유동성분을 측정하기 위해서 사용된 2D 열선 유속계(hot wire anemometry, 이하 HWA, TSI - IFA300)와 LDV 시스템의 개략도이다. 비 반응장 유동의 국부적 난류 성분을 측정하기 위해서 HWA의 4 µm 프로브(platinum coated tungsten wire)를 constant temperature anemometer(CTA)와 연동하여 정밀한 계측을 진행하였다. 축 방향(axial direction) 평균속도, 와 난류속도섭동, 은 난류생성판으로부터 105 mm까지 측정되었으며, 데이터 샘플링 주기는 1 kHz로 약 30초간 측정하였다. 측정된 데이터는 5분 동안 취득한 데이터와 비교에서 기준 0.5%, 기준 1% 내외의 차이를 보여줌으로써 프랙탈 함수의 격자를 통해서 생성되는 다양한 스케일을 측정하기에 충분한 것으로 판단하였다. 에너지 스펙트럼을 얻기 위해서 연소 시 평균 화염 선단이 위치하게 되는 노즐 출구 이후 10 mm 위치에서 50 kHz의 높은 측정률(sampling rate)로 300초 간격으로 취득하였으며, 이는 콜모그로브 스케일(Kolmogorov scale)의 주파수인 까지 충분히 측정이 가능한 조건임을 확인하였다[21]. 여기서 는 콜모그로브 길이스케일이다. 이렇게 측정된 속도성분들은 비반응장 저선회 유동의 평균 난류유동속도(), 난류 속도섭동() 그리고 난류에너지 스펙트럼() 분석에 이용된다.
LDV 장치는 반응장 유동의 속도성분을 측정하기 위해서 사용되었다. 5W Ar-Ion Laser(spectra-physics, stabilite 2017)를 통해서 생성된 레이저는 514.5 nm 파장의 녹색 쌍과 488 nm 파장의 청색 쌍의 레이저로 분기된다. 5.27 µm의 플린지(fringe) 영역을 지나는 입자를 통해 산란된 레이저는 400 mm의 초점 거리를 가진 프로브를 통해서 취득된다. 유동 추종 입자는 H2O droplets 챔버를 통해 생성되어, 공유된 유로에서 공기와 함께 연소기로 투입된다. 이때 투입되는 H2O droplets는 10 m/s 기준 질량유량의 1%의 양에 해당한다. PDPA 기능의 LDV 시스템(Dantec, BSA P60)을 통해서 측정된 평균 입자크기는 3 µm를 가지고 연소기 출구로 분출되며, 이때 입자들의 유동 추종성 검토를 위해 계산된 Stokes 수는 Hexa. 형상의 난류생성판을 이용하였을 때, 4 ~ 16 m/s에서 0.05 ~ 0.35의 값을 가졌다. 이러한 결과는 Tropea 등으로부터 제안된 1의 이하를 값을 보이므로, 저선회 연소기에서 발생하는 확대유동(divergent flow)의 속도장 및 유동 특성을 충분히 추종하게 된다[22]. 연소기 중앙선에서 흐르는 입자들을 따라 측정되는 유동 속도는 화염 면까지 3 kHz 이상의 취득률(sampling rate)과 90% 이상의 검증률(validation rate)을 유지하며 측정을 진행하였고, 측정된 데이터는 반응장에서의 과 적분 길이스케일(integral length scale, )을 구하기 위해 사용된다.
3. 결과 및 고찰
3.1 저선회기의 비반응 유동장 특성
본 절에서는 저선회 연소기에서 발생하는 기본적인 유동형태인 확대유동(divergent flow)과 제트 상사성(similarity) 현상을 확인하고, 내부에 장착된 프랙탈 및 기존 타공판 형상의 격자가 노즐 출구 전후의 난류유동에 미치는 영향을 파악하기 위해 먼저 노즐 중심선 기준 축 방향(Axial direction)을 따라서 형성된 비(非) 반응장(nonreacting flow field) 유동의 구조를 조사하였다. 이를 위해 앞절에서 기술하였듯이, 선회 수가 포화하는 조건인 난류생성판 이전 투입 유속(, bulk velocity)을 유량 기준 10m/s로 고정하였고, 난류성능을 평가할 수 있는 주요 항목들인 난류평균속도(), 난류속도섭동(), 난류강도(), 난류에너지 스펙트럼()들을 조사하였다.
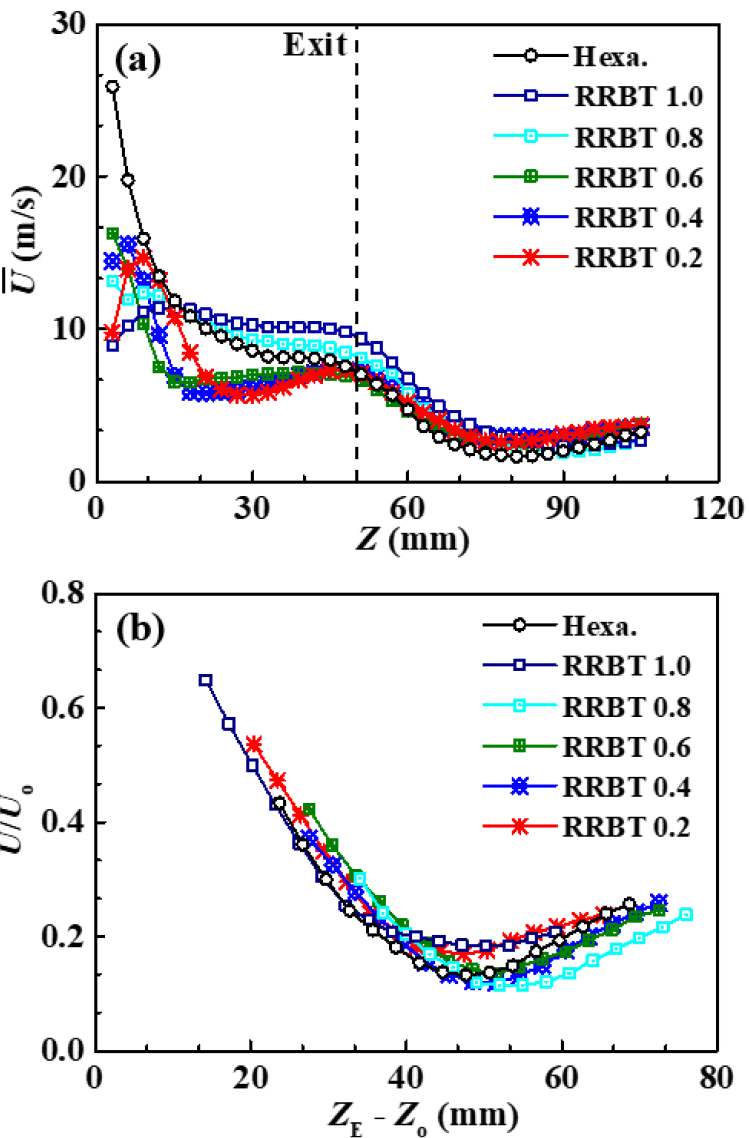
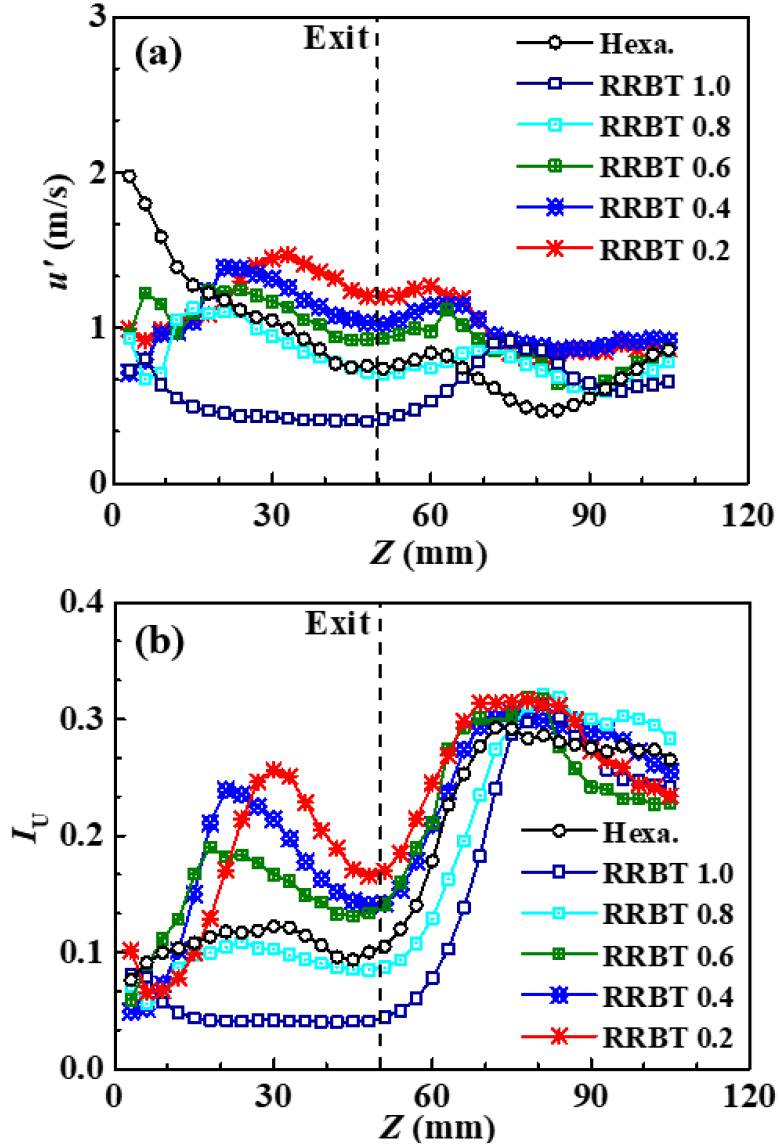
Fig. 4(a, b)는 노즐 중심축에서 축 방향인 Z축 값에 따라 측정된 RRBT 별 프랙탈 격자와 Hexa. 형상 격자의 난류평균속도()와 노즐 출구 이후 발생한 속도 확대율(divergence rate)을 보여준다. 여기서 Z = 0의 위치는 난류생성판의 지점이며, Z = 50은 LSI 연소기의 덕트면으로 노즐 출구 지점을 의미한다. 모든 측정은 Z축 방향으로 3 mm 간격으로 105 mm까지 측정하였으며, 난류생성판에의한 HWA의 프로브(probe) 손상 방지를 위하여 Z = 3 mm부터 측정을 시작하였다.
일반적으로 강선회 인젝터(high swirl injector, 이하 HSI)는 선회기로 발생하는 강한 전단층(shear layer)으로 인하여 중앙 선상 음(-)의 속도가 분명하게 생성되는 것과 달리, 중앙 채널을 통해 발생한 확대유동을 가진 LSI는 최소 유속을 보여주는 Z = 2.85D 위치인 80 mm 부근에서도 양(+)의 속도 분포를 하고 있음을 볼 수 있다. 이러한 속도분포는 사용한 전체 LSI의 난류생성판 조건에서도 확인할 수 있었다. 위와 같은 결과는 저선회 연소기 유동의 특징인 확대유동으로 인해 내부 재순환 영역(inner recirculation zone, 이하 IRZ)이 없는 속도분포를 잘 보여주는 결과이다. 축 방향에서 나타난 의 특징은 난류생성판 이후 급격하게 감소하여 노즐 출구를 벗어나는 Hexa. 경우와 RRBT 1.0 ~ 0.8의 프랙탈 격자인 경우 원점부터 출구 이후까지 지속적으로 감소하는 경향을 보이는 반면, RRBT 0.6 ~ 0.2의 경우 평균속도는 작아지는 RRBT에 따라 멀어지는 최저 속도위치를 가진 이후 Z = 30 ~ 50 mm까지 증가하는 현상을 나타냈다. 이후 노즐 출구 면인 연소기 덤프면 이후에는 확대유동의 특성을 나타내며 감소하다가, 선회 유량의 영향으로 80 mm 이후에는 동일한 유속으로 포화되는 것을 관찰할 수 있다. 흥미로운 점은, 프랙탈 격자 구조의 경우 RRBT가 작아짐에 따라 첫번째 격자의 두께는 증가하게 되고, 이에 따라 최소 이 점진적으로 먼 위치에서 발생하는 것을 확인할 수 있다. 이러한 현상은 웨이크 상호작용 이론(wake interaction theory)을 통해서 이해할 수 있다.
Mazellier 등으로부터 제안된 웨이크 상호작용 이론은 사각(square) 프랙탈 격자에서 격자의 길이(L)와 두께(t)에 의해 발생하는 웨이크가 만나는 지점의 위치가 결정되는 것으로부터 설명된다 [23, 24]. 격자를 구성하는 각각의 L과 t로 인하여 발생하는 다양한 후류 와류 박리(vortex shedding)는 와류 스케일 간의 혼합을 통하여 난류강도를 증가 또는 감소시킬 수 있다. 이때 와류 길이를 특정 격자 길이 L로 가정하였을 때, 가장 큰 와류가 후류에서 만나는 길이를 의미하는 Z*는 가장 큰 격자의 길이 L0와 두께 t0의 비율, Z*= L02/t0의 관계를 가진다. 이렇게 정의된 Z*는 프랙탈 격자에서 발생하는 후류 유동장을 특성화하는데 사용된다. 본 논문에서 사용된 직교(cross) 프랙탈 격자의 형상에서 미루어 보았을 때, 격자의 두께에 의해 와류가 발생하는 직교 프랙탈 격자에서 발생하는 Z*는 가장 두꺼운 격자의 t0에 관계되는 것으로 예상된다. 프랙탈 형상을 LSI의 난류생성기로 적용했을 때 격자마다 다른 Z*의 발생은 다양한 와류 스케일들의 상호작용을 형성하고, 이는 후류에서 난류강도의 변화를 유도하게 된다. 따라서 Fig. 4(a)에서 감소하는 RRBT에 따른 최소 발생 지점의 지연 현상은 두꺼워진 격자의 두께(t)로 인해서 와류가 교차하여 낮은 유속을 가지는 Z*가 점차 먼 지점에서 발생하기 때문으로 이해할 수 있다.
노즐 출구 전 프랙탈 격자를 통해 다양한 위치에서 최소 를 보여준 후 출구 이후 넓어진 연소기 면적으로 인해 모든 경우에서 속도 감소 영역을 Z = 80 mm 지점까지 보여주고 있다. 저선회 확대유동의 주요한 특징인 자기 상사성(self similarity)의 특징을 프랙탈 격자에서 확인하기 위해 LSI 제트의 가상원점(virtual origin, Zo)을 취득하여 보정한 데이터를 Fig. 4(b)에 도시하였다. 제트의 가상원점(Zo)은 제트 유동에서 실제로 속도가 감소하는 위치를 의미하는 것으로, 겉보기 노즐 출구 위치인 ZE 이후 일정한 축 방향 확대율(axial divergence rate, ax = )로 감소하는 을 상류 방향으로 외삽(extrapolation)하였을 때, 1이 되는 위치로 정의된다. 중심선상으로부터 얻어지는 위 두가지 위치는 저선회 유동장의 큰 특징인 상사성 특징을 나타낸다. Cheng은 자기 상사성(self similarity)을 가진 저선회 화염의 유동장 형태를 식 (3)과 같이 제안하였다.
여기서 Zf는 화염의 전단면의 위치, 은 난류화염속도, 은 신장되지 않은 층류 연소 속도를 의미하며, 값은 실험적으로 얻어진 연료 물성치에 대한 상수이다[25, 26]. 식을 보았을 때, 과 는 선형적인 의존성을 가지는 것을 볼 수 있다. 이 경우 화염의 위치(Zf)에서 가상원점(Zo)과 축 방향 확대율(ax)과 결합되고, 이것이 난류강도와 층류연소속도()와 상관식을 구성하므로 넓은 범위의 유속과 당량비 조건에서도 화염의 위치가 일정하게 유지되는 자기 상사성의 특징을 만들어내게 된다.
Fig. 4(b)에서 음의 위치로 발생한 Zo를 ZE에 보상하여 관찰하였을 때, ax = -0.016 ~ 0.018 mm-1의 근소한 확대율(divergence rate) 차이를 보이며, 가상원점이 보상된 좌표에서는 프랙탈 형상의 격자와 Hexa. 형상 격자의 속도 유선이 중첩되어 ZE - Zo = 50 mm 근처에서 최소 가 자리하게 되는 것을 확인할 수 있었다. 이러한 특징을 통해 다양한 난류강도를 생성하는 프랙탈 격자에서 기존의 Hexa. 형상 격자의 연구 결과[25, 26, 27]와 마찬가지로 저선회 연소기의 큰 특징인 자기 상사성을 추종하는 것을 확인할 수 있다. 자기 상사성은 유속의 변화에 따라 가상원점과 축(axial) 방향 확대율이 유기적으로 움직여 넓은 유속 범위에서도 일정한 화염높이를 가지게 되는 원리로 저선회 화염의 안정화 메커니즘으로 설명된다. 난류평균속도의 분포로 나타내어진 상사성 특징이 저선회 내부의 난류생성판 구조를 동일한 막힘률의 프랙탈 형태를 이용하였음에도 잘 형성되는 것을 관찰할 수 있었다. 하지만 프랙탈 격자가 생성한 다양한 난류강도에 따라서 발생하는 유동과 화염 간의 관계를 파악하기 위해서는 RRBT에 따른 난류 성능의 거동을 확인하여야 한다.
저선회 화염의 유동장 형태를 설명하는 식 (3)을 보면, 난류화염속도는 와 비례하여 작용한다. 나아가 프랙탈 격자는 다른 두께의 격자를 지나서 발생하는 다양한 유동 길이 간의 상호작용을 통해 난류 성능을 증가시키므로, RRBT에 따른 의 영향을 확인할 필요가 있다. Fig. 5(a, b)는 중심선인 Z축 방향으로 난류변동성분인 와 길이 방향 난류강도인 의 값들을 보여주고 있다. Fig. 5(a)에서 보여진 Hexa. 격자의 은 노즐 출구(Z = 50 mm)까지 RRBT 0.6과 0.8 사이에서 약한 상승 이후 지속적으로 감소하는 거동과 함께 노즐 출구 이후에 한번의 고점(peak point)을 보인 후 다시 감소하는 현상을 보여주고 있다. 반면 프랙탈 격자의 경우 RRBT 0.2 ~ 1.0까지 격자의 두께에 따라 원점으로부터 먼 위치에서 차례대로 첫번째 고점을 가진 다음 노즐 출구에서 가까운 순서로 두번째 고점을 가지는 흥미로운 현상을 보여준다. 먼저 Hexa. 형상과 프랙탈 격자에서 나타나는 노즐 출구 이후에 고점을 형성하는 원인은 넓어진 연소실 면적으로 인해 감소된 유속과 의 영향보다, 중앙 채널 유동을 서서히 감싸는 약한 선회류의 효과로 인하여 갑작스러운 퍼짐 현상 없이 난류화가 가속되기 때문으로 판단된다. 이때 고점이 발생되는 순서는 약한 선회류와 중앙 유동의 상호작용으로 발생하는 것으로 이해된다. 강조할 부분은 RRBT가 작을수록 노즐 전의 의 첫번째 고점이 상대적으로 늦게 발생하는 것이다. 의 RRBT의 감소에 따라 고점이 지연되는 현상은 둔체 뒤에서 박리된 와류가 만나는 지점이 둔체의 두께에 비례하는 것으로 이해할 수 있고, 이는 마치 굵은 둔체 뒤의 그림자가 후류로 길게 발생하는 것과 유사하다. 따라서 작아지는 RRBT에 따라 첫번째 격자의 두께는 두꺼워지므로 둔체로 인해 길어진 전단층 교차점과 혼합 길이스케일은 다양한 난류 스케일이 상호작용할 수 있는 경우를 증가시켜 난류 유동을 강화한다.
RRBT의 감소에 따른 난류강도 상승 현상에 대해 면밀한 분석을 위해 난류변동성분과 평균속도의 비로 나타내는 난류강도( = )를 Fig. 5(b)에서 확인해보았다. 축 방향 중심축 거리에 따라서 측정된 는 난류변동성분의 경향과 유사하게 Hexa. 형상의 격자에서는 RRBT 0.6과 0.8의 사이에서 발생하는 것을 알 수 있고, 첫번째 고점은 아주 약하게 발생한 후 출구 이후 두번째 고점을 가지는 현상을 보였다. RRBT 0.2 ~ 0.6의 경우 노즐 출구 전 첫번째 고점은 의 경향과 유사하게 RRBT가 작아짐에 따라 큰 값을 가지고 먼 위치에서 발생하지만, RRBT 0.8과 1.0은 에 비해 낮은 값을 가지므로, 첫번째 고점이 뚜렷하게 관찰되지 않았다. 나아가서 노즐 출구 이후 Z = 2.7 ~ 2.8D에서 발생한 최대 강도는 평균적으로 부상된 화염의 기저가 위치하는 Z = 1.7 ~ 2.1D와 비교하였을 때 상당히 원거리에 위치하고 최저 의 위치와 일치하므로, 이러한 현상은 단순히 노즐 출구 이후 급격하게 줄어든 평균속도로 인해 발생한 것으로 판단된다. 여기서 프랙탈 및 Hexa. 형상 격자의 노즐 출구에서 발생하는 화염 기저의 부상 높이가 Z = 1.7 ~ 2.1D인 것을 고려하였을 때, 해당 지점에서 발생하는 난류강도의 비교는 저선회 난류화염의 안정화에 중요한 의미를 갖게 된다. 화염 기저가 위치하게 되는 곳에서 비교된 는 노즐 출구 직후부터 차이를 보이게 되는데, RRBT 0.2 기준의 프랙탈 격자는 해당 영역에서 Hexa. 형상의 격자보다 약 40 ~ 54%의 증가분을 보였다. 식 (3)에서 보여진 길이 방향 난류강도( = )와 난류화염속도()의 선형적 관계를 염두하고 생각하였을 때, 프랙탈 형태의 격자 사용으로 우수해진 는 저선회 연소장의 난류화염속도()를 증가시켜 화염안정화에 유리하게 작용될 것으로 예측이 된다.
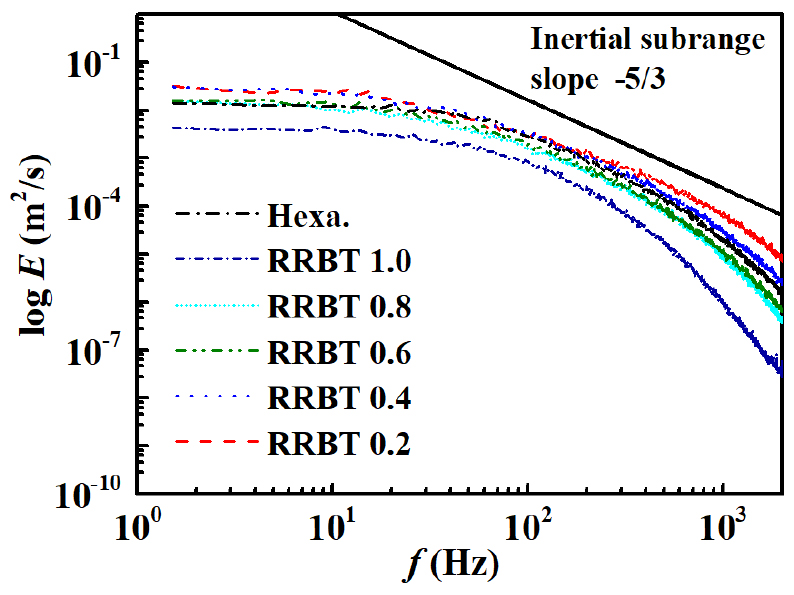
프랙탈 형상으로 증가된 난류 성능을 전체 에너지 영역 기준으로 관찰하기 위하여 속도 신호의 에너지 스펙트럼()을 로그 배율로 Fig. 6에 나타내었다. 막힘률 70%의 난류생성판이 장착된 연소기의 평균 화염 기저 위치는 대략 Z = 2.1D에서 발생하므로, 노즐 중심선상 출구 기준 10 mm 위치에서 50 kHz의 취득률(sampling rate)을 이용하여 유동의 가장 작은 길이스케일인 콜모그로브 길이스케일(Kolmogorov length scale)의 영역까지 에너지가 소산되는 현상을 관찰할 수 있도록 하였다. 결론적으로 전체 주파수 영역에서 프랙탈 격자의 RRBT가 줄어듦에 따라서 난류가 강화되었음을 분명하게 보여주고 있다. Hexa. 격자의 경우 낮은 주파수 영역에서 RRBT 0.6, 0.8과 비슷한 위치에서 발생하였지만, 높은 주파수 영역에서는 위 두 가지 격자보다 높은 에너지를 가지면서 먼 주파수까지 소산되는 것을 볼 수 있다. 앞서 과 의 결과에서 보았듯이, 프랙탈 격자의 경우 화염 기저의 평균 위치에서 RRBT의 감소에 따라서 더 높은 에너지를 가졌다. RRBT 0.2에서 0.4는 Hexa. 격자보다 더 높은 주파수 영역까지 에너지를 효과적으로 전달하는 것을 확인이 되었지만, RRBT 1.0의 경우는 난류에너지가 낮은 주파수부터 낮게 발생하여 높은 주파수까지 현저히 낮은 에너지를 가지는 것으로 확인되었다. 프랙탈 격자를 이용하여 발생된 난류에너지 상승 현상은 높은 주파수에서 확연히 관찰되는데, 약 1000 Hz 이상의 더 높은 주파수 영역에서는 RRBT의 감소에 따라 증가된 난류 흐름을 통해 유동의 프랙탈화(fractality) 효과가 명확히 발생하는 것을 관찰할 수 있다. 나아가서, Hexa. 형태의 격자를 포함한 모든 난류생성판의 에너지 스펙트럼들은 에디(eddy)들의 관성 영역(inertial range)의 큰 특징인 콜모그로브 -5/3 멱함수(power law) 법칙을 약 10 Hz 정도의 다른 주파수 영역에서 추종한다는 것을 관찰할 수 있다[23]. 그러나, 프랙탈 격자의 주요 특징인 격자 후류 난류에너지 감소 영역에서 발생하는 비 평형 소산(non-equilibrium dissipation) 영역의 길어짐 효과와 Richardson – kolmogorov 소산 이론에서 가정되는 소산 계수(dissipation coefficient, )가 일정하지 않고, 1 / Reλ의 거동을 보이는 현상은 감소 영역의 위치, 유속, 저선회 연소기 내부의 유동 영역을 분할하여 상세하게 관찰하여야 하므로, 추가적인 연구가 필요하다[24].
3.2 저선회 화염의 난류 특성 영역
난류 예혼합연소에서 가장 중요한 난류화염속도()에 대한 특성을 파악하는 것에 있어서, 구형 전파 화염, V형 화염, 분젠 화염 등의 연소 구조는 난류강도(turbulent intensity)의 정도에 따라서 등방성 유동(isotropic flow field)을 유지하는 것이 까다로워지므로 난류화염을 명확히 분석하는 데 어려움이 있었다. 앞서 언급한 바와 같이, 저선회 연소기의 장점은 높은 난류강도를 가진 등방성 난류유동에서 안정적인 화염을 쉽게 형성할 수 있고[1, 2], 일정한 속도 감소율을 가지는 중심선상의 유동장을 매우 간단한 형태의 식으로 표현 가능한 것에 있다. 게다가 노즐로부터 안정적으로 부상된 화염 형태를 유지할 수 있어 화염 중앙에서 자유 전파하는 예혼합화염 특성을 레이저를 통하여 쉽게 계측할 수 있다. 따라서 이번 절에서는 LSI 내부에 위치하는 난류생성기(판)에 프랙탈 형상과 타공의 Hexa. 형상을 적용하였을 때, 얇은 반응 영역(thin reaction zone)에 존재하는 난류화염의 특성을 화염 전단면의 난류 유동 정보와 비교하여 상관관계를 제시하고자 한다. 이를 위해 본 논문에서는 10 m/s로 고정된 유속에서 Hexa. 형상과 프랙탈 형상의 저선회 화염을 당량비() 0.7부터 0.9까지 0.05 단위로 조사하여 Fig. 7에 나타내었다. 이 경우 당량비 조건은 희박 가연 한계 근처 시 발생하는 간헐적 불안정 현상을 제외한 안정적인 부상 화염 상태가 유지되는 조건이다.
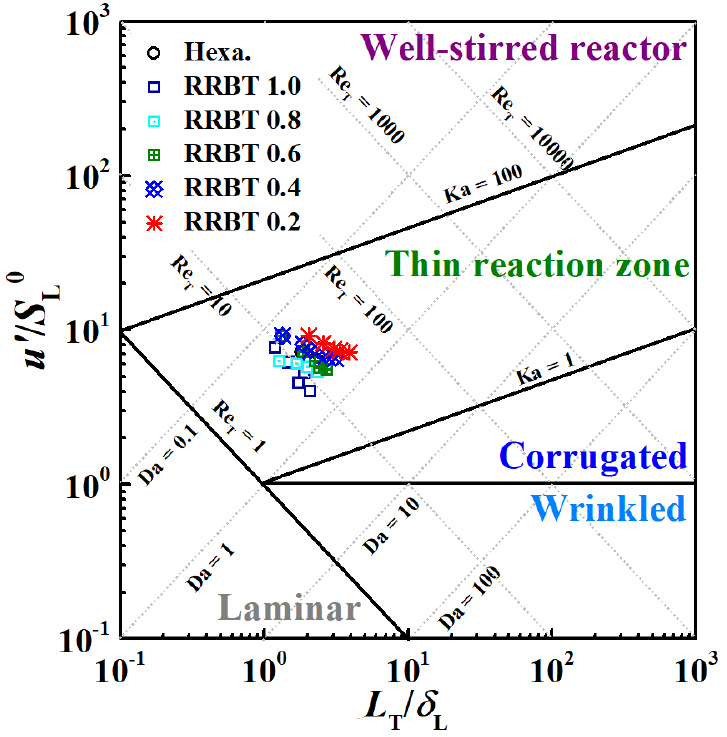
예혼합화염의 영역을 구분 지어주는 Borghi - peter 선도는 난류변동성분()과 층류연소속도()의 비와 적분 길이스케일()과 층류화염두께()의 비로 표현되며, 예혼합화염의 구조적 특성을 설명하는 것에 사용된다[28]. Borghi - peter 선도의 영역을 결정 짓는 유동성분은 LDV를 이용하여 화염기저(flame base) 전단에서의 정보를 취득하였다. 층류연소속도()를 계산하기 위해 PREMIX 코드[29]를 이용하여 계산하였으며, 층류화염두께()는 EQUIL 코드[30]를 이용하여 계산된 열확산도()를 사용하여 구하였으며 사용된 상세 반응 메커니즘은 GRI 3.0을 이용하였다[31]. 위 계산값을 이용하여 선도에 표현된 난류 Reynolds 수, ReT, Damkhöler 수, DaT, 그리고 Karlovitz 수, KaT는 식 (4)에 나타내었다[32, 33, 34].
본 연구에서 조사된 모든 격자의 경우 Fig. 7에서 보이는 바와 같이 10 < ReT < 100, 0.1 < DaT < 1, 1 < KaT < 100의 얇은 반응 영역(thin reaction zone)에 위치하는 것을 확인할 수 있었다. 해당 영역에서는 콜모그로브 길이스케일이 여전히 화염의 두께보다 크므로 직접적으로 침투하여 화염의 구조를 변경시키지는 못하지만, 예열대에 영향을 주어 난류 열 및 질량 확산도를 증진시킨다[28]. 결과적으로 전체 화염의 두께(flame brush)는 두터워지게 된다. 유동의 길이 스케일이 예열대(preheat zone)에 영향을 주기 시작하는 영역에서 프랙탈 형상의 격자가 만들어내는 하나의 흥미로운 점은 화염의 물성값들을 정규화하였음에도 RRBT가 줄어듦에 따라서 화염 영역의 위치는 조금씩 우측, 상단으로 증가하는 것이다. 이는 앞서 비반응 유동장에서 발견되었던, 웨이크 상호작용 이론으로 설명된 낮아지는 RRBT에 따라 발달하는 난류강도가 화염으로 들어가는 상류 혼합기(mixture)에 영향을 미쳐 과 를 증가시킨 것으로 확인이 된다. 증가된 속도성분과 길이스케일은 앞서 설명된 무차원수에 적용이 되어 선도 내 움직임을 보인 것으로 이해된다. 이러한 결과를 통해, 화염이 존재하는 조건에서도 프랙탈 격자의 적용으로 증가된 난류강도는 앞서 소개된 로 표현되는 Damkhöler 모델 식을 기반으로 생각했을 때, 저선회 화염의 난류화염속도를 뚜렷하게 증가시킬 것으로 기대가 된다.
3.3 난류유동과 저선회 화염의 상관식
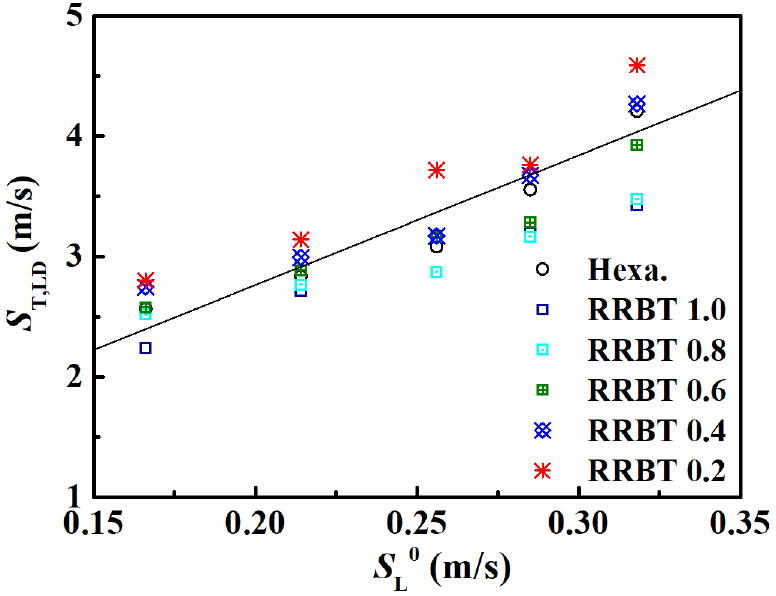
RRBT의 감소에 따라 증가된 난류강도에 영향을 받는 난류화염속도를 조사하기 전에 제안된 대부분의 모델 식 내부에 자리하고 있는 와 저선회 화염 전단에서 측정한 을 Fig. 8에 도시하였다. 모델 식에서도 보이듯이, 는 의 증가에 민감하게 반응하였고, 이론당량비( = 1)에 가까워 짐에 따라 증가하는 층류연소속도()는 실험적 연료 상수, 와 난류변동성분, 과 결합하여 난류화염속도를 선형적으로 증가시키는 것을 확인할 수 있다. 주목되는 부분은 격자에 따른 난류화염속도의 거동이 Fig. 5(b)에서 보여진 난류강도의 경향과 유사하게 분포하는 것을 볼 수 있는데, Hexa. 형상의 격자는 RRBT 0.4와 0.6 사이에서 존재하고, 프랙탈 형상의 격자들에서는 RRBT의 감소에 따라 난류 연소속도가 증가하는 것을 볼 수 있다. RRBT의 감소에 따라 높은 난류화염속도를 가지는 것으로 보아, 화염 전단의 유동장에 추가적인 난류에너지를 전달하여 난류연소속도를 증가시키는 것으로 이해가 된다. 상세하게 보자면, 화염이 존재하는 유동에서 기존의 Hexa. 형상의 격자를 기준으로, 난류 성능의 증대 효과가 가장 큰 RRBT 0.2의 는 모든 층류연소속도 조건에서 평균 10%의 상승을 보였고, 가장 저조한 난류강도를 보여주는 RRBT 1.0의 경우 다시 10% 감소하는 현상을 보였다.
화염이 존재하지 않은 유동장에서 RRBT의 감소는 다양한 유동스케일 간의 혼합 거리를 증가시켜, 난류 성능을 증가시키는 것을 난류강도의 거동과 에너지 스펙트럼을 통해 이전 절에서 확인하였다. 이와 마찬가지로, 프랙탈 형상이 유발한 난류 성능 증대 효과가 LDV를 이용하여 측정한 화염선단 기저 부분의 유동장에서도 동일하게 영향을 미치는 것이 확인되었고 RRBT의 감소는 화염의 유무에 상관없이 와 의 증가를 유도하며, 난류에너지()의 증가가 다양한 층류연소속도 조건에서도 적용되어 높은 난류화염속도가 형성되는 것을 관찰하였다.
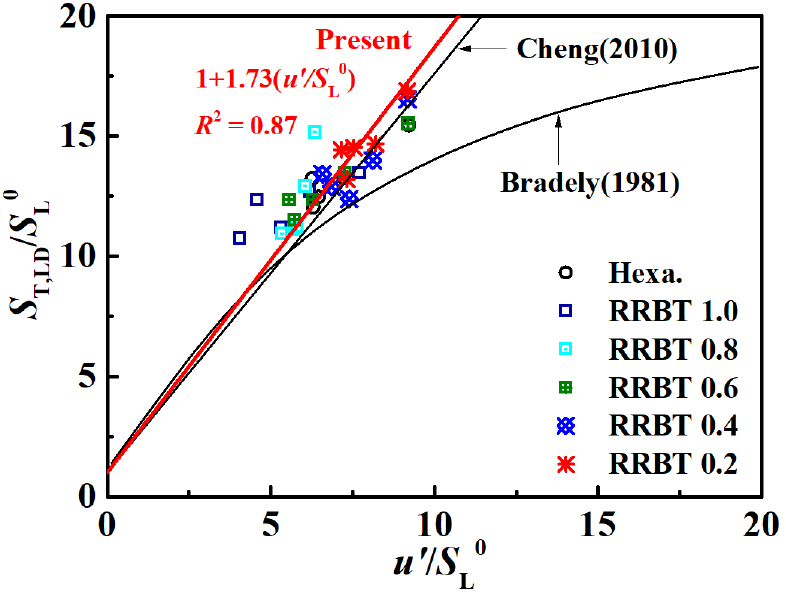
부상된 화염의 기저 부분에서 LDV를 통해 측정된 국부 변위 난류화염속도(local displacement turbulent flame speed, )는 정지된 화염 면에 수직으로 들어오는 반응물들의 유속으로 정의될 수 있다. 측정된 와 는 R.K. Cheng 등이 보고한 정규화된 화염속도 관계를 통해서 기존 연구와 비교할 수 있다[25]. Cheng은 연소기 내부 난류 생성 슬롯에서 발생하는 15 mm로 고정된 적분 길이스케일 기준 아래 < 30 조건까지의 과 의 관계를 식 (5)와 같은 선형적인 상관식으로 표현하였다[12, 25]. 제안된 식에서 는 연료의 실험 상수로 제안되었으며, 다양한 압력과 입구온도 조건에서 탄화수소(hydrocarbon) 연료인 경우 1.7 ~ 2.2, 수소(H2) 연료에서는 3.15 ~ 4.6으로 제안되었다[25, 26, 27, 35]. 하지만 연소기 내부 형상으로 인해 하나의 값으로만 고정되어 발생하기에 난류화염 면에 직접적인 영향을 미치는 화염 위치에서의 다양한 난류 스케일에 대한 상관관계를 파악하기에는 어려움이 있을 것으로 판단되었다. 따라서 본 연구에서는 고정된 유속 조건( = 10 m/s)에서 프랙탈 형상의 격자를 통해서 생성된 다양한 난류 유동스케일과 화염스케일 간의 상관관계를 파악하고자 한다. 이를 위해서 먼저 속도성분분인 과 국부 변위 평균 난류화염속도인 를 층류연소속도()로 각각 정규화한 과 의 비교를 Fig. 9에 나타내었다.
프랙탈 형상의 격자에서 RRBT의 감소는 난류강도를 증가시켜 난류화염속도가 증가되는 것을 이미 Fig. 8을 통해 확인되었다. Fig. 9에서 보이는 로 정규화된 은 < 10 범위에서 RRBT값이 작아짐에 따라 실험적 연료 상수 = 1.73(R2 = 0.87) 값을 가지며 선형적으로 증가하는 것을 볼 수 있다. 위와 같은 결과는 기존에 Cheng이 보고한 과 의 선형 관계(linear relationship)를 추종하는 것으로 확인이 되었다. 이것의 의미는 다양한 당량비 조건에 따라 발생하는 층류연소속도를 정규화(normalization)하였음에도 에 의해 발생한 의 상승은 프랙탈 형상의 격자가 현저히 증폭된 난류강도와 난류에너지를 통해 화염 면적의 확장을 유도하기 때문에 발생한 것으로 판단된다. 하지만, 기존 Cheng에서 보여준 식 (5)의 n = 1인 선형적인 결과와 달리 난류 구형 전파화염에서 Bradely가 제안한 의 증가에 n < 1 일때 나타나는 굽힘현상(bending effect)은 저선회 화염에서 발견되지 않았다[28]. 본 연구에서도 관찰되었듯이 에 1차 선형적인 의 관계는 저선회 화염의 연구 결과에서만 발견되는 현상이지만, 놀랍게도 그 이유에 대해서 아직까지 완전하게 밝혀지지 않았다. 이와 같은 현상을 분명히 이해하기 위해서, 얇은 반응영역의 난류 예혼합화염에 영향 미치는 인자에 속도변동섭동과 층류화염속도의 변수만 고려하는 것이 아니라, 유동과 화염의 길이스케일이 포함된 상관관계를 제안하는 것이 난류화염속도가 가지는 선형적 거동의 원인을 명확히 설명할 수 있을 것으로 판단된다.
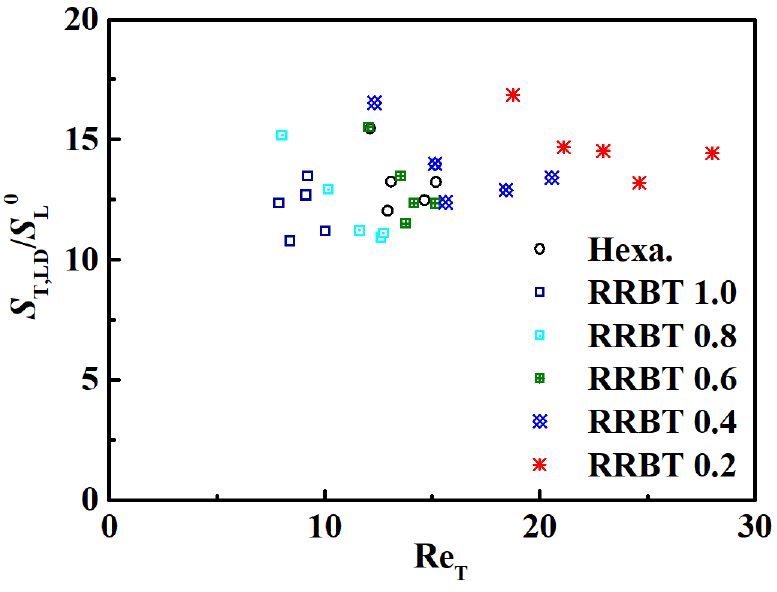
Fig. 10은 층류연소속도로 정규화된 국부 변위 난류화염속도를 유동 내의 에디의 성분() 과 층류 화염에 근거한 정보()의 비를 의미하는 난류 Reynolds 수인 ReT를 Hexa. 형상과 프랙탈 형상의 격자에 대하여 도시한 것이다. 유동과 화염의 성분으로 무차원화된 난류 Reynolds 수, ReT의 정의를 생각해보면, ReT는 에 비례항으로 작용한다. 따라서 이 0으로 수렴하게 되면, ReT도 0으로 줄어들게 되어, 난류화염속도와 층류화염속도는 동일한 값()을 가지게 된다. 따라서 ReT의 증가에 따라 의 값은 ReT0.5 형태를 만들어내며 증가하는 특징을 보이며, 적분 길이스케일의 효과는 제곱근에 비례하는 것으로 나타났다. 위와 같은 거동은 이전의 난류 예혼합화염들의 연구인 구형 전파 화염과 V 형태의 화염에서 측정된 결과와 유사한 경향을 보였다[28, 32, 36]. 앞서 설명된 난류변동성분과 난류화염속도의 간단한 1차 선형 관계와 달리 제곱근 형태로 거동한다는 의미는 얇은 반응 영역(thin reaction zone)의 난류화염속도에 영향을 미치는 인자를 고려함에 유동 및 화염의 스케일이 포함되어야 한다는 것을 의미한다. 다른 한편으로는 Fig. 9에서 보여진 다양한 격자에 대하여 중첩된 현상들과 달리 Hexa. 형식과 프랙탈 격자들은 RRBT 별로 ReT의 증가에 따라 분명하게 구분되어 영역을 형성하는 것을 확인할 수 있다. 실험된 당량비 조건에서 Hexa. 형상의 경우 앞서 비(非)반응장에서 보였듯이 RRBT 0.4와 0.6의 ReT 사이에 위치하는 것을 불 수 있고, 난류 성능 효과가 가장 컸었던 RRBT 0.2는 ReT = 35 ~ 56의 범위에서 가장 높게 분포한다. 즉, RRBT의 감소에 따라 ReT값은 약간의 영역을 공유하며 순차적으로 증가하는 것을 알 수 있다. 이러한 현상의 의미는 층류화염두께()와 유동의 적분 길이스케일()이 배제된 난류화염속도와 만의 상관관계와 달리, 당량비에 따라서 화염과 유동의 길이스케일을 포함한 ReT은 당량비 조건에 의존하는 층류화염의 고유성분과 예열대 내부에서 확산도를 증가시키는 난류유동성분의 효과를 반영해 주고 있기 때문으로 판단된다. 따라서 얇은 반응 영역대에 존재하는 화염 조건 내에서 프랙탈 형상의 격자가 만들어내는 다양한 유동 길이스케일의 영향이 분명하게 확인되었으므로, 유동과 화염의 길이스케일을 포함하여 난류화염속도를 평가하는 것이 속도성분만을 이용하는 것보다 화염 간의 상관관계를 더욱 면밀하게 분류할 수 있는 것으로 해석할 수 있다. 그렇지만 추가적으로 이러한 상관관계에서 각각의 내부 인자에 대한 영향을 분리하여 해석하기 위해서는 앞서 소개된 과 난류의 길이스케일과의 함수 결합을 통한 상관식 제시를 기반으로 이해하여야 한다.
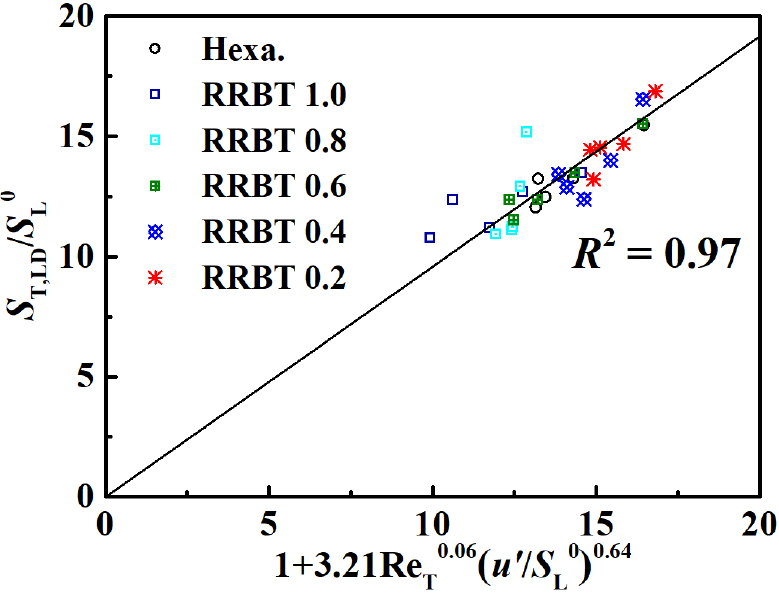
유동과 화염의 길이스케일을 내포한 ReT와 이 결합된 상관관계식을 정규화된 난류 평균 속도와의 관계로 Fig. 11에 도시하였다. 그 결과 다양한 RRBT값의 프랙탈 형상과 Hexa. 형식의 격자에서 발생하는 모든 무차원화된 난류 평균 화염속도는 식 (6)에 대하여 높은 결정 계수(R2 = 0.97)를 가진 선형적인 결과를 보였다. 여기서 주의 깊게 관찰해야 할 부분은 상관식을 구성하고 있는 변수 ReT와 이다. ReT의 정의를 생각해보았을 때, 0.06의 지수 값을 작용하고 있는 부분은 유동과 화염의 길이스케일 비에 해당하는 부분이고, 에 관하여 무시할 만큼 소극적으로 작용하는 것을 알 수 있다. 반면에 은 0.64의 지수 값과 함께 전체적으로 선형적인 함수 형태를 결정하는 중요한 변수로 역할을 하고 있음을 볼 수 있다. 이러한 결과는 얇은 반응 영역(thin reaction zone)에서 Hexa. 형태와 프랙탈 형태의 격자가 만들어내는 다양한 유동 성분과 길이스케일을 가진 난류화염의 화염속도 값은 층류화염속도로 무차원화된 난류변동성분에 대단히 지배적으로 작용하는 것으로 이해할 수 있다. 또한 상관식 선 상에서 RRBT에 따른 난류화염속도의 위치를 살펴보면 같은 상관식 값을 가졌음에도 불구하고 RRBT 별 의 분포는 매우 다양하게 발생하고, 이것은 유동스케일과 속도성분 외 난류화염에 영향을 미치는 다른 인자가 존재하는 것을 의미한다.
지금까지 보여준 관계식들은 난류유동의 길이스케일과 속도성분만의 상관관계를 보여주었다. 앞서 보여진 결과를 통해 관계식에 사용된 인자들만으로는 얇은 반응 영역에서 발생하는 구조적 특징과 유동에 대한 응답들을 완전히 설명할 수는 없다. 즉, 프랙탈 형상으로부터 발현된 난류 성능 또는 화염 신장이 유발하는 추가적인 열 및 물질 확산도와 다양한 연료 혼합 조건에 따라 상이한 확산도를 비교함으로써 분자 수준에서의 열 및 물질 전달 과정이 난류화염면에 작용하는 역할을 더욱 섬세하게 이해할 수 있다고 판단된다.
4. 결 론
저선회 연소기의 확대유동을 형성하는데 핵심적인 역할을 하는 중앙 난류생성판의 형상을 기존 일반 타공형 Hexa. 격자와 십자(十字) 형태의 프랙탈 격자를 적용하였을 때 발생하는 다양한 난류 속도성분과 길이 성분에 대한 부상 화염과의 상관관계를 조사하여 다음과 같은 결론을 도출했다.
1) 난류평균속도는 난류생성판 이후 급격하게 감소하는 현상을 보이며, Hexa.와 프랙탈형상의 RRBT 1.0 ~ 0.8은 지속적인 감소를, RRBT 0.6 ~ 0.2는 최저점 이후 약간 증가하는 형상을 보였다. 노즐 출구 이후 모든 격자에서 난류평균속도는 근소한 차이의 속도 확대율(ax)을 보였으며, 가상원점(Zo)과 노즐 출구위치(ZE)의 보상에서도, 모든 격자에서 저선회 화염의 안정화 메커니즘인 자기 상사성(self similarity)의 특성이 잘 나타나므로 넓은 유속 범위에서도 일정한 부상높이를 유지할 것으로 판단된다.
2) 축 방향으로 조사된 완화길이 이전 영역에서 프랙탈 격자의 최대 난류강도값과 난류변동성분의 최대 위치와 일치하였으며 RRBT가 줄어듦에 따라 두 값이 발생하는 위치가 후류로 밀려나는 현상이 웨이크 상호작용 이론으로 설명되었다. 또한 RRBT 감소에 따라 증가된 난류강도는 부상화염이 위치하게 되는 Z = 1.7 ~ 2.1D에서 높은 난류에너지가 공급되는 것을 에너지 스펙트럼을 통해 확인하였다.
3) 본 연구에서 이용된 화염은 모두 얇은 반응 영역(thin reaction zone)에 위치하는 것을 Borghi – Peter 선도를 통해 확인하였다. 선도 분석을 통해 RRBT의 감소에 따라서 선도 내의 우측 상단 방향으로 이동하는 것을 관찰하였고, 격자에 의해 발달된 난류에너지가 화염으로 들어가는 난류 유동에 영향을 미쳐 난류 적분 스케일()과 변동성분()을 증가시킨 것으로 이해되었다.
4) 프랙탈 형상의 격자를 통해서 생성된 다양한 난류스케일과 화염스케일 간의 상관관계를 파악하기 위해, RRBT 별 당량비 조건에 따른 과 를 비교하였다. RRBT의 감소는 정규화된 유동 및 화염 성분에서 1차 선형 증가하는 거동을 만들어냈고, 프랙탈 격자가 현저히 증폭된 을 형성하여 발생한 것으로 판단하였다. 이와 같은 현상은 기존에 Cheng이 보고한 저선회 연소기에서의 에 따른 거동과 유사하였다.
5) 길이스케일과 속도성분의 비로 이루어진 난류 Reynolds 수인 ReT는 와 제곱근으로 비례하는 관계를 보여주어 길이스케일의 영향이 비(非) 선형적인 거동을 유도한다는 것을 보여주었다. 추가적으로 난류 길이스케일과 속도성분 인자들의 영향성을 파악하기 위해 상관식을 제시하였다. 선형적으로 엮어진 상관식과 의 관계에서 길이스케일을 내포한 난류 Reynolds 수인 ReT보다 속도성분만을 의미하는 의 영향이 크게 작용하였고, 이는 속도성분이 유동과 난류화염속도의 전체적인 상관관계 형태를 만들어내는 주요 인자가 됨을 보였다.
기호설명
: Swirl number for low swirl injector
: Bulk velocity
: Axial mean velocity
: Axial velocity fluctuation
: Turbulent intensity
: Equivalence ratio
: Laminar flame thickness
: Integral length scale
: Laminar burning velocity
: Local displacements turbulent flame speed
ReT : Turbulent Reynolds number