Digital Twin for Prediction of the Steady State Temperature Field of a Natural Gas Boiler

Jinwoo Park; Woojin Lee; Sungbum Kim; Kang Yul Huh

doi:10.15231/jksc.2021.26.2.001

Preview

Research Article

Journal of The Korean Society Combustion. 30 June 2021. 1-13
https://doi.org/10.15231/jksc.2021.26.2.001

Digital Twin for Prediction of the Steady State Temperature Field of a Natural Gas Boiler

천연가스 보일러 내부 정상상태 온도장 예측을 위한 디지털 트윈 구축에 대한 연구

Jinwoo Park¹

Woojin Lee¹

Sungbum Kim¹

Kang Yul Huh¹^*

박 진우¹

이 우진¹

김 성범¹

허 강열¹^*

¹Department of Mechanical Engineering, Pohang University of Science and Technology

¹포항공과대학교 기계공학과

^{*Corresponding Author}

ABSTRACT

In this study, a simulation-based digital twin is developed for large-scale industrial natural gas boiler. The digital twin can predict temperature distribution under unexplored operating conditions by a regression model and a limited number of sensor data. The former is generally known as a surrogate model and the latter is known as sparse reconstruction. Proper orthogonal decomposition method is employed together with a kriging regression model for the surrogate model and gappy proper orthogonal decomposition for sparse reconstruction. Three-dimensional simulation data of the natural gas boiler are collected in the parameter space, which consists of excess air rate and swirl vane angle of the device. The surrogate model provides prediction performance within 5% least squared error. With sparse reconstruction, more than 32 measuring points provides prediction performance within 10% least squared error. The results show that the proper orthogonal decomposition has high potential as an analysis method for digital twin and prediction of reacting scalars in industrial combustion devices.

Keywords

Digital twin

Gappy POD

Natural gas boiler

POD

MAIN

1. 서 론
2. POD와 센서 배치 최적화
2.1 POD
2.2 Gappy POD
3. 수치 해석
3.1 모델 연소기
3.2 수치 해석
3.3 POD-Kriging 및 Gappy POD 설정
4. 결 과
4.1 POD 모드 분석
4.2 POD-Kriging 성능 분석
4.3 Gappy POD 성능 분석
4.4 예측 결과 분석
5. 결 론

1. 서 론

천연가스발전은 석탄화력발전과 친환경발전의 대안으로서 주목되고 있는 발전방식이다. 천연가스발전은 심화되고 있는 온실가스 및 유해 물질 저감 요구에 석탄화력발전을 과도기적으로 대체하는 방식으로 비중을 늘려가고 있으며, 2020년 6월 기준 OECD 가입국에서 생산한 에너지원의 30.2%의 비중을 차지하는 주요한 발전방식으로 정착되고 있다[1]. 천연가스 보일러가 석탄 화력 보일러 대비 적은 환경적 부담을 주지만, 연소로 내의 고온 영역으로 인해 발생하는 thermal NOx의 저감은 여전히 해결이 필요한 과제로 남아있다. 이를 배경으로, 천연가스 보일러에서 보일러 내부 고온 영역을 최소화하는 운전조건 연구는 thermal NOx의 저감을 위한 환경적, 경제적 의미가 있다.

천연가스 보일러와 같은 대형 연소기의 내부 온도장 예측 방법으로 전산 유체 해석(computational fluid dynamics, CFD)이 전통적으로 활용되고 있다. 그러나, 대형 물리공간을 다루기 위해 소모되는 막대한 전산량은 CFD의 한계점으로 인식된다. 이러한 한계점을 극복하고자 디지털 트윈에 대한 필요성이 대두되고 있으며, 산업 전반에 적용하고 있다. 디지털 트윈은 실제 시스템의 가상 모델로서, 공정 시스템 모델 등에는 머신러닝(machine learning) 알고리즘을 이용해 적용되어 왔으나[2] 산업용 연소기의 CFD에는 데이터의 양이 방대하여 적용이 쉽지 않다. 최근에는 Aversano et al. 에 의해 반응 유동[3] 및 연소기[4]에 대한 연구가 발표되었으나, 아직 실용 연소기 및 반응 유동의 디지털 트윈에 대한 연구는 부족한 실정이다.

다양한 물리량이 상호 영향을 미치는 대형 연소기 내부를 예측하기 위한 새로운 방법으로서 차수감축법(reduced order method, ROM)은 효율적인 대안이 될 수 있다. ROM은 고차원의 데이터를 차원 축소 변환시켜, 데이터 처리에 소모되는 시간을 크게 단축하는 방법이다. ROM은 머신러닝, 적합직교분해(proper orthogonal decomposition, POD) 등 데이터의 주요 정보를 유지하며 차원을 줄이는 다양한 방법을 포괄한다. 대형 연소기의 3차원 CFD에는 많은 데이터를 포함하는 디지털 트윈을 구축하기 위해 POD 기법이 널리 적용되고 있다.

Karhunen-Loeve expansion을 기반으로 하는 벡터 복원 기술인 POD는 이미지 복원[5], 패턴 인식[6], 그리고 멀티스케일 유체 유동[7], [8], [9]에 적용되고 있다. POD는 고차원의 full order space를 저차원의 orthogonal subspace에 투영하여, 시스템이 포함하는 주요 정보를 유지하며 차수를 효과적으로 줄이는 방식으로 작동한다. 구체적으로, POD는 시스템의 주요 특성을 반영하는 저차원의 POD mode들을 추출하며, 이렇게 추출된 POD mode들과 modal coefficient들을 결합하여 벡터를 복원한다[10].

POD에서 modal coefficient 예측은 필수적인 과정이다. 크리깅(kriging)은 파라미터 공간에 분포하는 스냅샷(snapshot)들을 통해 전체 파라미터 공간에서의 추세적인 modal coefficient 패턴을 얻은 후, 임의 운전조건에서의 modal coefficient를 예측하는 기법이다. 크리깅은 물리적 센서의 측정값에 의존할 필요 없이 확보된 스냅샷만으로 임의 운전조건에서의 스칼라 유동장을 확보할 수 있는 장점을 가지고 있다. Aversano et al.[4]은 MILD(moderate or intense low-oxygen dilution) 연소기를 대상으로 POD와 크리깅 모델(POD-Kriging)을 활용한 디지털 트윈을 구축하여 10% 이내의 오차율로 스칼라 유동장을 예측했음을 보고하였는데, 이는 POD-Kriging이 산업용 연소기 분석에 활용 가치가 있음을 보여주는 연구사례이다. Modal coefficient 예측을 위하여 센서를 활용하는 방법으로 Everson and Sirovich[11]는 Gappy POD를 도입하였다. Gappy POD는 천이 유동 패턴 예측[12], [13], [14]에 활용되어 소수의 센서 데이터를 활용하여도 높은 예측 정확도를 기대할 수 있음을 확인한 연구사례들이 있다.

이 연구에서는 대형 천연가스 보일러에 대하여 POD- Kriging과 Gappy POD 기법을 적용한 디지털 트윈을 구축해 보았다. POD-Kriging을 적용한 디지털 트윈 구축을 통해서 2차원 운전조건 공간 내 그리드 개수에 따른 훈련오차(training error)와 예측오차(prediction error)의 추이를 분석하여 POD-Kriging의 성능을 확인하였다. Gappy POD를 적용한 디지털 트윈에는 Gappy POD의 실제 연소기로의 적용성을 검토하기 위하여 보일러 벽면에 센서들을 배치하여 스칼라 유동장 예측 성능을 평가해 보았다.

2. POD와 센서 배치 최적화

2.1 POD

POD를 정상상태 다중파라미터 응용사례에 적용하기 위해서 $m$ 개의 운전조건에 대응하는 학습용 데이터인 스냅샷이 필요하다. 압축성 유체의 난류 유동 전산 시뮬레이션에서 식 (1)과 같이 정의되는 Favre 평균은 격자 공간의 시간 평균 스칼라량을 기술하는 방법으로 널리 활용된다.

(1)

\tilde{ϕ} = \frac{\int ρ (t) ϕ (t) d t}{\int ρ (t) d t}

식 (1)에서 $ρ (t)$ 와 $ϕ (t)$ 는 각각 시간 $t$ 에서의 순간 밀도 및 스칼라량을 의미한다. 본 연구에서 스냅샷은 모든 가상공간의 Favre 평균 온도로 구성된 벡터가 고려되었다. 이에 따라, $k$ 번째 운전조건에 대응하는 정상상태 Favre 평균 온도장 벡터 ${\vec{\tilde{T}}}_{k}$ ( $\in ℝ^{n}$ )는 아래와 같이 표현되며, 이들 벡터를 $k$ 번째 스냅샷으로 지칭하기로 한다.

(2)

\vec{{\tilde{T}}_{k}} = {[\tilde{T} (x_{1}, k) \tilde{T} (x_{2}, k) \dots \tilde{T} (x_{n}, k)]}^{T} k = 1, 2, \dots, m

식 (2)에서 $x_{i}$ 는 3차원 공간상의 $i$ 번째 위치를 의미하며, $n$ 은 공간 지점의 총 개수이며 스냅샷 벡터의 크기를 의미한다.

$m$ 개의 스냅샷이 확보되면 스냅샷 행렬 X( $\in {\ℝ}^{n \times m}$ )가 식 (3)와 같이 구성될 수 있다.

(3)

X = [\begin{matrix} │ & │ & │ \\ \vec{{\tilde{T}}_{1}} & \vec{{\tilde{T}}_{2}} & \dots & \vec{{\tilde{T}}_{m}} \\ │ & │ & │ \end{matrix}]

특이값 분해(singular value decomposition, SVD)는 임의의 복잡 행렬을 직교행렬로 대각화 할 수 있는 방법으로서, POD에서는 스냅샷 행렬이 가지고 있는 정보를 서로 직교성을 가지는 POD mode들로 분해하는데 활용된다. X는 특이값 분해를 적용하면 식 (4)과 같은 형태로 분해된다.

(4)

X = U Σ V^{T}

식 (4)에서 U( $\in {\ℝ}^{n \times m}$ )는 POD mode ${\vec{ψ}}_{k}$ 로 구성된 행렬이며, 식 (5)와 같이 표현된다.

(5)

U = [\begin{matrix} │ & │ & │ \\ \vec{ψ_{1}} & \vec{ψ_{2}} & \dots & \vec{ψ_{m}} \\ │ & │ & │ \end{matrix}] \vec{ψ_{m}} \in ℝ^{n}

∑( $\in ℝ^{m \times m}$ )는 특이값, $\{σ_{1}, σ_{2}, \dots, σ_{m}\}$ ,들로 구성된 대각행렬이다. $σ_{k}$ 는 X에서 ${\vec{ψ}}_{k}$ 이 포함하고 있는 정보의 비중과 비례하며, $σ_{k}$ 의 상위 $k$ 번째까지의 누적 에너지 포획량(cumulative energy capture)을 식 (6)과 같이 산출할 수 있다.

(6)

E_{k} = \sum_{i = 1}^{k} \frac{σ_{i}}{(σ_{1} + σ_{2} + \dots + σ_{m})} \times 100 (%)

일반적으로, 계산의 효율성과 복원 정확성을 동시에 확보하기 위하여 누적 에너지 포획량이 특정 수준 이상을 만족하는 POD mode들만을 복원에 활용한다. 이에 따라, 스냅샷들이 가지는 대부분의 특성을 표현할 수 있는 l개의 POD mode들만으로 구성된 직교행렬 U_trunc.( $\in {\ℝ}^{n \times l}$ ) 를 식 (7)과 같이 구성할 수 있다.

(7)

U_{t r u n c .} = [\begin{matrix} │ & │ & │ \\ \vec{ψ_{1}} & \vec{ψ_{2}} & \dots & \vec{ψ_{m}} \\ │ & │ & │ \end{matrix}] l \leq m

식 (7)에서의 POD mode들은 임의 운전조건에서의 정상상태 온도장 벡터, ${\vec{\tilde{T}}}_{t r u n c .}$ ,를 식 (8)과 같이 복원하는 데 활용된다.

(8)

{\vec{\tilde{T}}}_{t r u n c .} = \sum_{i = 1}^{l} α_{i} \vec{ψ_{i}}

식 (8)의 modal coefficient, $α_{i}$ ,의 예측에는 본 연구에 적용된 바와 같이 크리깅[15] 등의 회귀모델(regression model)이 주로 활용되고 있다.

2.2 Gappy POD

Gappy POD는 센서 위치를 스냅샷의 3차원 공간으로 투영하는 마스크 벡터 $\vec{g}$ ( $\in {\{0, 1\}}^{n}$ )을 활용하며, $g_{i}$ 를 $\vec{g}$ 의 i 번째 요소라고 할 때 다음의 규칙을 가진다.

$g_{1} = 1$ (센서가 i번째 위치에 있는 경우)

$g_{1} = 0$ (센서가 i번째 위치에 없는 경우)

Gappy POD를 통해 복원된 완전한 정상상태 온도장 벡터를 $\vec{{\tilde{T}}_{g}}$ 라고 하면, $\vec{{\tilde{T}}_{g}}$ 는 식 (9)과 같이 표현할 수 있다.

(9)

\vec{{\tilde{T}}_{g}} = \sum_{i = 1}^{l} β_{i} \vec{ψ_{i}}

센서 측정을 통해 얻은 데이터들을 통해 구성된 불완전한 Favre 평균 온도장 벡터를 $\vec{{\tilde{T}}_{s}}$ 라고 하면 modal coefficient, $β_{i}$ ,는 식 (10)으로 표현되는 오차 최소화 문제의 해이다.

(10)

δ = {||{\vec{\tilde{T}}}_{s} - {\vec{\tilde{T}}}_{g}||}_{g}^{2}

식 (10)에서 $∥ ∥_{g}^{2}$ 는 Gappy norm이며[16], 식 (10)을 풀어서 정리하면 식 (11)의 형태를 얻을 수 있다.

(11)

δ = {||{\vec{\tilde{T}}}_{s}||}_{g}^{2} - 2 \sum_{i = 1}^{l} β_{i} ({\vec{\tilde{T}}}_{s}, {\vec{ψ}}_{i})_{g} + \sum_{i = 1}^{l} \sum_{j = 1}^{l} β_{i} β_{j} ({\vec{ψ}}_{i}, {\vec{ψ}}_{j})_{g}

식 (11)에서 $(\vec{u}, \vec{v})_{g}$ 는 Gappy 내적을 나타낸다[16]. 식 (11)을 $β_{i}$ 에 대해 미분하여 극점 조건을 부여하면 식 (12)와 같은 형태의 방정식이 된다.

(12)

\frac{\partial δ}{\partial β_{i}} = - 2 (\vec{\tilde{T}}, {\vec{ψ}}_{i})_{g} + 2 \sum_{j = 1}^{l} β_{j} ({\vec{ψ}}_{j}, {\vec{ψ}}_{i})_{g} = 0

식 (12)는 식 (13)과 같은 선형방정식의 형태로 정리될 수 있으며, $β_{i}$ 는 이 선형방정식을 풀어 결정된다.

(13)

M \vec{β} = \vec{f}

식 (13)에서 M은 성분 $M_{i j} = {(\vec{ψ_{i}}, \vec{ψ_{j}})}_{g}$ 들로 구성된 행렬이며, $\vec{f}$ 는 성분 $f_{i} = ({\vec{\tilde{T}}}_{s}, \vec{ψ_{i}})_{g}$ 들로 구성된 벡터이다.

3. 수치 해석

3.1 모델 연소기

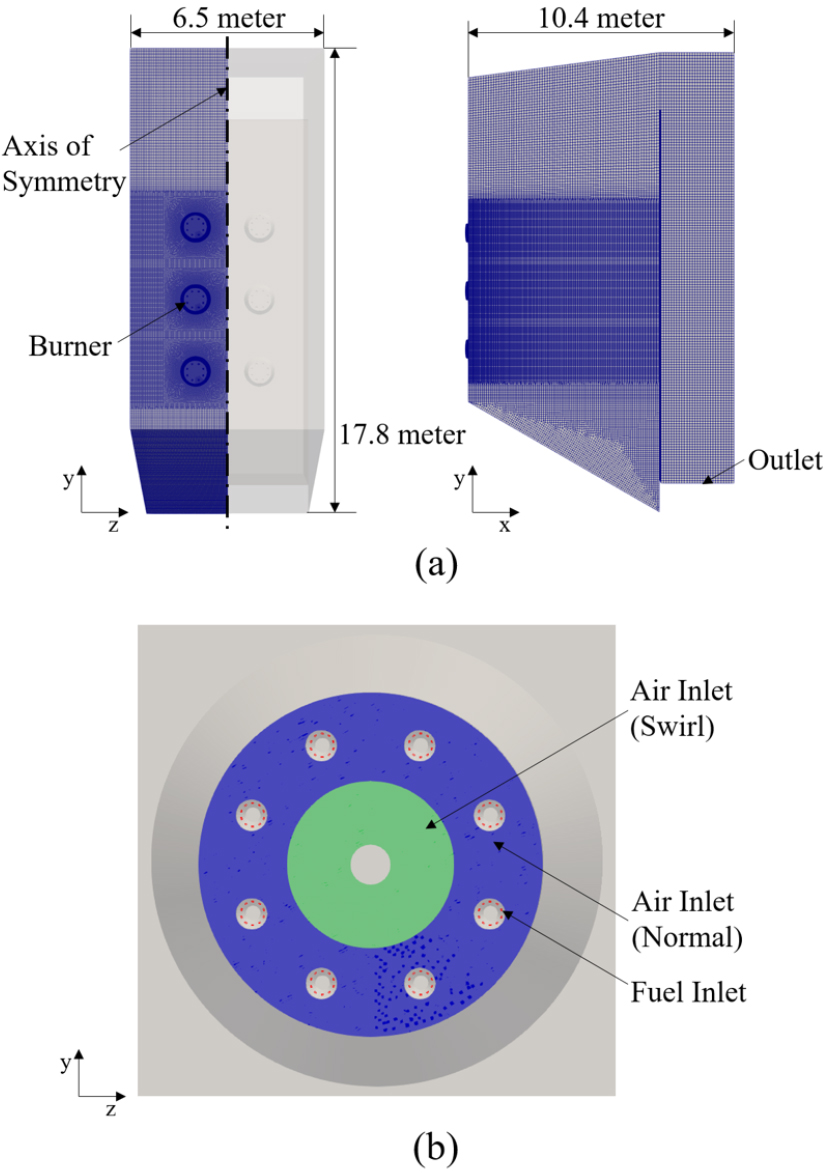
본 연구에서는 발전용 대형 천연가스 보일러의 다중파라미터 운전조건에 대한 전산 유체 시뮬레이션으로 얻어진 정상상태 Favre 평균 온도장을 POD-Kriging 및 Gappy POD 데이터 셋으로 활용하였다. Fig. 1은 전산 유체 시뮬레이션의 대상인 천연가스 보일러의 형상과 격자를 대략적으로 보여준다. 시뮬레이션 형상은 총 740만개의 격자로 구성되어 있으며, 계산의 효율성을 고려하여 대칭 구조 형상의 1/2 부분만을 시뮬레이션에 활용하고, y축 선상의 대칭면은 symmetry 경계조건을 부여하였다. 대상 보일러의 전면부에는 총 여섯 개의 버너 섹션이 있으며, 각 버너 섹션은 가운데에 swirl 공기 유입구와 바깥쪽 큰 반경을 따라 버너 면 기준 수직 방향으로 공기가 유입된다. 이와 같은 설계를 통해 바깥쪽 공기가 swirl 공기를 감싸며 화염을 부착시키게 된다. 연료는 수직 방향 공기 유입구를 따라 배치된 8개의 노즐에서 분사된다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F1.jpg

Fig. 1.

(a) Computational mesh of the target gas boiler and (b) its burner section.

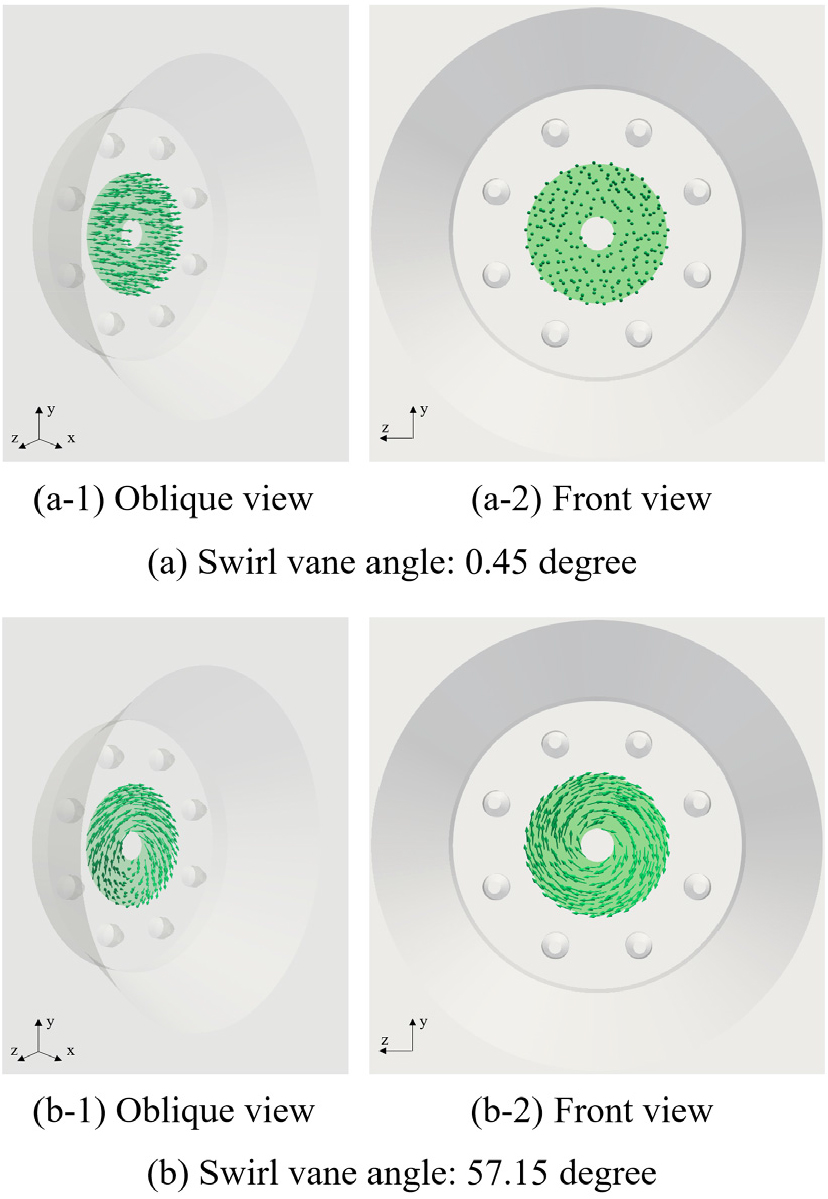
Table 1은 보일러의 운전조건이 요약된 표이다. 보일러의 연료는 100% 메탄(CH₄)으로 가정하였고, 산화제는 질량 기준 23.3%의 산소(O₂)와 76.7%의 질소(N₂)로 구성된 공기를 적용하였다. swirl 각도는 원형 버너 섹션의 접선 방향으로의 공기 유입 각도를 의미한다. swirl 각도에 따른 버너 입구에서의 공기 유입 방향은 Fig. 2에서 확인할 수 있다.

Table 1.

Burner operating conditions

Type	Parameter
Fuel flow rate	6,077 (kg/h)
Fuel temperature	293 (K)
Fuel composition	Methane (CH₄) 100%
Air flow rate	152,258 (m³/h)~182,710 (m³/h)
Air temperature	465 (K)
Swirl vane angle	0°~60° from normal dir.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F2.jpg

Fig. 2.

Directions of swirl inlet flows corresponding to two swirl vane angles: 0.45 degree and 57.15 degree.

3.2 수치 해석

모델 연소기에 대한 정상상태 수치해석은 오픈소스 전산 해석 코드인 OpenFOAM-4.x를 활용하였다. SIMPLE 알고리즘이 적용된 RANS(Reynolds averaged Navier- Stokes)를 통해 연속체 방정식과 모멘텀 전달 방정식을 다루었다.

(14)

\frac{\partial}{\partial x_{i}} (ρ {\tilde{u}}_{j}) = 0

(15)

\frac{\partial}{\partial x_{i}} (ρ {\tilde{u}}_{i} {\tilde{u}}_{j}) = - \frac{\partial p}{\partial x_{j}} + ρ g_{i} + (μ + μ_{t}) \frac{\partial^{2} {\tilde{u}}_{i}}{\partial x_{j}^{2}}

식 (14)에서 $\bar{ρ}$ 와 $u_{i}$ 는 각각 Reynolds 평균 밀도와 Favre 평균 속도의 $i$ 번째 성분을 의미하며, 식 (15)의 $p$ , g_i, 그리고 $μ_{t}$ 는 시간 평균 압력, 중력가속도 벡터의 $i$ 번째 성분, 그리고 난류점성계수(turbulence viscosity)를 의미한다. 이번 연구에서 활용한 난류모델은 realizable k-ε model[17]로, 식 (16)을 통해 난류점성계수를 예측한다.

(16)

μ_{t} = ρ C_{μ} \frac{{\tilde{k}}^{2}}{\tilde{ε}}

식 (16)에서 $C_{μ}$ (=0.09)는 모델 상수이며, $\tilde{k}$ 와 $\tilde{ε}$ 은 각각 Favre 평균 난류운동에너지(turbulent kinetic energy)와 난류소산율(turbulent kinetic energy dissipation rate)이다. 식 (17) 및 (18)는 위 난류모델에 적용된 $k$ 와 $\tilde{ε}$ 의 전달방정식이다.

(17)

\frac{\partial}{\partial x_{j}} (ρ {\tilde{u}}_{j} \tilde{k}) = (μ + \frac{μ_{t}}{σ_{k}}) \frac{\partial^{2} \tilde{k}}{\partial x_{j}^{2}} + P_{k} - ρ \tilde{ε}

(18)

\frac{\partial}{\partial x_{j}} (ρ {\tilde{u}}_{j} \tilde{ε}) = (μ + \frac{μ_{t}}{σ_{ε}}) \frac{\partial^{2} \tilde{ε}}{\partial x_{j}^{2}} + ρ C_{1} S \tilde{ε} - ρ C_{2} \frac{{\tilde{ε}}^{2}}{\tilde{k} + \sqrt{ν \tilde{ε}}} + S_{ε}

식 (17)에서 $σ_{k}$ (=1.0), $P_{k}$ 는 각각 $k$ 의 난류 Prandtl 수와 생성항을 의미한다. 식 (18)에서 $σ_{ε}$ (=1.2), $ν$ , 그리고 $S_{ε}$ 는 $\tilde{ε}$ 의 난류 Prandtl 수, 동점성계수(kinematic viscosity), 그리고 생성항이다. $S$ 는 평균 변형률(mean strain rate)을 의미한다. $C_{1}$ 은 식 (19)를 통해 결정된다.

(19)

C_{1} = \max [0.43, \frac{η}{η + 5}]

식 (19)에서 $η$ 은 식 (20)으로 계산되는 값이다.

(20)

η = S \frac{k}{ε}

$C_{2}$ (=1.9)는 모델 상수이다.

연소에 의한 Favre 평균 온도 계산은 확률밀도함수(probability density function, PDF)를 활용한 PDF 적분(PDF integration)으로 구하였다.

(21)

\tilde{T} = \int_{0}^{1} <\tilde{T} ξ = η> \tilde{P} (η) d η

식 (21)에서 $ε$ 와 $η$ 는 혼합 분율과 샘플 혼합 분율을 의미하며, $< \tilde{T} | \tilde{ξ} = η >$ 는 $η$ 와 같은 $ξ$ 값을 가지는 공간 내에서의 Favre 평균 온도를 의미한다. $η$ 에 대한 $< \tilde{T} |$ $\tilde{ξ} =$ $η >$ 의 분포를 의미하는 conditional profile은 GRI3.0 화학반응 메커니즘이 적용된 SLFM(steady laminar flamelet model)을 통해 구축하였다. $\tilde{P} (η)$ 는 PDF이며, 이번 연구에서는 베타분포를 가정하였다. 베타분포의 입력 변수인 Favre 평균 혼합분율(Favre mean mixture fraction, $\tilde{ξ}$ ) 및 Favre 평균 혼합 분율분산(Favre mean mixture fraction variance, $\tilde{ξ''^{2}}$ )의 공간상 분포의 계산에는 식 (22) 및 (23)의 전달방정식이 활용되었다.

(22)

\frac{\partial}{\partial x_{j}} (ρ {\tilde{u}}_{j} \tilde{ξ}) = \frac{μ_{t}}{S c_{t}} \frac{\partial^{2} \tilde{ξ}}{\partial x_{j}^{2}}

(23)

\frac{\partial}{\partial x_{j}} (ρ \tilde{u_{j}} \tilde{ξ^{'' 2}}) = \frac{μ_{t}}{S c_{t}} \frac{\partial^{2} \tilde{ξ^{'' 2}}}{\partial x_{j}^{2}} + \frac{2 μ_{t}}{S c_{t}} [{(\frac{\partial \tilde{ξ}}{\partial x_{i}})}^{2}] - 2 ρ \tilde{N}

식 (22)에서 $S c_{t}$ (=0.68)는 난류 Schmidt 수(turbulent Schmidt number)이고, 식 (23)의 $\tilde{N}$ 은 Favre 평균 스칼라 소산율(Favre mean scalar dissipation rate)이다.

3.3 POD-Kriging 및 Gappy POD 설정

Jin et al.[18] 에 의하면 저차원 파라미터 공간에 필요한 스냅샷의 개수는 식 (24)를 참고하여 결정할 수 있다.

(24)

(N u m b e r o f s n a p s h o t s) = 3 l \cdot (p + 1) \cdot (p + 2)

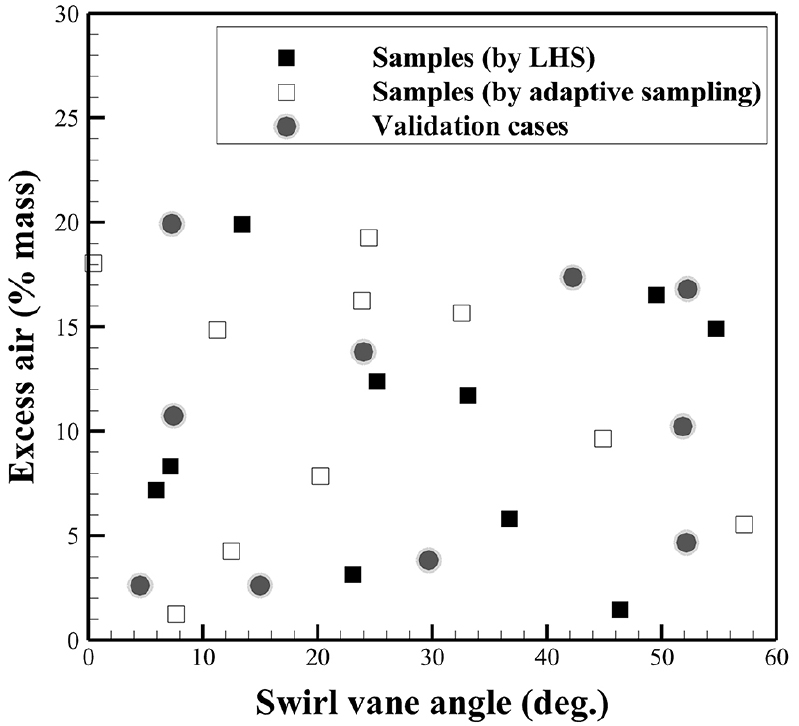
식 (24)에서 $l$ 은 모델 상수이며, 0.5 ~ 2 사이의 값을 가진다. $p$ 는 파라미터 공간의 차원 수이고, 본 연구에서는 2차원 파라미터 공간을 대상으로 Gappy POD가 적용되기에, 18 ~ 72개의 스냅샷이 권장된다. 본 연구에서는 보일러의 운전조건 중 swirl 각도(swirl vane angle)와 과잉 공기율(excess air)을 운전변수로 설정하였으며 두 운전변수로 구성한 2차원 파라미터 공간을 Fig. 3과 같이 구성하였다. 본 연구의 연료 및 산화제 조건에서 과잉 공기율에 따른 단열 화염 온도(adabatic flame temperature) 범위는 2,358.24 K (과잉공기율: 20%) ~ 2426.66 K(과잉공기율: 0%)이다. 식 (24)의 권장 스냅샷 개수를 바탕으로, 20개의 훈련용(snapshot) 운전조건과 10개의 검증용 운전조건을 결정하였다. 전체 스냅샷 중 latin hypercube sampling(LHS)으로 10개의 스냅샷 운전조건을 먼저 결정한 후, 나머지 10개의 스냅샷 운전조건은 adaptive sampling[19]을 적용하여 결정하였다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F3.jpg

Fig. 3.

Map of 20 samples and 10 validation cases in 2D parametric space.

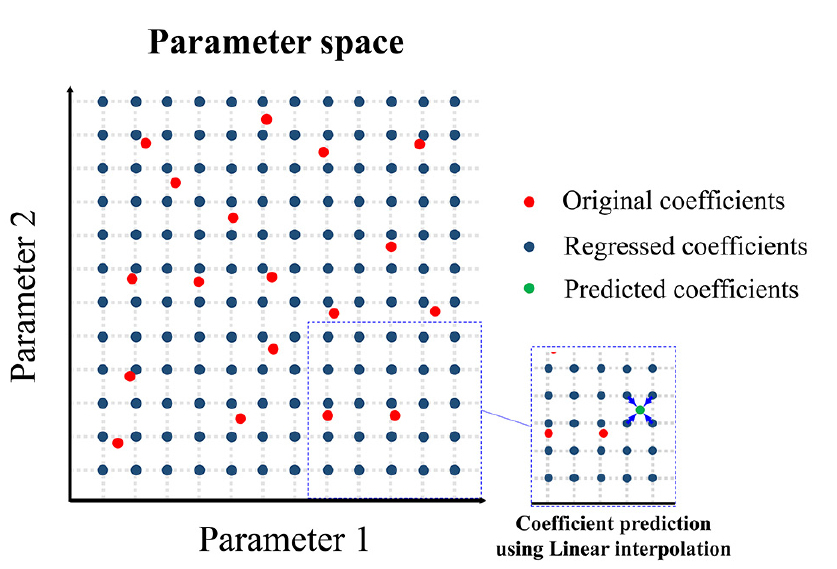
크리깅은 Fig. 4와 같이 특이값 분해로 계산된 modal coefficient를 바탕으로 파라미터 공간에 균등하게 분포된 각 그리드에 대응하는 modal coefficient(regressed coefficient)를 추출한다. 또한, 그리드에 대응하지 않는 부분에 대해서는 그리드에 해당하는 값으로부터 선형 보간(linear interpolation)을 이용하여 값을 추출한다. 따라서, 그리드의 개수와 분할 방식은 POD-Kriging의 예측 성능에 영향을 줄 수 있으며, 영향성 평가가 필요하다. 이에 따라, 이번 연구에서는 그리드 개수에 따른 훈련오차와 예측오차의 영향성을 평가하였다. 2차원 파라미터 공간의 각 축을 균등하게 나누었으며, $2^{n}$ 개(n = 1, 2, ... , 9)에 대한 그리드 분할이 영향 평가에 적용되었다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F4.jpg

Fig. 4.

Schematic diagram of coefficients prediction by Kriging.

또한, Gappy POD의 실제 연소기에서의 활용성을 고려하기 위해, 보일러의 모든 벽면을 센서 부착이 가능한 위치로 가정하였다. Gappy POD의 센서는 벽면이 아닌 각 POD mode들의 3차원 공간상 최대값 및 최소값을 나타내는 위치에 있을 때 높은 성능을 기대할 수 있는 것으로 알려지고 있다[13]. 그러나 실제 연소기 내부에 센서를 장착하여 데이터를 얻기는 어려울 수 있다.

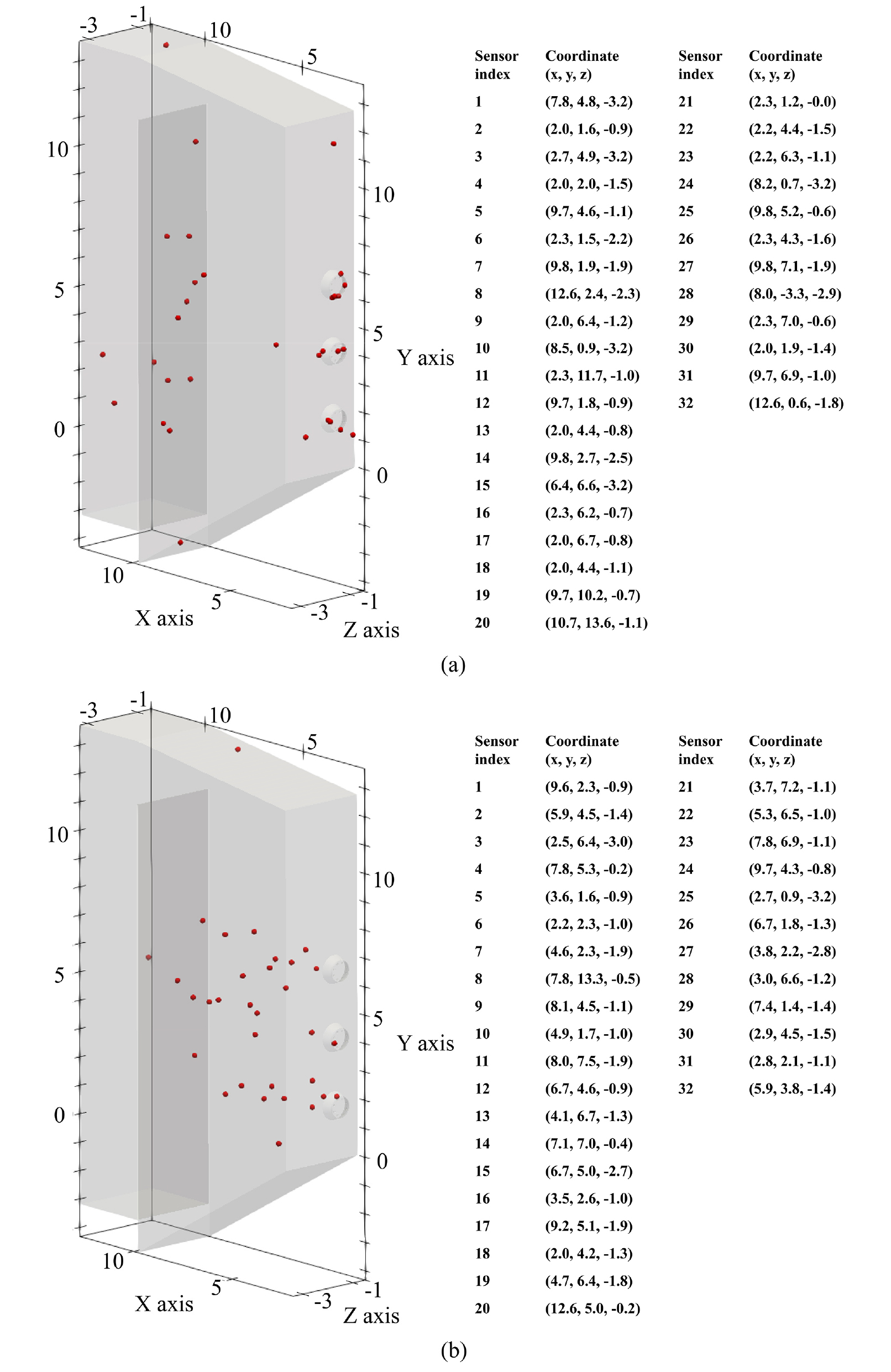
이번 연구에서는, 보일러 벽면에 부착된 센서를 활용한 Gappy POD 결과의 성능을 보일러 내부 배치된 센서를 활용한 Gappy POD 결과와 비교 검토하였다. Fig. 5는 이번 연구의 Gappy POD에 활용된 32개의 센서 위치를 보여준다. Fig. 5의 센서들은 시뮬레이션 형상을 구성하는 격자들의 인덱스를 대상으로 LHS를 적용하여 얻었다. 이에 따라 Fig. 5(b)와 같이 보일러 내부 배치 센서들은 격자의 밀도가 높은 화염 영역 주변에 집중되어 배치된 경향을 보이게 되었다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F5.jpg

Fig. 5.

Locations of the 32 sensors placed (a) on the wall and (b) in the domain.

4. 결 과

4.1 POD 모드 분석

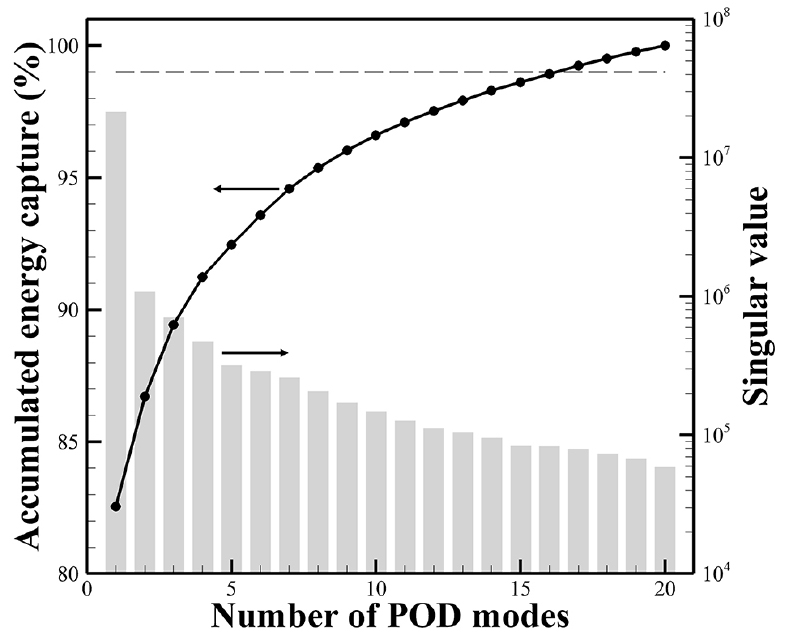
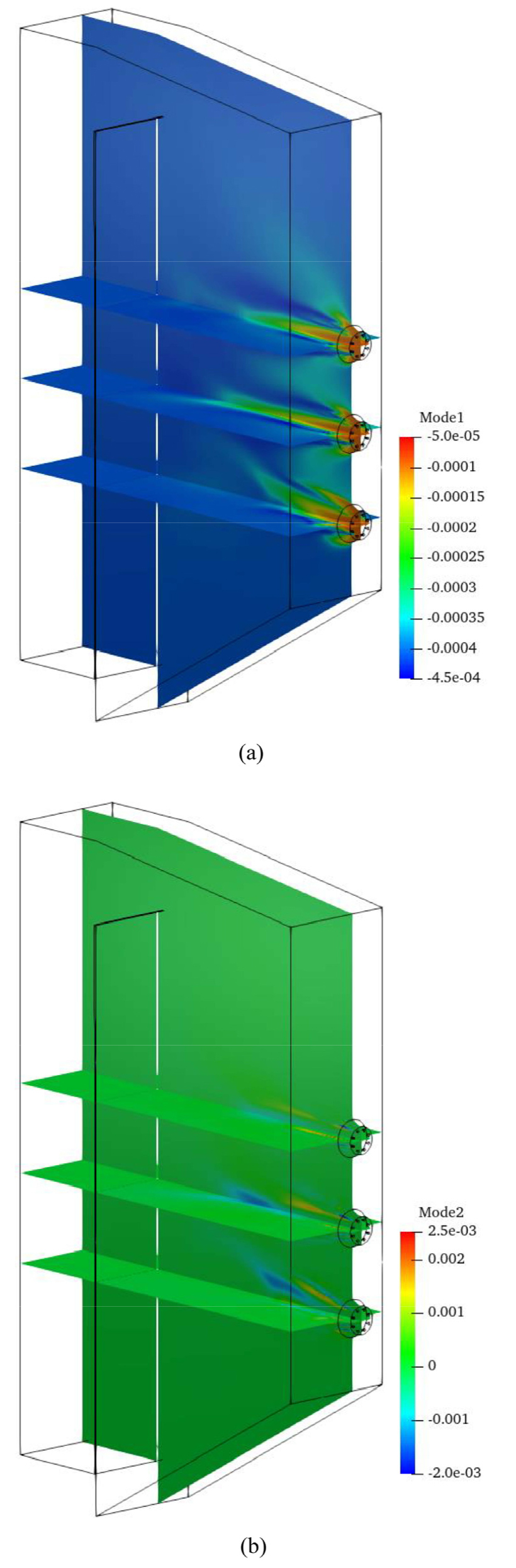
Fig. 6는 POD mode의 특이값 및 누적 에너지 포획량을 보여준다. 특이값 상위 19개의 POD mode가 전체 에너지의 99%를 포함하는 것을 확인하였고, 이 19개의 POD mode를 POD-Kriging 및 Gappy POD에 적용하여 스냅샷 및 검증케이스 복원에 활용하였다. Fig. 7은 복원에 활용된 19개의 POD mode들 중 특이값 기준 상위 두 모드인 mode 1과 mode 2이다. Mode 1은 전체 온도장 특성 중 특이값 기준 82%를 포함하고 있는 벡터로서, 스냅샷들의 Favre 평균 온도장의 대략적인 최소값 영역과 최대값 영역을 유사하게 모사하고 있다. Mode 2는 mode 1과는 다르게, 대부분 영역은 0에 가까운 중간값이며, 화염을 따라 국부적으로 최대값 영역과 최소값 영역이 분포되어있다. Fig. 7에 보여지지 않은 다른 mode들은 mode 2와 같이, 대부분 영역은 0이며 국부적인 최대값 영역과 최소값 영역이 있는 분포를 보인다. 복원에 있어 가장 큰 비중을 차지하는 mode 1에 의해 Favre 평균 온도 분포가 대략적으로 복원되고, 그 밖의 mode들에 의해 화염의 특징적인 형태가 세부적으로 복원되도록 구성된 POD mode 조합임이 확인된다. Mode 1의 값의 범위는 mode 2에서 나타나는 값의 범위와 비교하였을 때 전체적으로 크기가 작다. 이 점은 mode 1에 대응되는 특이값이 전체 특이값 중 가장 큰 점과 연계된 결과로 분석될 수 있다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F6.jpg

Fig. 6.

Singular values and cumulative energy captures for POD modes.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F7.jpg

Fig. 7.

Visualization of (a) mode 1 and (b) mode 2.

4.2 POD-Kriging 성능 분석

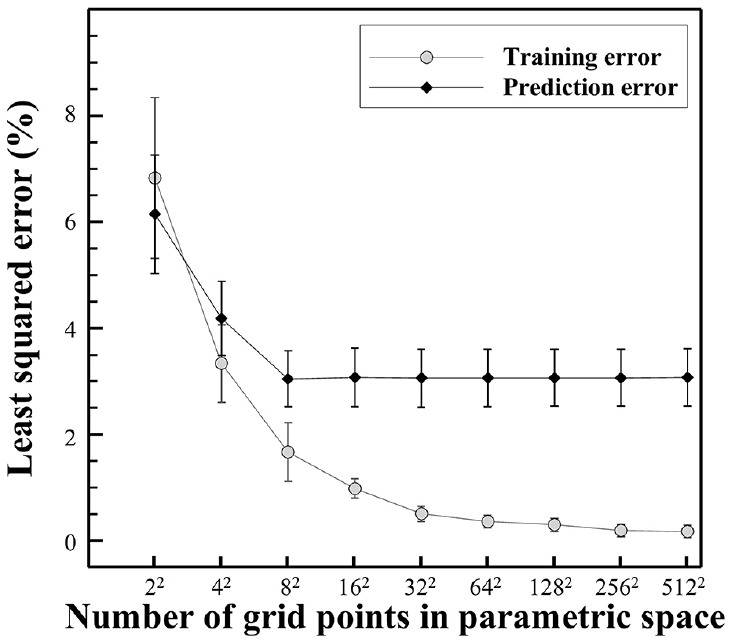
Fig. 8은 파라미터 공간 내 그리드 개수에 대한 POD- Kriging의 평균 훈련오차 및 평균 예측오차의 추이를 보여준다. 이번 연구에서의 평균 훈련오차는 예측된 20개 스냅샷의 원본 대비 평균 최소제곱오차(least squared error)를 의미하며, 평균 예측오차는 예측된 10개 검증용 케이스의 원본 대비 평균 최소제곱오차를 의미한다. 본 연구의 최소제곱오차의 산출에는 식 (25)가 적용되었다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F8.jpg

Fig. 8.

Mean least squared errors of POD-Kriging results versus number of grids in the parametric space and corresponding standard deviations. The standard deviations are indica- ted as error bars.

(25)

L e a s t s q u a r e d e r r o r = \sqrt{\frac{\sum_{i = 1}^{n} {(\tilde{T} (x_{i}) - {\tilde{T}}_{p r e d i c t} (x_{i}))}^{2}}{\sum_{i = 1}^{n} {(\tilde{T} (x_{i}))}^{2}}} \times 100 (%)

식 (25)에서 $\vec{\tilde{T}}$ 와 ${\vec{\tilde{T}}}_{p r e d i c t}$ 는 각각 시뮬레이션으로 얻은 원본 Favre 평균 온도분포와 POD-Kriging을 통해 예측된 온도분포를 의미한다.

POD-Kriging의 평균 훈련오차는 그리드 개수가 많을수록 점점 낮아지는 경향을 나타내었다. 파라미터 공간의 modal coeffcient 분포를 나타내는 반응 표면(response surface) 정보는 파라미터 공간상에 균등하게 배치된 각 그리드 지점에 대응하는 modal coeffcient 값들로부터 저장되고 복원된다. 이에 따라, 파라미터 공간상에 그리드 개수가 많으면 반응 표면 정보를 더 정교하게 저장하고 활용할 수 있다. Fig. 8에서 훈련오차의 추이는 그리드 개수가 많을수록 반응 표면이 정교하게 다루어짐을 보여주는 결과로 이해할 수 있다. 반면, 예측오차는 $8^{2}$ 개 이상의 그리드를 사용하는 경우 가장 낮은 수준이었으며, 이보다 많은 그리드를 사용하였을 때 과적합(overfitting)으로 인해 오차가 미세하게 증가함을 보여준다. 따라서, 이번 연구에서는 POD-Kriging을 위한 최적의 예측 성능이 $8^{2}$ 개의 그리드 개수를 적용하였을 경우 나타났다. $8^{2}$ 개의 그리드 개수로 복원된 Favre 평균 온도장은 CFD 시뮬레이션 결과 대비 약 3%의 평균 최소 제곱 오차를 보였으며, 검증데이터의 온도 데이터의 평균 절대량 오차는 22.52 K을 나타냈다.

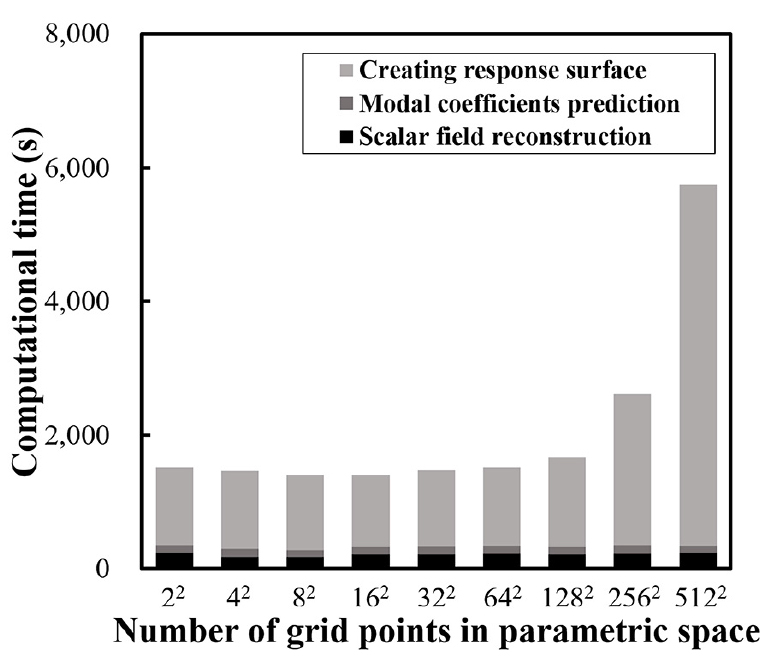
Fig. 9는 POD-Kriging을 이용하여 ROM을 구성하고 스칼라 필드를 예측할 때 소요되는 시간을 세 단계로 나누어 나타내었다. 128²개 이상의 그리드를 활용할 경우 그리드 개수에 따른 계산 시간(computational cost)이 비약적으로 증가하였으며, 전체 계산 시간 중에서 반응 표면 구성을 위한 계산 시간만이 그리드 개수에 따라 확연하게 증가하였다. 이미 구성된 반응 표면을 통한 modal coefficient 예측과 스칼라 필드 재구성을 위한 계산 비용은 증가하는 경향이 관찰되지 않았다. POD-Kriging을 위한 연산은 2.2 GHz의 동작속도를 가지는 Intel Xeon CPU E5-2630 v4를 활용하였다. 비교 가능한 계산 시간의 측정을 위하여 모든 계산은 하나의 코어만을 활용하였다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F9.jpg

Fig. 9.

Computational times of the predictions of the data sets of Favre mean temperature fields (comprised with 20 samples and 10 validation cases) by POD-Kriging.

4.3 Gappy POD 성능 분석

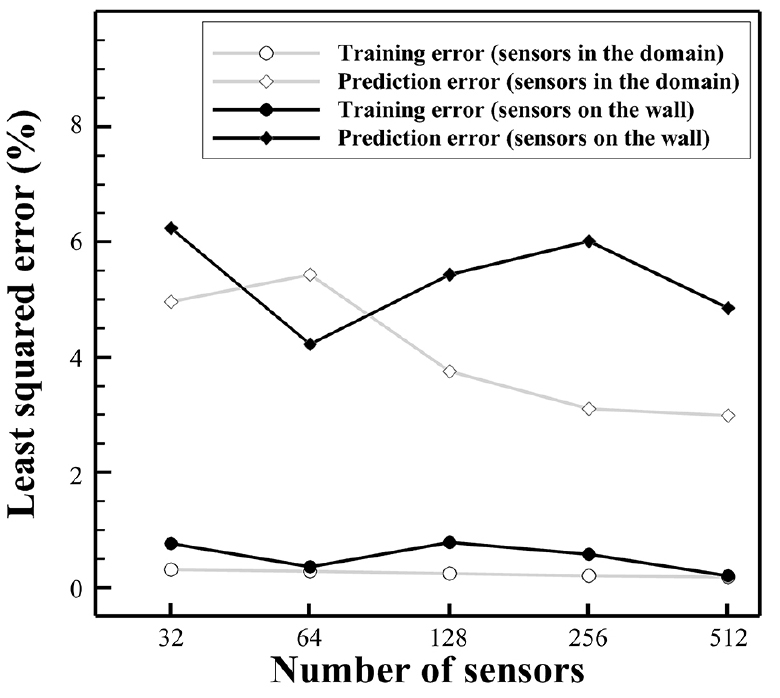
Fig. 10은 센서 개수에 따라 보일러 벽면 부착된 센서들(sensors on the wall)과 보일러 내부 배치된 센서들(sensors in the domain)로부터 얻은 각 Gappy POD 결과의 평균 훈련오차와 평균 예측오차 추이를 보여준다. Gappy POD 결과의 분석에도 POD-Kriging 결과 분석과 마찬가지로 식 (25)로 표현되는 최소제곱오차를 산출하였다. 32개 이상의 센서를 활용한 Gappy POD 결과는 7% 이내의 오차율을 보였으며, 32개 이상의 센서 개수의 증가에 따른 성능의 향상이 크지 않다는 점이 확인된다. Fig. 10에서 최소제곱오차가 가장 높은 수준을 보이는 데이터는 32개의 벽면 부착 센서를 활용하였을 때의 예측오차이며, 이 경우 6.23%의 최소제곱 오차 및 46.31 K의 평균 절대량 오차 수준이 나타난다. 보일러 벽면 부착된 센서들을 활용한 Gappy POD 결과들은 대체적으로 내부 배치된 센서를 활용한 결과들에 비해 높은 오차율을 보인다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F10.jpg

Fig. 10.

Mean least squared errors of Gappy-POD results versus number of sensors.

Table 2에는 본 연구에서 진행된 Gappy POD의 계산 시간이 정리되어 있다. POD-Kriging과의 비교를 위하여 Gappy POD를 위한 연산은 POD-Kriging과 동일한 장치를 활용하였다. 반응 표면을 미리 구성해야 하는 POD- Kriging과 다르게, Gappy POD는 센서 측정값을 기반으로 하여 전체 필드를 예측하기 때문에 반응 표면 구성을 위한 사전 연산이 필요하지 않다. 이번 연구에서는 Gappy POD를 활용하여 하나의 Favre 평균 온도장을 예측하기 위해 약 440초의 시간이 소요되었다. 이번 연구에서 활용한 센서 개수 범위 내에서는 센서 개수와 Gappy POD의 계산 시간 사이의 분명한 경향이 드러나지 않았다.

Table 2.

Computational times of the predictions of the data sets of Favre mean temperature fields by Gappy-POD with sensors placed in the domain

Number of Sensors	Computational time (s)
	Total	Per case
	Total	Mean	Standard deviation
32	13,248	441.6	64.9
128	13,139	438.0	74.9
512	13,113	437.1	81.3

4.4 예측 결과 분석

Fig. 11은 $8^{2}$ 개의 그리드 개수를 적용한 POD-Kriging 및 32개의 센서를 적용한 Gappy POD로 예측한 검증케이스의 Favre 평균 온도장을 보여준다. 해당 검증 케이스는 16.82%의 과잉 공기율과 52.25°의 swirl 각도가 운전조건으로 적용되었다. 해당 검증 케이스에 대하여 POD-Kriging은 CFD 결과 대비 4.5%의 최소 제곱 오차율을 보였으며, Gappy POD는 벽면 센서 활용 시 7.5%, 내부 배치 센서 활용 시 6.7%의 오차율을 보였다. 상대적으로 낮은 오차율을 보이는 POD-Kriging이 CFD 결과 나타난 온도 분포를 가장 유사하게 예측하는 것을 Fig. 11(b)를 통해 확인할 수 있다. 벽면 센서를 활용한 Gappy POD 예측 결과를 나타내는 Fig. 11(c)는 CFD 결과 대비 가장 상이한 분포를 보였다.

https://static.apub.kr/journalsite/sites/kosco/2021-026-02/N0590260201/images/ksssf_26_02_01_F11.jpg

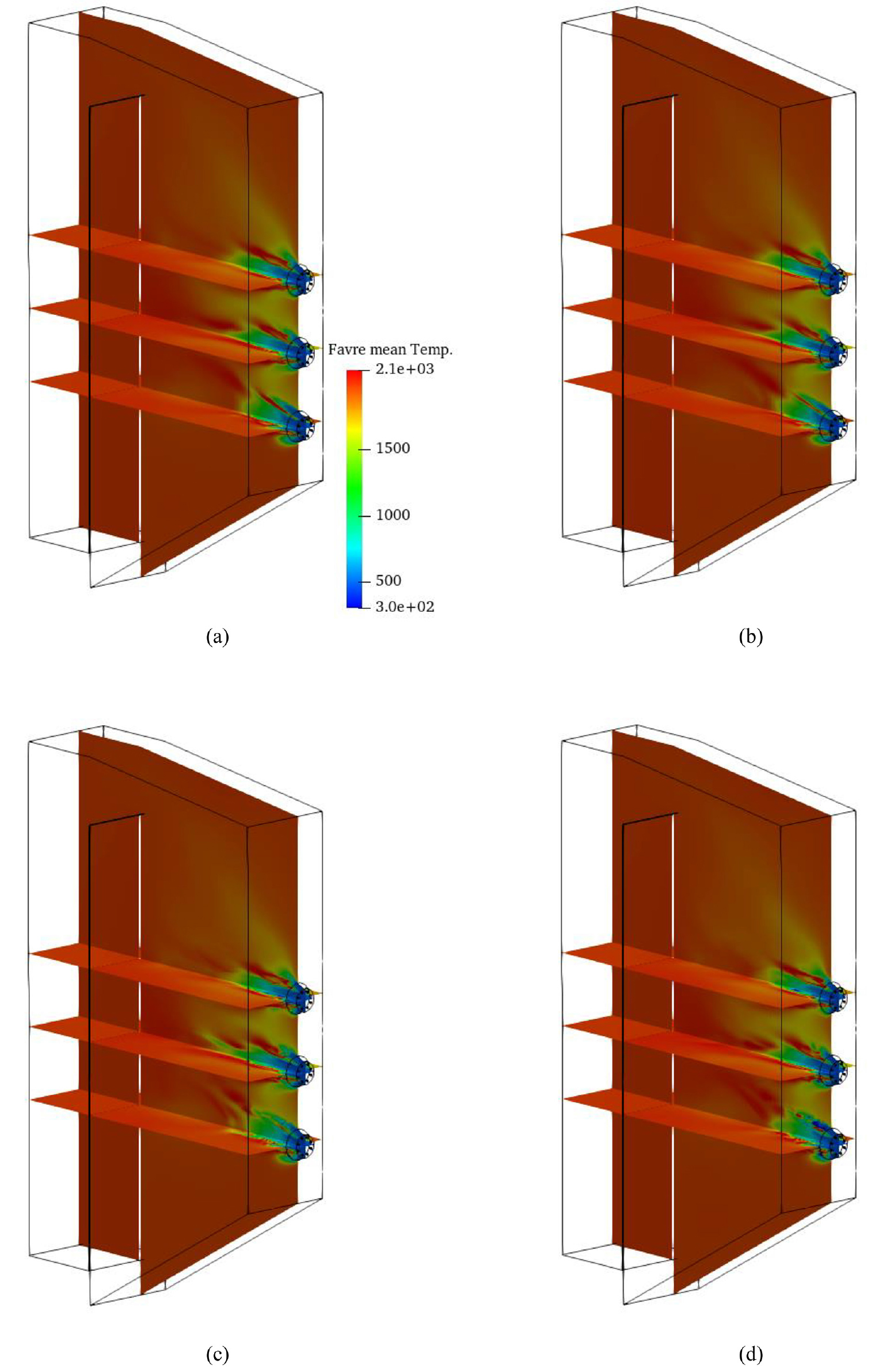
Fig. 11.

Favre mean temperature fields of a validation case, in which 16.82% of excess air and 52.25° of swirl vane angle are applied as operating conditions, obtained by (a) CFD, (b) POD-Kriging with 8² grids, (c) Gappy POD with 32 sensors on the wall and (d) Gappy POD with 32 sensors in the domain. The unit is K.

5. 결 론

본 연구는 POD-Kriging 및 Gappy POD로 구축된 ROM의 발전용 천연가스 보일러의 정상상태 운전조건 분석으로의 실용성을 검토하였다. 2차원 파라미터 공간 내에서 LHS와 adaptive sampling을 적용하여 결정된 20개의 운전조건에 대응하는 수치해석 결과를 학습하여 ROM이 구축되었다. ROM의 예측 정확도 검증을 위해 10개의 추가 운전조건 및 이들에 대응하는 수치해석 결과들을 확보하였으며, 이들을 검증용 데이터로 활용하였다. 20개의 학습용 데이터 행렬의 특이값 분해로 POD mode를 확보하였으며, 특이값 누적 상위 99% 이상을 만족하는 19개의 POD mode만을 스칼라 유동장 예측에 활용하였다.

POD-Kriging에서 그리드 개수가 많을수록 훈련오차는 줄어들지만, 예측오차는 특정 수준 이하의 오차율을 보이지 않았다. 새로운 운전조건의 예측 정확도를 측정하는 지표인 예측오차의 하한선이 분명한 점은 POD-Kriging의 최대 성능 수준이 정해져 있음을 의미한다. 그리드 개수가 많으면 반응 표면 생성을 위한 계산 시간을 비약적으로 상승시키는 사실 또한 확인하였다. 종합적으로, POD-Kriging의 적용을 위해서 최저수준의 예측오차와 계산 시간 사이에서 절충되는 그리드 개수를 설정할 필요가 있음을 확인하였다.

Gappy POD의 실제 적용성 평가를 위해서 센서 부착 가능한 위치를 보일러 벽면으로 가정한 후, 벽면 배치된 센서들만으로 얻은 Gappy POD 결과의 예측오차와 훈련오차를 검토하였다. 보일러 벽면 배치 센서들을 활용한 결과들은 보일러 내부 배치 센서들을 활용한 결과들에 비해 대체적으로 높은 오차를 보였고, 모두 10% 이내의 오차율을 보였다. 이는 벽에 센서를 배치하였어도 Gappy POD를 이용한 ROM을 실용적으로 활용할 수 있음을 보여준다. 또한, 센서의 개수는 일정 개수 이상의 센서를 활용하면 예측오차 및 훈련오차의 변동이 크지 않았다.

References

Monthly OECD electricity statistics, International Energy Agency, 2020.

X. Yuan, C. Ou, Y. Wang, C. Yang, W. Gui, A Layer-Wise Data Augmentation Strategy for Deep Learning Networks and Its Soft Sensor Application in an Industrial Hydrocracking Process, IEEE T. Neur. Net. Lear., (2019) 10.1109/TNNLS.2019.295170831841424

G. Aversano, A. Bellemans, Z. Li, A. Coussement, O. Gicquel, A. Parente, Application of reduced-order models based on PCA &Kriging for the development of digital twins of reacting flow applications, Comput. Chem. Eng., 121 (2019) 422-441. 10.1016/j.compchemeng.2018.09.022

G. Aversano, M. Ferrarotti, A. Parente, Digital twin of a combustion furnace operating in flameless conditions: reduced-order model development from CFD simulations, P. Combust. Inst., (In Press) 2020. 10.1016/j.proci.2020.06.045

L. Sirovich, M. Kirby, Low-dimensional procedure for the characterization of human faces, J. Opt. Soc. Am., A 4(3) (1987) 519-524. 10.1364/JOSAA.4.0005193572578

K. Fukunaga, Introduction to statistical pattern recognition, Elsevier, 2013.

L. Sirovich, Turbulence and the dynamics of coherent sturctures. I. Coherent structures, Q. Appl. Math., 45(3) (1987) 561-571. 10.1090/qam/910462

P. Holmes, J.L. Lumley, G. Berkooz, C.W. Rowley, Turbulence, coherent structures, dynamical systems and symmetry, Cambridge University Press, 2012.

M. Romanowski, Reduced order unsteady aerodynamic and aeroelastic models using Karhunen-Loeve eigenmodes, 6^th Symposium on Multidisciplinary Analysis and Optimization, 1996, 3981. 10.2514/6.1996-3981

G. Berkooz, P. Holmes, J.L. Lumley, The proper orthogonal decomposition in the analysis of turbulent flows, Annu. Rev. Fluid Mech, 25(1) (1993) 539-575. 10.1146/annurev.fl.25.010193.002543

R. Everson, L. Sirovich, Karhunen-Loeve procedure for gappy data, J. Opt. Soc. Am. A, 12(8) (1995) 1657-1664. 10.1364/JOSAA.12.001657

K. Cohen, S. Siegel, T. McLaughlin, Sensor placement based on proper orthogonal decomposition modeling of a cylinder wake, 33^rd AIAA Fluid Dynamics Conference and Exhibit, 2003, 4259. 10.2514/6.2003-4259

K. Willcox, Unsteady flow sensing and estimation via the gappy proper orthogonal decomposition, Comput. Fluids, 35(2) (2006) 208-226. 10.1016/j.compfluid.2004.11.006

P. Kumar, Y.M. El Sayed, R. Semaan, Optimized sensor placement using stochastic estimation for a flow over a 2D airfoil with Coanda blowing, 7^th AIAA Flow Control Conference, 2014, 2101. 10.2514/6.2014-2101

P.G. Constantine, E. Dow, Q. Wang, Active subspace methods in theory and practice: applications to kriging surfaces, SIAM J. Sci. Comput., 36(4) (2014) A1500- A1524. 10.1137/130916138

B. Yildirim, C. Chryssostomidis, G.E. Karniadakis, Efficient sensor placement for ocean measurements using low-dimensional concepts, Ocean Model., 27 (3-4) (2009) 160-173. 10.1016/j.ocemod.2009.01.001

T.H. Shih, W.W. Liou, A. Shabbir, Z. Yang, J. Zhu, A new k-ε eddy viscosity model for high reynolds number turbulent flows, Comput. Fluids, 24(3) (1995) 227-238. 10.1016/0045-7930(94)00032-T

R. Jin, W. Chen, T.W. Simpson, Comparative studies of metamodelling techniques under multiple modelling criteria, Struct. Multidiscip., O. 23(1) (2001) 1-13. 10.1007/s00158-001-0160-4

M. Guénot, I. Lepot, C. Sainvitu, J. Goblet, R.F. Coelho, Adaptive sampling strategies for non-intrusive POD- based surrogates, Eng. Computation., 30(4) (2013) 521-547. 10.1108/02644401311329352

Journal of The Korean Society Combustion ISSN:1226-0959(Print) 2466-2089(Online) 한국연소학회지

Preview

Digital Twin for Prediction of the Steady State Temperature Field of a Natural Gas Boiler

ABSTRACT

MAIN

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

(13)

Fig. 1.

(a) Computational mesh of the target gas boiler and (b) its burner section.

Table 1.

Burner operating conditions

Fig. 2.

Directions of swirl inlet flows corresponding to two swirl vane angles: 0.45 degree and 57.15 degree.

(14)

(15)

(16)

(17)

(18)

(19)

(20)

(21)

(22)

(23)

(24)

Fig. 3.

Map of 20 samples and 10 validation cases in 2D parametric space.

Fig. 4.

Schematic diagram of coefficients prediction by Kriging.

Fig. 5.

Locations of the 32 sensors placed (a) on the wall and (b) in the domain.

Fig. 6.

Singular values and cumulative energy captures for POD modes.

Fig. 7.

Visualization of (a) mode 1 and (b) mode 2.

Fig. 8.

Mean least squared errors of POD-Kriging results versus number of grids in the parametric space and corresponding standard deviations. The standard deviations are indica- ted as error bars.

(25)

Fig. 9.

Computational times of the predictions of the data sets of Favre mean temperature fields (comprised with 20 samples and 10 validation cases) by POD-Kriging.

Fig. 10.

Mean least squared errors of Gappy-POD results versus number of sensors.

Table 2.

Computational times of the predictions of the data sets of Favre mean temperature fields by Gappy-POD with sensors placed in the domain

Fig. 11.

References