Artificial Neural Network for the Representation of Chemical Kinetics in Reactive Flows

Jeongyong Lee; Bok Jik Lee

doi:10.15231/jksc.2022.27.1.017

Preview

Research Article

Journal of The Korean Society Combustion. 31 March 2022. 17-26
https://doi.org/10.15231/jksc.2022.27.1.017

Artificial Neural Network for the Representation of Chemical Kinetics in Reactive Flows

인공신경망을 이용한 반응유동 수치해석의 반응기구 대체 연구

Jeongyong Lee¹

Bok Jik Lee²^*

이 정용¹

이 복직²^*

¹Interdisciplinary Program in Space Systems, Seoul National University

²Institute of Advanced Aerospace Technology, Seoul National University

¹서울대학교 협동과정 우주시스템전공

²서울대학교 항공우주신기술연구소

^{*Corresponding Author}

ABSTRACT

Reducing the computational cost of chemical kinetics is essential to implement detailed reaction mechanisms into realistic numerical simulations. The present study introduces an artificial neural network (ANN) that can predict the chemical source terms of each species for the given species mass fractions and temperature, replacing the conventional chemical terms based on Arrhenius rate equations. The ANN was trained using numerical solutions of opposed-flow flames that can cover a wide range of combustion problems. The OPPDIF code and a detailed reaction mechanism for hydrogen and air with 9 species and 19 reactions were used to generate a training dataset comprised of species mass fractions, temperature, chemical source terms. A physics-guided loss function that considers mass conservation of elemental species was employed. Using the trained ANN, a modified OPPDIF, named OPPDIF-ANN, was prepared by replacing the CKWYP with CKWYP-ANN evaluating the chemical sources via the trained ANN. For multiple global strain rate conditions, the solutions using ANN-based source terms were proven to be identical to those using Arrhenius source terms.

Keywords

Machine learning

Artificial neural network

Chemical kinetics

Opposed-flow diffusion flames

MAIN

1. 서 론
2. 수치해석 기법
3. 기계학습 기법
3.1 인공신경망
3.2 변수 선정 및 데이터 세트 구축
3.3 데이터 전처리 과정
3.4 신경망 모델링
4. 결 과
4.1 신경망 학습 정도 평가
4.2 신경망 예측 성능 평가
4.3 신경망 계산 효율성 평가
4.4 신경망 응용성 확인
5. 결 론

1. 서 론

연소 화학반응의 상세반응기구에 대한 정보는 발전을 거듭하여 수천 개에 이르는 화학종과 수만 개의 화학반응으로 구성된 모델링이 등장하고 있다. 그러나 이러한 모델링을 직접 수치해석에 활용할 때에는 막대한 계산비용이 발생하게 된다[1]. 최근에 반응유동 수치해석의 막대한 계산비용을 줄이기 위해 intrinsic low-dimensional manifolds(ILDM)[2], look-up table(LUT)[3], in situ adaptive tabulation(ISAT)[4] 등의 테이블 내삽 기법들이 연구되고 있다. 그러나 ILDM, LUT, ISAT 기법은 대용량의 메모리를 사용하며[5], 이를 고차원 테이블(multi-dimension table)로 사용했을 때에는 계산 속도가 느려지고 내삽 오류도 발생한다는 단점이 있다[6].

인공신경망(Artificial Neural Network, ANN)은 복잡한 비선형 함수들을 쉽게 모델링할 수 있어[7], 최근 이를 활용하여 반응유동 수치해석의 계산비용을 줄이는 연구가 다수 진행되고 있다[8,9,10,11,12].

Christo 등[8]은 인공신경망을 활용하여 난류 화염에서 화학반응에 의한 화학종 조성(Species composition) 변화를 예측하였다. 난류 제트 확산 화염의 PDF/Monte Carlo 해석에서 인공신경망은 direct integration(DI) 기법과 LUT 기법보다 빠른 계산 속도를 보였다.

Blasco 등[9]은 4개의 화학반응과 7개의 화학종으로 구성된 메탄 축소반응기구를 대체하여 시간에 따라 변화되는 화학종의 조성과 온도 및 밀도를 예측할 수 있는 인공신경망을 구축하였다. 인공신경망은 DI 기법보다 빠른 계산 속도를 보였으며, 테이블 내삽 기법보다 RAM 메모리를 덜 사용하였다.

Sen 등[10,11]은 인공신경망을 반응유동의 LES 해석에 접목하였다. Sen 등[10]의 연구에서 인공신경망은 DI 기법보다 약 5.5배 빠르게 반응속도를 산출하였을 뿐만 아니라 인공신경망이 탑재된 유동 해석자는 DNS와 유사하게 소염 및 재점화 현상을 포착하였다. 또한, Sen 등[11]은 인공신경망이 탑재된 유동 해석자를 통해 난류 예혼합 화염에서 발생하는 화염-난류 상호작용을 해석하였고 이는 DVODE(Double-precision Variable-coefficient Ordinary Differential Equation solver)를 사용했을 때보다 약 3.5배 빠른 계산 속도를 보였다.

최근 Wan 등[12]은 인공신경망을 반응유동의 DNS 해석에 접목하였다. 인공신경망은 CVODE(C-language Variable- coefficient Ordinary Differential Equation Solver)를 대체하였으며 2차원 DNS 해석에서 GRI 3.0 상세반응기구[13]보다 25배 빠른 계산 속도를 보였다.

앞서 제시된 선행 연구 사례들은 신경망에 학습시킨 시간 간격(Time step)에 대해서만 적용이 가능하다는 한계점이 존재한다. 이에 본 연구에서는 범용성을 위해 기존 아레니우스 기반의 생성률 산출 기법을 대체하여 화학종의 생성률을 예측할 수 있는 인공신경망을 제시한다. 제시된 인공신경망의 예측 정확도와 계산 효율성을 평가하기 위해 기존 아레니우스 기반의 생성률 산출 기법과 비교하였다. 또한 인공신경망의 응용성을 확인하기 위해 본 연구에서 제시된 인공신경망을 CHEMKIN OPPDIF code[14]에 탑재한 후 수치해석을 수행하였다.

2. 수치해석 기법

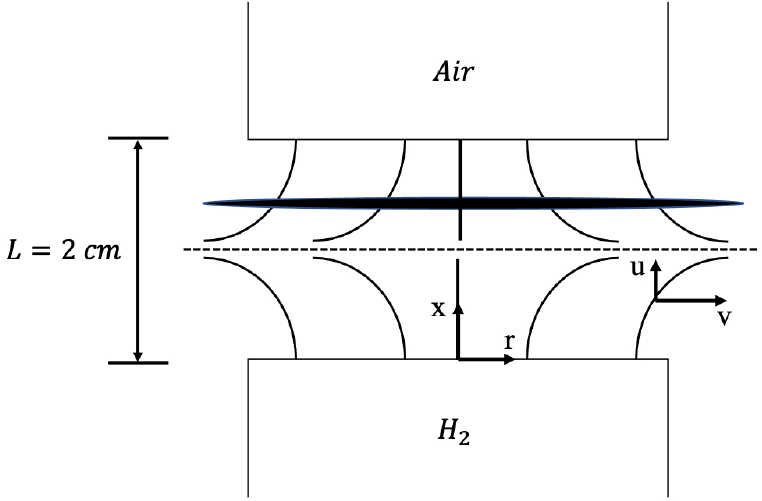
본 연구에서는 대향류 확산 화염해를 학습시킨 인공신경망을 제시하였다. 대향류 확산 화염은 상사를 통해 1차원 화염으로 모델링할 수 있어 쉽게 수치해석을 진행할 수 있다. 또한 대향류 확산 화염은 canonical flame의 일종으로 이를 학습시킨 인공신경망은 다양한 연소해석 문제에 적용될 수 있을 것으로 예상된다. Fig. 1은 대향류 확산 화염의 구조를 나타낸다. 연료와 산화제 사이 간격은 2 cm로 설정하였다. 상부 노즐에서는 산화제인 공기가 공급되었으며 하부 노즐에서는 연료인 수소가 공급되었다. 수치해석에는 대향류 확산 화염 해석에 적합한 CHEMKIN OPPDIF code를 사용하였고, 화학반응기구로는 9개의 화학종과 19개의 화학반응으로 구성된 수소/공기 상세반응기구[15]를 사용하였다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F1.jpg

Fig. 1.

Schematic diagram of opposed-flow diffusion flame.

3. 기계학습 기법

3.1 인공신경망

인공신경망은 기계학습 방법론의 일종으로 뇌와 같은 생물학적 신경 시스템이 정보를 처리하는 방식에서 영감을 받은 연산모델이며 예측, 이미지 또는 패턴 인식, 분류 등의 분야에서 널리 사용되고 있다[16].

인공신경망은 입력층(Input layer), 은닉층(Hidden layer), 출력층(Output layer)으로 구성 되어 있으며, 각 층은 뉴런으로 이루어져 있다. 인공신경망은 순전파(Forward propagation)와 역전파(Back propagation) 과정을 통해 학습된다. 순전파 과정은 인공신경망에 입력된 값이 입력층, 은닉층, 출력층으로 전파되는 과정으로 식 (1)과 같이 나타낼 수 있다.

(1)

Y = h (W X + b)

식 (1)에서 X와 Y는 입력값과 예측값을 나타내며 h, W, b는 각각 활성화 함수, 가중치, 바이어스를 나타낸다. 순전파 과정은 각 뉴런의 입력값에 가중치를 곱하고 바이어스를 더한 다음, 활성화 함수를 적용하여 출력값을 계산한다. 오차 역전파는 출력값과 목표값 사이의 오차를 계산한 후 오차를 역방향으로 전파하여 뉴런을 잇는 연결선의 가중치 값을 조정하는 과정이다. 신경망 학습은 이 과정을 통해 출력값과 목표값 사이의 오차를 최소화하는 방향으로 진행된다. Fig. 2는 인공신경망의 구축 과정을 설명하는 도식이다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F2.jpg

Fig. 2.

Overview of the artificial neural network approach.

3.2 변수 선정 및 데이터 세트 구축

화학반응속도론(Chemical kinetics)에 의하면 화학종의 생성률은 식 (2)와 같이 온도, 압력, 질량분율에 대한 함수로 나타낼 수 있다. 본 연구에서는 압력이 1기압인 등압조건을 사용하였기 때문에 압력은 입력 변수에서 제외되었다.

(2)

{\dot{ω}}_{i} = \frac{\partial Y_{i}}{\partial t} = f (T, P, Y_{H_{2}}, Y_{H}, \dots, Y_{H_{2} O})

이에 신경망의 입력 변수는 질소를 제외한 8개의 화학종에 대한 질량분율(Y_H2, Y_H, Y_O2, Y_O, Y_OH, Y_HO2, Y_H2O2, Y_H2O)과 온도로 설정하였다. 출력 변수는 입력 변수에 해당되는 화학종에 대한 생성률로 설정하였고 생성률의 단위는 mole/cm³-s이다.

본 연구에서는 CHEMKIN OPPDIF code를 활용하여 데이터 세트를 구축하였다. 화염 신장률에 따라 화염 구조가 변하기 때문에 연료 입구 속도와 산화제 입구 속도를 변경시킴으로써 다양한 화염구조 데이터를 수집하였다. 전체 화염 신장률을 0 s^-1에서 소염 현상이 발생되는 12,000 s^-1 전까지 100 s^-1씩 증가시키면서 계산을 진행하였고 각 계산에서는 적응격자(Adaptive grid)를 통해 300개와 400개 사이의 격자수가 사용되었다. 이를 통해 총 44,072개의 케이스로 구성된 학습 데이터 세트를 구축하였다.

3.3 데이터 전처리 과정

데이터 전처리 과정으로 중복 케이스 제거, 데이터 정규화(Data normalization), 데이터 세트 분리(Data splitting) 과정을 진행하였다. 본 연구에서는 신경망의 학습 시간을 단축시키기 위해 중복 케이스를 제거하였다.

데이터 정규화 과정은 모든 데이터를 동일한 스케일로 변환시키는 과정으로 학습 전 이를 활용하여 신경망의 예측 성능을 개선시킬 수 있다[17]. 본 연구에서는 최소 최대 정규화 기법(Min-Max Normalization)을 활용하여 모든 데이터를 -1과 1 사이의 값으로 변환시켰다. 식 (3)은 본 연구에서 사용된 정규화 기법의 식을 보여주며, x_norm는 정규화 기법을 통해 변환된 데이터를 나타낸다.

(3)

x_{n o r m} = \frac{x - x_{\min}}{x_{\max} - x_{\min}} \times 2 - 1

본 연구에서는 데이터 세트를 학습 데이터 세트(Training dataset), 검증 데이터 세트(Validation dataset), 시험 데이터 세트(Test dataset)로 분리하였다. 학습 데이터 세트, 검증 데이터 세트, 시험 데이터 세트는 각각 전체 데이터 세트의 81%, 9%, 10%를 차지하였다. 학습 데이터 세트는 신경망 학습에 사용되었으며, 검증 데이터 세트는 학습 중 신경망 하이퍼파라미터의 성능을 평가하는데 사용되었다. 시험 데이터 세트는 신경망 학습 후 신경망의 예측 성능을 평가하는데 사용되었다.

3.4 신경망 모델링

신경망 하이퍼파라미터를 선정하는 방법에는 설계자의 직관과 경험에 의존하는 시행착오법 또는 베이지안 최적화(Bayesian optimization), 랜덤 탐색(Random search), 그리드 탐색(Grid search) 등의 최적화 기법이 있다. 본 연구에서는 베이지안 최적화를 사용하여 신경망 하이퍼파라미터를 최적화하였다. 베이지안 최적화는 그리드 탐색 또는 랜덤 탐색과는 다르게 관측된 정보를 반복 탐색 과정에 반영하여 주어진 모델의 최적 파라미터 조합을 탐색한다[18]. 본 연구에서는 100번의 반복 탐색 과정이 진행되었다. 탐색 과정에서는 학습률, 활성화 함수, 은닉층의 뉴런 수가 조정되었으며 본 연구에서는 가장 낮은 손실 함수(Loss function)를 생성하는 신경망 하이퍼파라미터 조합을 탐색하였다.

인공신경망은 파이썬 언어로 작성된 신경망 라이브러리인 Keras[19]를 활용하여 구축되었고 신경망 하이퍼파라미터는 Keras-Tuner[20]를 활용하여 최적화하였다. Keras-Tuner는 신경망 하이퍼파라미터를 조정하기 위해 개발된 파이썬 언어 기반의 오픈소스 라이브러리이다.

본 연구에서는 은닉층의 수는 3개로 설정하였으며 은닉층의 뉴런 수는 베이지안 최적화를 통해 결정되었다. Uzair 등[21]은 은닉층의 수가 3개일 때 신경망이 시간 복잡도와 정확도 측면에서 최적의 성능을 낼 수 있다고 밝혔다. 또한 본 연구에서는 여섯 종류의 학습률(1 × 10^-3, 5 × 10^-4, 3 × 10^-4, 1 × 10^-4, 5 × 10^-5, 3 × 10^-5, 1 × 10^-5)과 네 종류의 활성화 함수(Sigmoid, Hyperbolic tangent, Rectified Linear Unit, Exponential Linear Unit[22])가 고려되었다. 각 활성화 함수 적용시 epoch 당 학습에 약 0.9 s, 1 s, 0.6 s, 1 s가 소요된다. 본 연구의 활성화 함수 선정 기준은 손실 함수 최소화이며, 이에 가장 낮은 손실 함수를 보이는 Sigmoid 함수를 선정하였다. Table 1은 베이지안 최적화를 통해 탐색된 신경망 하이퍼파라미터 조합으로 탐색 과정에서 가장 낮은 손실 함수를 생성하였다.

Table 1.

ANN hyperparameter obtained by Bayesian optimization

The number of neurons	36, 28, 16
Activation function	Sigmoid
Learning rate	0.001

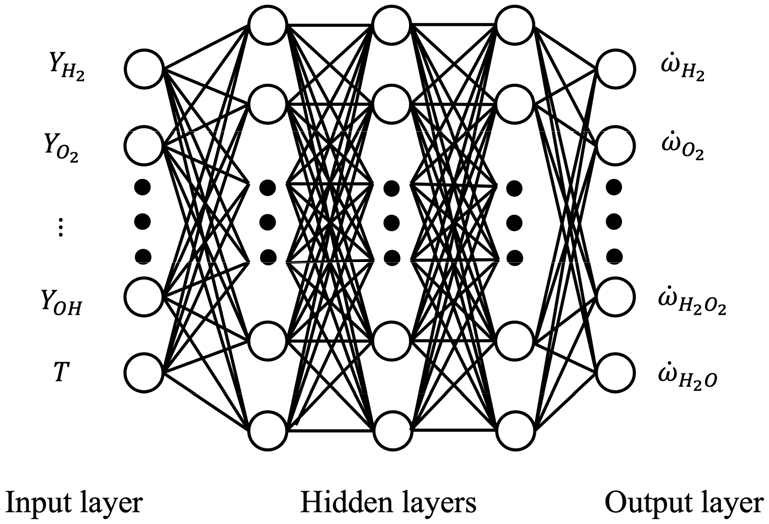
Fig. 3은 본 연구에서 사용된 인공신경망의 구조를 나타낸다. 신경망은 Fig. 3과 같이 한 개의 입력층, 세 개의 은닉층, 한 개의 출력층으로 구성되었다. 입력층을 구성하는 뉴런 수는 9개이며 화학종의 질량분율과 온도로 구성되었다. 출력층을 구성하는 뉴런 수는 8개이며 화학종의 생성률로 구성되었다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F3.jpg

Fig. 3.

Architecture of artificial neural network.

반복 횟수(Epochs)는 5000으로 설정하였지만 과대적합(Overfitting)을 방지하기 위해 사용된 early stopping 기능을 통해 반복 횟수가 641일 때 학습이 완료되었다. 과대적합은 신경망이 학습 데이터에 대해서는 좋은 성능을 보이지만 이외의 데이터에 대해서는 예측 성능이 떨어지는 현상이다[23]. Early stopping 기능은 검증 손실(Validation loss)을 모니터링하면서 학습 성능이 더 이상 개선되지 않는다고 판단될 때 자동적으로 학습을 멈추는 기능이다[24]. 또한 학습 알고리즘으로는 계산 효율이 높고 계산 요구량이 작은 Adam 알고리즘[25]을 사용하였다.

손실 함수는 출력값과 목표값의 오차를 계산하는 함수이며 신경망 학습은 손실 함수를 최소화하는 방향으로 진행된다. 그러나 신경망 학습에 사용되는 손실 함수들은 화학반응에서의 원소질량보존을 고려하지 않는다. 이에 본 연구에서는 이를 고려하기 위해 식 (6)과 같이 주로 사용되는 손실 함수인 평균 제곱 오차(Mean Squared Error, MSE)에 원소질량보존을 규제하는 항을 추가하였다. 식 (6)은 본 연구에서 사용된 손실 함수의 식을 나타내며 식 (7)은 평균 제곱 오차의 식을 나타낸다.

(6)

L = M S E + H_{t e r m} + O_{t e r m}

(7)

M S E = \frac{1}{n} \sum_{i = 1}^{n} ({\dot{ω}}_{i, p r e d} - t_{i})^{2}

(8)

H_{t e r m} = \sum_{H}^{} n_{m} | ({\dot{ω}}_{m, p r e d} + 1) ({\dot{ω}}_{m, \max} - {\dot{ω}}_{m, \min}) / 2 + {\dot{ω}}_{m, \min} |

(9)

O_{t e r m} = \sum_{O}^{} n_{k} | ({\dot{ω}}_{k, p r e d} + 1) ({\dot{ω}}_{k, \max} - {\dot{ω}}_{k, \min}) / 2 + {\dot{ω}}_{k, \min} |

식 (7)의 ${\dot{ω}}_{i, p r e d}$ 는 신경망의 출력값이며 t_i는 목표값이다. 본 연구의 입력 및 출력 변수에 해당되는 화학종은 수소 원자를 포함하고 있는 화학종과 산소 원자를 포함하고 있는 화학종으로 분류할 수 있다. 식 (6)의 H_term은 수소 원자와 관련된 항이고 O_term은 산소 원자와 관련된 항이다. 식 (8)의 $n_{m}, {\dot{ω}}_{m, pred}, {\dot{ω}}_{m, \max}, {\dot{ω}}_{m, \min}$ 은 각각 수소 원자를 포함하고 있는 화학종 m에 존재하는 수소 원자의 수, 화학종 m에 대한 신경망 출력값, 화학종 m에 대한 생성률 최댓값, 화학종 m에 대한 생성률 최솟값을 나타낸다. 식 (9)의 $n_{k}, {\dot{ω}}_{k, pred}, {\dot{ω}}_{k, \max}, {\dot{ω}}_{k, \min}$ 은 각각 산소 원자를 포함하고 있는 화학종 k에 존재하는 산소 원자의 수, 화학종 k에 대한 신경망 출력값, 화학종 k에 대한 생성률 최댓값, 화학종 k에 대한 생성률 최솟값을 나타낸다. 식 (8)과 식 (9)에서 신경망 출력값은 -1과 1 사이의 값으로 변환된 값이기 때문에 식 (3)을 활용하여 신경망 출력값을 원범위로 변환시켰다.

4. 결 과

4.1 신경망 학습 정도 평가

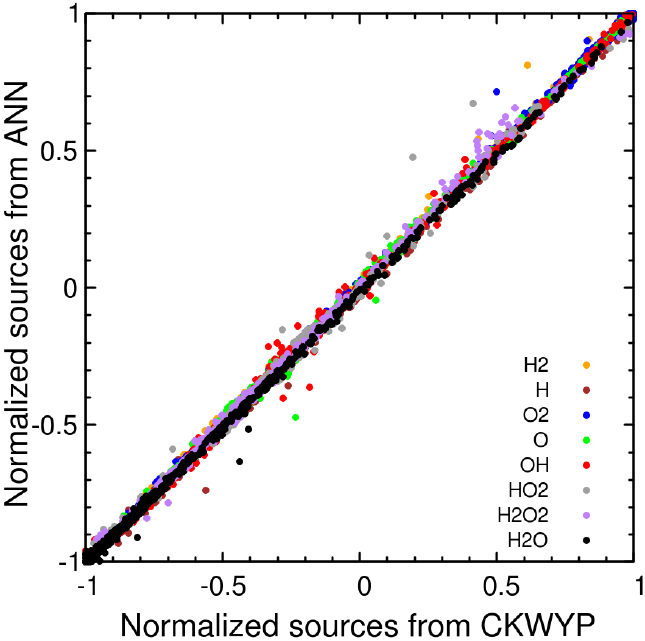
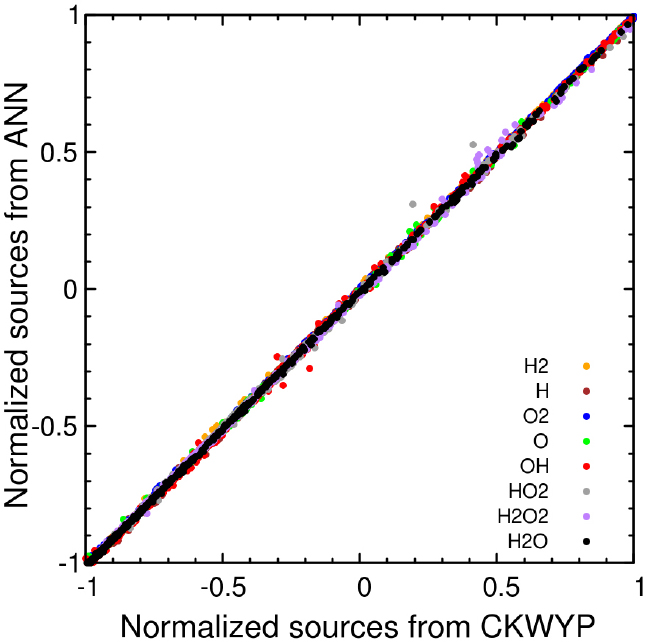
인공신경망의 학습 정도를 평가하기 위해 시험 데이터에 대한 신경망의 예측값과 목표값 사이의 결정계수(Coefficient of determination, R²)를 계산하였다. 결정계수는 모델의 정확도를 수치로 나타내는 척도로 사용되며 값이 1에 가까울수록 신경망 모델이 표본에 맞게 잘 학습되었다고 할 수 있다. Table 2와 Table 3은 각각 MSE와 MSE에 원소질량보존을 규제하는 항이 추가된 함수를 손실 함수로 사용했을 때 모든 화학종의 생성률에 대한 결정계수를 나타낸다. 이를 통해 원소질량보존을 규제하는 항이 추가된 함수를 손실 함수로 사용했을 때 결정계수가 1에 더 가까운 것을 확인할 수 있다. Fig. 4와 Fig. 5는 각각 MSE와 MSE에 원소질량보존을 규제하는 항이 추가된 함수를 손실 함수로 사용했을 때 시험데이터에 대한 예측값과 목표값 사이의 상관관계를 나타낸다. 이를 통해 원소질량보존을 규제하는 항이 추가된 함수를 손실 함수를 사용했을 때 시험데이터에 대한 예측값과 목표값 사이의 상관관계가 Y=X 선형모델에 더 근접한 것을 확인할 수 있다.

Table 2.

Coefficient of determination for each normalized chemical source terms with MSE

H₂	0.9992
H	0.9984
O₂	0.9990
O	0.9982
OH	0.9978
HO₂	0.9936
H₂O₂	0.9971
H₂O	0.9990

Table 3.

Coefficient of determination for each normalized chemical source terms with loss function considering the mass conservation of elemental species

H₂	0.9997
H	0.9987
O₂	0.9998
O	0.9987
OH	0.9982
HO₂	0.9975
H₂O₂	0.9979
H₂O	0.9992

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F4.jpg

Fig. 4.

Comparison of the ANN predictions on normalized chemical source terms of the 8 species against the normalized target values for the testing database unseen during training with MSE.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F5.jpg

Fig. 5.

Comparison of the ANN predictions on normalized chemical source terms of the 8 species against the normalized target values for the testing database unseen during training with loss function considering the mass conservation of elemental species.

4.2 신경망 예측 성능 평가

본 연구에서 구축된 인공신경망의 예측 성능을 평가하기 위해 기존 아레니우스 기반의 생성률 산출 기법과 비교하였다. CHEMKIN OPPDIF code에서 화학종의 생성률은 CKWYP 서브루틴을 통해 산출된다. 이에 본 연구에서는 CKWYP 서브 루틴을 대체하여 화학종의 생성률을 산출할 수 있는 CKWYP-ANN 서브루틴을 작성하였다.

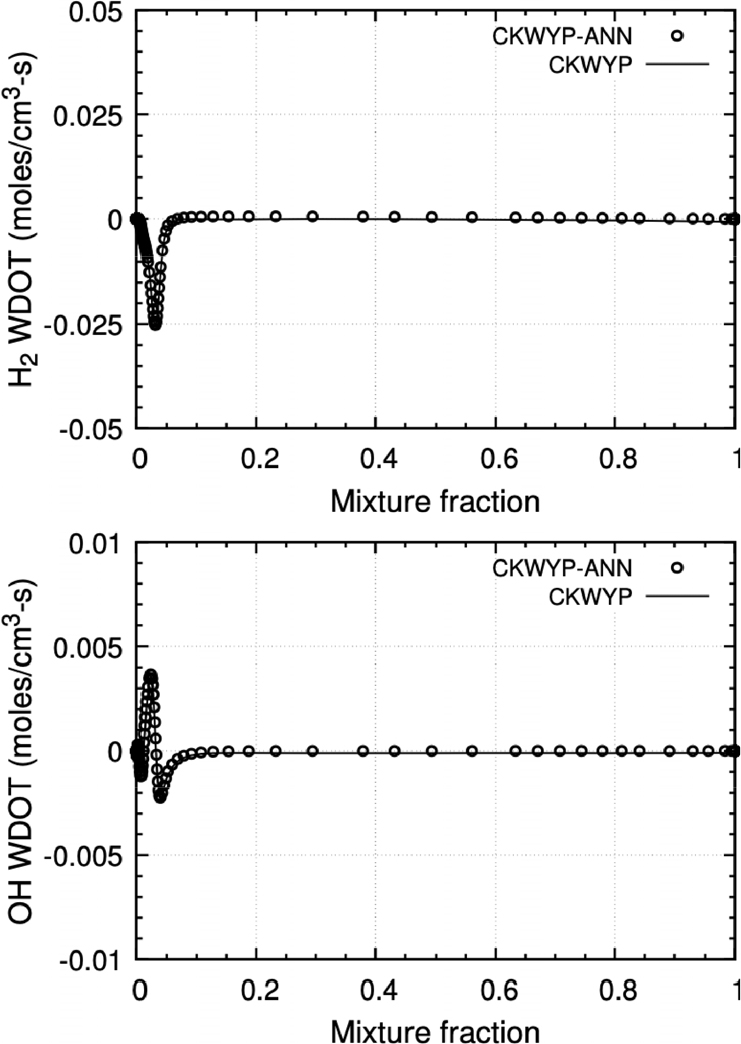
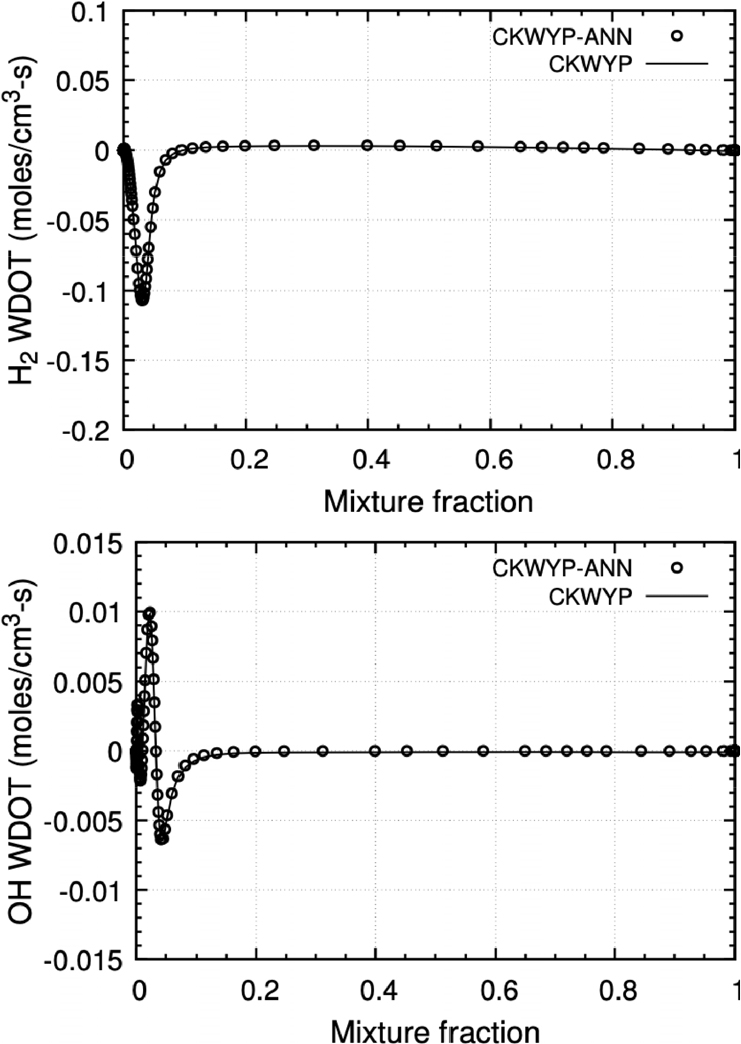
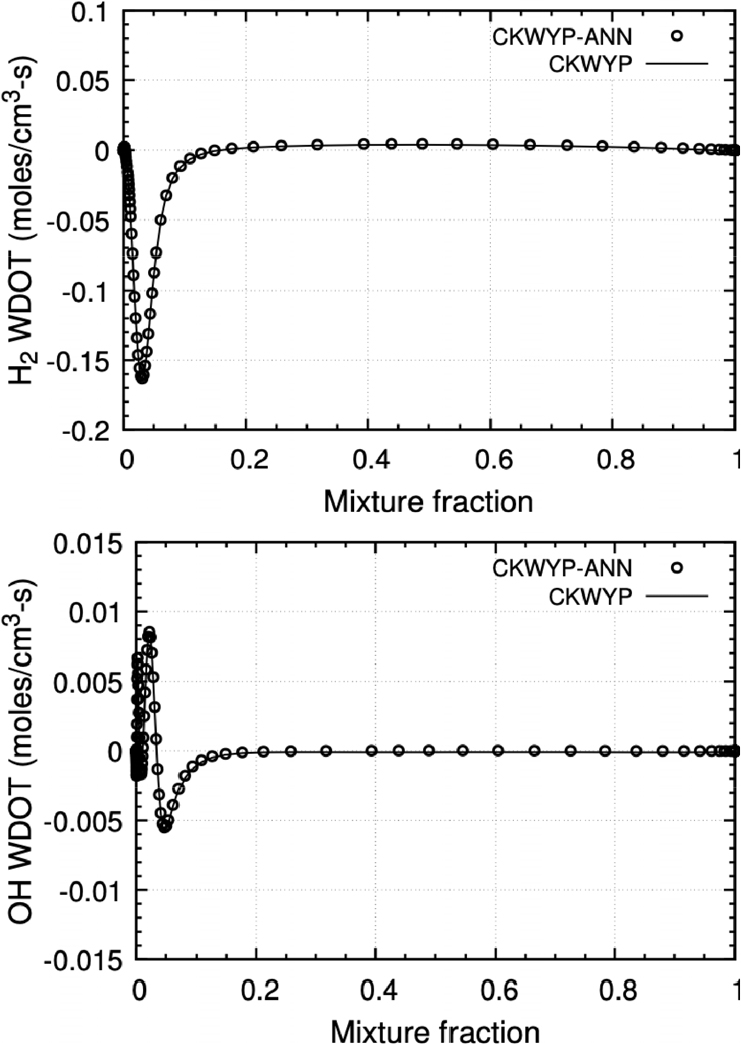
본 연구에서 구축된 신경망을 Fortran 언어에서 사용하기 위해 Fortran-Keras Bridge(FKB)[26] 라이브러리를 활용하였다. FKB 라이브러리는 Keras를 통해 구축한 신경망 모델을 Fortran 언어에서 사용할 수 있는 모델로 변환시켜준다. 본 연구에서는 주 화학종인 H₂의 생성률과 부 화학종인 OH의 생성률을 비교하였다. Fig. 6부터 Fig. 8은 각각 다른 전체 화염 신장률 조건에서 혼합분율에 따른 화학종의 생성률 분포를 나타내며 Table 4는 전체 화염 신장률 조건에 따른 CKWYP-ANN과 CKWYP 사이의 MSE를 나타낸다. 이를 통해 인공신경망이 화학종의 생성률을 정확하게 예측할 수 있다는 것을 확인하였다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F6.jpg

Fig. 6.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 1,055 s^-1.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F7.jpg

Fig. 7.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 5,550 s^-1.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F8.jpg

Fig. 8.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 10,955 s^-1.

Table 4.

MSE between chemical source terms obtained by CKWYP-ANN and CKWYP at the different global strain rates

Global strain rate	Species	MSE
1,055 s^-1	H₂	4.68 × 10^-7
1,055 s^-1	OH	9.35 × 10^-9
5,550 s^-1	H₂	4.52 × 10^-7
5,550 s^-1	OH	1.06 × 10^-8
10,955 s^-1	H₂	4.52 × 10^-7
10,955 s^-1	OH	9.49 × 10^-9

4.3 신경망 계산 효율성 평가

본 연구에서 구축된 신경망의 계산 효율성을 평가하기 위해 CKWYP와 CKWYP-ANN의 CPU time을 비교해보았다. 수소/공기 상세반응기구의 경우 CKWYP의 평균 소요 CPU time은 약 2.5 × 10^-5s이며 CKWYP-ANN의 평균 소요 CPU time은 약 1.5 × 10^-5 s로 CKWYP-ANN은 CKWYP보다 약 1.7배 빠르게 화학종의 생성률을 산출하였다.

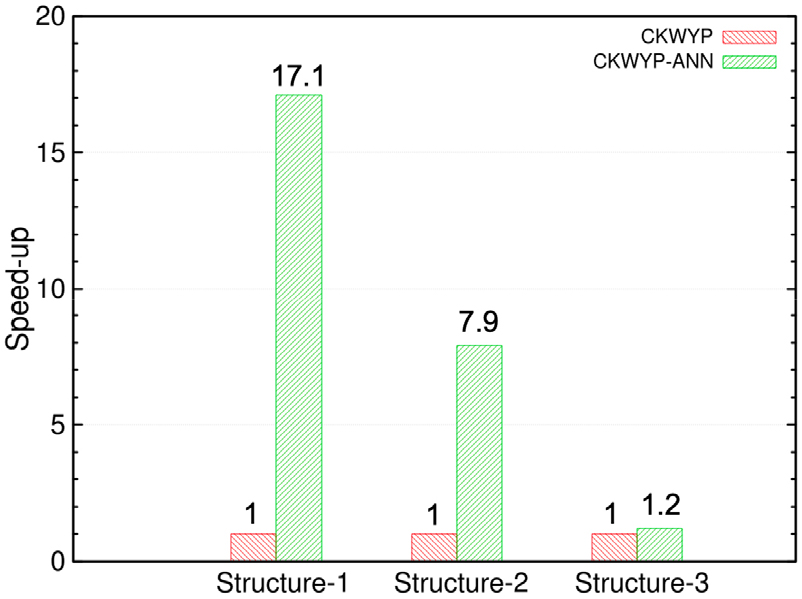
보다 큰 규모의 화학종 및 반응식을 포함하는 상세반응기구에 대해 신경망의 계산 효율성을 추가적으로 검증하고자 이를 GRI 3.0 상세반응기구에 적용해보았다. GRI 3.0 반응기구에 포함된 화학종 및 반응식의 수는 본 연구에서 사용된 수소/공기 상세반응기구에 포함된 화학종 및 반응식의 수보다 훨씬 많다. 은닉층의 수와 은닉층의 뉴런 수가 많을수록 신경망은 복잡한 문제를 해결할 수 있다[21]. 이에 인공신경망을 GRI 3.0 반응기구에 적용하기 위해 은닉층의 수를 증가시켰다. 또한 메모리를 더욱 효율적으로 사용하기 위해 은닉층의 뉴런 수는 2의 거듭제곱인 수들로 설정하였다[27]. Fig. 9는 인공신경망을 GRI 3.0 반응기구에 적용했을 때 신경망 구조에 따른 CKWYP-ANN의 speed -up을 나타낸다. Fig. 9에서 첫 번째 구조는 4개의 은닉층으로 구성되었으며 각 층을 구성하는 뉴런 수는 128, 64, 32, 16개이다. 두 번째 구조는 5개의 은닉층으로 구성되었으며 각 층을 구성하는 뉴런 수는 256, 128, 64, 32, 16개이다. 세 번째 구조는 6개의 은닉층으로 구성되었으며 각 층을 구성하는 뉴런 수는 512, 256, 128, 64, 32, 16개이다. Fig. 9를 통해 GRI 3.0 반응기구의 경우 세 번째 구조보다 복잡하지 않은 구조를 사용한다면 CKWYP-ANN이 CKWYP보다 빠르게 생성률을 산출할 수 있다는 것을 확인하였다. 추후 이를 바탕으로 GRI 3.0 반응기구에 적용할 수 있는 인공신경망을 구축할 예정이다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F9.jpg

Fig. 9.

Speed-up between CKWYP and CKWYP- ANN for GRI-Mech 3.0.

4.4 신경망 응용성 확인

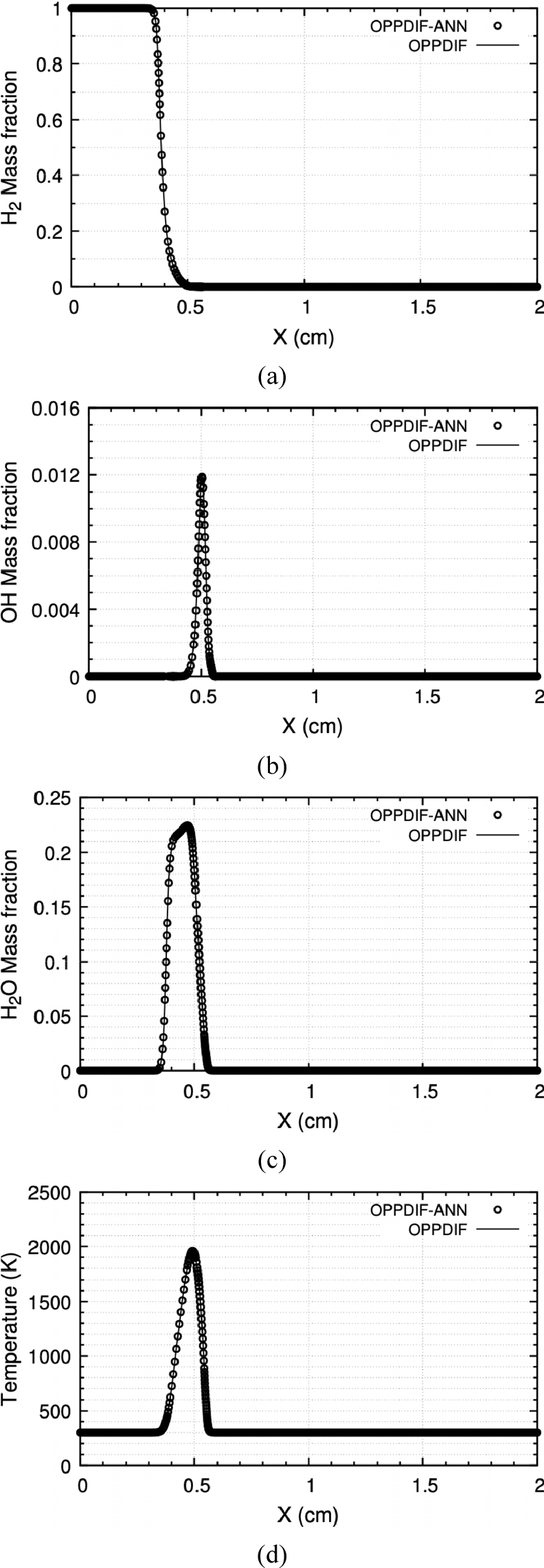
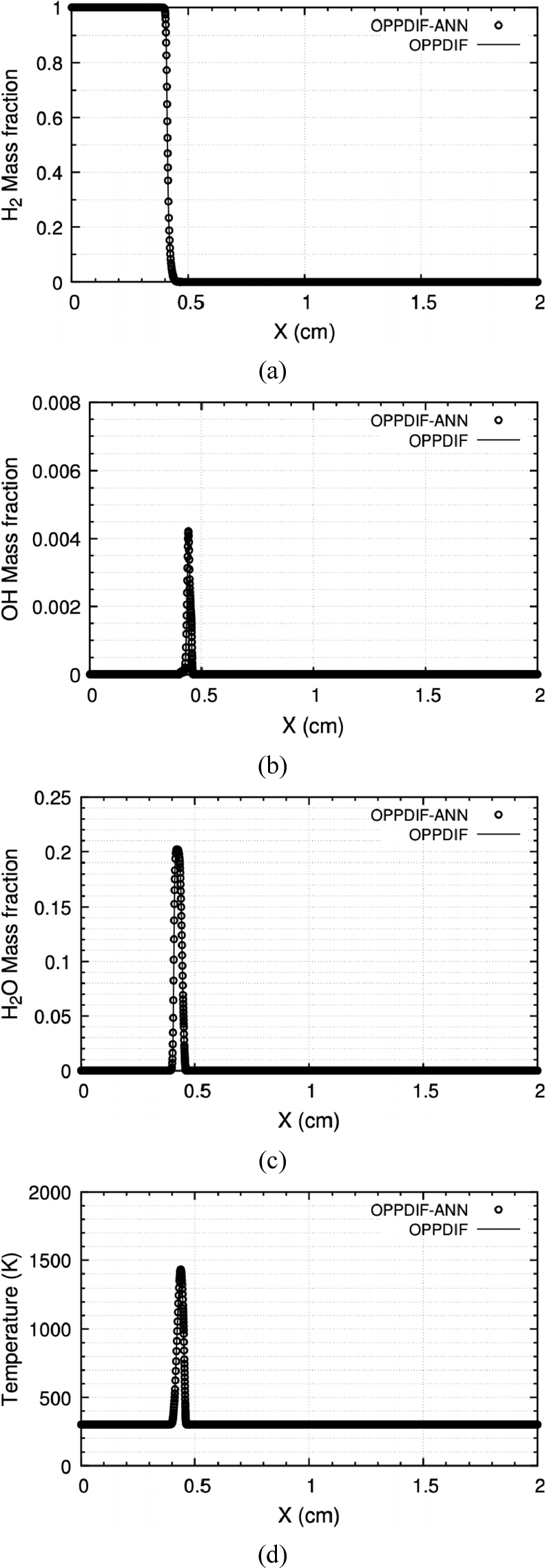
본 연구에서 구축된 신경망의 응용성을 평가하기 위해 인공신경망을 CHEMKIN OPPDIF code에 탑재한 후(OPPDIF-ANN) 수치해석을 수행하였다. OPPDIF-ANN은 CKWYP 서브루틴 대신 CKWYP -ANN 서브루틴을 통해 산출된 화학종의 생성률을 사용해 화염해를 구했다. Fig. 10부터 Fig. 12는 각각 다른 전체 화염 신장률 조건에서 위치에 따른 화학종의 질량분율과 온도 분포를 나타내며 Table 5는 전체 화염 신장률 조건에 따른 OPPDIF-ANN과 OPPDIF 사이의 MSE를 나타낸다. 이를 통해 OPPDIF-ANN은 화염 구조를 정확하게 재현할 수 있다는 것을 확인하였다.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F10.jpg

Fig. 10.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 1,055 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F11.jpg

Fig. 11.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 5,550 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.

https://static.apub.kr/journalsite/sites/kosco/2022-027-01/N0590270103/images/ksssf_27_01_03_F12.jpg

Fig. 12.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 10,955 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Table 5.

MSE between target values obtained by OPPDIF-ANN and OPPDIF at the different global strain rates

Global strain rate	Target	MSE
1,055 s^-1	Y_H2	5.20 × 10^-15
	Y_OH	5.69 × 10^-19
	Y_H2O	3.41 × 10^-15
	T	4.96 × 10^-14
5,550 s^-1	Y_H2	1.65 × 10^-12
	Y_OH	5.04 × 10^-16
	Y_H2O	5.44 × 10^-13
	T	5.46 × 10^-13
10,955 s^-1	Y_H2	6.83 × 10^-12
	Y_OH	1.24 × 10^-15
	Y_H2O	1.02 × 10^-11
	T	1.37 × 10^-10

한편, 1차원 정상화염 해석자를 이용하여 화염해를 얻기 위해서는 다변수 비선형 방정식의 해를 구하는 Newton- Rhapson 과정이 필요하다. 이에 따라 최종 수렴해를 얻기까지는 OPPDIF-ANN이 OPPDIF보다 약 2.9배의 시간을 소요하며, 인공신경망을 이용한 생성률 산출에 의한 오차가 해의 최종 수렴에는 결과적으로 불리하게 작용함을 확인하였다. 그러나, 일반적인 전산유체역학 해석자에서 비정상해의 산출을 위해 시간전진을 하는 경우에는 인공신경망을 이용한 생성률 산출비용감소가 여전히 유효할 것으로 판단된다.

본 연구에서는 평형한계와 소염한계 strain rate 범위를 학습하여 학습범위를 벗어나는 조건의 화염을 원천적으로 배제하였으며, 화학반응의 높은 비선형성으로 인해 인공신경망에 의한 생성률 산출 기법이 학습범위 바깥의 외삽에 적용될 경우 그 예측성능을 보장할 수 없다는 한계가 존재한다.

5. 결 론

본 연구에서는 기존 아레니우스 기반의 생성률 산출 기법을 대체할 수 있는 인공신경망을 제시하였다. CHEMKIN OPPDIF code를 활용하여 학습 데이터 세트를 구축하였고 데이터 전처리 과정으로는 중복 케이스 제거, 데이터 정규화, 데이터 세트 분리를 진행하였다. 신경망 학습 과정에서 화학반응에서의 원소질량보존을 고려하기 위해 기존 손실 함수에 원소질량보존을 규제하는 항을 추가하였다.

본 연구에서 제시된 인공신경망의 예측 성능과 계산 효율성을 확인하기 위해 기존 아레니우스 기반의 생성률 산출 기법과 비교하였다. 인공신경망은 기존 기법보다 빠른 계산 속도를 보이면서 화학종의 생성률을 정확하게 예측할 수 있었다. 또한 인공신경망은 확산화염의 1차원 정상해 해석자에 탑재되었을 때 화염 구조를 정확하게 재현할 수 있었다.

추후에는 본 연구에서 구축된 신경망을 전산유체역학 해석 코드에 탑재하여 다양한 연소해석 문제에 적용해볼 예정이다.

기 호 설 명

$A N N$ : Artificial neural network

$M S E$ : Mean squared error

$R^{2}$ : Coefficient of determination

$Y$ : Mass fraction

$\dot{ω}$ : Chemical source term

Acknowledgements

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2020R1A2C2012298).

References

T. Lu, C.K. Law, Toward accommodating realistic fuel chemistry in large-scale computations, Prog. Energy Combust. Sci 35(2) (2009) 192-215. 10.1016/j.pecs.2008.10.002

U. Maas, S.B. Pope, Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space, Combust. Flame 88(3-4) (1992) 239-264. 10.1016/0010-2180(92)90034-M

J.Y. Chen, W. Kollmann, R.W. Dibble, PDF modeling of turbulent nonpremixed methane jet flames, Combust. Sci. Technol. 64(4-6) (1989) 315-346. 10.1080/00102208908924038

S.B. Pope, Computationally efficient implementation of combustion chemistry using in situ adaptive tabulation, Combust. Theory Model. 1 (1997) 41-63. 10.1080/713665229

B.A. Sen, S. Menon, Turbulent premixed flame modeling using artificial neural networks based chemical kinetics, Proc. Combust. Inst. 32(1) (2009) 1605-1611. 10.1016/j.proci.2008.05.077

A. Kempf, F. Flemming, J. Janicka, Investigation of lengthscales, scalar dissipation, and flame orientation in a piloted diffusion flame by LES, Proc. Combust. Inst. 30(1) (2005) 557-565. 10.1016/j.proci.2004.08.182

J.S. Almeida, Predictive non-linear modeling of complex data by artificial neural networks, Curr. Opin. Biotechnol. 13(1) (2002) 72-76. 10.1016/S0958-1669(02)00288-4

F.C. Christo, A.R. Masri, E.M. Nebot, Artificial neural network implementation of chemistry with PDF simulation of H₂/CO₂ flames, Combust. Flame 106(4) (1996) 406-427. 10.1016/0010-2180(95)00250-2

J.A. Blasco, N. Fueyo, C. Dopazo, J. Ballester, Modelling the temporal evolution of a reduced combustion chemical system with an artificial neural network, Combust. Flame 113(1-2) (1998) 38-52. 10.1016/S0010-2180(97)00211-3

B. Sen, E.R. Hawkes, S. Menon, Large eddy simulation of extinction and reignition with artificial neural networks based chemical kinetics, Combust. Flame 157 (2010) 566-578. 10.1016/j.combustflame.2009.11.006

B. Sen, S. Menon, Representation of chemical kinetics by artificial neural networks for large eddy simulations, 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, 2007, 5635. 10.2514/6.2007-5635

K. Wan, C. Barnaud, L. Vervisch, P. Domingo, Chemistry reduction using machine learning trained from non-premixed micro-mixing modeling: Application to DNS of a syngas turbulent oxy-flame with side-wall effects, Combust. Flame 220 (2020) 119-129. 10.1016/j.combustflame.2020.06.008

G.P. Smith, D.M. Golden, M. Frenklach, N.W. Moriarty, B. Eiteneer, M. Goldenberg, C.T. Bowman, R.K. Hanson, S. Song, W.C. Gardiner Jr., V.V. Lissianski, Z. Qin, GRI-mech 3.0, Available at: <http://www.me.berkeley.edu/gri_mech/>, 1999.

A.E. Lutz, R.J. Kee, J.F. Grcar, F.M. Rupley, OPPDIF: A fortran program for computing opposed-flow diffusion flames, No. SAND-96-8243, 1997. 10.2172/568983

J. Li, Z. Zhao, A. Kazakov, F.L. Dryer, An updated comprehensive kinetic model of hydrogen combustion, Int. J. Chem. Kinet. 36(10) (2004) 566-575. 10.1002/kin.20026

A.D. Dongare, R.R. Kharde, A.D. Kachare, Introduction to artificial neural network, Int. J. Eng. Innov. Technol. 2(1) (2012) 189-195.

L. Yu, S. Wang, K.K. Lai, An integrated data preparation scheme for neural network data analysis, IEEE Trans. Knowl. Data Eng. 18(2) (2005) 217-230. 10.1109/TKDE.2006.22

J. Wu, X.Y. Chen, H. Zhang, L.D. Xiong, H. Lei, S.H. Deng, Hyperparameter optimization for machine learning models based on Bayesian optimization, J. Electron. Sci. Technol. 17(1) (2019) 26-40.

N. Ketkar, Introduction to Keras, Deep Learning with Python, Apress, Berkeley, 2017. 10.1007/978-1-4842-2766-4

T. O'Malley, Hyperparameter tuning with Keras Tuner, 2020.

M. Uzair, N. Jamil, Effects of hidden layers on the efficiency of neural networks, 2020 IEEE 23rd International Multitopic Conference (INMIC), 2020, 1-6. 10.1109/INMIC50486.2020.9318195

A.D. Rasamoelina, F. Adjailia, P. Sincak, A review of activation function for artificial neural network, 2020 IEEE 18th World Symposium on Applied Machine Intelligence and Informatics (SAMI), 2020, 281-286. 10.1109/SAMI48414.2020.9108717

D.M. Hawkins, The problem of overfitting, J. Chem. Inf. Comput. Sci. 44(1) (2004) 1-12. 10.1021/ci034247214741005

L. Prechelt, Neural Networks: Tricks of the trade, Springer, Heidelberg, 1998.

S. Bock, M. Weiß, A proof of local convergence for the Adam optimizer, 2019 International Joint Conference on Neural Networks, 2019, 1~8. 10.1109/IJCNN.2019.8852239PMC7339648

J. Ott, M. Pritchard, N. Best, E. Linstead, M. Curcic, P. Baldi, A Fortran-Keras deep learning bridge for scientific computing, Scientific Programming, 2020. 10.1155/2020/8888811

G. Bonaccorso, Mastering machine learning algorithms: Expert techniques for implementing popular machine learning algorithms, fine-tuning your models, and understanding how they work, Packt Publishing, 2020.

Journal of The Korean Society Combustion ISSN:1226-0959(Print) 2466-2089(Online) 한국연소학회지

Preview

Artificial Neural Network for the Representation of Chemical Kinetics in Reactive Flows

ABSTRACT

MAIN

Fig. 1.

Schematic diagram of opposed-flow diffusion flame.

(1)

Fig. 2.

Overview of the artificial neural network approach.

(2)

(3)

Table 1.

ANN hyperparameter obtained by Bayesian optimization

Fig. 3.

Architecture of artificial neural network.

(6)

(7)

(8)

(9)

Table 2.

Coefficient of determination for each normalized chemical source terms with MSE

Table 3.

Coefficient of determination for each normalized chemical source terms with loss function considering the mass conservation of elemental species

Fig. 4.

Comparison of the ANN predictions on normalized chemical source terms of the 8 species against the normalized target values for the testing database unseen during training with MSE.

Fig. 5.

Comparison of the ANN predictions on normalized chemical source terms of the 8 species against the normalized target values for the testing database unseen during training with loss function considering the mass conservation of elemental species.

Fig. 6.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 1,055 s-1.

Fig. 7.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 5,550 s-1.

Fig. 8.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 10,955 s-1.

Table 4.

MSE between chemical source terms obtained by CKWYP-ANN and CKWYP at the different global strain rates

Fig. 9.

Speed-up between CKWYP and CKWYP- ANN for GRI-Mech 3.0.

Fig. 10.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 1,055 s-1: (a) H2 mass fraction (b) OH mass fraction (c) H2O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Fig. 11.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 5,550 s-1: (a) H2 mass fraction (b) OH mass fraction (c) H2O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Fig. 12.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 10,955 s-1: (a) H2 mass fraction (b) OH mass fraction (c) H2O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Table 5.

MSE between target values obtained by OPPDIF-ANN and OPPDIF at the different global strain rates

Acknowledgements

References

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 1,055 s^-1.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 5,550 s^-1.

Chemical source terms obtained by CKWYP and CKWYP-ANN at the global strain rate = 10,955 s^-1.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 1,055 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 5,550 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.

Target values obtained by OPPDIF and OPPDIF- ANN at the global strain rate 10,955 s^-1: (a) H₂ mass fraction (b) OH mass fraction (c) H₂O mass fraction (d) Temperature as a function of distance from fuel nozzle.