1. 서 론
2. 방법론
2.1 실험 장비, 계측 방법 및 운용 조건
2.2 3차원 유한요소법 기반 고유치 해석
3. 실험 결과 및 고찰
3.1 고유치 해석 결과
3.2 방위 방향 불안정의 발생 메커니즘
4. 결 론
1. 서 론
희박 예혼합 연소 방식이 적용된 가스터빈 연소기는 요구되는 출력을 만족하면서도, 현재 강력히 규제되고 있는 NOx 및 CO와 같은 유해 가스 발생량을 감소시켰다. 하지만 희박 가연 한계에 가까운 당량비 조건으로 인해 연소기 내부의 화염은 작은 섭동에도 불안정하게 되었다. 연소기의 고유주파수에 결합해 큰 진동과 소음을 유발하는 연소불안정 현상을 규명하기 위해, 그간 학계에서 수치 및 실험적 연구가 활발하게 수행되었다[1,2,3,4,5,6]. Lieuwen과 Neumeier[1]은 압력 섭동과 화염의 열 방출률 섭동 사이의 관계가 자발 불안정 발생에 중요한 요인임을 실험적으로 규명했다. Kim[3]은 다양한 운용 조건에서 계측된 많은 수의 데이터를 이용하여, 압력 및 열 방출률 섭동 간의 위상 차이가 90도 이내의 정위상 관계일 때 연소불안정이 나타남을 보였다. 이의 데이터를 벤치마킹하여 Cha 등[4]은 OSCILOS를 통한 예측 결과를 실험적으로 계측된 결과와 비교하였다. Shin 등[5]은 헬름홀츠 방정식을 이용한 모드 해석 및 대와류해석 기법을 통해 연소불안정을 예측하였다.
최근에는 탄소중립 동향에 발맞춰 수소 가스터빈 연소기술에 대한 관심이 모이고 있다[7]. 이에 따라 저·고농도 수소 혼소 또는 수소 전소 환경에서 나타나는 연소불안정에 대한 다양한 연구가 국내외에서 진행되고 있다[8,9,10,11,12]. 예를 들어 Baraiya와 Chakravarthy[8]는 블러프 바디(bluff body) 연소기에서 수소 혼소 및 전소 실험을 수행하여 연료 다변화에 따른 연소불안정 거동을 확인했다. Lee와 Kim[9,10]은 메조스케일 다중노즐 배열에서 예혼합 수소 화염의 구조와 동특성을 보고했다. 특히, 순수 수소 화염은 메탄 화염과는 달리 높은 차수의 길이 방향 모드와 결합함을 확인했다. Yoon 등[11]은 수소 전소 조건을 포함한 다양한 연료 조성에서 실험하여, 수소 함량이 증가함에 따라 불안정 주파수는 고조파(higher harmonics)로 천이함을 보고했다. 동일한 실험 장비로 Joo 등[12]은 연료 분사의 위치가 연소 동특성에 미치는 영향을 파악하였고, 이를 3차원 유한요소법 기반의 음향 해석 결과와 비교하였다.
이처럼 많은 연구 그룹들이 가스터빈 연소기에 치명적인 손상을 야기하는 불안정성을 제어하기 위해 단일 노즐 및 단일 연소기에 초점을 두어 다양한 연구를 진행해왔다. 하지만 이러한 연소 환경은 화염 간의 상호작용 및 인접 연소기 간의 음향 상호작용이 필연적으로 발생하는 캔-환형 구조의 연소 환경과 차이가 있다. 주로 발전용 가스터빈 연소기에 채택되는 캔-환형 구조는 원주 방향으로 이루어진 짝수 개의 연소기로 구성된다. 이때 터빈 1단 노즐 상류에서 인접한 연소기들을 연결하는 크로스톡(cross-talk) 영역이 존재하여, 연소기 간에 음향 상호작용이 발생한다[13]. 독특한 음향 환경을 갖는 캔-환형 연소기의 동특성을 분석하기 위한 연구가 점차 주목받고 있다[14,15,16,17,18,19,20,21]. 수치적인 예로 Ghirardo 등[14]은 14개로 구성된 캔-환형 연소기 시스템을 해석하여 음향 상호작용 모드가 축 방향 및 방위 방향 모드 형태로 나타남을 확인했다. 최근 Yoon [15]은 저차 음향 모델과 3차원 유한요소법을 이용해 다중 연소기 시스템의 상호작용 패턴 및 상응하는 모드 형상에 대해 분석했다. 실험적인 연구로 Moon 등[16]은 대칭 및 비대칭 입구 조건에서 발생하는 불안정 모드를 분석하여 인접 연소기가 정위상으로 진동하는 푸시-푸시(push-push) 모드와 역위상으로 진동하는 푸시-풀(push-pull) 모드의 존재를 규명했다. 이를 확장한 연구로 Moon 등[19,20,21]은 다양한 운용 조건에서 환형 크로스톡 영역으로 연결된 사중 캔-환형 연소기를 실험했다. 특히 이들은 모드 군집화(mode clustering), 모드 국소화(mode localization), 그리고 고유치 축퇴(eigenvalue degeneracy)를 포함한 주요 현상들이 캔-환형 연소기 구조에 지배적으로 나타남을 밝혔다.
본 연구에서는 동일한 사중 캔-환형 연소기에서 야기된 방위 방향 자발 불안정 모드에 초점을 두어 이의 발생 메커니즘을 연구하였다. 이때 선행 연구[22]를 참고하여 높은 주파수의 음향섭동을 발생시키는 수소 전소 예혼합 화염을 이용했다. 더불어 3차원 유한요소법 기반의 헬름홀츠 솔버(Helmholtz solver)를 이용해 주파수 영역에서 존재하는 음향 상호작용 모드의 패턴과 상응하는 형상을 계산하였고, 이를 실험 결과와 비교하였다. 마지막으로 파동분해기법(acoustic wave decomposition method)을 포함한 다양한 분석 기법을 주요 신호들에 적용하여 캔-환형 모드 동특성을 면밀히 파악했다.
2. 방법론
2.1 실험 장비, 계측 방법 및 운용 조건
Fig. 1(a)는 본 실험에 사용된 사중 예혼합 연소기를 나타낸 그림이다. 캔-환형 연소기 구조에서 나타나는 동특성을 실험적으로 분석하기 위해 제작된 이 장비는 네 개의 동일한 연소기로 구성되어 있으며, 각 연소기는 하류에서 완전한 환형 형상으로 이루어진 크로스톡 영역으로 연결된다. 연소기 상류로부터 멀리 떨어진 위치에서 순도 99.999%의 수소(H2)를 주입하여 완전 예혼합 조건을 달성하였다. 음향학적으로 닫힌 경계조건을 형성하기 위해서 노즐 상류에는 초크 플레이트가 설치되어 있고 하류에는 막힘률 80.5%의 피스톤이 설치되어 있다. 이때 피스톤은 연소기 내부에서 길이 방향으로 조절 가능하며, 덤프면에서 피스톤 헤드까지의 길이로 정의되는 연소기 길이를 900에서 1800 mm까지 변화시킬 수 있다. 실험에 사용한 노즐의 단면도를 Fig. 1(b)에 도시했다. 노즐 어셈블리는 총 97개의 다중 노즐 인젝터로 구성되어 있으며, 개별 노즐의 직경은 3.0 mm로 동일하다. 이때 직경의 편차는 0.05 mm이다. 해당 노즐 구조는 선행 연구 결과[22]를 바탕으로 설계되었으며, 반응속도가 매우 높은 수소 화염을 안정적으로 제어하기 위해 하나의 큰 화염장을 많은 수의 작은 화염으로 대체한 형상을 갖는다. 복잡한 캔-환형 연소기의 동특성을 분석하기 위해, 총 20개의 동압 센서(PCB piezotronics, 112A22)를 설치하였다. Fig. 1(a)에 도시하였듯, 이러한 동압 센서들은 연소기의 길이 방향( 그리고 ) 및 크로스톡 영역의 방위 방향()에 설치된다. 이때 하첨자 는 연소기의 번호이다. 또한, 화염 동특성의 정량적인 계측을 위해 광증배관(PMT, Hamamatsu model H7732-10)를 이용하여 OH* 자발광을 계측하였고, 이를 열 방출률 섭동()의 척도로 사용하였다.
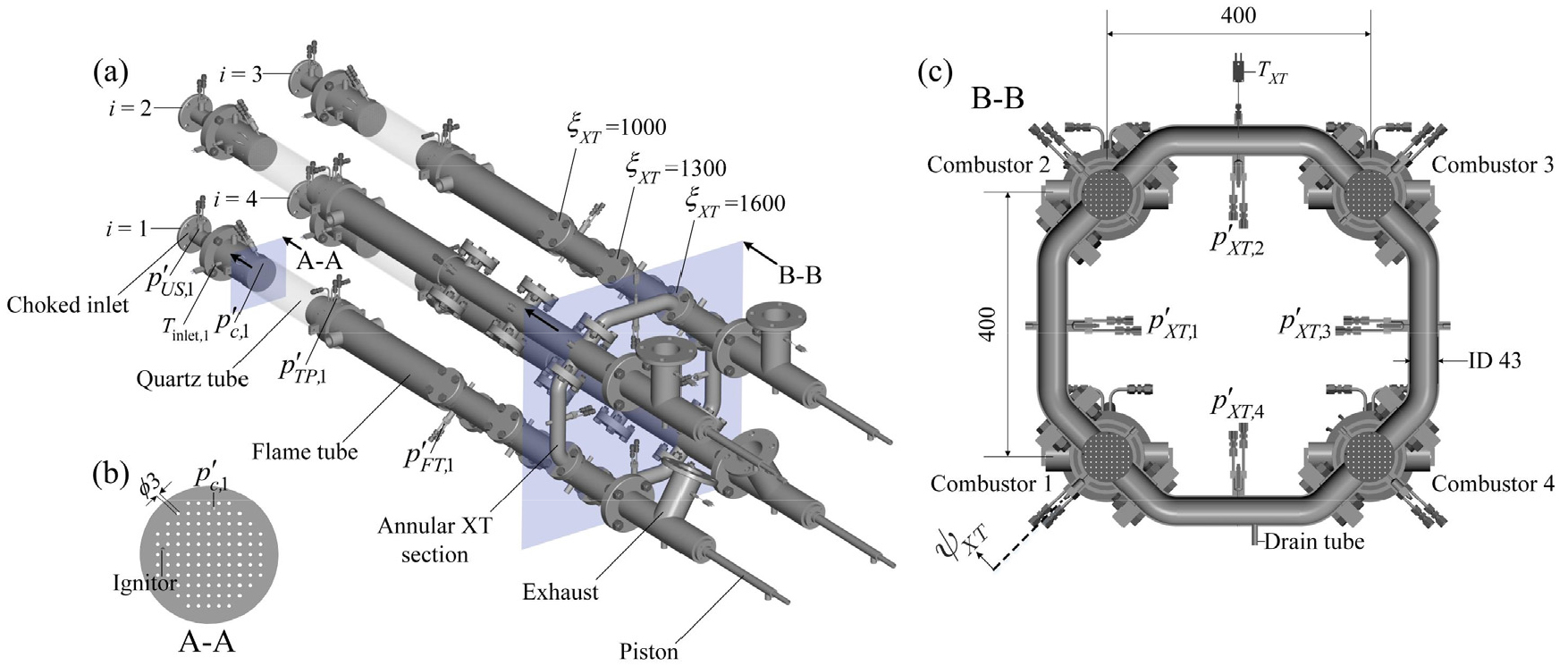
Fig. 1.
(a) Four lean-premixed tunable combustors equipped with small-scale multi-element injectors. (b) Spatial arrangements of multi-element injectors consisting of a total of 97 nozzles (A-A plane). (c) Cross-sectional view of annular cross-talk section (B-B plane). Circumferential coordinate for annular cross-talk section () is defined with respect to the centerline of Combustor 1 in clockwise direction. = pressure transducers, = thermocouples, US = upstream, TP = transition piece, FT = flame tube, XT = cross-talk, ID = inner diameter. Dimensions in millimeters.
Fig. 1(c)는 환형 크로스톡 영역의 단면도를 나타낸 그림이다. 본 실험에서는 두 연소기 간의 거리(400 mm)와 크로스톡의 내경(43 mm)은 일정하게 두었다. 크로스톡 영역 내부의 압력 섭동을 계측하기 위해 네 개의 동압 센서를 90도 간격으로 배치했고, 인접한 연소기들의 중앙에 위치하도록 설치했다. 더욱 자세한 실험 장비의 설명은 [19]에서 다루었다.
마지막으로, 본 연구에서 고려한 실험 조건은 다음과 같다. 완전 예혼합된 수소-공기 혼합물을 200±5 ℃로 예열하여 모든 노즐에 30±1 m/s의 평균 유속으로 공급했다. 반응물의 당량비는 0.52로, 단열화염온도로는 1813 K에 해당하며 모든 연소기가 동일한 당량비를 갖도록 설정했다. 이때 계산된 당량비의 불확실성은 대략 1.5%이다. 또한 크로스톡 영역의 위치는 1300 mm로, 연소기 길이와 크로스톡 영역의 원둘레가 유사한 크기를 갖는 조건에서 실험하였다. 해당 조건에서 시스템이 정상상태로 진동할 때, 모든 압력 및 열 방출률 섭동 신호를 24 kHz 샘플링 주파수로 4초간 획득하였다.
2.2 3차원 유한요소법 기반 고유치 해석
본 연구에서는 COMSOL Multiphysics 시뮬레이션 소프트웨어를 이용해 3차원 유한요소법 기반의 고유치 해석을 진행하였다. 복잡한 형상의 캔-환형 연소기를 공간적으로 이산화하여 대략 11,500,000개의 요소로 구성했고, 이를 헬름홀츠 솔버로 해석하여 실험 결과와 비교하였다. 이때 연소기의 입구와 출구 도메인의 음향 경계는 닫힌 조건으로 설정했다. 더불어 입구부의 온도는 연료-공기 혼합물의 온도와 동일하게 설정하였고, 주어진 당량비 조건에서 연소 생성물 온도는 이전에 계측된 단일 연소기의 주파수 결과를 바탕으로 도출하였다[19]. Fig. 1(c)에 표시한 크로스톡 영역에서의 온도()를 직접 열전대로 계측하여 해당 도메인의 열역학적 상태량으로 이용했다. 마지막으로 화염의 정보인 화염전달함수(flame transfer function) 혹은 화염묘사함수(flame describing function)를 해석에서 제외하여 시스템의 고유 모드 및 상응하는 모드 형상 정보만 분석에 활용했다.
3. 실험 결과 및 고찰
3.1 고유치 해석 결과
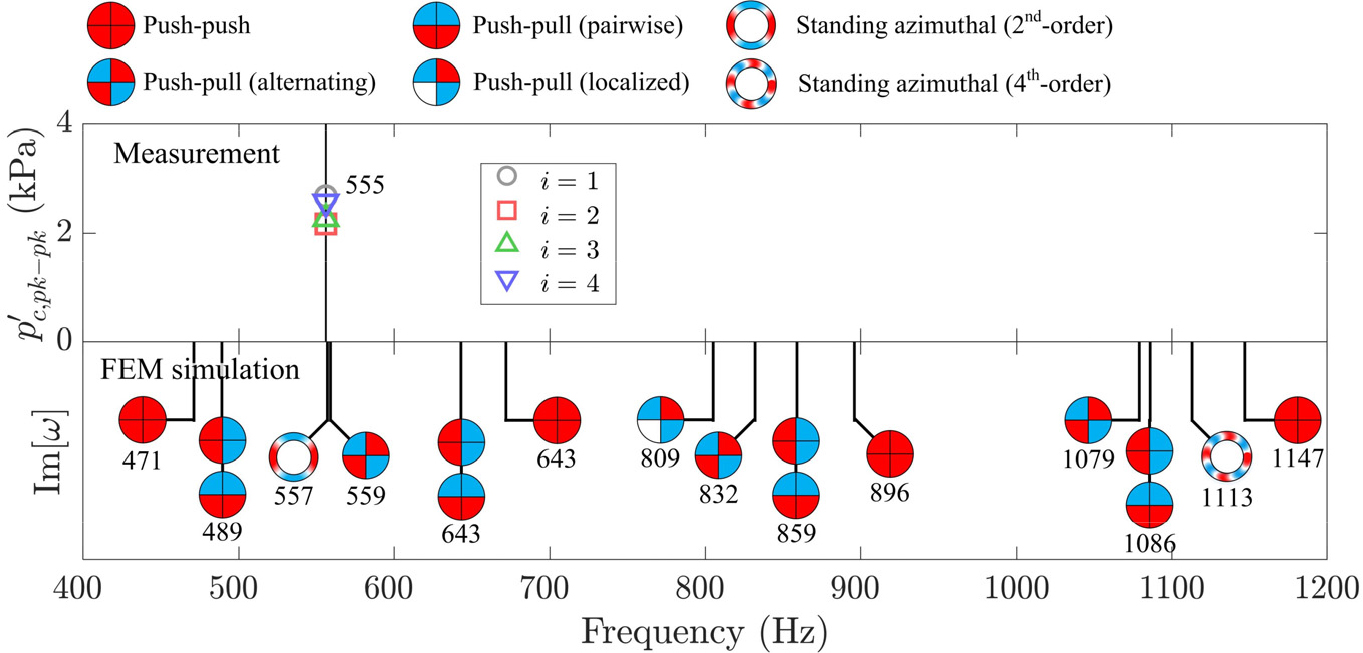
Fig. 2는 주파수 영역에서 도출된 실험 결과와 유한요소법 기반의 고유치 해석 결과를 보여준다. 이때 계산된 고유 모드의 상호작용 패턴을 직관적으로 나타내기 위해 사등분으로 나뉜 심볼을 사용했고, 연소기 간의 위상 관계를 색깔로 구분했다. 다양한 상호작용 형태를 보이는 총 18개의 고유 모드가 400-1200 Hz 범위에 존재하며, 군집하는 모습을 보인다. 길이 방향 모드는 네 개의 연소기가 정위상으로 진동하는 푸시-푸시 모드, 인접 연소기들이 역위상으로 진동하는 푸시-풀 모드, 짝을 지어 역위상으로 진동하는 푸시-풀 모드, 그리고 국소화된 푸시-풀 모드 패턴으로 나타나고, 방위 방향 모드는 2차 및 4차 정상파 모드 형태로 나타났다. 이때 방위 방향 모드는 환형 크로스톡 영역에만 국소화되며, 네 개의 연소기 영역에서는 압력 노드가 형성된다. 고주파 영역에 존재하는 길이 방향 및 방위 방향 모드의 동특성은 이전 선행연구에서 자세하게 다루었다[21]. Fig. 2에서 계측된 실험 결과를 보면 사중 캔-환형 연소기는 555 Hz에서 불안정했다. 중요한 점은 실제 실험 결과 근처에 2차 방위 방향 모드(557 Hz)와 인접 연소기들이 역위상으로 진동하는 길이 방향 푸시-풀 모드(559 Hz)가 계산된다는 점이다. 해당하는 두 개의 고유 모드는 엄연히 다른 고유 상태를 갖지만, 매우 인접한 고유치에서 공존한다. 이와 같이 하나의 고유 주파수에 두 개 이상의 고유 벡터가 존재하는 현상을 고유치 축퇴라 일컫는다[23,24]. 다음 절에서는 크로스톡 영역과 연소기 영역에서 계측된 주요 신호들을 다양한 분석 기법을 이용하여 분석하였다.
3.2 방위 방향 불안정의 발생 메커니즘
Fig. 3(a)는 환형 크로스톡 영역의 압력 신호()에 대한 시계열 결과이다. 확연하게 1번 압력 신호는 3번 신호와 정위상 관계에 있지만, 2번 및 4번 신호와는 전체적으로 역위상 관계를 보이며 정상파 거동을 보인다. 푸리에 변환으로 계산된 불안정 주파수는 555 Hz로 크로스톡 영역은 하나의 지배적인 주파수에서 진동한다. 불안정 모드의 동특성을 엄밀히 분석하기 위해 파동분해기법을 이용하였다[25,26]. 원주 방향으로 전파되는 압력파는 식 (1)과 같이 시계 방향 및 반시계 방향의 두 음파의 합으로 표현된다.
여기서 와 는 시계 및 반시계 방향의 복소 진폭, 은 방위 방향 모드의 차수, 는 압력 센서의 계측 위치이고 는 복소 각진동수이다. Fig. 3(a)에 두 음파의 성분으로 재구성된 신호들을 심볼로 나타냈다. 재구성된 네 개의 압력 신호들이 실험에서 계측된 시계열 결과와 일치하며, 식 (1)과 같이 수치적으로 분해된 압력파에 큰 오차가 없음을 확인했다.
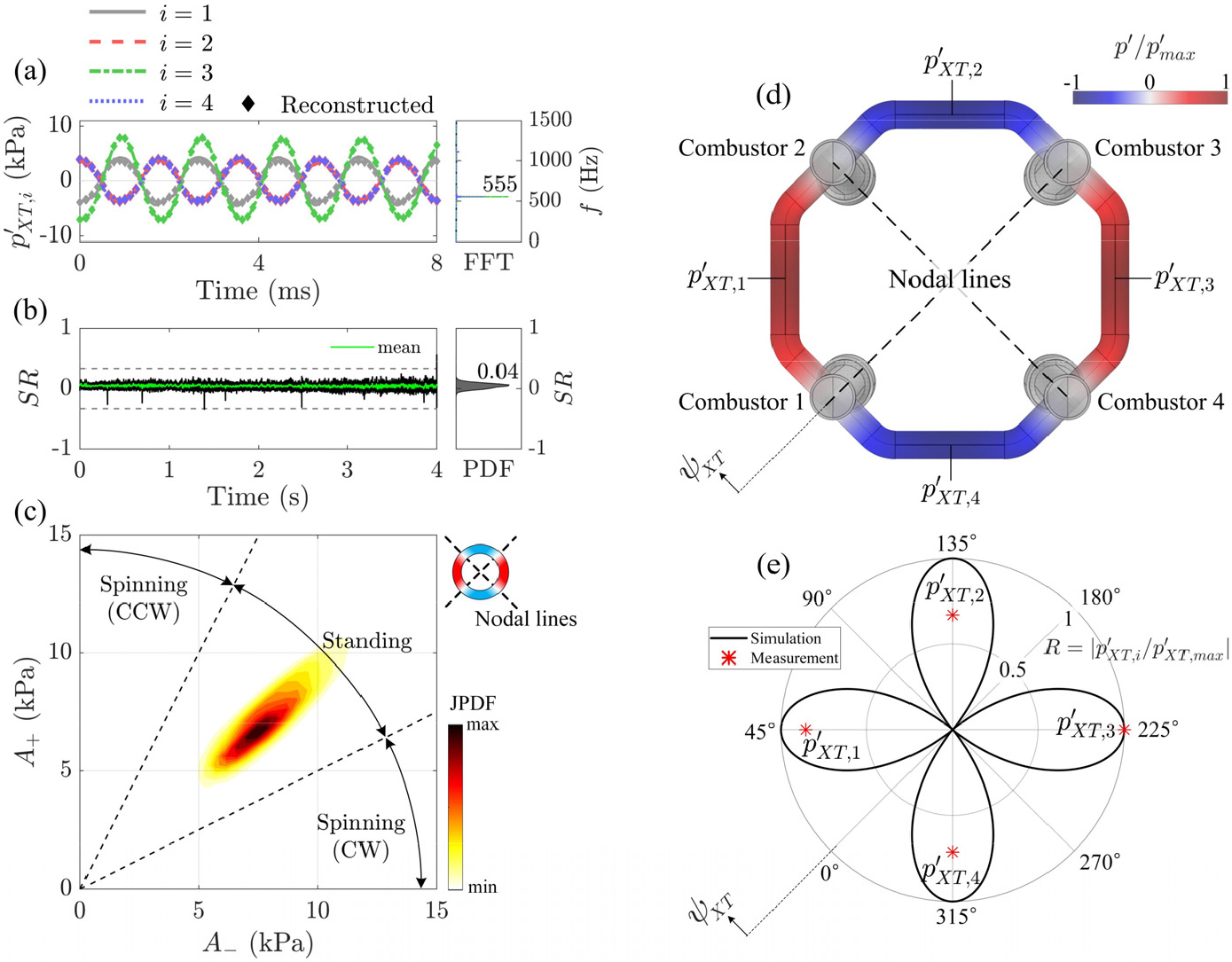
Fig. 3.
(a) Time traces of four pressure signals in annular cross-talk section and corresponding fast Fourier transform (b) Temporal variation of spin ratio and corresponding probability density function. Dashed lines indicate threshold values for quantitative evaluation of spinning or standing mode. (c) Joint probability density functions of the amplitude of two waves traveling in clockwise () and counter-clockwise directions (). Clockwise and counter-clockwise directions are denoted as CW and CCW. (d) 3D modal structure of second-order standing azimuthal eigenmode. (e) Mode shape in annular cross-talk section expressed in polar coordinates: solid line – FEM simulation, symbols – measurements.
분해된 두 개의 복소 진폭을 이용하여 방위 방향 불안정 모드의 동특성을 구분할 수 있다. 만약 일 경우, 완전한 정상파 모드이고, 이면 시계 방향 회전 모드 그리고 이면 반시계 방향 회전 모드이다. 이때 정량적으로 방위 방향 모드의 동특성을 구분하기 위해 식 (2)로 표현되는 회전비(spin ratio)를 사용한다[27].
이면 완전한 정상파 모드이고, 이면 완전한 회전 모드이다. 이전 참고 문헌에서는 회전비 값의 경계를 두어 시스템에 나타나는 지배적인 모드를 판별했다[25,28]. 일 경우, 정상파 모드가 지배적으로 나타나는 동특성을 갖고 및 인 경우에는 회전 모드의 동특성이 지배적이다.
Fig. 3(b)는 시간에 따른 회전비와 이의 확률 밀도함수를 보여준다. 이때 두 파선은 정상파 및 회전 모드를 구분 짓는 경계선이다. 확연하게 회전비가 경계선 내에 있고 이의 평균값이 0.04이므로, 환형 크로스톡 영역에서 정상파 모드가 야기되었음을 알 수 있다. 두 음파의 진폭에 대한 결합확률분포를 나타내는 Fig. 3(c)가 이러한 주장을 뒷받침한다. 더불어 Fig 3(a)에 도시한 크로스톡 압력 신호 간 위상 관계를 통해 해당 동역학적 상태가 2차 정상파 불안정 모드()임을 알 수 있다. 다음으로 계측된 실험 결과를 유한요소법으로 계산된 557 Hz의 2차 방위 방향 모드와 비교하였다. Fig. 3(e)는 극좌표에서 표현한 모드 형상 결과이다. 여기서 반지름은 최댓값으로 정규화된 압력 섭동의 진폭이고 방위각은 1번 연소기의 중심선을 기준으로 한 크로스톡 영역의 원주방향 좌표()이다. 네 개의 크로스톡 위치에서 압력 안티노드 조건이 형성되며 실험 결과와 부합함을 보여준다. 이때 3번 신호만 다소 큰 진폭을 보이는데, 이는 시뮬레이션에서 화염 동특성의 정량적인 정보인 화염전달함수 혹은 화염묘사함수를 포함하지 않았기 때문이다. 중요한 점은 2차 방위 방향 모드의 마디선(nodal line)들이 연소기 부분에서 형성된다는 점이다. Fig. 3(d)에 도시한 3차원 모드 형상 정보에서도 확인할 수 있듯, 음향섭동을 만드는 화염이 위치한 연소기 챔버 영역에서 압력 노드 조건이 형성되고, 화염의 위치에서 다소 떨어진 크로스톡 영역에서만 정규화된 압력 진폭을 갖는다. 즉 환형 크로스톡 영역의 방위 방향 모드는 독립적으로 발생할 수 없고, 이를 야기하는 압력 섭동 에너지는 다른 불안정 모드로 인해 공급되었음을 유추할 수 있다.
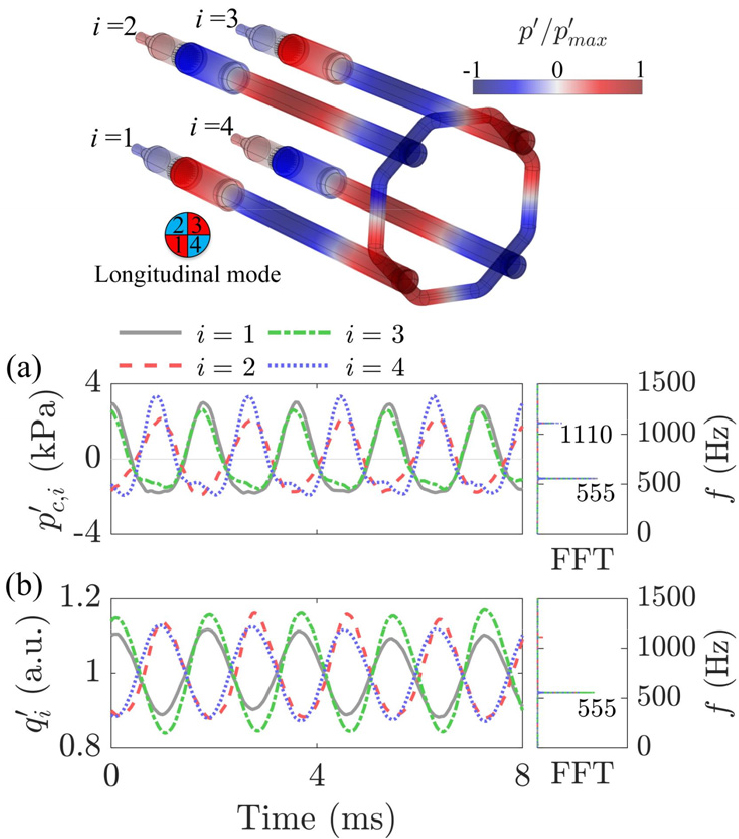
방위 방향 모드를 야기하는 물리적인 메커니즘을 이해하기 위해 연소기 챔버에서 발생한 주요 신호들을 분석했다. Fig. 4에 연소기 챔버의 압력() 및 화염의 열 방출률 섭동()에 대한 시계열 결과와 이에 상응하는 3차원 모드 형상을 나타냈다. 인접한 연소기들은 역위상 관계로 진동하고, 기본 주파수는 크로스톡 영역의 결과와 같은 555 Hz이다. 한편 연소기 챔버 압력 섭동은 기본 주파수 이외에 2차 조화파의 진폭도 강하게 나타난다. 고조파가 두드러지게 발생하는 군집 수소 화염의 동특성은 이전 선행 연구에서 분석된 바 있다[22]. 이와 같은 결과로 연소기 부분에서는 Fig. 4에 도시한 3차원 모드 형상과 같은 길이 방향 모드(Fig. 2에 나타낸 559 Hz의 고유 모드)가 야기되었음을 알 수 있다. 이는 실험 결과 근처에 존재하는 축퇴된 두 개의 고유 모드가 동시에 증폭되었음을 의미한다.
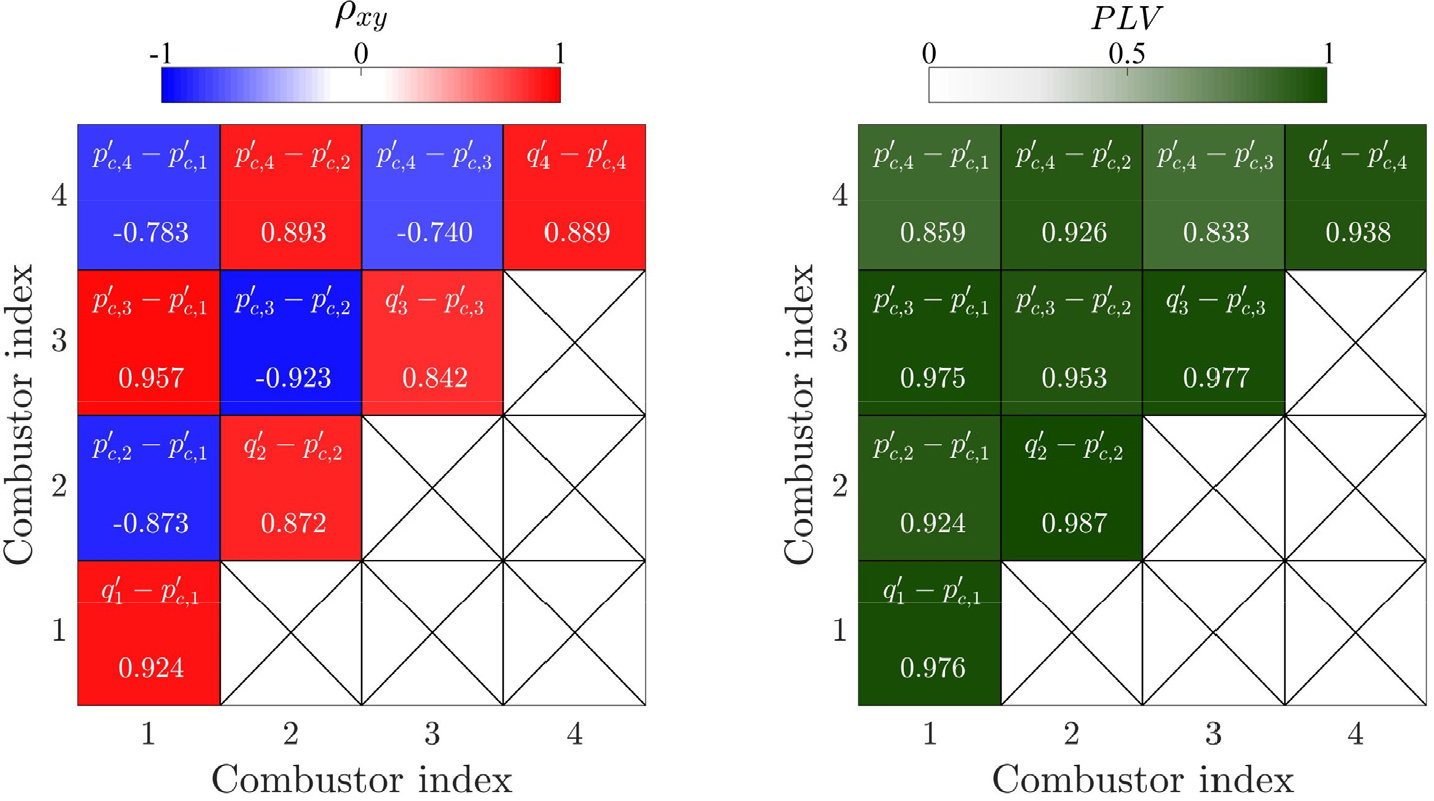
Fig. 5는 주요 신호 간 상관계수(correlation coefficient)와 위상 고정값( : phase locking value)에 대한 행렬이다. 행렬의 대각선 원소는 각 연소기의 화염과 음향장 사이의 상호작용 결과이고, 대각선이 아닌 원소는 연소기 간의 음향 상호작용 결과를 보여준다. 이때 상관계수는 Pearson[29]이 제안한 방법론을 이용하여 계산했고, 식 (3)과 같이 계산된다.
여기서 는 상관계수, 는 주요 신호, 은 데이터 개수, 그리고 𝜇와 𝜎는 각각 변수의 평균값과 표준편차이다. 는 -1부터 1 사이의 값을 가지며 인 경우엔 두 신호 사이에 양의 상관관계가 있고, 인 경우는 음의 상관관계가 있음을 의미한다.
는 식 (4)와 같이 표현되며 두 신호가 동조한 정도를 정량적으로 나타낸다[30].
이때 는 두 신호 간의 순간 위상차이다. 는 0부터 1 사이의 값을 갖고, 1에 가까울수록 두 신호가 동조됨을 의미한다.
우선 상관계수 행렬을 보면, 대각선 원소 모두 양의 값(0.842~0.924)을 가지므로 연소기 내의 화염과 음향장 사이에 강한 비례 관계가 있음을 보여준다. 상응하는 도 1에 가까우므로 화염의 열 방출률 섭동과 연소기 압력 섭동 사이에 완전한 동조 관계가 성립되었다. 이러한 결과들은 불안정이 발생하기 위한 필요조건인 레일리 기준(Rayleigh criterion)이 만족되어, 전체 시스템에 섭동 에너지가 공급되었음을 보여준다[31]. 더불어 대각선이 아닌 원소들로 인접 연소기 간에 역위상 관계가 있는 푸시-풀 모드임을 다시 확인할 수 있다. 결과적으로 레일리 기준을 만족하는 연소기에서 섭동 에너지가 공급되어 전체 연소기는 길이 방향 모드로 불안정하게 되었고, 이로 인해 크로스톡 위치에 음향섭동이 전달되어 방위 방향 불안정 모드가 야기될 수 있음을 보여준다. 이로써 캔-환형 연소기의 방위 방향 불안정이 발생되는 물리적인 메커니즘은 고유치 축퇴 현상과 관련되어 있음을 보였고, 독립적으로 발생할 수 없는 방위 방향 모드는 화염에 의해 증폭된 길이 방향 모드와 함께 발생됨을 실험적으로 보였다.
4. 결 론
캔-환형 구조에서 필연적으로 나타나는 연소기 간의 음향 상호작용은 불안정 발생의 주요 인자임에도 불구하고, 현재까지 관련된 연구는 단일 연소기에 국한되어 있었다. 본 연구에서는 캔-환형 연소기 구조에서 나타난 방위 방향 불안정의 거동과 이러한 모드를 야기하는 물리적인 메커니즘을 실험적으로 연구하였다. 더불어 3차원 유한요소법을 이용한 음향 모드 시뮬레이션을 수행하여 이를 계측된 데이터와 비교하였다. 파동분해기법으로 분석된 신호를 통해 환형 크로스톡 영역은 2차 방위 방향 모드 형태로 불안정함을 보였고, 해당 고유 모드를 불안정하게 하는 섭동 에너지는 동일한 주파수에 존재하는 축퇴된 길이 방향 푸시-풀 모드가 화염에 의해 증폭되면서 하류의 환형 영역으로 공급됨을 확인하였다. 따라서 연소기 영역에서 나타난 길이 방향 모드와 환형 크로스톡 영역에서 나타난 방위 방향 모드가 동시에 야기되면서, 전체 시스템은 복잡한 동적 특성을 보였다.