1. 서 론
2. 메커니즘 축소 연구 방법
2.1. 오차전달법(DRGEP)
2.2. 바이오디젤 화학반응 메커니즘
2.3. 메커니즘 자동 축소화
2.4. 메커니즘 축소 환경 및 표적 화학종
3. 결과 및 고찰
3.1. 메커니즘 합성
3.2. 메커니즘 축소 환경 설정
3.3. 표적 화학종 변화에 따른 영향
4. 결 론
1. 서 론
탄화수소 연료의 복잡한 연소 현상을 수치 해석적으로 모사 및 예측하기 위해서는 탄화수소 연료의 화학반응 메커니즘이 필요하며, 현재까지 다양한 종류의 탄화수소 연료에 대한 상세화학반응 메커니즘이 제시되었다[1], [2], [3]. 하지만, 상세화학반응 메커니즘은 수많은 화학종과 반응식을 포함하고 있어 3차원 CFD(Computational Fluid Dynamics) 또는 복잡한 계산이 필요한 수치 해석 모델에 상세화학반응 메커니즘을 적용할 경우, 계산 부하 및 발산 문제를 초래하기 때문에 연소 해석을 수행함에 있어서 많은 어려움을 가져온다. 특히, 함산소 연료인 바이오디젤을 모사한 상세화학반응 메커니즘[1]은 실제 바이오디젤의 구성 요소인 FAME(Fatty Acid Methyl Esters)의 이중결합 특성을 대체 화학종을 통해 성공적으로 모사하였으나, FAME의 긴 탄소결합의 화학구조와 복잡한 분자구조로 인해 다른 모사 연료의 상세화학반응 메커니즘보다 많은 3,299개의 화학종과 10,806개의 반응식으로 구성되었다. 이로 인해 바이오디젤 화학반응 메커니즘이 적용된 3차원 CFD를 통한 연소 해석 연구에 많은 어려움이 따른다[4].
이러한 문제를 해결하기 위해서 많은 연구자들은 상세화학반응 메커니즘을 축소하기 위한 다양한 방법들[5], [6], [7], [8], [9], [10]을 제시하였고, 이러한 방법들 중에 Lu 등[11]이 제시한 직접 관계 그래프(Directed Relation Graph, DRG) 방법이 많이 적용되고 있다. DRG 방법은 메커니즘에 포함된 화학종 사이의 영향을 Mapping한 상호 관계 그래프를 적용하고, 사용자가 설정한 표적(Target) 화학종과 경계 값(Threshold, ε)으로 불필요한 화학종 및 반응식을 효과적으로 제거하는 방법이다. 하지만, DRG 방법은 표적 화학종이 보존되도록 설정되어 표적 화학종과 관련된 모든 화학종이 메커니즘 내에 제거되지 않고 유지되기 때문에 메커니즘 축소율이 낮아지는 단점을 가지고 있다. 이를 위해 Pepiot-Desjardins 등[12]은 표적 화학종과 이와 관련된 화학종 사이의 경로에 대한 오차를 고려하여 DRG 방법의 단점을 보완하는 오차전달법(Error Propagation, DRGEP)을 제시하였다. 또한, Niemeyer 등[13]은 DRGEP 방법을 기반으로 민감도 조사법(Sensitivitiy analysis)을 추가하여 DRGEPSA 방법을 제시하였다.
이러한 방법들을 바탕으로 본 연구에서는 바이오디젤 상세화학반응 메커니즘을 사용하여 3차원 CFD에 적용할 수 있는 바이오디젤 축소 메커니즘의 개발을 목표하고 있다. 이를 위해 선행 연구[14]에서는 DRGEP 방법을 적용하여 메커니즘 축소 환경을 다양하게 변화시켜 그에 따른 영향을 확인하고, 가장 적절한 기초화학반응 메커니즘을 생성하였다. 하지만, 사용된 바이오디젤 상세화학반응 메커니즘에는 질소산화물(Nitrogen oxide, NOX) 및 그을음(Soot) 관련 화학종에 대한 메커니즘을 포함하고 있지 않기 때문에 표적 화학종 선택에 제한이 있었으며, 이로 인해 표적 화학종의 변화에 따른 영향을 파악하지 못했다. DRGEP 방법에서 표적 화학종의 중요성은 표적 화학종과 관련된 화학종 사이의 경로에 대한 오차를 고려하기 때문에 나타난다. 하지만, DRGEP 방법 및 이를 기반으로 한 축소 방법을 사용한 연구에서는 각 연구마다 표적 화학종의 설정이 다르고, 표적 화학종 변화에 따른 메커니즘 축소에 미치는 영향에 대한 연구가 미흡하다고 판단된다[15], [16].
따라서, 본 연구는 표적 화학종 변화에 따른 축소 메커니즘 변화에 대한 연구를 위해 선행 연구[14]를 통해 생성된 기초화학반응 메커니즘과 NOX 및 Soot 관련 화학종이 포함된 n-heptane 메커니즘을 합성하여 다양한 표적 화학종에 대한 차이를 메커니즘 축소율 및 점화지연 오차율을 통해 비교 분석하였다.
2. 메커니즘 축소 연구 방법
2.1. 오차전달법(DRGEP)
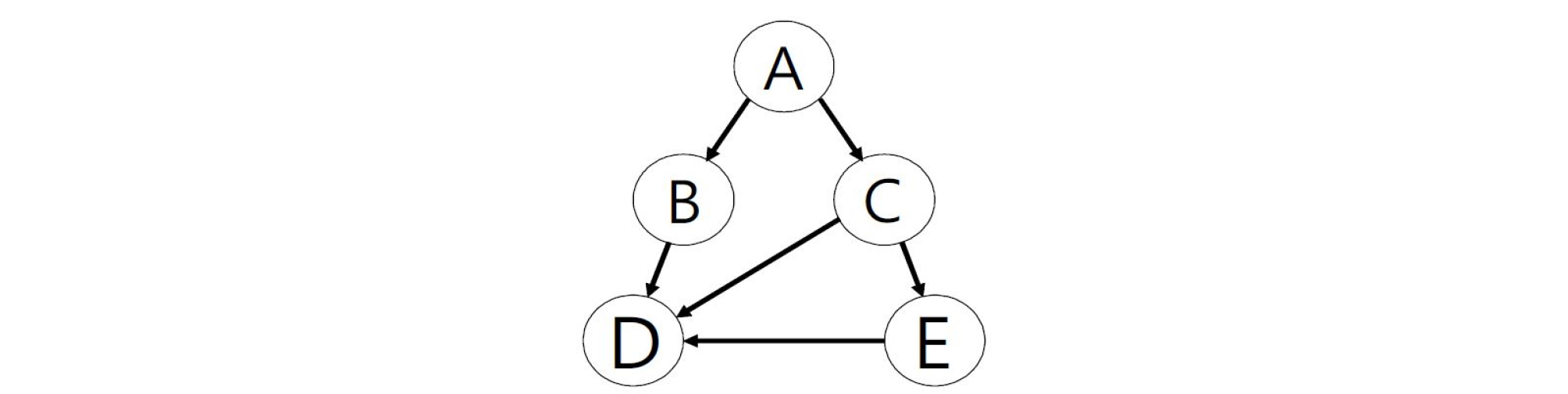
DRGEP 방법은 DRG 방법을 기반으로 오차전달법을 적용한 방법이다. DRG 방법은 메커니즘 축소를 위한 분위기 조건(분위기 온도, 압력 및 당량비) 및 표적 화학종의 설정을 통해 화학종들의 생성률을 계산하여 중요하지 않은 화학종을 제거할 수 있도록 고안된 방법이다. DRG 방법은 Fig. 1과 같이, 직접 관계 그래프를 통해 메커니즘 내에서 각각의 화학종들 사이의 관계로 표현 가능하다. 여기서, 화학종 A의 생성률은 화학종 A와 관련된 모든 화학반응의 진행 속도 변수의 총합으로 나타낼 수 있다.
| $$R_A=\sum_{i=1}^Iv_{A,i}W_i$$ | (1) |
또한, 아래첨자 i와 A는 i번째 화학반응 과정과 화학종 A를 의미한다. vA,i는 화학종 A의 이론 반응 계수이며, wi는 i번째 화학반응에 대한 진행 속도 변수이다. 이러한 식 (1)을 사용하여 화학종 A와 화학종 B의 관계를 식 (2)와 같이 나타낼 수 있다.
| $$r_{AB}=\frac{\sum\left|v_{A,i}w_i\delta_{B,i}\right|}{V_{A,i}w_i}$$ | (2) |
위의 식 (2)에서 화학종 B가 i번째 화학반응에 관여한다면, δB,i는 1이 되고, 관여하지 않는 경우에는 0이 된다. 이러한 방법으로 화학종 A에 대한 화학종 B의 의존도를 확인하기 위해 임의의 경계 값(ε)을 사용자가 정의한다. 만약 rAB값이 ε보다 작다면, 화학종 A에 대한 반응식에서 화학종 B의 의존도가 낮다고 판단되어 화학종 B는 제거된다.
오차전달법(DRGEP)은 DRG 방법에 식 (3)과 (4)를 추가하여 화학종 사이의 경로에 대한 오차를 고려 가능하도록 나타낼 수 있다.
| $$r_{AB,p}=\prod_{i=1}^{n-1}r_{S_jS_{j+1}}$$ | (3) |
| $$R_{AB}=\max\nolimits_{all\;paths\;p}(r_{AB,p})$$ | (4) |
식 (4)의 화학종 A와 화학종 B의 경로를 고려한 RAB값을 기반으로 연구자가 정의한 경계 값과 비교하여 제거 가능성을 결정한다. 이와 같이, Fig. 1과 같은 임의의 반응 시스템에서 DRGEP 방법을 적용할 경우 식 (5)~(8)과 같이 표현 가능하다.
| $$r_{AD,1}=r_{AB}\;\cdot\;r_{BD}$$ | (5) |
| $$r_{AD,2}=r_{AC}\;\cdot\;r_{CD}$$ | (6) |
| $$r_{AD,3}=r_{AC}\;\cdot\;r_{CE}\;\cdot\;r_{ED}$$ | (7) |
| $$R_{AD}^{DRGEP}=\max(r_{AD,1},r_{AD,2}\;,r_{AD,3})$$ | (8) |
2.2. 바이오디젤 화학반응 메커니즘
본 연구에 적용된 바이오디젤 기초화학반응 메커니즘은 선행 연구[14]에서 LLNL(Lawrence National Laboratory)의 Herbinet 등[1]이 제시한 바이오디젤 상세화학반응 메커니즘을 바탕으로 생성된 기초화학반응 메커니즘이다. 이 메커니즘은 바이오디젤 모사를 위해 Methyl decanoate, Methyl-9-decenoate, n-heptane 화학종을 포함하고 있으며, 1,107개의 화학종과 4,796개의 반응식으로 구성되어있다. 본 연구에서는 선행 연구[14]와 같이 바이오디젤을 모사하기 위한 구성 연료의 화학종 조성 비율 1:1:2를 사용하여 바이오디젤을 모사하였다. 또한, NOX 및 Soot 관련 화학종을 포함하기 위해 ERC(Engine Research Center)의 Wang 등[17]이 제시한 n-heptane 축소 메커니즘을 기초화학반응 메커니즘과 합성하였다.
본 연구에서 메커니즘 자동 축소화를 위해 ANSYS reaction workbench를 사용하였으며, DRGEP 방법과 연동하여, 생성된 기초화학반응 메커니즘의 오차율 비교를 위해 CHEMKIN-PRO를 사용하였다[18].
2.3. 메커니즘 자동 축소화
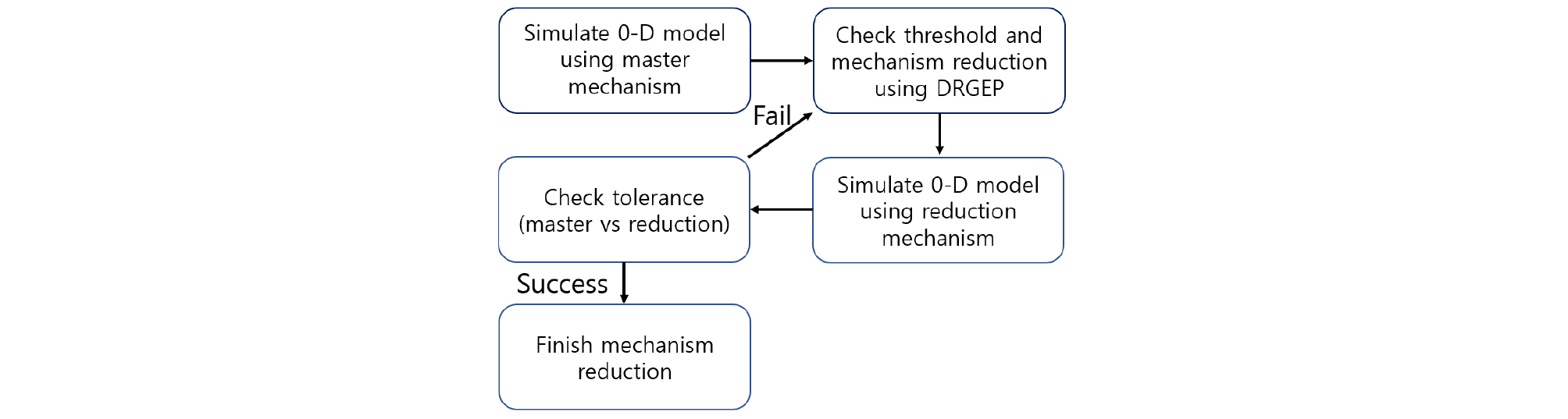
본 연구에서 메커니즘 축소를 위해 사용된 자동 축소화 과정을 Fig. 2를 통해 나타냈다. 먼저, DRGEP 방법을 적용한 메커니즘 축소를 위해 Table 1과 같이 압축착화연소 조건과 유사한 분위기 조건을 적용하여, 분위기 조건 변화에 따른 기상 상태의 연료와 산화제가 완전히 혼합된 균일 혼합과 연소 반응으로 압축착화연소 과정을 모사할 수 있는 0-D 정적 연소 해석 모델을 적용하여 메커니즘 축소를 위한 데이터를 생성했다.
Table 1. Operating conditions to reduce mechanisms
| Operating conditions | Range considered |
| Equivalence ratio | 0.5, 1.0, 1.5 |
| Residence time (ms) | 50 |
| Initial ambient temperature (K) | 700, 1100, 1500, 1900 |
| Initial ambient pressure (MPa) | 0.1, 2.0, 4.0 |
이후 생성된 연소 해석 결과를 고려하여 DRGEP 방법을 적용하였으며, 이 과정에서 설정된 표적 화학종 및 경계 값을 통한 메커니즘 축소 연구를 수행했다. 다음으로, 축소된 메커니즘을 적용하여 앞서 사용된 연소 모델 및 동일한 분위기 조건에서 연소 해석을 수행하였다. 이렇게 생성된 해석 결과를 DRGEP 방법이 적용되기 이전의 해석 결과와 비교하여 축소된 메커니즘의 오차율을 계산하였다. 이 과정에서 사용되는 오차율 계산법은 식 (9)와 같이 정의하였으며, 이를 메커니즘 오차율(T)로 명명하였다.
| $$T=\frac{\left|v_{master}-v_{skeletal}\right|}{(RT\times\left|v_{master}\right|+AT)}\times100(\%)$$ | (9) |
메커니즘 오차율에서 나타내는 vmaster는 DRGEP 방법을 적용하기 이전의 값을 의미하며, vskeletal는 DRGEP 방법이 적용된 메커니즘에 대한 값을 의미한다. 또한, RT는 상대 오차(Relative tolerance) 그리고 AT는 절대 오차(Absolute tolerance)이며, 메커니즘 오차율을 보정하는 역할을 수행한다. RT값은 증가할수록 메커니즘 오차율을 감소시켜 메커니즘의 축소를 더욱 증진시키고, AT값은 설정된 AT값보다 낮은 검증 인자 값에서 발생되는 오차를 제거하여 메커니즘 축소 효율을 증진시키는 역할을 한다. 이와 같이 계산된 메커니즘 오차율을 통해 오차율이 100% 이상인 경우 경계 값을 낮추며, 그렇지 않은 경우 경계 값을 높인다. 이를 통해 재설정된 경계 값을 적용하고, 앞서 설명한 축소 방법을 반복하여, 메커니즘 오차율 100% 이내를 만족하는 최대 축소된 최종 기초화학반응 메커니즘을 선정하였다.
2.4. 메커니즘 축소 환경 및 표적 화학종
본 연구의 목적인 표적 화학종 변화에 따른 영향을 확인하기 위하여, RT와 AT값 변화에 따른 메커니즘 축소율 및 점화지연 오차 확인을 통해 적절한 RT와 AT값을 선정했다. 이를 위해 DRGEP 방법은 총 2회 적용되고, RT값은 70~100(%)와 AT값은 1.0E-8, 1.0E-11을 사용했다. 또한, RT값 80(%)의 경우 AT값을 0, 1.0E-8, 1.0E-11으로 변경하며 AT값이 적용되지 않은 경우도 고려하였다. 이 과정에서 고려된 표적 화학종은 Table 3에 나타난 Case 1과 같이 적용하였다. RT와 AT값이 결정된 이후, 바이오디젤 메커니즘 축소와 관련된 선행 연구[15], [16]를 참고하여 Table 2와 같이 4가지 Case의 표적 화학종들을 적용하고, 그에 따른 결과를 비교 분석하였다. 기본적으로 연료, 산화제(O2, N2), 배출물(CO, CO2, NO), H2O 화학종이 메커니즘 내에 제거되지 않도록 표적 화학종으로 설정하였으며, 각 Case 별로 Table 2에서 나타난 Soot 생성과 관련된 화학종을 추가하였다.
Table 2. Cases of target species considering various species
| Case number | Target species |
| Case 1 | A4 |
| Case 2 | A1, A2, A3, A4* |
| Case 3 | HCO, H2O2, HO2 |
| Case 4 | H2O2, HO2, OH, C2H2, C2H4 |
Table 3. Operating conditions to evaluate the reduced mechanisms
Case 1과 Case 2에서 고려된 표적 화학종은 Soot 생성과 직접적인 관계를 가진 PAH(Poly Aromatic Hydrocarbon) 화학종으로, 특히 A4는 n-heptane 메커니즘 내에서 Soot 생성 개시종으로 사용되고 있다. 그리고 Case 3과 Case 4에서 고려된 화학종은 각각 Poon 등의 연구와 Cheng 등의 연구에서 사용된 표적 화학종을 적용하였다[15], [16]. 또한, 본 연구에서는 다양한 메커니즘 축소 결과를 객관적으로 평가하기 위해 메커니즘 축소율과 점화지연 오차율을 고려한 평가식을 식 (10)과 같이 정의하였고, 이를 통해 메커니즘 축소 결과를 비교하였다.
| $$Evalue=(R_{species}+R_{reactions})\times0.75-E_{ignition}\times0.25$$ | (10) |
여기서, Rspecies와 Rreactions은 합성된 메커니즘을 기준으로 화학종 및 반응식 개수에 대한 축소율을 나타내고, Eignition은 상세화학반응 메커니즘과 축소된 메커니즘 사이의 최대 점화지연 오차율을 나타낸다. 또한, 본 연구에서는 3차원 CFD 해석 연구에 축소 메커니즘을 적용하기 위해 메커니즘 축소율이 매우 중요하며 메커니즘 축소로 인한 해석 오차는 불가피한 것으로 판단하여 식 (10)의 메커니즘 축소율과 점화지연 오차율 사이의 계수를 각각 3:1 (0.75:0.25)로 구성하였다.
이와 같이 생성된 기초화학반응 메커니즘을 자세히 비교하기 위해 Table 1의 분위기 조건보다 자세한 Table 3의 조건을 적용하여 정적 연소 해석을 수행하였다. 또한, 해석 결과를 사용하여 바이오디젤 상세화학반응 메커니즘과 축소된 메커니즘의 점화지연 비교 및 오차율 계산을 수행했다. 이 과정에서 계산된 오차율은 식 (9)의 오차율 계산법이 아닌 식 (11)의 일반적인 오차율 계산법을 사용하였으며, 각 분위기 조건에서 최대 오차율 값을 식 (10)의 Rignition 값으로 사용하였다.
| $$E_{ignition}=\frac{v_{master}-v_{skeletal}}{v_{master}}\times100(\%)$$ | (11) |
3. 결과 및 고찰
3.1. 메커니즘 합성
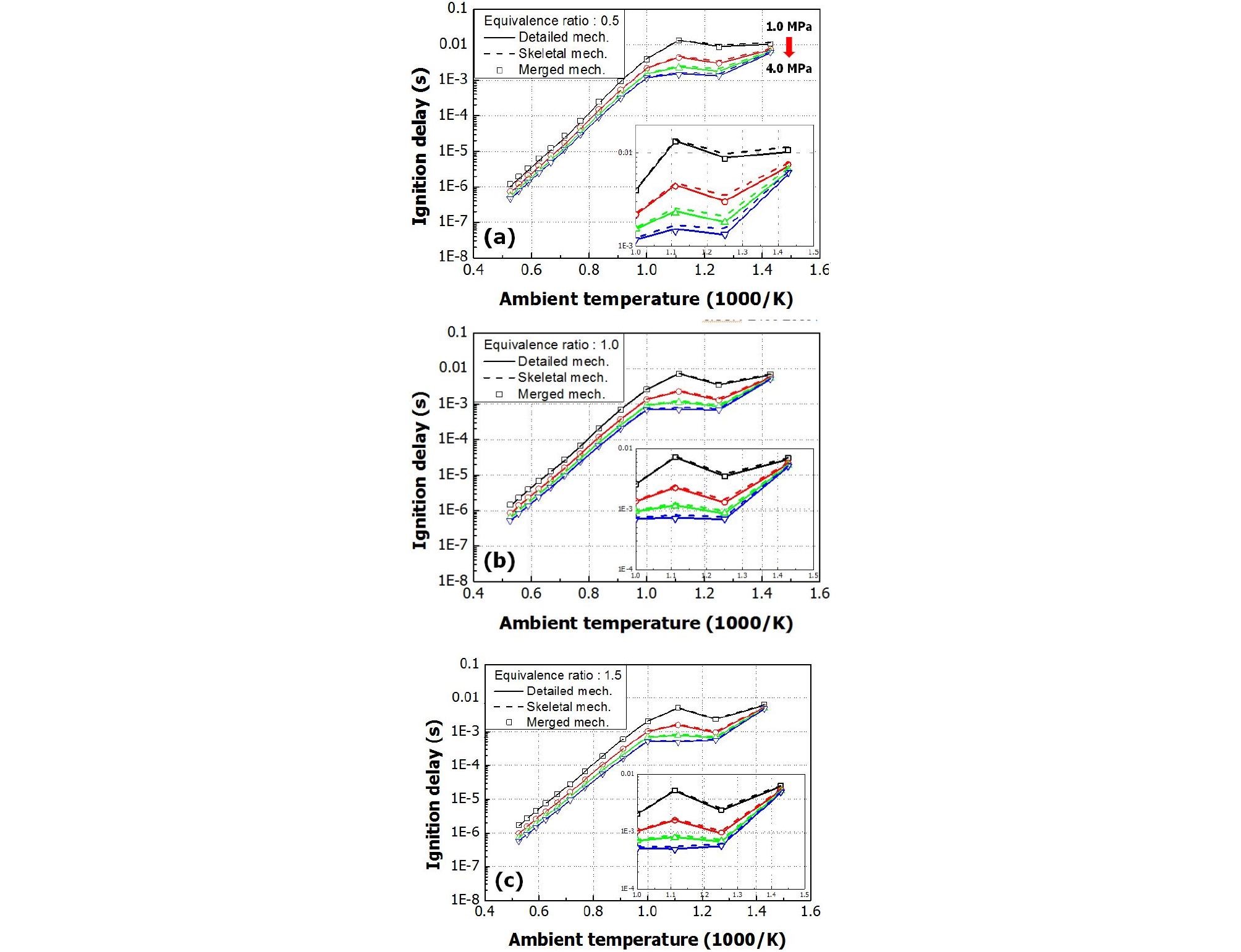
Fig. 3은 세 종류의 메커니즘인 바이오디젤 상세화학반응 메커니즘, 선행 연구[14]를 통해 생성된 기초화학반응 메커니즘 그리고 기초화학반응 메커니즘과 n-heptane 메커니즘을 합성한 합성 메커니즘의 정적 연소 해석에 대한 점화지연 결과를 비교한 그래프이다. 선행 연구[14]에서 생성된 기초화학반응 메커니즘과 상세화학반응 메커니즘의 최대 오차는 NTC(Negative Temperature Coefficient) 영역에서 약 16%로 나타났으며, 고온의 분위기 온도 조건에서는 상세화학반응 메커니즘 결과와 거의 일치했다. 본 연구에서 기초화학반응 메커니즘과 n-heptane 메커니즘의 합성 결과, 화학종과 반응식의 개수가 각각 1,144개와 5,057개로 증가하였다. 또한, NTC 영역에서의 점화지연 최대 오차는 약 5%까지 감소하였으며, 낮은 당량비 및 고온의 분위기 온도 조건에서는 점화지연 오차가 증가하여 오차율이 약 16%로 나타났다. 이러한 결과는 n-heptane 메커니즘 내에 포함된 저온 연소와 관련된 화학종이 기초화학반응 메커니즘과 합성되어 나타난 결과로 사료된다.
3.2. 메커니즘 축소 환경 설정
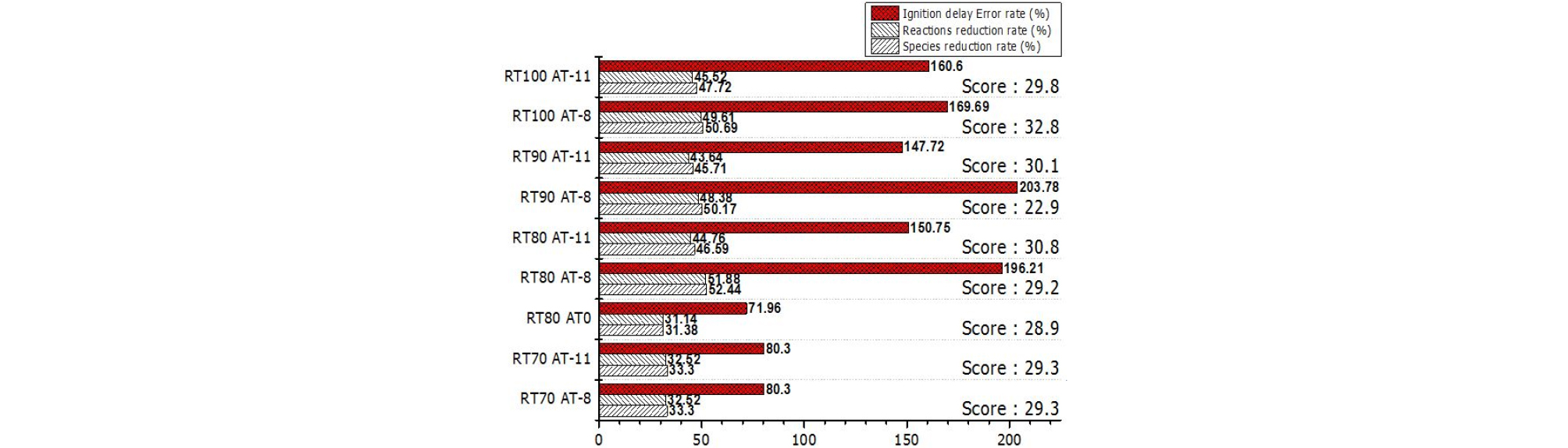
Fig. 4는 RT와 AT값 변화에 따른 메커니즘 축소 결과를 나타낸 그래프이다. 각 Case의 명명법은 적용된 RT값과 AT값의 지수로 사용하였다. 먼저, RT80의 경우를 통해 AT값이 적용될 때 메커니즘 축소율이 높아지는 것을 확인할 수 있다. 이는 AT값이 적용되지 않을 경우, 매우 작은 값에서 발생하는 오차까지 고려하여 메커니즘 축소가 제한되어 나타나는 현상이며, AT-8과 AT-11을 비교할 경우, 2.3절에서 언급된 AT값의 역할로 인해 AT-8의 메커니즘 축소율이 높은 것을 확인할 수 있다. 하지만, RT70의 경우 AT-8과 AT-11의 차이가 없는 것을 확인할 수 있다. RT값 변화에 따른 영향은 전체적으로 RT값이 증가할수록 축소율이 증가하지만, 선행 연구[14]에서 확인했듯이 축소 조건에 따라 적용되는 경계 값이 다르기 때문에 RT80 AT-8과 같은 경우, 높은 RT값이 적용된 조건보다 메커니즘 축소율이 높아진다.
축소율과 점화지연 오차율 간의 관계를 비교 시, 메커니즘 축소율이 40% 이상 증가하면 점화지연 오차율이 급격하게 증가한다. 또한, RT80 AT-8과 RT100 AT-8에서 확인할 수 있듯이, 서로 유사한 메커니즘 축소율을 보이지만, 점화지연 오차율이 서로 상이하게 나타났다. 따라서, 이러한 결과를 통해 메커니즘 축소 환경이 미치는 영향을 분석 가능하며, 메커니즘 축소 과정의 경계 값과 관련된 축소 환경을 파악하는 것이 중요한 요소임을 확인할 수 있다.
식 (10)을 통해 축소 메커니즘의 평가 점수를 비교할 경우, RT100 AT-8이 메커니즘 축소율 대비 낮은 점화지연 오차율을 갖는 것으로 나타났다. 이러한 결과를 통해 RT100 AT-8이 가장 적합한 것으로 판단되지만, 다른 표적 화학종을 고려함으로서 A4 화학종만을 고려한 RT100 AT-8보다 효율적인 메커니즘 축소 가능성을 비교하기 위해 RT100 AT-8 메커니즘 다음으로 점수가 높은 RT80 AT-11 메커니즘을 기준으로 표적 화학종 변화에 따른 영향을 확인하였다.
3.3. 표적 화학종 변화에 따른 영향
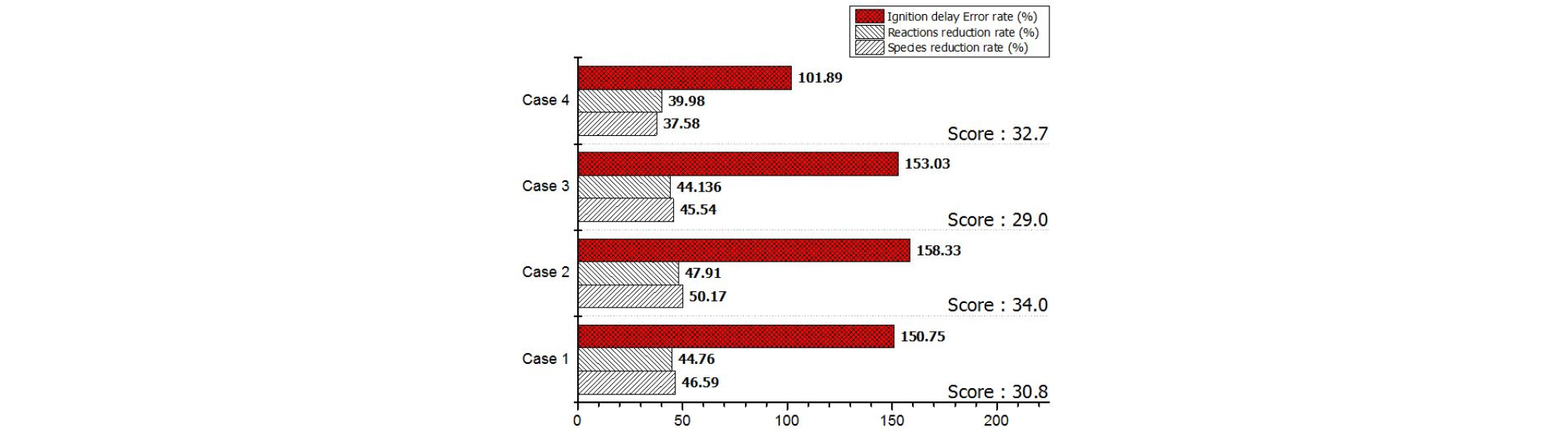
Fig. 5는 표적 화학종 변화에 따른 메커니즘 축소 결과에 대해 나타낸 표이다. 분석 결과, Case 2가 가장 높은 점수로 나타났으며, Case 4, Case 1, Case 3 결과 순으로 높은 점수를 보였다. 특히, Case 2는 3.2절에서 RT100 AT-8보다 높은 점수를 보인다. Case 1 및 Case 2와 같이 배출물 화학종을 표적 화학종으로 설정할 경우, 다른 Case들과 비교하여 상대적으로 메커니즘 축소율이 높은 것을 확인할 수 있다. 반면, Case 4와 같이 많은 수의 중간 화학종을 표적 화학종으로 고려할 경우, 메커니즘 축소율이 적어지는 것을 확인할 수 있지만, 점화지연 오차율은 다른 Case 대비 낮은 오차율을 보인다.
이와 같은 결과를 통해 표적 화학종의 종류에 따라 메커니즘 축소율 및 점화지연 오차율이 개선될 수 있으며, DRGEP 방법을 적용한 메커니즘 축소 시 표적 화학종의 결정이 매우 중요한 인자임을 알 수 있다. 또한, 메커니즘 축소 목적에 따라 두 가지 방향의 화학종 설정이 가능한 것을 알 수 있다. 첫 번째로 메커니즘의 크기를 축소하고자 하는 경우, 최종 생성 화학종으로 고려하는 것이 좋으며, 두 번째로는 메커니즘 축소에 따른 오차율을 감소하고자 하는 경우와 중간 화학종을 고려하는 것이 효율적인 것으로 사료된다. 하지만, Case 3과 같이 중간 화학종을 설정하면 낮은 축소율과 높은 점화지연 오차율이 발생할 수 있는 가능성이 있으므로 최종 연소 생성물인 배출물과 관련된 화학종을 표적 화학종으로 설정하는 것이 적절한 것으로 판단된다.
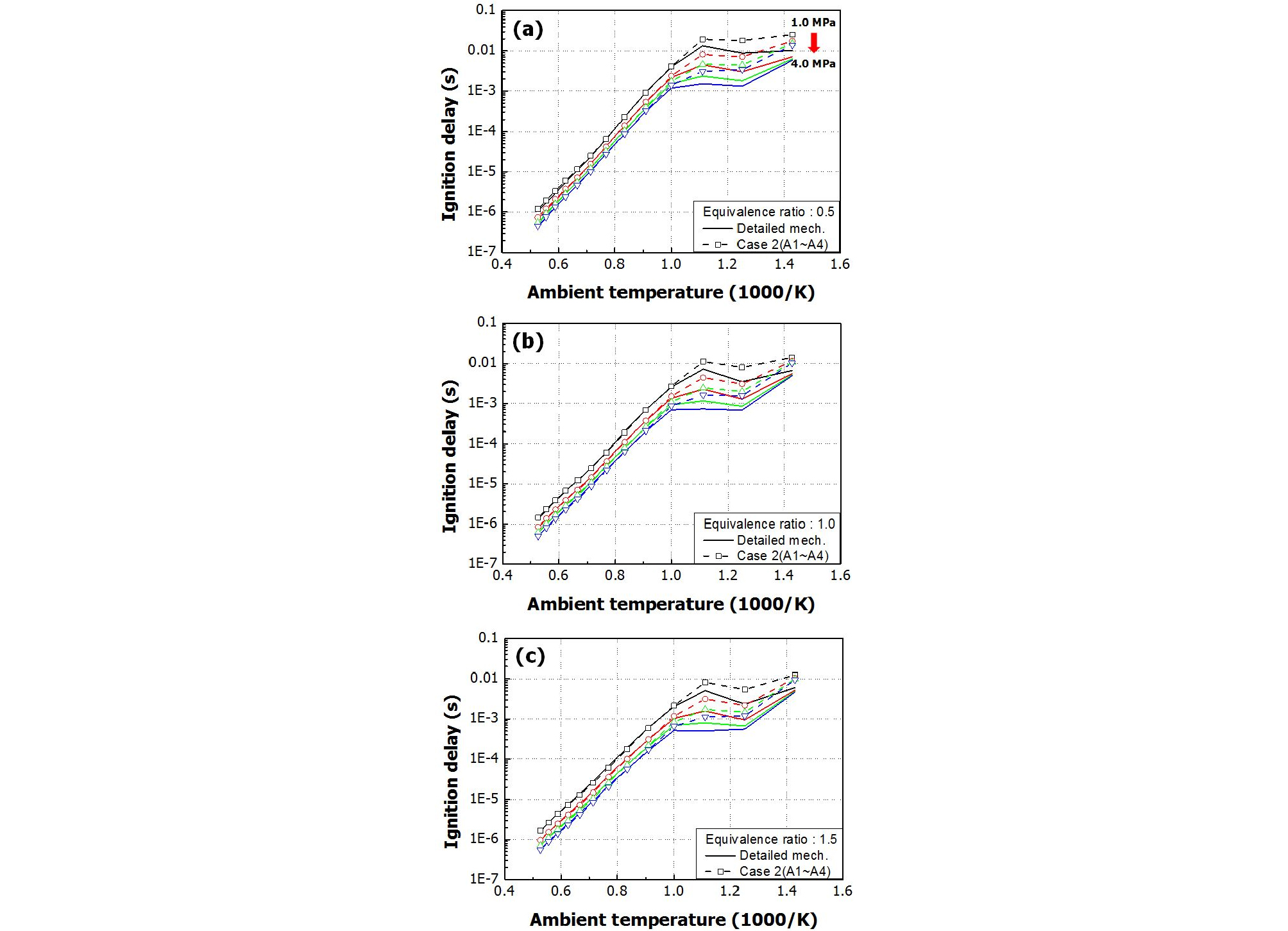
이와 같은 결과를 통해, 표적 화학종 변화에 따른 메커니즘 축소 결과가 가장 우수한 Case 2의 점화지연 결과를 Fig. 6에 나타내었다. 선행 연구[14]와 마찬가지로 DRGEP 방법 적용 시 NTC 영역에서의 오차가 증가하는 것을 확인할 수 있으며, 특히, 분위기 온도 800K, 분위기 압력 4MPa 그리고 당량비 0.5 조건에서 가장 높은 오차율을 보였다. 이와 같은 점화지연 오차는 Case 2를 포함한 모든 Case에서 발생하였으며, 이를 통해 표적 화학종의 변경으로 인한 NTC 영역에서의 점화지연 오차율 감소 효과는 미흡한 것으로 판단된다.
4. 결 론
본 연구는 DRGEP 방법이 적용된 메커니즘 축소 과정의 표적 화학종 변화가 메커니즘 축소화에 미치는 영향을 수치 해석적으로 비교 분석하여 다음과 같은 결론을 얻었다.
1)기초화학반응 메커니즘과 n-heptane 메커니즘을 합성한 결과, 1,144개의 화학종과 5,051개의 반응식으로 구성된 메커니즘을 생성하였으며, 합성을 통해 NTC 영역의 점화지연 오차가 감소된 것을 확인하였다.
2)다양한 RT와 AT값을 고려한 메커니즘 축소 결과, RT값과 AT값 증가에 따른 메커니즘 축소율은 증가하는 경향을 보이지만, 각 Case들 마다 점화지연 오차율 결과는 서로 다른 경향을 보였다. 이를 통해 메커니즘 축소 환경 설정에 따른 메커니즘 축소 효율 증진이 가능할 것으로 사료된다.
3)다양한 표적 화학종 변화에 따른 메커니즘 축소 결과, 최종 연소 생성물이 고려된 Case 2(A1, A2, A3, A4)가 가장 높은 평가 점수를 보였다. 따라서, DRGEP 방법을 적용한 메커니즘 축소 시 표적 화학종의 선정은 매우 중요한 요소임을 확인하였다.
4)메커니즘 축소를 위한 표적 화학종 선정 시, 중간 화학종보다 최종 연소 생성물과 관련된 화학종을 표적 화학종으로 고려하는 것이 적합한 것으로 판단된다.
기호설명
A : Species A
AT : Absolute tolerance
ε : User specified threshold value
I : i-th reaction
T : Error tolerance of mechanism
RT : Relative tolerance
RA :Production rate of species A
rAB :Normalized contribution of B to the production rate of species A
vA : Stoichiometric coefficient for the species A
w : Rate of progress variable