1. 서 론
2. 신형 GP3 RTE의 개요
3. 수치해석 방법
3.1. 계산 영역 모델
3.2. 지배방정식 및 경계조건
3.3. 연소 모델링
4. 해석 결과 및 토론
4.1. 흡기과정(1st: -20°~240°)
4.2. 압축-팽창 과정(1st: 240°~360°~540°)
4.3. 배기 과정(1st: 540°~+80°)
4.4. 흡기과정(1st: -20°~240°)
4.5. 압축-팽창 과정(1st: 240°~360°~540°)
4.6. 팽창말기-배기과정(1st: 420°~720°~80°)
5. 결 론
1. 서 론
현재 보편적으로 가장 많이 사용되는 원동기는 4행정 RE(reciprocating engine)이다. 이 엔진은 피스톤의 왕복운동을 회전 운동으로 변환하는 크랭크 기구, 흡 ․ 배기 밸브 제어장치 등 엔진 구조가 비교적 복잡하며, 균일한 회전력을 얻기 위해서는 다기통이 요구된다[1]. 현재 소형 시스템의 원동기로도 RE가 비교적 많이 사용되고는 있으나, RE는 소형화되면 효율은 떨어지고[2], 특히 열·발전 설비를 겸비해야 하는 mini-CHP에서는, 진동 및 소음도 개선이 필요하다고 지적되고 있다[3].
RTE(rotary engine)는 크랭크 기구 없이 실린더 압력 변화를 직접 회전 운동으로 변환시키며, 흡 ․ 배기 시스템도 단순하여 엔진의 부품 수가 RE보다 훨씬 적어져 소량 생산에도 유리하다. 대표적인 RTE로는 1960년대 초에 개발된 WE(Wankel engine)을 들 수 있다[4]. 이 WE을 기준으로 RTE의 장 ․ 단점을 간략히 요약하면 다음과 같다[5], [6]. 장점으로는 구조가 단순하며, 마찰 손실이 적고, 엔진 중량 대비 출력이 높으며, 고속회전에 유리하며, 진동 및 토크 변동이 작다. 단점으로는 연비, 공해 성능이 나쁘며, 씰링(sealing) 및 윤활 시스템이 복잡하며 내구성이 떨어진다고 지적되어 있다. 이들 단점들은 WE의 로터 및 하우징의 구조에서 기인한다고 할 수 있다. 즉, 연소실을 회전하는 로터에 설치해야 하며, 그 형상도 얇은 사각형이며, 화염 전파 방향으로 이동하는 공간에서 연소가 진행되어야 한다. 그리고 누설 막음용 씰(seal)들도 회전하는 내부 로터 면에 위치시켜야하기 때문에 윤활에도 어려움이 따른다.
10여 년 전부터 LiquidPiston사는 새로운 형식의 로타리 엔진(X엔진)[7]을 제안하여 개발 중에 있으며 그 형상은 WE과는 많이 다르다. 즉, WE은 하우징의 로브(lobe) 수가 2인 반면에, X 엔진은 로터의 로브수가 2이며 하우징은 로브수가 3이다. 두 엔진은 기본적으로 GP(Gerotor pump)의 형상 함수[8], [9]를 이용하여 설계된다. LiquidPiston사에 의하면 X엔진은 WE의 장점들은 계승하면서 다음과 같이 단점들은 개선한 것이라고 주장한다. 즉, WE에서는 회전하는 로터의 3면에 사이드(side), 꼭짓점(apex) 및 코너(corner) 씰(seal) 3 종류가 필요하다. 반면, X 엔진에서는 이들 씰링 기구를 단순화하여 가스 누출 문제를 개선하려고 한 것이다[10]. 또 X 엔진에서는 구조상 연소실을 고정된 하우징에 설치할 수 있으며, 연소실 형상도 비교적 자유롭게 할 수 있다. 그리고 흡 ․ 배기 포트의 위치 선정에 의해 쉽게 과팽창 행정도 구현할 수도 있다고 한다[11]. 개발 초기에는 수랭식 70 HP급 디젤 엔진을 대상으로 엔진의 구동 및 기본 원리를 검증하였다[12]. 그 후 70 cc급 공랭식 가솔린 엔진을 대상으로 연구를 수행하여 소형 카트에 적용한 바 있다[13]. 최근에도 발전기, 소형 항공기, 전기차용 비상 엔진(range-extender)등을 목표로 내구성능, 열전달 성능, 씰링 성능을 개선하기 위한 연구가 지속되고 있다[14], [15], [16].
본 연구진도 앞에서 언급한 X 엔진이 mini-CHP용 엔진으로 적합할 것으로 판단하고 수요 업체와 함께 수년 전부터 연구에 착수하게 되었다[17]. 본 연구는 3D CFD 해석을 통해 실험용 엔진(1차)을 대상으로 흡 ․ 배기, 연소실 관련 설계 인자들의 타당성을 검토하는 것이다. 이전[18] 논문에서는 모터링 운전 조건을 대상으로 해석법의 타당성과 비연소 조건의 유동특성을 고찰하였다. 본 논문에서는 이전 논문을 계승하여 연소조건을 대상으로 CFD 해석법의 타당성을 검증하고, 연소유동 특성을 고찰하여 앞에 언급한 본 엔진의 중요 성능 인자들의 설계 타당성을 검증하기 위한 자료를 도출하기 위한 것이다.
2. 신형 GP3 RTE의 개요
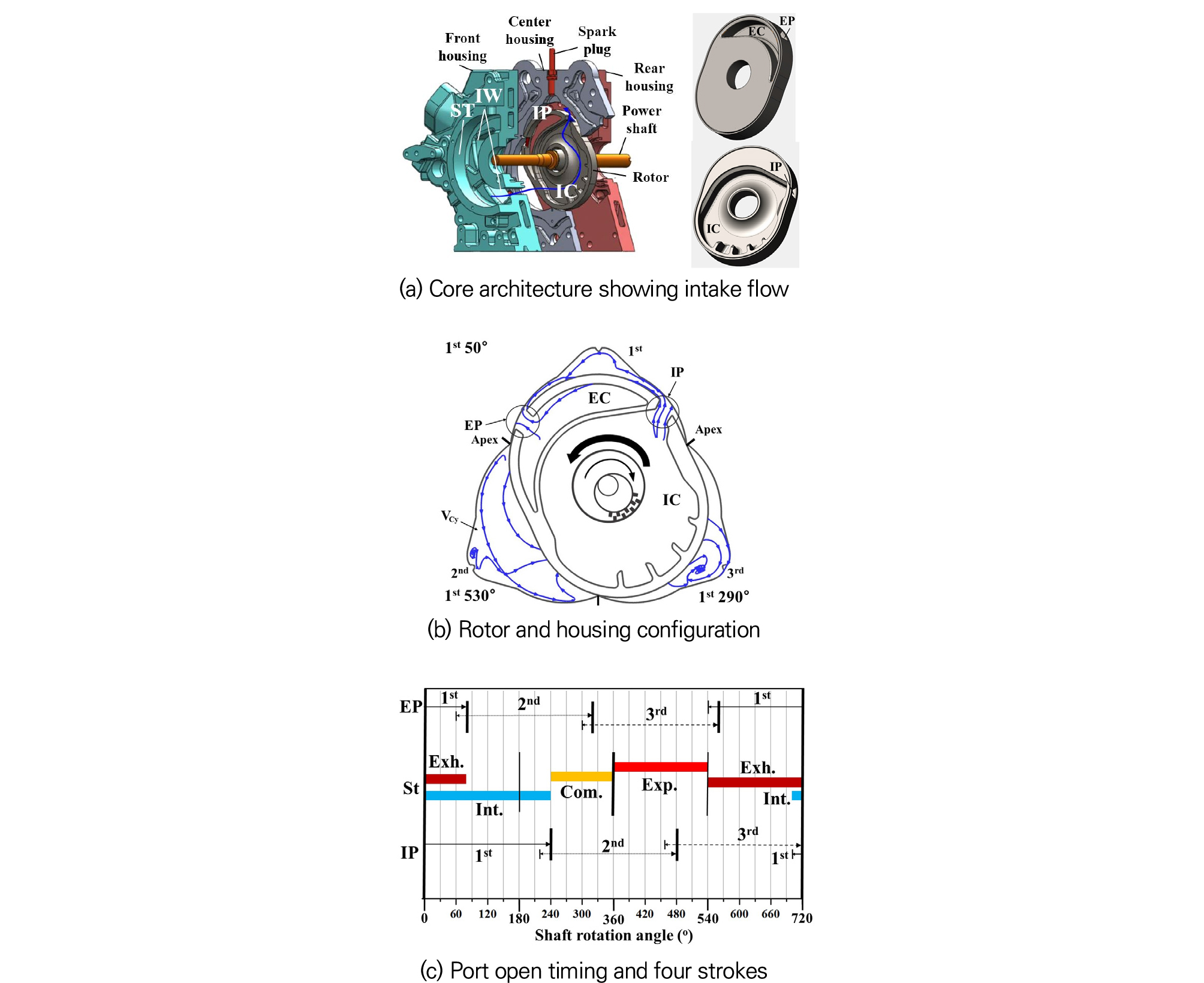
Fig. 1은 본 연구팀이 개발 중인 GP3(Gerotor pump type with three lobes) RTE(rotary engine)의 구조 및 행정 과정을 간략히 나타낸 것으로, 이전 논문[18]에서 비교적 자세히 제시한 바 있다. 용량은 336 cc인 소형이며, Fig 1(a)에 해당하는 코어 부분의 크기는 폭 150 mm, 직경 300 mm 정도이다.
Fig. 1(a)는 핵심 부품의 내부 구조를 흡기 방향에서 제시한 것이다. 중앙에 편심 동력축(power shaft)과 이에 연동하는 타원형 로터가 회전 부품에 해당한다. 로터 양면에는 그림과 같이 IC(intake chamber), EC(exhaust chamber)가 설치되어 있으며, 그 외주 면에는 각각 IP, EP가 가공되어 있다. 하우징은 로터를 3면에서 감싸는 형태로 배치되며, 로터의 폭이 실린더 폭에 해당한다.
Fig. 1(b)는 본 엔진의 작동과정을 간략히 묘사하는 로터-하우징 단면도이다. 로터 형상은 로브 수 2인 에피트로코이드 함수로 결정되며, 하우징 형상은 편심 회전하는 로터의 최외각 궤적에 의해 결정된다[8], [9]. 하우징 내부는 3개의 로브(lobe)로 균등 분할되어 있다. 로브 상단에는 간극 체적(VC)이 가공되어 있고, 하우징-로터사이의 캐비티(cavity)가 실린더 체적(VCy)에 해당한다. 이 체적은 로터가 1회전 하면 2회 증감을 반복한다. IP, EP의 위치를 적절히 조절하면, 첫 번째 체적 증감은 흡입-압축 행정, 두 번째 증감은 팽창-배기 행정으로 사용하여 4행정을 구현한다. 본 엔진은 동력축이 시계방향으로 2회전 하면 로터는 반시계 방향으로 1회전 하도록 설계되어 있다[8]. 본 논문에서는 동력축 회전각도(SRA)를 상부의 1st Cy가 TDC인 상태를 기준(0°)으로 정의하였다. 그림은 SRA = 50°인 경우로 1st Cy는 흡입초기, 왼쪽의 2nd는 팽창 말기(1st의 530°), 오른쪽의 3rd는 압축 말기(1st의 290°)를 나타내고 있다.
Fig. 1(c)는 SRA에 따른 IP/EP 오픈 구간, 1st Cy의 행정(stroke) 구간을 나타낸 것이다. 참고로, IP/EP 오픈 각도는 이들이 각 로브의 양 꼭짓점을 완전히 통과하는 각도로, 로터 회전각(240°)에 포트 폭( = 20°)을 합한 값이 된다. 1st Cy를 기준으로 IP는 해당 사이클 시작 전 –20°(700°)에서 오픈하여 VCy 최대인 180°를 지나 240°에서 닫히도록 설계되어 있다. EP는 540°에서 오픈하여 다음 사이클의 80°에서 닫힌다. 그리고 IP/EP 오버랩 구간은 –20°~80°이다. 본 엔진에는 IP/EP가 이웃하는 실린더에 동시에 오픈되는 중첩구간이 존재한다. 예로, IP 220°~240°, EP 60°~ 80°이 이에 해당하다. 또 포트 출구-하우징의 틈새 높이가 낮은 경우에는 흡 ․ 배기 유량은 포트 면적(A)보다 (포트 너비) × (틈새 높이)로 정의되는 유효 면적(EA)에 의해 결정된다(Fig. 1b). IP/EP 오버랩 구간에는 이들 면적(A, EA) 간에는 많은 차이가 있다. 이들 두 특성은 본 엔진에 고유한 것으로 이들 인자가 성능에 미치는 영향에 대해 각별히 주의할 필요가 있다.
3. 수치해석 방법
3.1. 계산 영역 모델
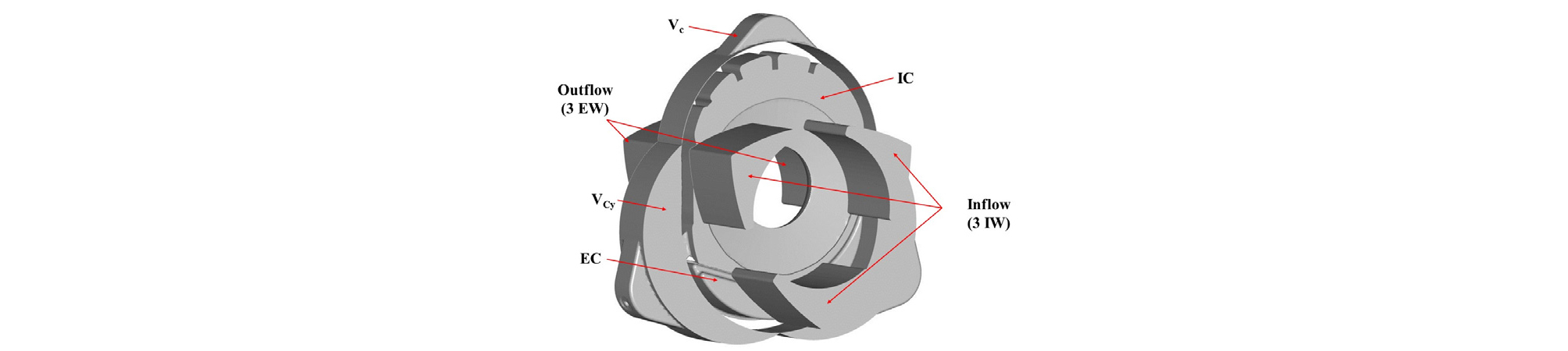
Fig. 2는 계산 영역 모델을 나타낸 것으로, Fig. 1의 IW~EW 사이에 해당하며, 곡선인 EW 유로도 IW 유로와 같이 직선 유로로 단순하게 하였다. 실제 실험용 엔진에서 흡기 방향의 흡기관, 쓰로틀 및 ST(surge tank), 또 배기 방향의 배기관은 생략한 것이다. 그림에서 음영 부분의 작동 유체 유동 공간에 해당하며, 중심의 하얀 공간은 동력축에 해당하며, 중간의 하얀 부분은 로터의 고체 몸체에 해당한다. 따라서 CFD 해석은 CH4/air 혼합기가 3개의 IW를 통해 IC로 유입된 후에 IP를 통해 Cy로 유입되어 압축, 연소, 팽창 과정을 거치고, 배기가스는 EP를 거쳐 EC로 배출된 후에 EW를 통해 외부로 배출되는 과정을 모사하는 것이다.
3.2. 지배방정식 및 경계조건
본 해석은 상용 CONVERGE 프로그램을 이용하였다. 해석에 필요한 수식은 매뉴얼[19]에 상세히 기술되어 있으며, 비연소 유동에 대해서는 이전 논문[18]에서 간략히 정리되어 있다. 여기에는 이전에 기술되지 않은 화학종 보존식 및 연소 모델에 대해 간략히 정리하겠다.
3.3. 연소 모델링
3.3.1. 화학종 보존식
화학종 보존 방정식은 다음과 같다.
| $$\frac{\partial(\rho Y_m)}{\partial t}+\frac{\partial(\rho u_jY_m)}{\partial x_i}=\frac\partial{\partial x_i}\left(\rho D\frac{\partial Y_m}{\partial x_i}\right)+S_m$$ | (1) |
여기서, 은 화학종의 질량 분율, 는 질량 확산 계수, 은 생성항이다. 난류 질량 확산계수는 계수는 다음과 같이 주어진다.
| $$D_t=\frac{\nu_t}{S_{c_t}}$$ | (2) |
여기서 는 turbulent Schmidt number이다. 위 화학종 방정식의 생성항은 다음의 SAGE 연소 모델에서 구해진다.
3.3.2. SAGE 연소모델
본 해석에서는 SAGE 연소모델[20]을 사용하였다. 이 모델은 잘 알려진 CHEMKIN[21] 형식의 반응 해석 과정을 기반으로 한다. 단, 본 모델은 난류-반응 간의 간섭 현상은 무시하고 있으나, 복잡한 엔진 연소 과정에서 반응속도에 의존성이 높은 노킹, 오염물질 등을 합리적으로 예측한다고 알려져 있다[22]. SAGE는 CFD solver가 수송방정식을 풀기 직전에, 다음과 같이 각 셀에서의 반응 과정을 등적 혹은 등압 연소로 가정하여 풀고 새로운 화학종 농도를 구하고, 수송방정식을 푼다.
Turns[23]에 의해 기술된 바와 같이 다단계 반응식은 다음과 같이 기술된다.
| $$\sum_{m=1}^Mv'_{m,r}\chi_m\Leftrightarrow\sum_{m=1}^Mv''_{m,r}\chi_m\;\;\;\;\mathrm{for}\;r=1,2,\;...R$$ | (3) |
여기서 과 는 반응물과 생성물에 대한 반응양론계수이며, M은 화학종 수, R은 전체 반응식 수이다.
화학종 m의 생성속도는 다음과 같다.
| $$\dot{w_m}=\sum_{r=1}^Rv_{m,r}q_r\;\;\;\;\;\;\mathrm{for}\;m=1,2,\;...\;M$$ | (4) |
여기서,
| $$v_{m,r}=v''_{m,r}-v'_{m,r}$$ | (5) |
| $$q_r=k_{fr}\prod_{m=1}^M\lbrack X_m\rbrack^{v'_{m,r}}-k_{rr}\prod_{m=1}^M\lbrack X_m\rbrack^{v''_{m,r}}$$ | (6) |
순방향 반응 속도상수는 다음의 Arrhenius 식을 사용하고, 역방향의 속도상수 는 평형상수를 이용하여 계산한다.
| $$k_{fr}=A_rT^{b_r}e^{(-E_r/R_uT)}$$ | (7) |
위에 기술한 식들을 이용하면, 각 셀에 대한 질량 및 정적 연소로 가정한 에너지 보존식은 다음과 같다.
| $$\frac{d\lbrack X_m\rbrack}{dt}={\dot w}_m\sum_{}^{}$$ | (8) |
| $$\frac{dT}{dt}=\frac{V\frac{dP}{dt}-\sum_m(h_m{\dot w}_m)}{\sum_m(\lbrack X_m\rbrack{\overline c}_{p,m})}$$ | (9) |
위 방정식들은 각 계산 단계(time-step)마다 계산되며, 화학종은 바로 새로운 값으로 제공되나, 온도는 위 반응속도상수를 구하는 데에만 사용된다.
3.3.3. 반응기구 및 그 축소법
본 연구에서 연료는 도시가스를 사용하였으며, 상세 반응기구로는 GRI-Mech 3.0[24]을 이용하였다. 본 계산에서는 AZ(adaptive zoning), DMR(dynamic mechanism reduction)을 함께 사용하여 계산 시간을 단축하였다. AZ[25]는 우선, 열역학 상태량을 기준으로 유사한 셀들을 동일 존(zone)으로 분류한다. 다음에 각 존의 평균 물성치를 이용하여 새로운 화학종의 질량분율을 SAGE로 한꺼번에 계산한다. 그리고 이 결과를 각 셀과 존의 차이를 고려하여 보정한 질량분율들을 각 존의 모든 셀에게 할당(mapping)하는 방식이다. DMR은 타겟 화학종들에 대한 상대 공헌도들을 합산하여, 각 셀에서 공헌도가 낮다고 여겨지는 화학종 및 반응식을 상세 반응식으로부터 삭제하는 축소법이다. 이 축소법으로는 DRGEPSA[26]을 사용하고 있으며, 그 상세 방식에 대해서는 여기서는 지면 관계상 생략한다. AZ 및 DMR을 결합하여 사용하면 각 존(bin)마다 고유의 축소 반응 기구를 갖게 된다.
4. 해석 결과 및 토론
본 해석법의 타당성은 우선, 모터링 조건에서 검토하여 3 mm-AMR 방식을 채택하면 그리드 크기에 의존하지 않는 결과를 얻을 수 있었다[18]. 여기서는 비정상 연소장의 수렴성, 연소 모델에 대한 검증에 한정한다.
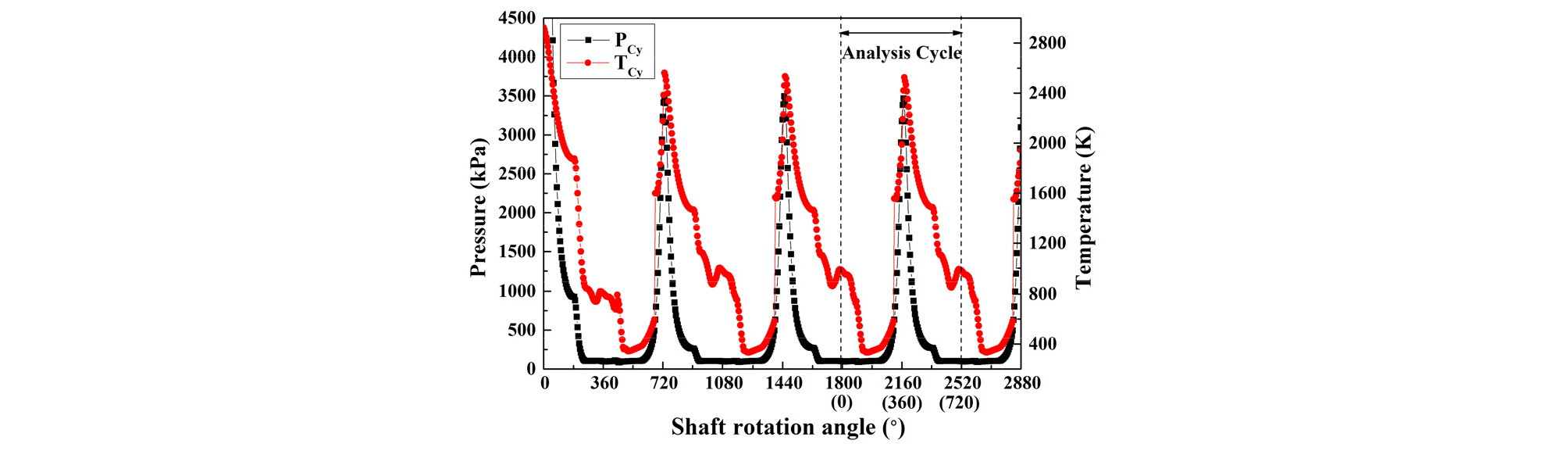
Fig. 3은 1st Cy를 기준으로 특정 위치(Vc의 5지점)의 평균 압력, 온도 변화를 도시한 것이다. 계산 시작점은 1st Cy 기준으로 점화시점( bTDC -50°) 조금 전부터 시작하였으며, 첫 번째 피크치는 초기 가정 치에 의존하기 때문에 무의미하며, 전 사이클 대비 피크치들의 평균 감소율은 3번째는 0.78%, 4번째는 0.23% 정도이며, 3~4번째는 사이클에서는 분포도 거의 동일하다. 이를 근거로 계산 구간은 2,880°까지 수행하였으며, 해석 대상 사이클은 1st Cy 기준 1,800°~2,520°로 하였다.
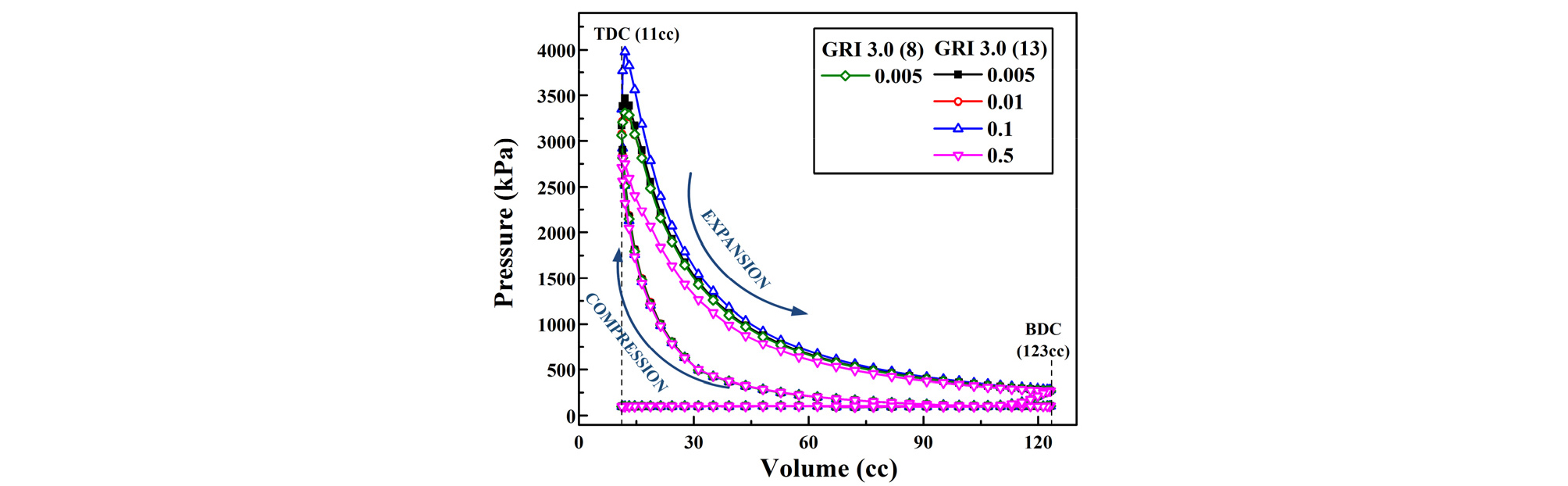
Fig. 4는 상세 반응기구의 축소법에 따른 P-V 선도를 비교한 것이다. 축소 반응은 TS(target species)들에 대한 상대 공헌도들을 합산하여 임의 ET(error tolerance) 이하인 화학종 및 반응식을 삭제하는 방식으로 구해진다. 본 해석에서는 TS는 8종 13종 두 경우를, ET는 0.005~0.5까지 변화시켰다. 해석 결과를 보면, TS 변화에 대해서는 결과에 거의 차이가 없으며, 계산 시간도 큰 차이가 없어 TS는 13종을 사용하였다. 반면, ET는 계산 결과에 다소 민감하며, 합리적인 해를 얻으려면 0.1 이상을 사용해야 할 것으로 판단된다. ET 0.1~0.005 범위에서 계산 시간은 TS 13종 및 ET 0.005를 기준(20시간, 16 ch. multi-PC)으로 약 5% 정도로 그리 크지 않았다.
위 P-V 선도를 바탕으로 본 엔진의 성능을 판단해 보면 도시 마력은 3.3~3.9 kW, 도시 효율은 21~24% 정도가 됨을 알 수 있다. 이 효율은 상용 소형 왕복동 엔진(1기통 120 cc)[2]의 제동효율 23%와 비교해 큰 차이가 없음을 알 수 있다.
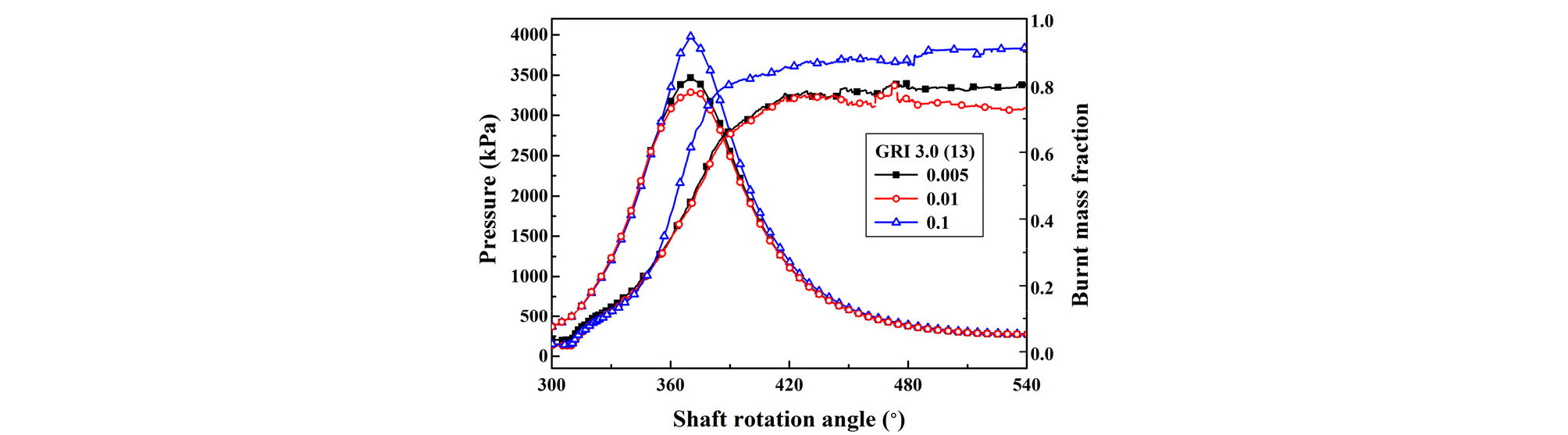
Fig. 5는 반응 축소법에 따른 압력 및 질량 연소율[1]을 나타낸 것이다. 축소법에 따라 연소율은 0.8~0.9까지 변하며, 이에 따라 얻어지는 도시 마력, 효율 등에 상당한 영향을 미치고 있음을 알 수 있다. 단, 현 단계에서는 판단 자료 부족으로 최적인 축소법에 대한 논의는 추후로 미루고자 한다. 또 본 논문은 연소 유동 특성을 파악하여 설계 인자들의 적합성을 검토하기 위한 것이다. 따라서 본 논문에서는 반응 축소법으로 TS 13종, ET 0.005를 자의적으로 선정하였다. 이 경우는 최종 연소율이 0.8 정도로 미연가스가 상당량 발생하며, 본 엔진의 약점으로 예상되는 소염 현상을 명확히 관찰하는 측면에서 유리할 것으로 판단하였다.
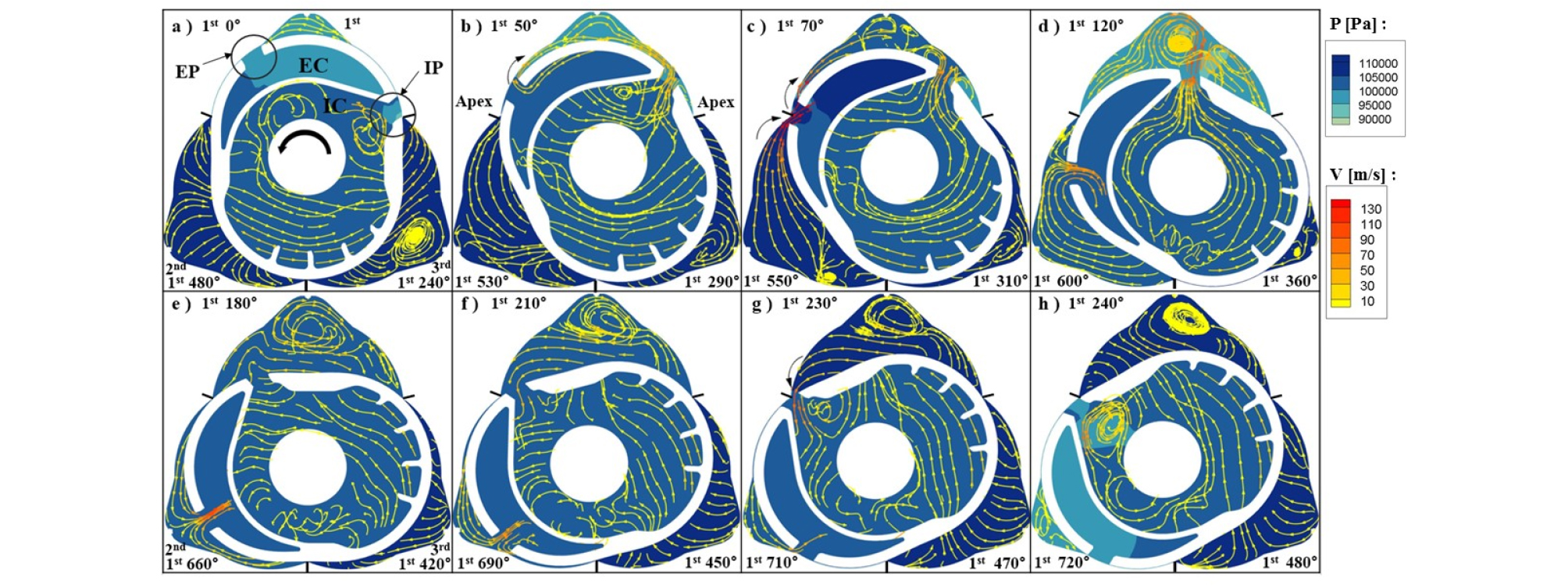
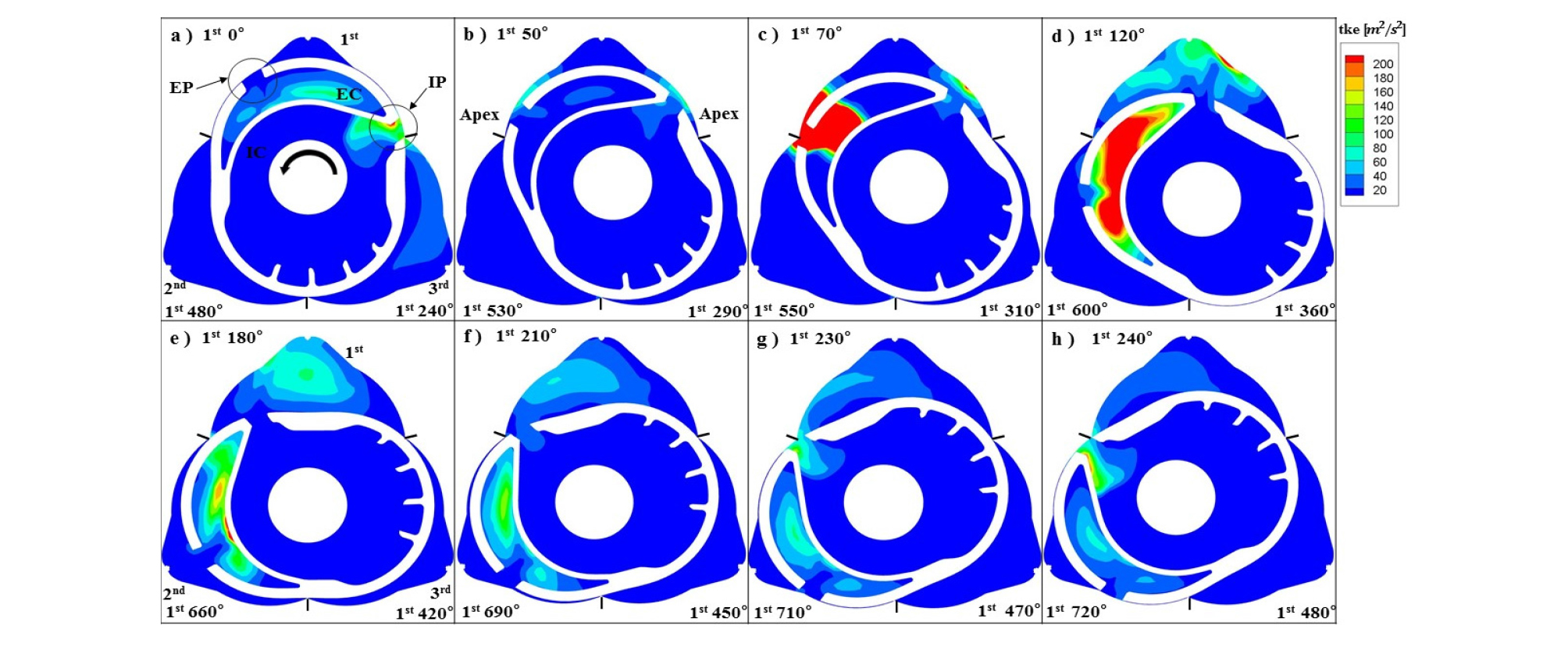
Fig. 6~7은 SRA에 따른 유선, 난류 운동 에너지(TKE)의 변화를 나타낸 것이다. 그림은 1st Cy를 기준으로 흡기과정(0°~240°)만을 제시한 것이나, Cy간 위상차를 고려하면, 3rd는 1st의 압축-팽창과정(240°~480°), 2nd는 1st의 배기과정(480°~720°)과 일치한다. 따라서 본 그림에서는 사이클 전 과정을 관찰할 수 있으며, 각 실린더 옆에 표기된 1st의 각도가 행정 각도를 의미한다. 그림에서1st 70° (Fig. c), 230°(Fig. g)는 각각 EP, IP가 이웃 Cy에 중첩하는 경우이다.
Fig. 6에서 바탕색은 IC, EC의 압력을 나타내며 짙은 색이 높은 압력이다. 유선은 빨간색이 고속이며, 3차원 유동을 2차원으로 제시하다 보니, 중첩하거나 벽면을 관통하는 것처럼 보이기도 한다. Fig. 7에서는 빨간색이 TKE가 높은 경우이다. 이들 결과를 바탕으로 행정별 유동 특성을 정리하면 다음과 같다.
4.1. 흡기과정(1st: -20°~240°)
초기는 IP/EP 오버랩 구간으로, IC 신기가 IP를 통해 고속으로 유입되면서 난류도 강해지며(1st 50°), EC 배기도 EP를 통해 재유입(EGR) 됨(1st 70°)을 알 수 있다. 중반에는 시계 및 반시계 방향의 와류가 공존하며 이들 거동에 의해 연소실 중앙부에서 난류강도가 높아짐을 알 수 있다. 말기에는 IC로 역 배출되는 유동에 의해 다음 실린더로 유입될 신기의 난류 강도도 강해짐을 알 수 있다.
4.2. 압축-팽창 과정(1st: 240°~360°~540°)
압축은 1st 240°~360° 구간에서 일어나며 유동은 Cy 중앙으로 이동하고, 팽창은 1st 360°~540° 구간으로 로터면 방향으로 이동하면서 시계 방향의 와류를 형성된다. 이 압축-팽창 과정에서의 난류강도 변화는 크지 않다.
4.3. 배기 과정(1st: 540°~+80°)
배기 초기에는 배출 유속이 100 m/s 이상으로 매우 커서 EP 주변은 물론 이웃 실린더의 EGR 영역까지 난류 강도를 증가시킨다(1st 550°). 또 초 ․ 중반에 분출되는 배기에 의해 EC 벽면에는 강한 충돌 분류가 형성되면서 EC의 난류 강도도 증가한다. 후반인 1st 720°에서는 배기 과정은 끝나고, 이후 80°까지는 EP-IP 오버랩 구간으로 EC의 가스가 역흡입(EGR)되고 있다.
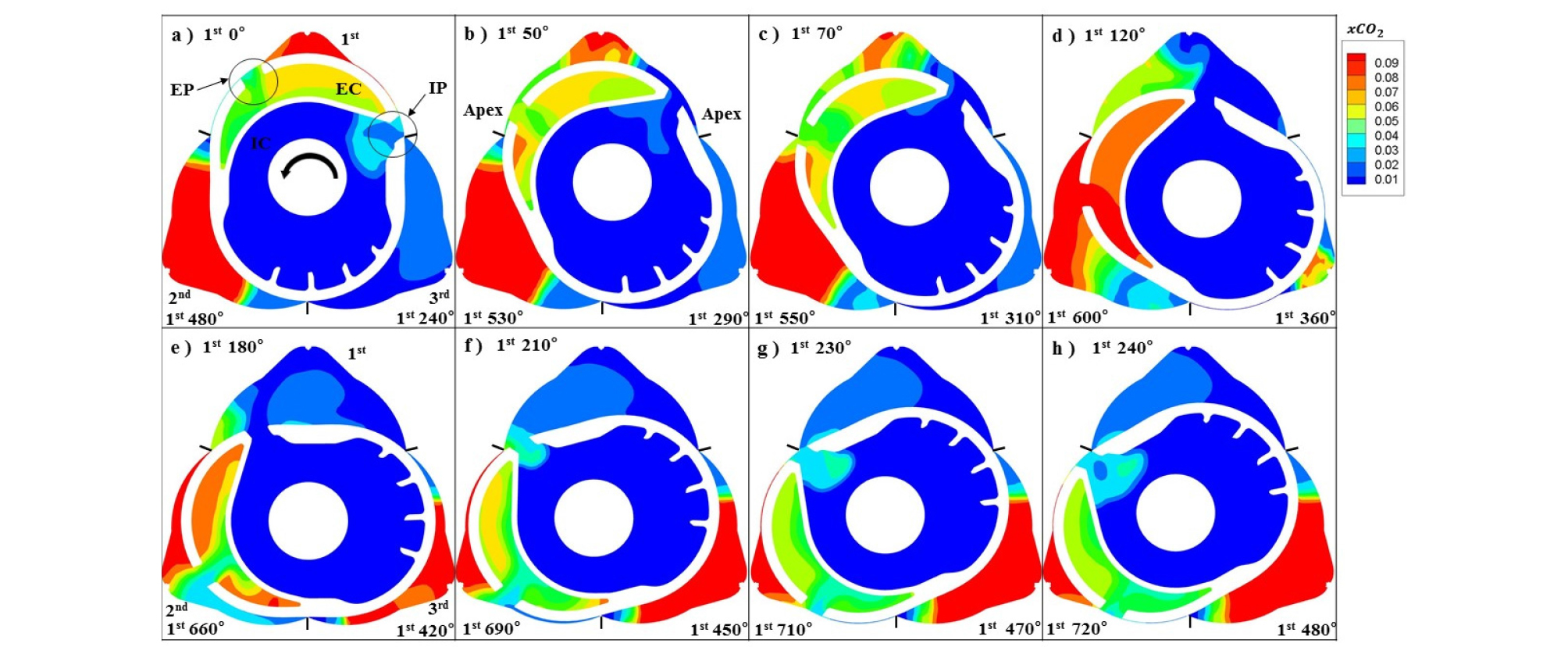
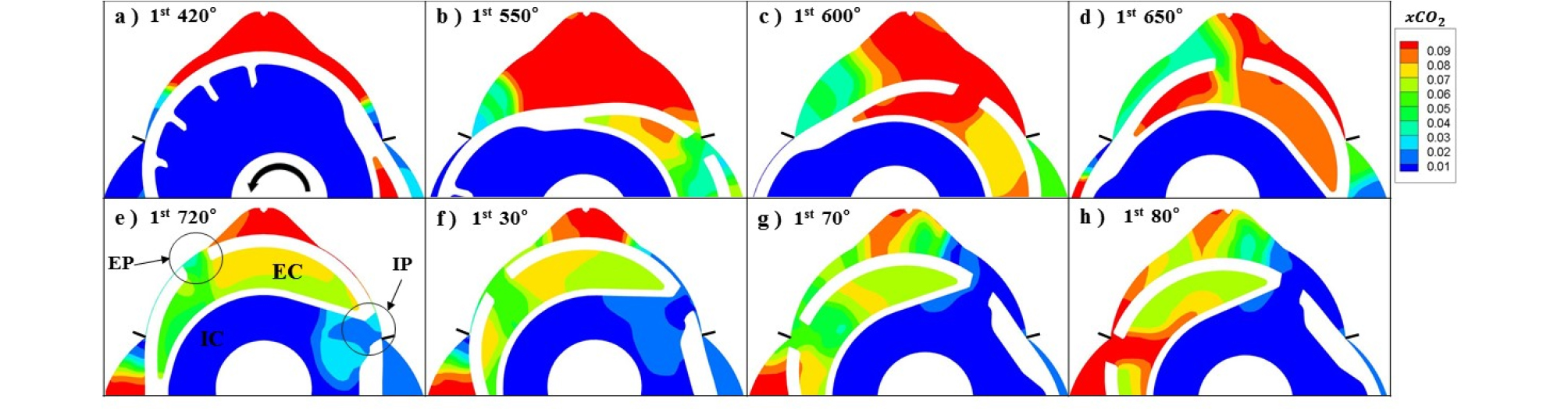
Fig. 8은 앞 그림과 동일한 방법으로 SRA에 따른 CO2 몰분율의 변화를 도시한 것으로, 전 사이클에서의 연소 특성을 관찰할 수 있다. 공기비 1인 CH4의 배기 중 이론 CO2 농도 9.5%를 참고로 하면, 그림의 빨간색(9% 이상)은 거의 완전 연소된 배기가스이며, 파란색(1% 이하)은 신기이며, 녹색(4%)은 미연 가스를 포함하는 배기가스를 나타낸다. 이 결과를 이용하여 행정별 연소 특성을 고찰하면 다음과 같다.
4.4. 흡기과정(1st: -20°~240°)
초기(1st 0°) VC에는완전 연소에 가까운 배기가스(빨간색)로 충만 되어 있다. 흡기가 진행되면서 IP로는 새로운 혼합기(파란색), EP로는 미연성분을 포함한 배기가스(파란색)가 재흡입(EGR)되고 있다. 후반으로 진행되면서 CO2를 포함하는 EGR 영역이 실린더의 좌측에 형성된다. 실질적인 압축이 시작되는 240° 시점에서 CO2 농도에서 구한 EGR율[27] 약 16%가 된다.
4.5. 압축-팽창 과정(1st: 240°~360°~540°)
본 운전 조건은 점화시기가 bTDC 50°(SRA = 310°)이며, TDC(360°)에서는 연소가 본격적으로 진행되고 있으며, 420°에서는 연소실 말단까지 화염이 전파되나, 연소실 양 끝단의 좁은 틈새 영역에서 화염전파가 일어나지 않는 소염존이 형성되고 있음을 알 수 있다. 이 소염 영역 본 엔진의 고유한 특성이나 효율을 개선하기 해결해야하는 과제이다. 이에 대해서는 추후에 연구를 수행하고자 한다.
4.6. 팽창말기-배기과정(1st: 420°~720°~80°)
Fig. 9는 팽창말기에서 오버랩 구간을 포함한 배기 과정에서 EGR 거동 및 중첩하는 EP의 영향을 명확히 관찰하기 위해, 1st Cy를 기준으로 CO2 몰분율 변화를 제시한 것이다. 본 그림을 해석함에 있어서는 Fig. 1(c)에 제시한 포트 오픈 타이밍도 참고하였다.
팽창 말기(420°)에는 연소실 양 끝단에 소염 영역이 존재하며, 배기 초기(550°)는 EP 중첩기간(3rd~1st, 540°~560°)으로 1st의 오른쪽 소염 미연 성분이 배출되면서 그 일부는 다음(3rd) 실린더로 재흡입(EGR)되고 있다. 이후 거의 연소된 배기가스(빨간색)가 배출되다가, 다시 650°~720° 구간에서 왼쪽 소염 미연성분이 배출되고 있음을 알 수 있다. 720° 이후에는 오버랩 구간으로 배기는 없고, EP를 통해 배기가스를 재흡입(EGR)한다. 그리고 배기말기의 EP 중첩기간(1st~2nd, 60°~80°)에는 앞 실린더(2nd)의 오른쪽 소염 영역의 가스가 배출되면서 그 일부가 1st Cy로 재흡입(EGR)되고 있음을 알 수 있다. 따라서 본 엔진에서 EGR은 SRA = 720° 지난 오버랩 기간에 이루어지며, 그 초 ․ 중반에는 자신의 배출한 가스를 재흡입하나, 그 후반인 EP 중첩 구간에는 앞 실린더에서 배출한 가스의 일부가 재흡입된다. 이들 각각이 EGR 총량에 미치는 영향에 대해서는 추후 검토하겠다.
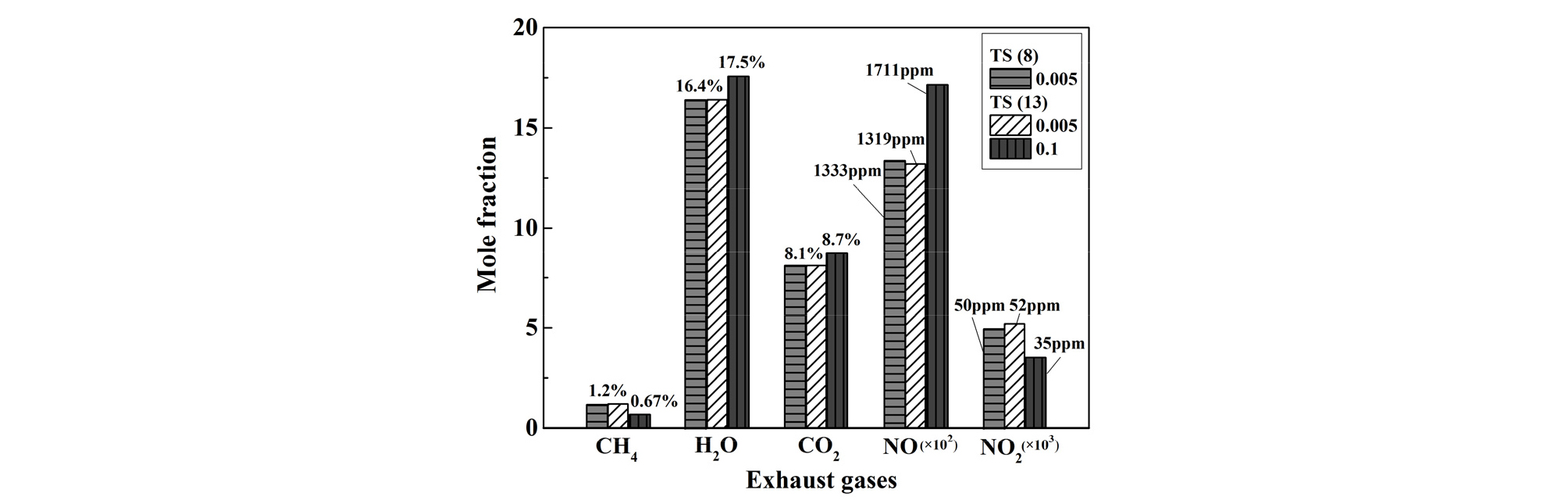
Fig. 10은 앞에서 언급한 반응기구 축소법 중에서 TS(target species) 13종, ET(error tolerance) 0.005를 중심으로, TS를 8종으로 ET를 0.1로 변화시킨 경우의 배기특성을 비교한 것이다. 참고로, ET 0.005인 경우 TS에 따른 P-V 선도(Fig. 4), 질량 연소율도 거의 동일함을 확인하였고, 본 그림에서 배기 특성에도 큰 차이가 없음을 알 수 있다. 다음에 TS가 13인 경우 ET에 따른 차이를 살펴보면, ET가 0.1의 경우가 최고 압력도 다소 높아지며(Fig. 4), 질량 연소율(Fig. 5)도 다소 높아짐을 확인하였다. 본 그림을 보면 이들 차이가 배기 특성에도 잘 나타나고 있음을 알 수 있다. 즉, ET가 0.005에서 0.1로 변하면 미연 성분은 감소하면서 NO2는 다소 감소하나 NO가 크게 증가하여 NOx 농도는 증가함을 알 수 있다. 이와 같은 ET에 따른 배기특성의 변화에 대해서는 추후에 상세히 검토하고자 한다. 위 결과를 보면 ET가 0.005~0.1 범위에서는 NO 및 NO2 배출 농도는 대체적으로 1,500 ppm, 50 ppm 정도로 NOx 배출 특성도 합리적으로 예측하고 있다고 판단된다. 따라서 본 해석법은 엔진의 주요 설계 변수에 따른 엔진의 출력 및 배기 성능을 검증하는데 유용하게 사용할 수 있을 것으로 판단된다.
5. 결 론
본 연구는 실험용 엔진(1차)을 대상으로 3D CFD 해석을 통해 흡 ․ 배기, 연소실 관련 설계 인자들의 타당성을 검토하는 것이다. 본 논문에서는 이전의 모터링 조건의 유동 해석결과를 계승하여 연소 조건을 대상으로 해석법의 타당성을 검증하고, 연소유동 특성을 고찰하여 주요 설계 인자들의 타당성을 검증하는 것이다. 얻어진 결과는 다음과 같다.
1) 본 해석에서는 4번째 사이클에서 수렴된 결과가 얻어지며, GRI-Mech 3.0 상세 반응의 축소법으로 TS (target species) 8~13종, ET(error tolerance) 0.005%~ 0.1% 범위에서 합리적인 결과가 얻어지며, 계산시간의 차이는 약 5%정도이다.
2) 위 연소 모델에 의한 최종 질량 연소율은 0.8 ~0.9 정도로, 연소실 양 끝단의 틈새 영역에 구조적인 소염 영역이 존재하며, 효율을 개선하기 위해서 해결해야 할 과제임을 알았다.
3) 본 실험용 GP3 RTE(용량 336 cc, 유효 압축비 8.5)의 예상 성능은 도시 마력 4 kW, 도시 효율 24%(3,000 RPM 조건)정도로 동급의 상용 소형 왕복동 엔진과 유사함을 알았다.
4) 본 엔진에서 EGR은 SRA = 0° 이후의 오버랩 기간에 이루어지며, 초반에는 배출한 가스를 재 흡입하나, 후반에는 이웃 실린더가 배출한 가스를 흡입한다.
5) 본 해석법은 NOx를 포함한 배기가스 성분을 합리적으로 예측하여, 주요 설계 인자를 검증하는데 유용하게 사용할 수 있다. NOx 배출 농도는 본 조건에서 약 1,800 ppm 정도이다.
기호설명
Alphabet
A : area
AZ : adaptive zoning
AMR : adaptive mesh refinement
BDC : bottom dead center
bTDC : before top dead center
C : clearance
Cy : cylinder
EA : effective area
EC : exhaust chamber
EP : exhaust port
ET : error tolerance
EW : exhaust window
IC : intake chamber
IP : intake port
IW : intake window
P : pressure
RE : reciprocating engine
RTE : rotary engine
SRA : shaft rotation angle
ST : surge tank
TDC : top dead center
TS : target species
V : volume
WE : wankel engine