1. 서 론

온도와 농도의 정량 측정은 연소 현상 분석에 있어 매우 중요하다. 가장 일반적인 측정 방법들로 열전대, 가스 크로마토그래피, 전기화학적 측정 방법들이 있다. 그러나, 이러한 방법들은 프로브의 삽입이 요구되어 측정하고자 하는 대상 근처의 유동과 반응을 교란할 뿐 아니라, 열전대를 통한 외부와의 열 교환 그리고 가스 크로마토그래피 프로브 내에서의 반응으로 인해 오차를 야기한다. 열전대의 경우, 고온 환경 측정 시 복사 열전달에 의해 실제보다 낮은 온도를 도출한다. 이와 같이 측정에 영향을 미치는 요소들을 피하기 위해 비접촉식 온도 및 농도 측정 기법들이 활발히 연구되고 있다.

비접촉식 측정 기법은 크게 음향학적 기법과 광학적 기법으로 분류된다. 음향학적 기법[1], [2], [3]은 주로 온도 측정을 위해 활용되어왔으며, 음파의 전달 속도가 매질의 온도의 함수로 주어진다는 사실에 기반한다. 광학적 기법들에는 Rayleigh scattering[4], [5]과 Coherent anti-Stokes Raman spectroscopy(CARS)[6], [7], tunable diode laser absorption spectroscopy(TDLAS)[8], [9], [10], [11], [12], laser-induced breakdown spectroscopy(LIBS)[13], [14], [15], [16] 등이 있으며, 빛과 매질 간 산란, 흡수, 발광의 상호작용을 활용한다. Rayleigh scattering과 CARS는 주로 온도 측정에, LIBS는 국부 당량비의 측정에, TDLAS는 온도와 농도 측정에 사용되어 왔다.

TDLAS는 레이저 빛이 매질을 통과할 때 파장에 따라 흡수되는 정도인 흡광도를 측정하는 기법이다. 흡수선을 파장에 대해 적분한 흡광도는 측정대상의 몰분율, 선강도, 압력, 경로 길이의 곱으로 표현된다. 이 중, 선강도는 온도의 함수이다. 따라서, 온도나 농도 구배가 없을 시, 동일한 레이저 경로에 대해 획득한 하위 에너지 준위를 공유하지 않는 서로 다른 두 파장의 흡광도 비율은 온도만의 함수가 된다[9], [10]. 대개 두 흡수선의 하위 에너지 준위는 측정하고자 하는 온도 범위보다 각각 높고 낮도록 선정하여, 두 흡수선의 선강도 비율이 온도에 대해 꾸준히 증가하거나 감소하는 경향성을 갖도록 한다. 먼저 흡광도 비율로부터 온도를 획득하고, 이후 흡광도를 해당 온도에서의 선강도로 나누어줌으로써 측정 화학종의 몰분율을 구한다. 그러나, 선강도의 비율을 통해 온도를 측정하는 이중 파장 흡수 분광 온도 측정법은 HITRAN[17] 데이터베이스 내 선강도 오차(5 ~ 10%)로 인해 온도와 몰농도 두 결과 모두에 오차가 발생하는 구조적 문제를 가져, 파장 선정에 특별한 주의가 필요하다.

한편, 연소 연구 분야에서 LIBS는 레이저 펄스를 기체 매질 내 공간 상 한 지점에 집중시켜 플라즈마를 형성하고, 플라즈마로부터의 발광 분광을 통해 화학적 원소 조성을 측정하는 기법으로써 연구되어 왔다. 고온의 플라즈마로 인해 매질 내의 모든 분자들은 원자 또는 이온화된 원자로 분해된다. 이때, 발생하는 발광 스펙트럼은 다수의 원자 발광선들을 포함하는데, H, O의 발광 원자선들의 비율은 당량비에 선형적으로 비례한다[14], [15], [16].

본 연구에서는, LIBS와 TDLAS 복합을 통한 온도-농도장 재건 기법을 새로이 제시한다. 기법의 검증을 위해 반경방향으로 대칭인 온도 분포 및 농도 분포를 갖는 연소장을 대상으로 측정을 진행하였다. LIBS를 사용하여 먼저 반경방향으로 당량비를 측정하고, 연소가 완료되었다는 가정 하에 연소 후 가스 내 수증기의 몰분율을 예측하였다. 다음으로, 7185.6 cm^-1 파수 근방의 빛을 발산하는 파장 가변형 레이저 다이오드를 사용하여 버너 중심으로부터의 거리별 파장별 흡광도를 측정하고, inverse Abel transform을 통해 거리별 흡광도로부터 반경방향 흡수계수 분포를 재건하였다. 중심파수 7185.6 cm^-1의 선강도는 500 K 이상의 온도에서는 꾸준히 감소하므로, 측정하고자 하는 온도 범위에 대해 선강도는 온도와 1 대1 대응관계를 갖는다. LIBS로부터 측정된 몰 농도와 TDLAS로부터의 흡수 계수장을 통해 온도장을 최종 재건하였고, 열전대를 사용해 측정한 온도장과 비교, 분석하였다.

2. 이 론

TDLAS는 Beer-Lambert 방정식에 근거한다. Beer-Lambert 방정식은 레이저 입사 세기에 대한 측정 영역 투과 후 레이저 세기 비율의 자연로그로, 식 (1)로 주어진다.

$A_v$ 는 파장별 흡광도(spectral absorbance)이고, $I_0$ 는 레이저 입사 세기, $I$ 는 투과 세기이다. 파장별 흡광도는 파장별 흡수계수 $k_v$의 측정 길이 $L$ 에 대한 경로 적분으로 주어진다. 식에서 파장별 흡수계수는 에너지 준위 i와 j 사이의 천이에 대응하는 선강도($S_{ij}$), 측정 영역 내의 흡수 화학종 몰분율, 전체압력($P$), 그리고 파수(wavenumber)에 따른 선모양 함수(${\varphi }_v$)의 곱으로, 식 (2)로 주어진다.

선모양 함수는 식 (3)을 만족토록 한다.

따라서, 파장별 흡광도와 흡수계수의 관계식은 식 (4)와 같이 나타나며 흡수계수는 식 (5)로 주어진다.

여기서, 온도의 함수인 선강도 $S_{ij}$ 는 식 (6)로 계산된다.

$T_{ref}$는 기준온도인 296 K이며, $S_{ij}\left(T_0\right)$ 는 기준온도에서의 선강도, $Q\left(T_0\right)$ 는 기준온도에서의 분자 부분 함수(molecule’s partition function), $Q\left(T\right)$는 온도 $T$ 에서의 분자 부분 함수, $c_2$는 second radiation constant, 는 천이 중심 파수, ${}_{2}E``$는 해당 천이의 하위 에너지 준위(lower energy level)이다.

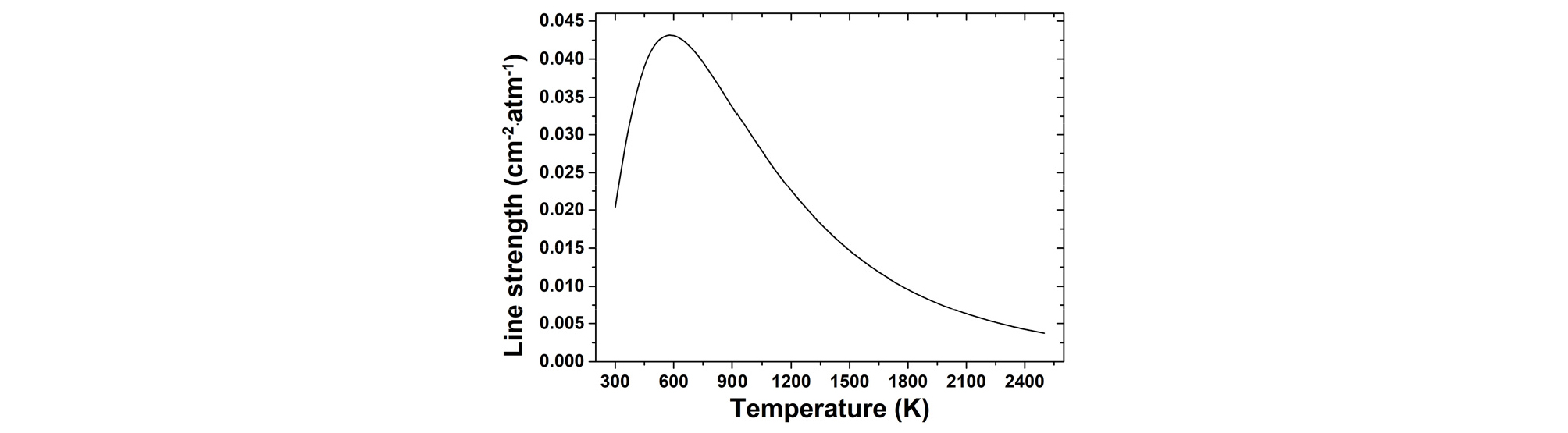
본 연구에서는 7185.6 cm^-1를 중심 파수로 갖는 흡수선들을 사용해 레이저 흡수 분광을 진행하였다. 해당 중심 파수의 흡수선은 단일 흡수선으로 보이나 실제로는 인접한 3개의 흡수선이 중첩되어 있다. Fig. 1은 7185.6 cm^-1 근처 흡수 선강도의 합을 온도에 따라 나타낸 결과로, 선강도는 온도가 증가함에 따라 약 500 K에서 최고값을 보인 후 감소한다.

Fig. 1.

Temperature dependence of the linestrength of water vapor at 7185.6 cm^-1.

3. 실험 방법

3.1. Flat Burner 및 열전대 실험 셋업

Fig. 2는 실험 셋업을 보여준다. 본 연구에서 반경방향으로 대칭의 연소장을 생성하는 McKenna 버너를 사용하였다. 버너는 평판 화염을 생성하는 원판형 금속 폼과 주변의 동축류를 제공하는 금속 폼으로 구성된다. 중심 축에는 노즐이 있으나 연구에서는 사용하지 않았다. 중심 금속 폼의 직경은 60 mm, 바깥 금속 폼의 외경은 70 mm, 그리고 중심 노즐의 직경은 12.5 mm이다. 공급되는 공기와 메탄의 유량은 mass flow controller들을 사용해 조절하였다. 연소 공기의 유량은 20 slpm으로 고정하였고, 메탄 유량을 조절하여 당량비를 0.73~1.01 범위로 변화시켰다. 동축류는 10 slpm 유량의 공기로 형성하였다. 결과 검증을 위해, type B 열전대를 motorized linear stage(LSQ series, Zaber)에 설치하여 화염의 반경방향 온도분포를 측정하였다. 열전대가 주변 유동과 열평형에 도달된 상태에서 온도 측정이 진행될 수 있도록, linear stage의 스캔 속도는 0.2 mm/s로 충분히 느리게 설정하였다.

Fig. 2.

Schematic of TDLAS and LIBS setups on flat flame burner.

3.2. TDLAS 실험 셋업

TDLAS는 7185.6 cm^-1를 중심파수로 갖는 파장 가변형 레이저 다이오드(EP1391-9-DM-B01-FM, Eblana Photonics)를 사용해 진행되었다. 레이저 다이오드로부터 발산되는 단파장 빛의 파수와 세기는 다이오드 온도를 고정할 시, 공급되는 전류에 대해 선형적으로 조절된다. 전류는 함수 발생기(GW INSTEK AFG-2225)에서 발생하는 신호에 따라 전류 조절기(Thorlabs LDC201CU)를 통해 다이오드로 공급되며, 다이오드 온도는 별도의 조절기(Thorlabs TED200C)에 의해 일정하게 유지된다. 함수 발생기는 10 Hz의 ramp 파형을 발생하였다. 레이저 빛은 광 섬유를 사용해 전달하였고 collimating lens(Thorlabs TC12APC- 1310)를 사용해 직선으로 조사하였다. 측정대상(매질)을 통과한 빛은 다시 collimating lens를 통과한 후 감광기(Thorlabs PDA20CS2)를 통해 측정되었다. 감광기 신호는 이후 DAQ로 전달되며 PC로 결과값이 기록된다. 버너 중심으로부터 거리별 흡광도 분포를 획득하기 위해, TDLAS 측정의 렌즈 일체와 감광기를 motorized linear stage에 설치하여 버너 중심에서부터 바깥쪽으로 2 mm 간격으로 이동하며 측정하였다. 두 collimating lens의 간격은 137 mm이었으며, 측정 위치는 버너 겉면으로부터 하류 7 mm로, 각 연소 조건별 50개의 흡수 스펙트럼을 획득하였다.

3.3. LIBS 실험 셋업

레이저 유도 플라즈마는 Nd:YAG 레이저(Nano LG300- 10, Litron Lasers)에서 조사된 레이저 펄스를 175 mm 초점 거리의 렌즈를 사용하여 공간 상 한 지점에 집중시켜 발생하였다. 레이저 duration은 6 ns이며, 에너지는 100 mJ로 고정하였다. TDLAS 측정과 동일하게, 플라즈마는 버너 겉면 하류 7 mm에 위치토록 하였다. 플라즈마에서 발생하는 발광 스펙트럼은 570 nm의 cut-on 파장을 갖는 long pass filter(Thorlabs FGL570), collimator, 광섬유, spectrometer(AvaSpec-ULS2048L)를 사용해 획득하였다. 레이저 유도 플라즈마의 발광은 수 마이크로초동안만 지속되기 때문에, delay generator(Quantum composer 9524)를 사용하여 레이저 펄스가 조사된 113.55 µs 이전부터 5 ms 동안 수집하여 분광하였다. LIBS 측정의 렌즈 일체 역시 motorized linear stage에 설치하여 버너 중심에서 반경방향으로 2 mm 간격으로 이동하며 측정할 수 있도록 하였다.

4. 측정 결과

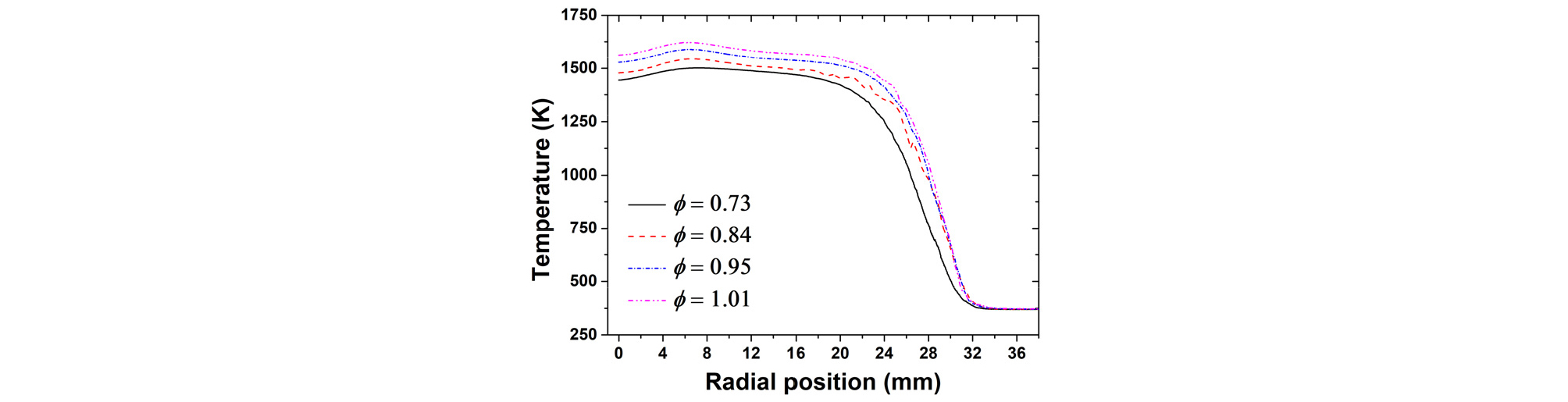
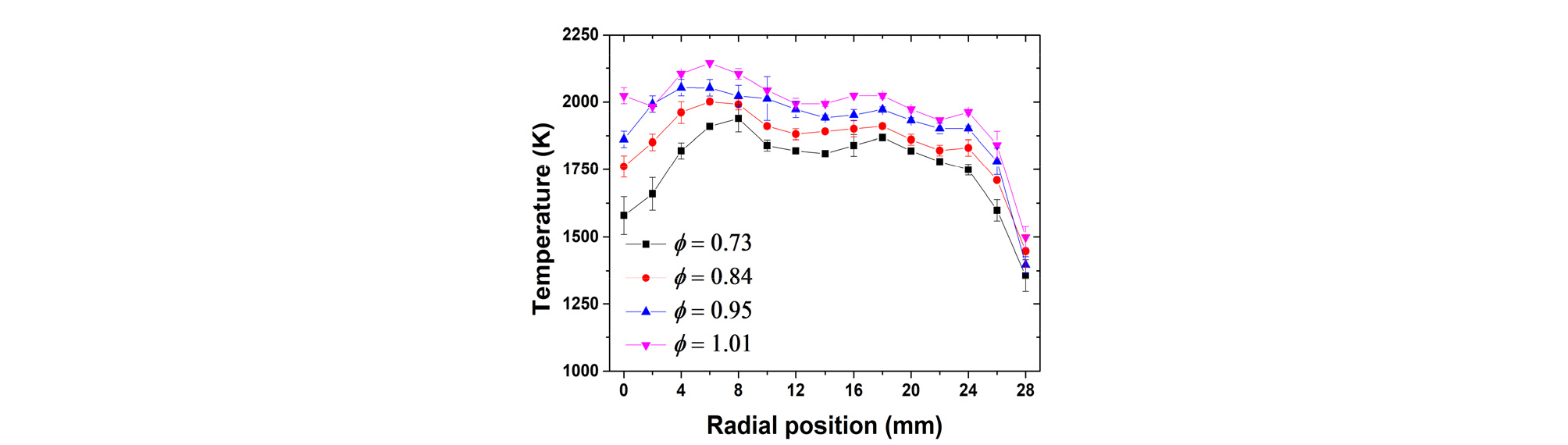
Fig. 3은 당량비를 0.73부터 1.01까지 변경해가며, type B 열전대를 사용하여 획득한 버너의 반경방향 온도 분포를 보여준다. 모든 당량비 조건에서 중심으로부터의 거리(r)가 20 mm 이내인 영역에서는 분포가 평평하게 나타났으나 연소가스가 주변 희석 공기와 혼합되는 20 mm이후부터 36 mm 영역에서는 온도가 급격하게 감소하였다. 당량비가 증가함에 따라 0 < r < 20 mm인 영역의 평균 온도는 1476 K에서 1585 K로 증가하였으며, 버너 중심은 유량 공급이 없었던 노즐 때문에 주변보다 온도가 낮았다. 제시된 온도분포는 열전대에서 일어나는 복사 열손실을 보정하지 않은 결과이며, 따라서, 광학적 측정을 통해 획득한 온도와 단열 화염 온도 대비 상당히 낮았다.

Fig. 3.

Radial temperature profiles measured by type B thermocouple for equivalence ratios from 0.73 to 1.01.

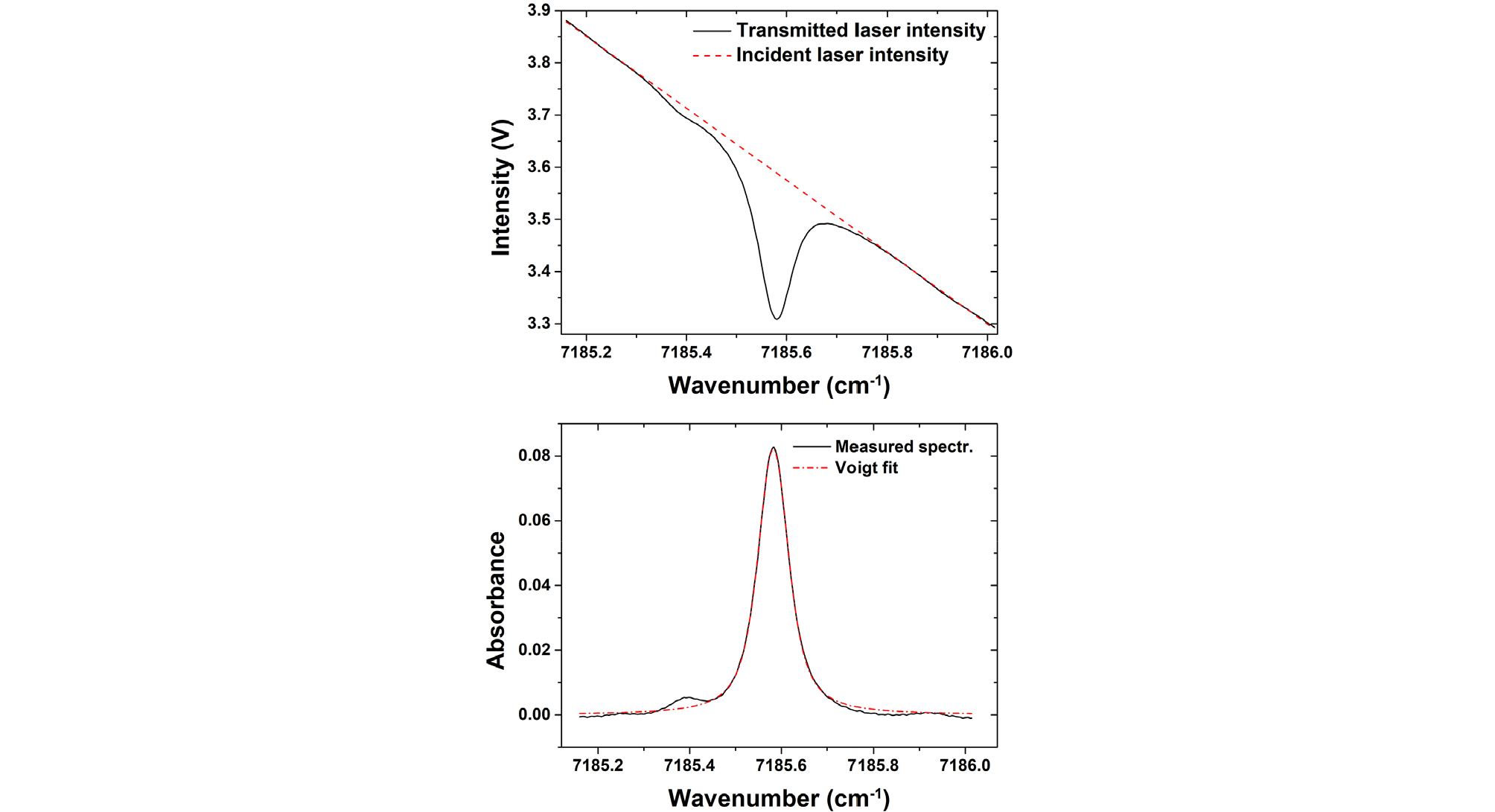
Fig. 4(a)는 7185.6 cm^-1 근방에서 파수를 선형적으로 변경시키며 획득한, 측정 영역 통과 후의 레이저 빛 세기를 보여준다. 흡광도는 식 (1)을 통해 계산되었으며, 입사 레이저 세기는 파수에 따라 선형적으로 변한다는 가정 하에 Fig. 4의 붉은 점선으로 추정하였다. 공급전류와 파장 간 변환은 실험으로부터 획득한 흡수선들의 위치를 HITRAN 2016 데이터베이스로부터 획득한 흡수선들의 위치와 맞춤으로서 이루어졌다. Fig. 4(b)는 실험 흡수 스펙트럼과 사용 흡수선의 Voigt fit을 보여준다. 측정 조건은 버너 중심을 통과하는 레이저 경로(r = 0 mm)와 당량비 0.73이다. 본 연구에서는 선모양 함수로 인한 측정 오차를 없애고자, 측정에 사용하고자 하는 7185.6 cm^-1 파수의 흡수선을 Voigt 함수로 fitting 한 후, Voigt fit의 면적을 적분하여 흡광도를 계산하였다.

Fig. 4.

(a) Transmitted and incident laser intensities near 7185.6 cm^-1. (b) Spectral absorbances near 7185.6 cm^-1 with the Voigt fit.

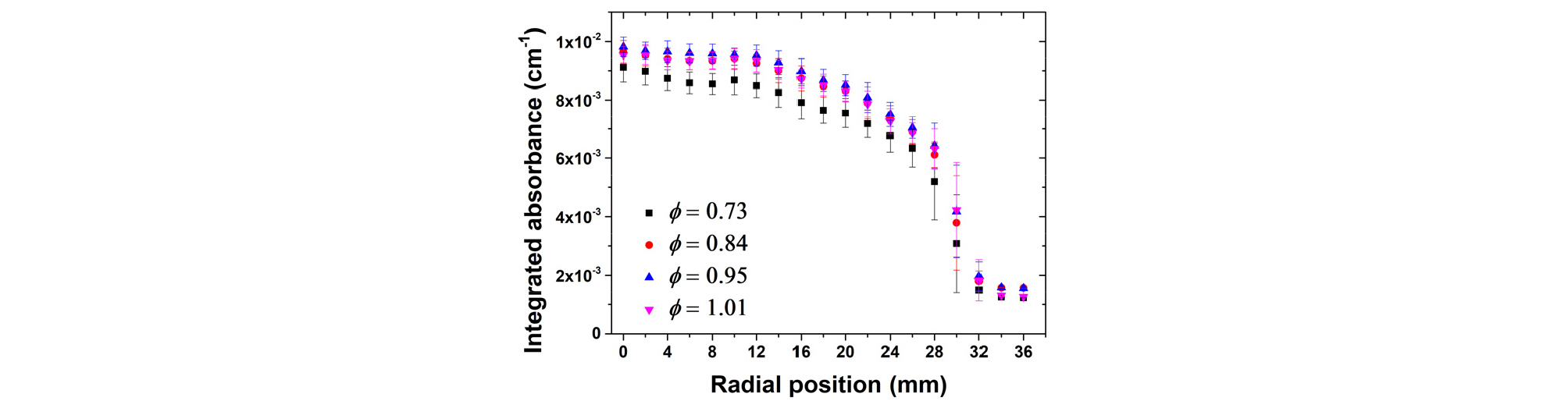
Fig. 5는 측정경로를 버너 중심에서 바깥으로 2 mm씩 이동해가며 측정한 당량비별 흡광도 분포이다. 당량비는 0.73에서 1.01로 변경하였다. 수증기의 농도는 연소가스가 발생하는 영역에서 높기 때문에 흡광도 또한 레이저 경로가 연소 영역을 더 많이 포함할수록 크게 나타났다. 한편, 흡광도는 측정경로가 버너 중심에서 벗어날수록 감소하였으나, 영(zero)으로 수렴하지 않았다. 이는 주변 공기 내의 수분(습도)이 영(zero)이 아니고 7185.6 cm^-1 파수의 선강도가 300 K에서도 유한한 값을 가지기 때문이다. 흡광도는 흡수계수의 경로 적분으로, 온도 구배, 농도 구배가 존재하는 연소장 분석을 위해서는 tomographic 재건을 진행하여야 한다. 본 연구에서는 반경방향으로 대칭인 연소장에 대해 측정을 진행하였으므로, Abel inversion[18], [19]을 통해 반경방향 흡수계수 분포를 재건하였다.

Fig. 5.

Integrated absorbances at 7185.6 cm^-1 as a function of the closest distance between the laser beam and burner axis for equivalence ratios from 0.73 to 1.01.

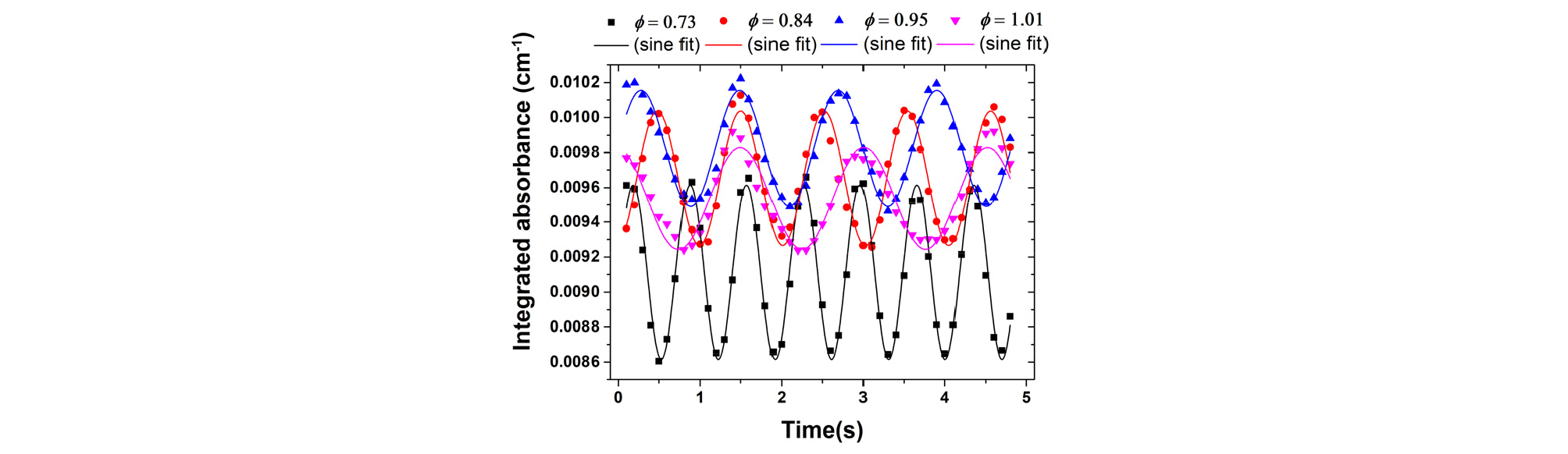
Fig. 5에서 위치별 흡광도는 중심값들로부터 상당한 편차를 보였는데, 원인 분석을 위해 시간에 따른 측정한 흡광도 변화를 분석하였다. Fig. 6은 당량비별 시간에 따른 흡광도 변화를 보여준다. 그림의 측정 조건은 각각 버너 중심을 통과하는 레이저 경로와 0.73, 0.84, 0.95, 1.01의 당량비이다. 모든 조건에서 흡광도는 사인파 형태로 진동하는 것으로 나타났다. 당량비가 변화함에 따라 진동 주파수가 변화하였으나, 동일 당량비에서 측정 위치별 주파수는 모두 동일하였다. 이러한 흡광도 진동은 연소가스가 주변 공기와 섞이면서 주기적으로 와류를 형성하여 해당 영역의 온도와 물 몰분율을 교란했기 때문으로 사료된다.

Fig. 6.

Time-varying integrated absorbances at 7185.6 cm^-1 measured at the burner center for equivalence ratios of 0.73, 0.84, 0.95, and 1.01.

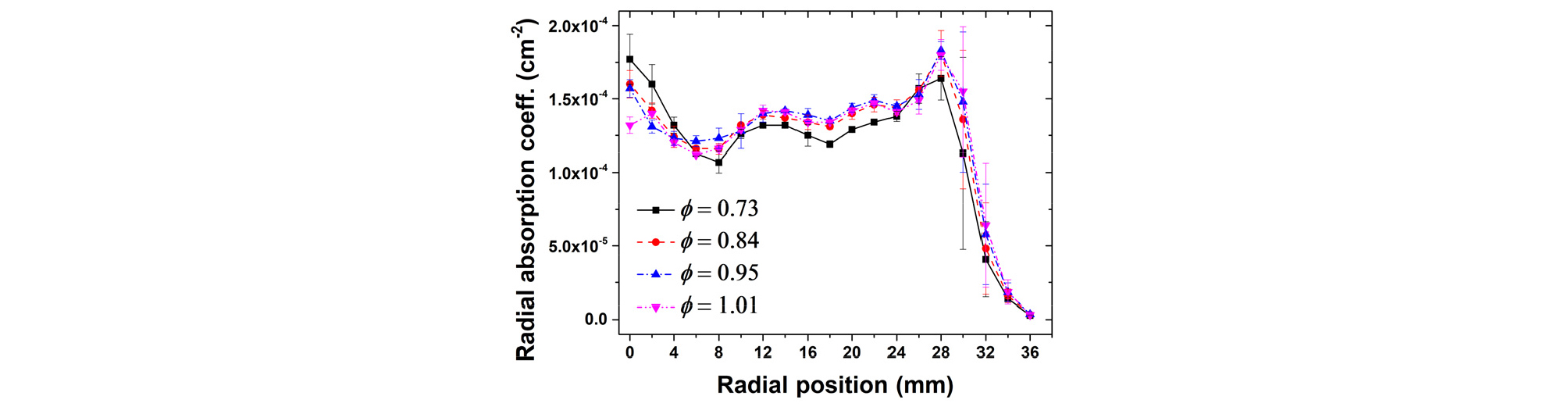
Fig. 7은 흡광도에 대한 주변 공기 습도 영향을 보정하고 서로 다른 측정 위치에서의 흡광도 진동을 위상 동기한 후, three-point Abel inversion[18], [19]을 적용하여 획득한 당량비별 반경방향 흡수계수 분포를 보여준다. 그림에서 보듯, 흡수계수의 진동은 연소가스와 주변 공기흐름이 섞이는 28 < r < 32 mm에서 크게 나타나며, 다른 영역에서는 측정 편차가 감소한다. 따라서, Fig. 5에서 보이는 편차는 TDLAS 측정 시 이 원주 부근의 온도, 농도 진동(즉, 흡광도 진동)을 경로 상 포함하기 때문이다. 모든 당량비 조건에서 흡수 계수는 r < 28 mm에서 점차 증가하고 이후 r < 36 mm에서 급격히 감소한다. 유량이 없었던 중심 노즐(r < 6 mm)에서는 주변 보다 약간 높은 흡수계수를 보였다. 당량비별 흡수계수 분포는 큰 차이를 보이지 않았는데, (흡수계수가 선강도와 측정 화학종의 몰분율에 비례함을 상기해 볼 때) 이는 당량비가 증가함에 따라 수증기 몰분율은 상승한 반면 온도는 높아져 선강도는 감소했기 때문이다.

Fig. 7.

Radial profiles of absorption coefficient reconstructed using three-point Abel inversion at 7185.6 cm^-1.

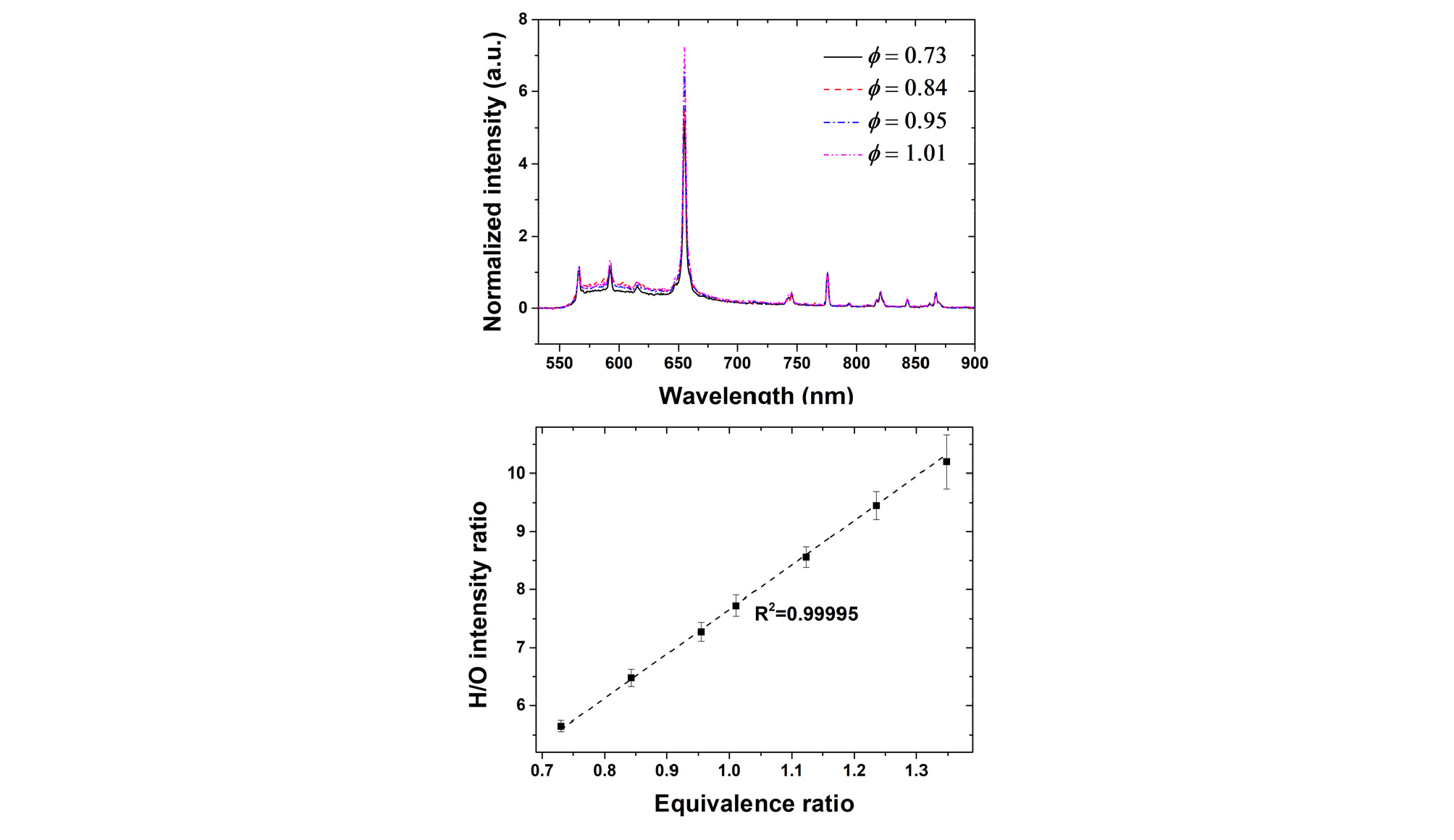
본 연구에서는 반경방향의 수증기 몰분율 분포를 구하기 위해 레이저 유도 플라즈마 발광 분광을 TDLAS와 같은 측정 평면에 대해 수행하였다. Fig. 8(a)은 당량비별 발광 스펙트럼이다. 스펙트럼은 광학 셋업에 따라 변할 수 있기 때문에 설정된 당량비에 대해서 먼저 측정을 진행하였다. 스펙트럼은 777 nm 산소원자 발광선 크기에 대해서 normalize되었으며, 당량비 변화에 따라 증가하는 656 nm 위치의 수소원자 발광선 크기를 측정하였다. Fig. 8(b)은 당량비에 따른 수소 발광선 세기와 산소 발광선 세기의 비율로 연소 온도 변화(즉, 밀도 변화)의 영향 없이 선형적 경향성이 보였으며, 해당 결과는 이미 선행연구[16]를 통해서 보고되었다.

Fig. 8.

(a) Emission spectra of laser-induced plasmas for equivalence ratios from 0.73 to 1.01. The spectra are normalized by the intensity of O (at 777 nm). (b) Ratio of H and O lineintensities within the spectra, as a function of the equivalence ratio.

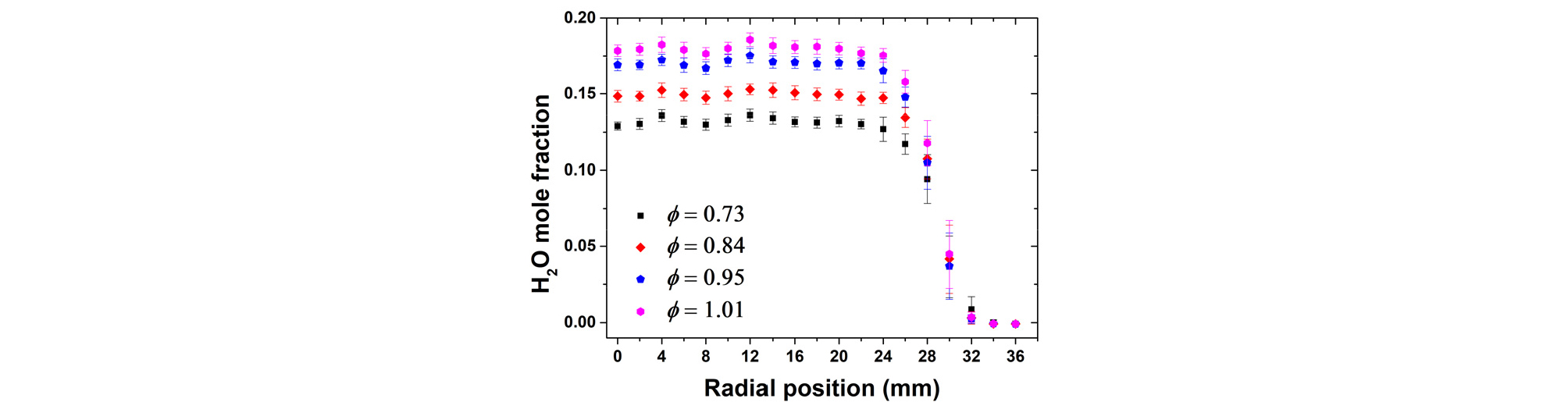
연소 시, 연료는 빠르게 물과 이산화탄소로 바뀐다. 수소, 일산화탄소, 질소산화물 등의 일부 연소 부산물들이 존재하나 이들 화학종의 농도는 1 % 미만이다. 따라서, 연소가 완료되었다고 가정하면 당량비에 따라 발생하는 수증기 몰분율은 정해지게 되며, 국부 당량비 측정을 통해 수증기 몰분율을 통해 예측할 수 있다. Fig. 9는 버너 하류 반경방향 국부 당량비 측정을 통해 획득한 운전 당량비별 수증기 몰분율 분포이다. 중심을 포함한 r < 24 mm 영역에서는 수증기 몰분율에 변화가 없이 평평하게 나타나다가 바깥으로 갈수록 급격하게 영(zero)으로 감소한다. 또한 당량비가 1에 가까워질수록 몰분율 또한 비례하여 증가한다.

Fig. 9.

Radial profiles of H₂O mole fractions obtained using LIBS for different equivalence ratios.

최종적으로 TDLAS를 통해 획득한 반경방향 흡수계수 분포와 LIBS를 통해 획득한 반경방향 수증기 몰분율 분포로부터, Fig. 10과 같이 버너 운전 당량비별 반경방향 온도 분포를 획득하였다. 식 (5)에 따라, 흡수계수를 몰분율과 전체압력으로 나누어 획득한 선강도를 HITRAN 2016 데이터베이스에서 제공하는 이론 선강도와 비교하여 온도를 특정하였다. 측정영역의 온도가 500 K 이상이므로, 선강도로부터의 온도는 500 K 이상으로 확정하였다. 모든 당량비 조건에서, 온도는 6 < r < 24 mm 구간에서는 평탄하게 나타나며 24 mm 이후 구간에서 급격히 감소한다. 중심부 r < 6 mm 영역은 중심 노즐로부터 공급 유량이 없어 온도가 약간 낮게 측정되었다. 6 < r < 24 mm 구간의 평균 온도는 당량비가 1에 가까워짐에 따라 1838 K 에서 2019 K까지 증가하였다. Cantera[20]와 GRI-Mech 3.0[21]을 사용해 계산한 단열 화염 온도(1888, 2055, 2189, 2230 K)와 비교하였을 때, 측정온도는 단열 화염 온도보다 낮았으며 그 차이는 당량비가 1에 가까울수록, 즉 온도가 높아질수록 컸다. 열전대 결과와 비교하였을 때, 측정 온도는 425 K 정도 높았다. 이는 열전대가 주변으로의 복사 열손실 그리고 열전대 와이어를 통한 전도 열손실로 인해 실제 온도보다 낮게 측정하기 때문으로 사료된다[22], [23]. 제안한 측정 방법의 반복 측정 편차는 TDLAS와 LIBS 각각의 흡수계수와 몰분율 측정 편차를 반영하여 최대 3%로 확인하였다.

Fig. 10.

Radial temperature profiles obtained based on LIBS data and TDLAS data on the spectal line at 7185.6 cm^-1.

5. 결 론

연구에서 농도 구배는 레이저 유도 플라즈마를 사용해 측정하고, 온도 구배는 측정된 농도 구배와 가변파장 레이저흡수 분광법을 사용해 획득한 흡수계수 분포로부터 측정하는 기법을 제시하였고, 반경방향으로 대칭인 연소장에 대해 성공적으로 적용하고 시연하였다. 획득한 당량비별 온도 분포는 열전대를 사용해 획득한 온도 분포와 비교해 전체 모양은 비슷하였으나, 절대 온도는 높게 측정되었다. 이는 열전대가 주변으로의 복사 열전달과 열전대 와이어를 통한 전도 열손실로 인해 온도를 낮게 측정하기 때문으로 사료된다. 제안한 측정 기법의 반복 측정 편차는 최대 3 %로 확인하였다.