1. 서 론
2. 수치 해석 방법
2.1. 촤 반응 모델
2.2. 해석 대상 및 운전 조건
2.3. 미분탄 연소 해석
3. 결 과
3.1. 실험실 규모의 연소로 해석 결과
3.2. 500 MWe 실규모 보일러의 해석 결과
4. 결 론
1. 서 론
OpenFOAM[1]은 Jasak과 Weller를 중심으로 객체지향언어인 C++를 활용하여 개발한 전산해석 프로그램이다. 오픈 소스 프로그램이므로 개발자 및 사용자 누구나가 코드 개발 및 수정이 가능하다. 또한 OpenFOAM은 무료로 배포되기 때문에 사용 시 비용 부담이 발생하지 않는다는 장점을 지닌다. 특히 대규모의 병렬 계산에 있어서 다른 상용 프로그램과 달리, OpenFOAM은 병렬 규모에 상관없이 무료로 사용 가능하다는 경제적 이점이 있다. 이밖에도 유동 및 연소 해석뿐만 아니라 구조체 응력 해석, 다상(Multiphase) 유동, DNS (Direct Numerical Simulation), 전자기장 해석 등 다양한 물리 현상을 해석할 수 있는 라이브러리가 제공되므로, 활용 가능한 범위가 매우 넓다. 이러한 장점들로 인하여 유럽에서는 대학과 기업 등에서 사용되고 있으며[2], [3], 미국과 중국, 일본 등의 세계 여러 나라에서도 사용자가 급증하고 있다. 국내에서도 국가 연구소와 대학을 중심으로 OpenFOAM에 대한 관심이 증가하고 있으며, 그 활용빈도가 점차 증가하고 있다. 본 연구진은 선행 연구를 통해 OpenFOAM을 활용하여 정상상태 미분탄 연소해석 프로그램을 개발하였으며, 대표적인 상용 전산 해석프로그램인 FLUENT와의 결과 비교를 통해 검증이 이루어졌다[4].
미분탄 연소는 탈 휘발(devolatilization), 촤 연소(char combustion) 등의 석탄 개조 반응과 가스상의 난류 연소 및 복사 열전달 등 복잡한 물리 현상이 동반된다. 특히, 촤 연소과정은 미분탄 연소과정 중 가장 느린 연소과정으로서 보일러 내 체류 시간이 길고, 대부분의 열 방출이 일어나기 때문에 미분탄 연소 해석에서 가장 중요한 요소로 여겨진다. 그리하여 선행 연구자들에 의해 많은 촤 반응 모델들이 개발 및 검증되었으며, 대표적인 모델은 kinetic/ diffusion limited 모델이다. 해당 모델은 미분탄 전산해석 모델에서 많이 사용되는 모델이지만, 반응이 진행됨에 따른 내부 구조적 변화를 고려하지 않아서 실제 촤 반응률 변화를 모사하는데 한계가 있다. 그리하여 촤 내부 구조변화에 따른 반응률을 모사하는 고유 반응률 모델들이 개발되었으며, 대표적으로는 unreacted shrinking core (USC), random pore model (RPM), char burnout kinetics extended (CBK/E) 모델들이 있다.
국내, 외 많은 연구 결과 중 해외에서는 탈휘발 모델 및 가스 반응 모델들의 영향 평가가 수행되었지만, 촤 연소 모델들에 대한 비교는 이뤄지지 않았다[5]. 국내에서는 Yang을 비롯한 연구진이 500 MW급 대항류 실규모 보일러를 대상으로 촤 반응 모델들에 대한 영향 평가를 수행하였지만, kinetic-diffusion limited 모델과 unreacted shrinking core 모델에 국한된 비교가 이루어졌다[6].
본 연구에서는 선행 연구를 통해 개발된 정상상태 OpenFOAM 연소해석 프로그램을 바탕으로 대표적인 촤 고유 반응률 모델인 USC, RPM, CBK/E 모델을 OpenFOAM에 구현하였다. 구현된 모델을 바탕으로 파일럿 규모의 연소로에 적용하여 실험 결과와의 비교를 통해 촤 반응 모델 비교를 수행하였다. 더불어 500 MWe 실규모 연소로에 적용하여서 보일러 내부 변화의 고찰을 통해 촤 고유 반응률 모델들을 비교하였다.
2. 수치 해석 방법
2.1. 촤 반응 모델
2.1.1. Kinetic-diffusion limited model
Field[7] 등은 diffusion limited 모델의 단점을 보완하고자 새로운 모델을 개발하였으며, 촤 반응 속도()는 다음 식과 같이 표현된다.
| $$R_c=\left(\frac{k_dk_c}{k_d+k_c}\right)P_{O_2}$$ | (1) |
식 (1)은 일반적인 연소 상황에서 촤의 반응을 잘 모사한다고 알려져 널리 사용되고 있지만, DTF(Drop Tube Furnace) 실험[8], [9] 등을 통해 반응 상수를 획득해야 한다. 또한 반응이 진행됨에 따른 미분탄 내부 구조 변화 등을 물리적으로 기술하지 못하는 단점이 있다.
2.1.2. Unreacted shrinking core model
촤의 구조를 unreacted core와 core 주변을 반응이 일어나지 않는 다공성 구조를 지닌 회분층으로 가정하여 촤 반응 속도를 예측하는 촤 반응 모델이 Wen[10]에 의해 발표되었다. 해당 모델은 주변 공기의 확산 및 확산된 공기의 회분 층 내부 확산속도, 그리고 내부의 core 표면에서의 화학 반응 속도를 통해 촤 반응 속도가 결정된다고 가정하며, 촤 반응 속도는 다음과 같다.
| $$R_c=\frac1{\frac1{k_{diff}}+\frac1{k_{surface}Y^2}+\frac1{k_{ash}}\left(\frac1Y-1\right)}P_{O_2}$$ | (2) |
주변 가스의 확산속도(), 표면에서의 화학 반응 속도(), 회분 층 내부 확산속도() 각각의 반응 상수가 요구되며, 각 반응 상수는 선행 연구의 값을 참조하였다[6].
2.1.3. Random pore model
Bhatia와 Perlmutter는 촤 내부 구조를 원통 형태의 내부 기공을 가진 다공성 구조로 가정하고, 촤 반응이 진행됨에 따라 촤 내부의 기공이 커지며 병합되는 과정을 통해 촤 반응 속도를 모사하는 촤 반응 모델을 제안하였다[11]. 반응 속도는 식 (3)으로 표현되는 촤 내부 기공구조와 전환률에 따른 촤 반응면적과의 관계식으로 나타내어지며, 화학 반응 속도는 식 (4)로 표현된다.
| $$\Psi=4\pi L_0(1-\epsilon_0)/S_0^2$$ | (3) |
| $$R_c=k_cP_{O_2,s}^n\times\sqrt{1-\Psi\ln\left(\frac{M_c}{M_{c,0}}\right)}$$ | (4) |
| $$R_{diff}=k_d(P_{O_2}-P_{O_2,\;s})$$ | (5) |
주변 가스로부터 촤 내부의 확산속도가 촤 전체 화학 반응 속도가 균형을 이뤄야 하므로, 식 (4)와 식 (5)가 같게 되는 촤 표면분압()을 Brent method[12]를 통해 구한 뒤 해당 산소분압 값을 활용하여 촤 반응률을 얻게 된다.
앞선 두 모델과 마찬가지로 활성화 에너지(E) 및 빈도 상수(A) 값이 요구되며, 더불어 촤 내부에 대한 측정값을 바탕으로 내부 기공구조(Pore structure) 상수() 값을 획득해야 한다. 반응 상수와 내부 구조를 표현하는 식 (3)의 상수 값은 선행 문헌의 값을 참조하였다[13].
2.1.4. Char burnout kinetics (CBK/E)
Hurt와 Calo는 미분탄 연소가 진행됨에 따라 버너 주변에서의 초기 반응 속도보다 연소로 후단부에서의 촤 반응 속도가 느리다는 실험 결과를 바탕으로 촤 반응 정도에 따른 촤 반응 속도를 예측하는 모델을 제안하였다[14].
연소가 진행됨에 따른 반응 속도가 감소하는 물리적 현상을 반영하기 위해 총 4개의 추가 모델을 도입하였다. 먼저 single film char oxidation 모델은 촤 입자 주변에서의 확산 반응 및 화학 반응을 모사하는 것을 나타내며, thermal char deactivation 모델은 다공성의 촤 구조가 고온에 의한 annealing 효과로 인해 다공성이 감소하여 반응성이 감소함을 나타낸다. 다음으로 ash inhibition 모델은 촤 내부에 기 보유된 회가 연소과정을 거치며 촤 주변에 부착하여 반응성을 감소하는 효과를 모사하는 모델이다. 마지막으로 char physical property 모델은 연소과정이 진행되면서 촤 밀도 및 크기 등의 물성이 변화하는 것을 나타낸다.
앞선 모델들을 종합하여 촤 내부에서 발생하는 총괄 반응식은 아래와 같이 3단계 반응식으로 요약하여 나타낼 수 있다.
| $$C\;\;+\;\;O_2\;\rightarrow\;\;2C(O)\\C(O)\;\;+\;\;O_2\;\;\rightarrow\;\;CO_2\;\;+\;\;C(O)\\C(O)\;\;\rightarrow\;\;CO$$ | (6) |
식 (6)의 단계별 반응 속도를 각각 , , 으로 표기하고, 아레니우스 반응식으로 모사된다. 이때 빈도 상수 중 A3은 DAF(Dry Ash Free) 기준의 탄소 분율 값(CDAF)을 활용하여 계산된다. 나머지 빈도 상수 및 활성화 에너지는 Table 1에 명시된 상관관계를 통해 계산된 값을 이용한다. 앞선 단계별 반응 속도를 활용하여 촤 입자 주변의 전체 산화율()은 식 (7)을 통해 얻을 수 있으며, 이때 CO와 CO2의생성비는 식 (8)의 관계로 나타내어진다.
| $$r_{gas}=\frac{k_1k_2P_{O_2,s}^2+k_1k_3P_{O_2,s}}{k_1P_{O_2,s}+k_3/2}$$ | (7) |
| $$\frac{CO}{CO_2}=\frac{k_3}{k_2P_{O_2,s}}$$ | (8) |
Table 1. Rate constants
| A3 | sec-1 | E1 | 25 kJ/mol |
| A2/A3 | (mol/cm3)-1 | E2 | 117 kJ/mol |
| A3/A1 | (mol/cm3)-1 | E3 | 133.8 kJ/mol |
Generalized Thiele modulus를 이용한 유효인자와 앞서 획득한 전체 산화율과의 곱을 통해 촤 화학 반응 속도를 획득한다[15], [16]. 이후 Brent method를 활용하여 계산된 촤 표면 분압을 통해 촤 반응률을 얻게 된다.
2.2. 해석 대상 및 운전 조건
2.2.1. 2.1 MWe 실험실 규모 연소로
측정 위치별 온도 및 화학종 분포가 상세히 주어지는 IFRF (International Flame Research Foundation) MMF 5-2 화염[17]을 해석 대상으로 선정하였다. Fig. 1은 IFRF no.1 연소로 형상을 나타낸 것이며, 연소로의 축 방향으로는 6.25 m이고, 가로, 세로 2 m의 정사각형 단면으로 구성되어 있다. 연소로 외부에는 총 7개의 cooling loop가 설치되어 있으며, 연소로 내부로는 총 5개의 위치에서 측정이 이루어졌다.
버너는 air staged burner로서, 263 kg/h 미분탄이 1차 유입구를 통해 공급된다. 1, 2차 공기 유입량은 각각 421 kg/h, 2,670 kg/h이며, 2차 공기는 유입구 전단에 설치된 스월러로 인해 약 0.9의 스월비를 가진다. 미분탄 입자는 평균 60 µm의 크기를 가지며, 최소 10 µm, 최대 150 µm, 1.13의 형상 지수를 가진 rosin-rammler 분포를 적용하였다. 미분탄 성상은 Table 2에 상세히 나타나 있다. 전산해석 부담을 줄이고자 1/4 형상에 대한 전산해석을 수행하였다. 전산해석 격자는 약 42만개의 정렬 격자로 구성하였으며, 약 1,500개의 parcel을 활용하여 입자 거동을 모사하였다.
Table 2. Coal properties
| Proximate analysis (wt%, as fired) | Ultimate analysis (wt%, Daf) | ||
| Volatile | 37 | C | 79.3 |
| Fixed Carbon | 52.5 | H | 4.7 |
| Ash | 8.3 | O | 13.7 |
| Moisture | 2.0 | N | 1.3 |
| S | 1.0 | ||
| Coal LCV (J/kg) | 2.918 e+07 | ||
2.2.2. 500 MWe 실규모 연소로
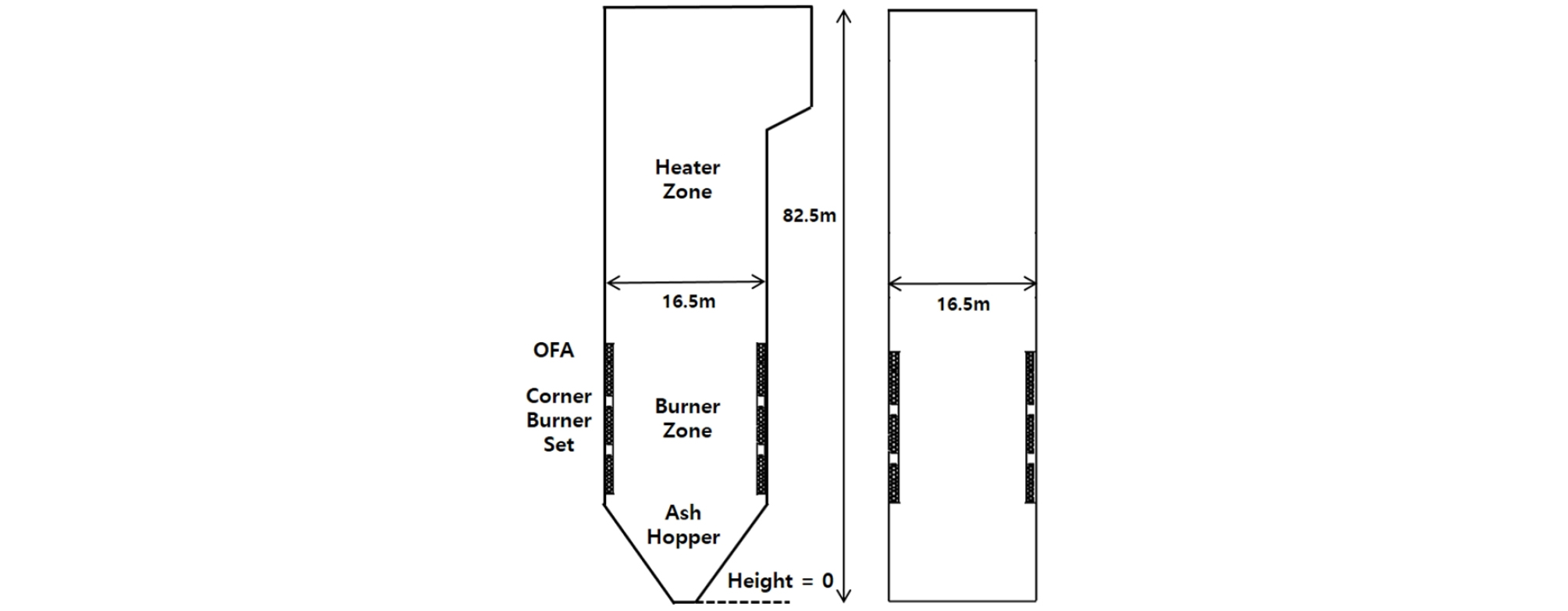
Fig. 2는 해석에 사용된 500 MWe급 접선형 미분탄 보일러의 구조를 나타낸 것이다. 각 코너별 총 6개의 버너 세트로 구성되어 있으며, 각 버너 영역 상부에 설치된 over-fire air(OFA)를 통해 추가 연소 공기가 공급된다. 운전 조건과 미분탄 성상은 각각 Table 3과 4에 상세히 나타나 있다.
Table 3. Operating conditions
| Mass flow rate | Temp. | |
| Pulverized Coal | 172310 kg/h | 355 K |
| Primary Air | 344100 kg/h | 355 K |
| Secondary Air | 1292700 kg/h | 588 K |
Table 4. Coal properties
| Proximate analysis (wt%, as fired) | Ultimate analysis (wt%, Daf) | ||
| Volatile | 28 | C | 82.0 |
| Fixed Carbon | 52 | H | 5.1 |
| Ash | 15 | O | 10.3 |
| Moisture | 5 | N | 1.7 |
| S | 0.9 | ||
| Coal HCV (J/kg) | 2.646 e+07 | ||
전열부는 총 5개의 과열기와 재열기로 구성되었으며, 본 연구에서는 해당 부분을 다공성 매체(porous media)로 가정하였다. 다공성 매체를 통해 각 전열부에서의 열 흡수량 및 압력 저하를 통한 운동량 저하를 모사하였다. 미분탄 입자는 평균 63 µm 의 크기를 가지며, 최소 10 µm, 최대 150 µm, 1.13의 형상 지수를 가진 rosin-rammler 분포를 적용하였다. 전산해석 격자는 약 330만개의 정렬 격자로 구성되었다. 입자는 약 15,000개의 parcel을 활용하여 입자 거동을 모사하였다.
2.3. 미분탄 연소 해석
난류 모델은 standard k-ε 모델을 사용하였으며, 복사 모델은 탄화수소 계열의 연소시 광학두께(optical thickness)가 1보다 큰 것을 고려하는 P1 모델로 선정하였다. 또한 기체의 흡수계수에 있어서 CO2와 H2O 몰 농도에 따른 흡수계수의 변화를 고려한 회색기체가중합법(weighted sum of gray gases model)을 적용하였으며, 미분탄 입자의 복사 참여를 고려하였다. 난류 연소 모델은 화학 평형을 가정하여 난류 혼합속도에 의해 전체 연소 속도를 결정하는 EDM(Eddy Dissipation Model)을 적용하였다. 반응식으로는 Westbrook에 의해 제안된 탄화수소의 2단계 총괄 반응식(2-step global kinetic mechanism)을 적용하였다. 기체로부터의 입자의 열전달은 Ranz-Marshall 관계식으로 모사하였다[18]. 난류에 의한 입자 확산의 영향을 고려할 수 있도록 Gosman과 Ioannides에 의해 제안된 stochastic 기법이 적용되었다[19]. 미분탄 탈 휘발과정은 single-step 모델로 구현되었다. 수치 확산의 저감을 위하여 2nd order upwind 기법이 적용되었다.
3. 결 과
3.1. 실험실 규모의 연소로 해석 결과
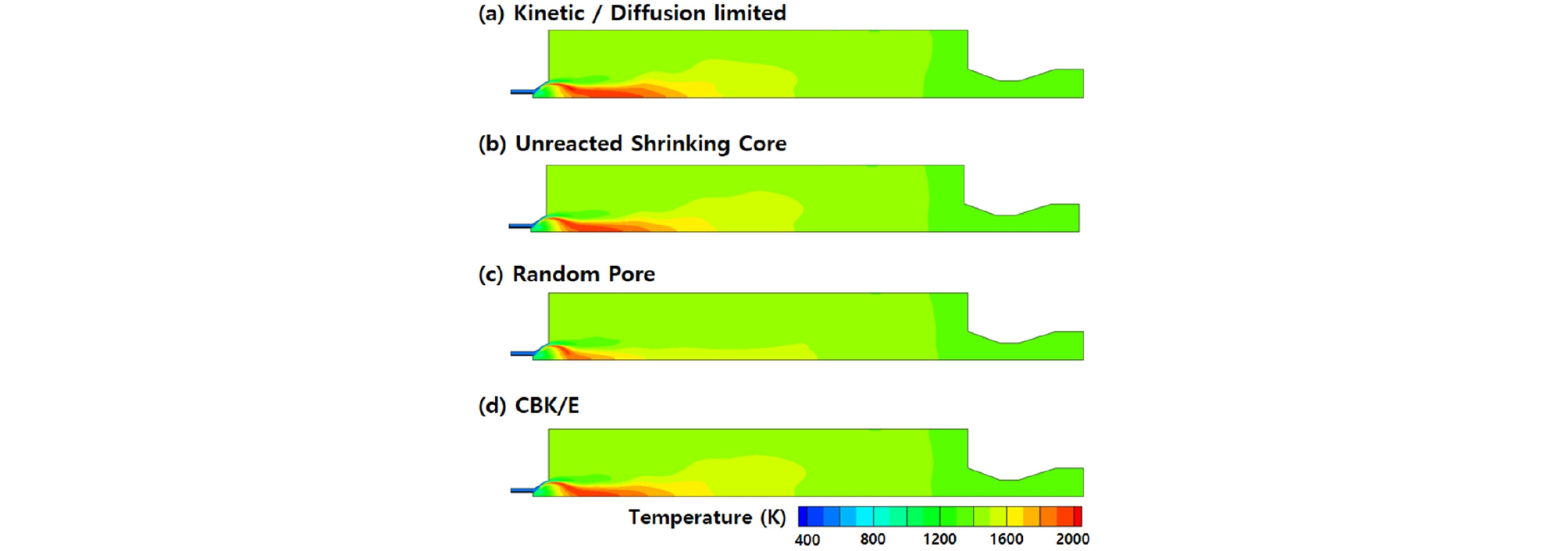
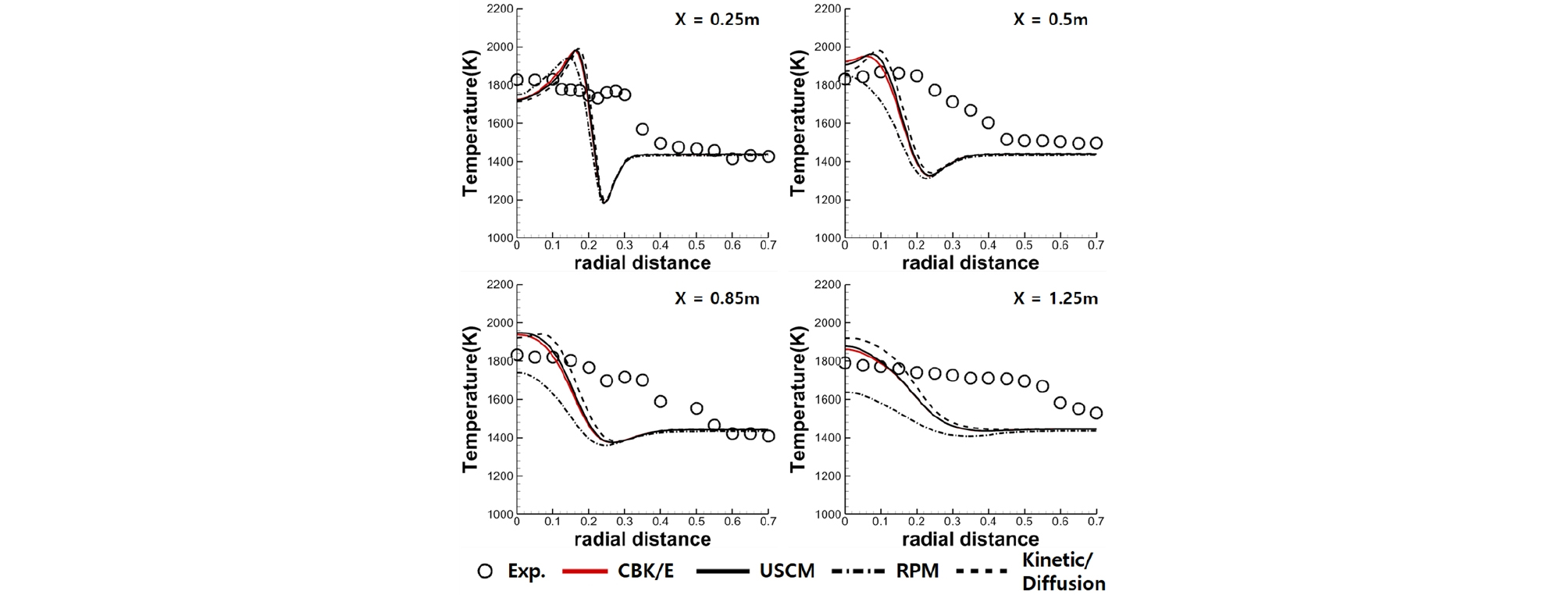
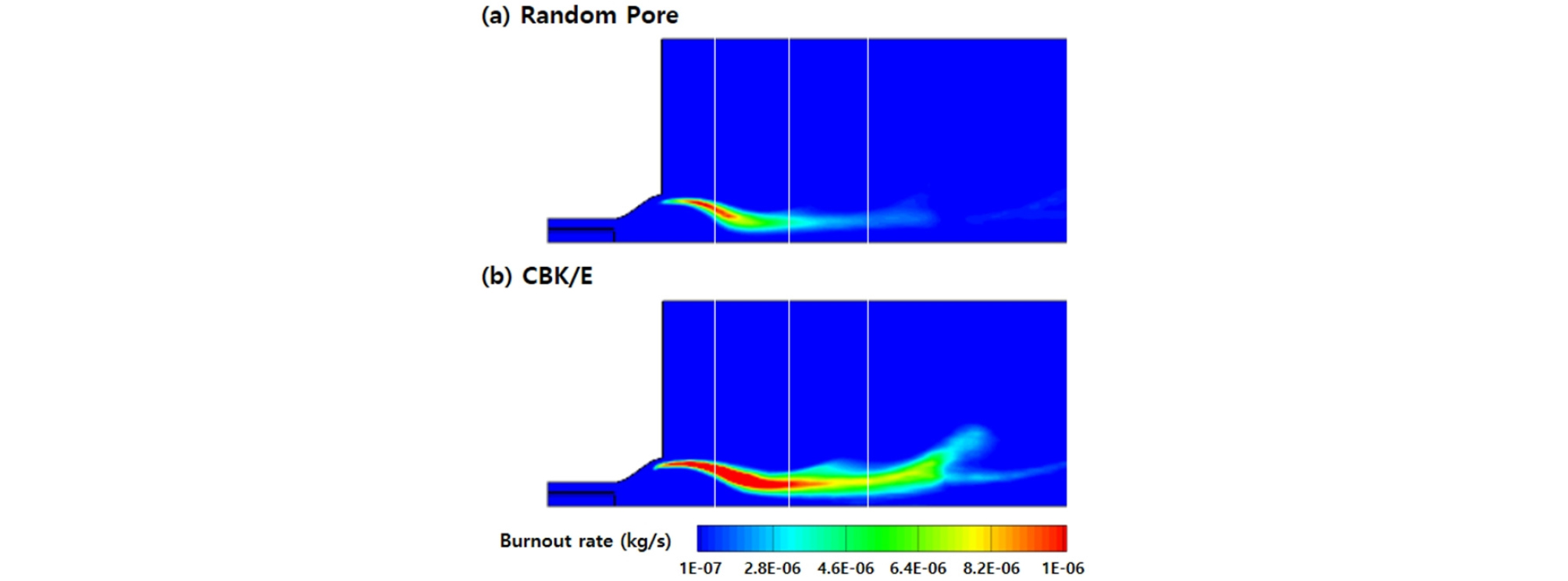
Fig. 3은 촤 반응 모델에 따른 연소로 내부 온도 분포 결과를 나타낸 것이다. Random pore 모델을 제외한 다른 모델들 결과에서는 큰 차이를 보이지 않음을 확인하였다. Kinetic/diffusion limited 모델의 경우 연소로 반응을 잘 모사할 수 있도록 문헌에서 제공된 반응 상수를 사용하여서, 다른 촤 고유 반응 모델의 결과와 큰 차이를 보이지 않는 것으로 생각된다. Fig. 4는 각 위치별 측정된 반경 방향 데이터와 해석 결과를 비교한 것이다. X=0.25 m 영역은 탈 휘발 종료 후 촤 연소가 시작되는 부분으로 많은 촤 연소 반응이 일어나지 않았기 때문에 온도 분포에서 큰 차이를 보이지 않는다. 그러나 연소로 하단부로 갈수록 random pore 모델을 이용한 해석 결과가 낮은 가스 온도를 예측함을 알 수 있다. 이는 random pore 모델이 다른 모델과 다른 촤 반응 속도를 예측함에 기인하였다고 생각된다. Fig. 5는 버너 주변에서의 촤 반응 속도를 비교한 것이다. Random pore 모델의 경우 CBK/E 모델보다 낮은 촤 반응 속도를 예측하는 것을 알 수 있다. 그리하여 random pore 모델은 낮은 촤 반응 속도를 예측함으로써 버너 부근의 적은 열 방출로 인해 연소로 하단부로 갈수록 낮은 가스 온도를 예측하는 것으로 생각된다.
Random pore 모델에서의 낮은 온도 예측 결과는 두 가지 요인에 의한 결과로 생각된다. 하나는 대상 연소로의 운전 조건이 모델 사용에 적합한 운전 조건과의 차이에 오는 것이며, 다른 하나는 모델에 사용된 반응 상수가 실제 운전을 대변하지 못하는 것으로 생각된다. 촤 연소 메커니즘은 산소 확산속도와 화학 반응 속도 크기에 따라 3단계로 구분되며[20], 이 중 random pore 모델은 입자 내부까지 산소가 충분히 확산되어 화학 반응 속도가 전체 반응 속도를 지배하는 저온 영역 Zone Ⅰ ~ Ⅱ에 주로 적용되었다[21]. 그러나 대상 연소로는 고온 영역에서 촤 반응이 진행되므로 화학 반응 속도가 매우 빨라서 산소가 표면에 도달하면서 반응이 진행되는 Zone Ⅲ 영역에 해당한다고 볼 수 있다. 연소가 활발히 이뤄지는 고온 영역에는 random pore 모델의 예측이 정확히 이뤄지지 않는 것으로 생각된다.
본 연구에서 사용된 반응 상수(A, E) 및 입자 내부 기공구조 상수()는 가스화 조건에서 획득한 선행 연구 결과를 사용하고 있다[13]. Random pore 모델 사용을 위해 필요한 인자인 내부 기공구조 상수는 촤 반응 속도 예측에 영향을 주며, 해당 상수 값에 따라 촤 반응 속도 예측에 있어 차이를 보임을 선행 연구에서 밝혀졌다[22]. 해당 상수 값을 결정하기 위해서는 촤 내부 구조를 대변하는 각종 인자들이 요구되는데, 해당 인자들은 mercury porosimetry 및 gas adsorption, computer controlled scanning electron microscopy(CCSEM)과 같은 각종 실험 및 영상 분석을 통해 얻어야 한다[23]. 그러나 본 연구에서는 앞서 언급된 실험 등을 통해 촤 내부 구조를 파악하는데 제약이 있어서 정확한 입자 내부 기공구조 상수 값을 사용하지 못하였다. 추후 입자 내부 기공구조의 정확한 값을 획득하면 보다 정확도 높은 예측이 이루어질 것으로 생각된다.
3.2. 500 MWe 실규모 보일러의 해석 결과
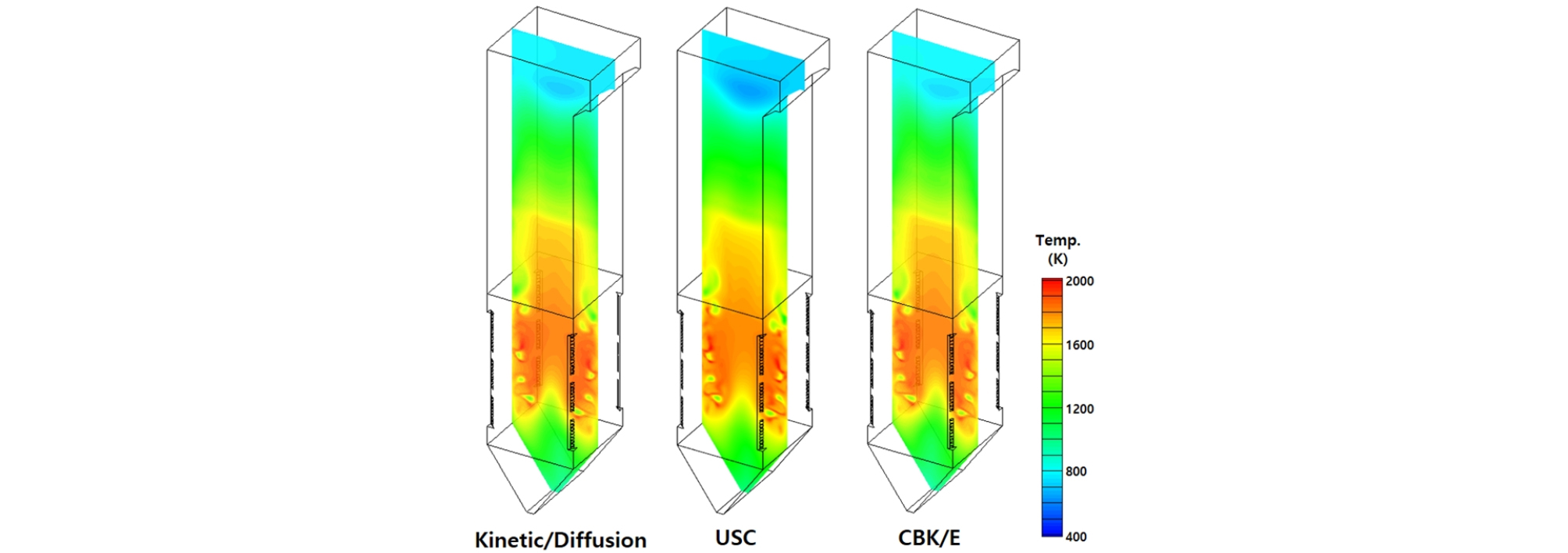
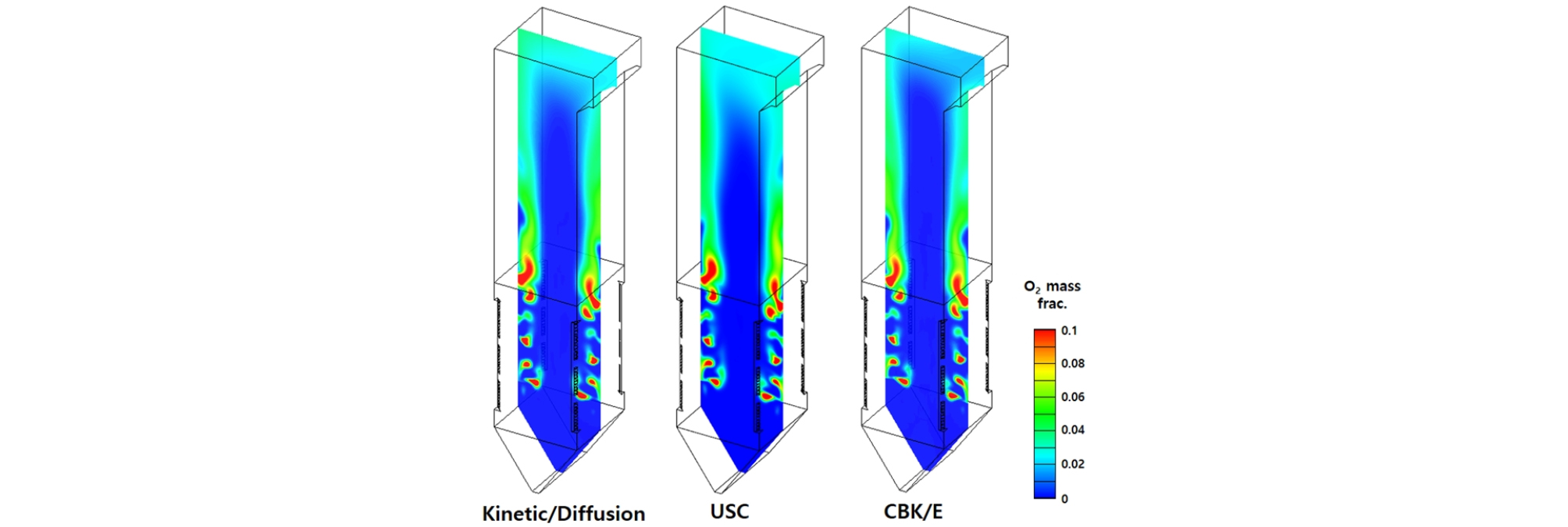
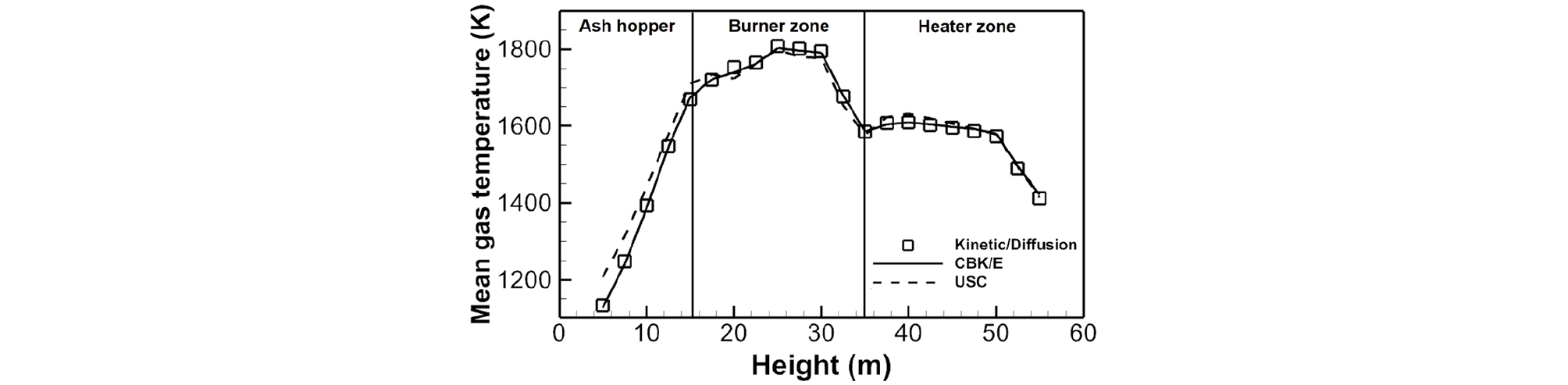
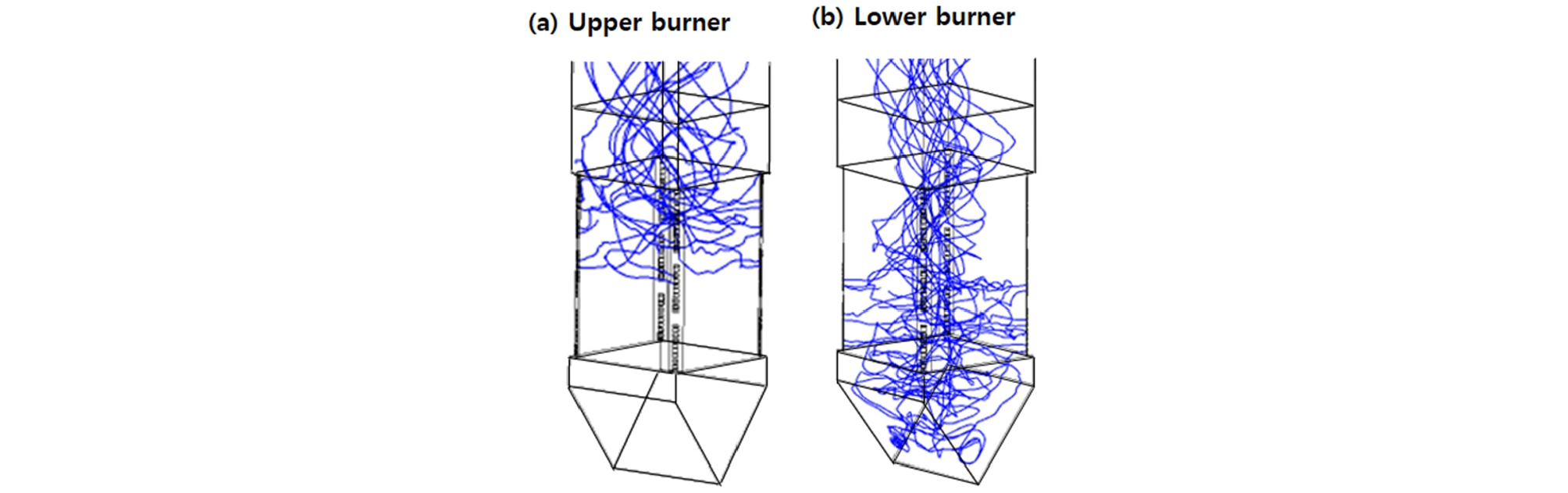
앞서 실험실 규모의 연소로 결과를 바탕으로 연소 범위에 적합한 모델과 해당 모델 사용에 있어 적절한 반응 상수가 주어져야 함을 확인하였다. 그리하여 random pore 모델을 제외한 다른 촤 반응 모델을 500 MWe 실규모 보일러에 적용하였다. Fig. 6과 7은 촤 반응 모델에 따른 보일러 내부 온도 및 산소 농도 분포를 나타낸 결과이다. 실험실 규모의 연소로보다 훨씬 긴 체류 시간을 가진 실규모 보일러에서도 각 모델에 따른 평균 온도 및 산소 농도 분포에서 큰 차이를 확인하지 못하였다. 이를 통해 촤 연소 과정을 대변할 수 있는 모델 상수를 사용할 경우 kinetic/diffusion limited 모델도 촤 고유 반응률 모델에 근접한 결과를 예측할 수 있음을 확인하였다. Fig. 8은 보일러 높이별 평균 가스 온도 분포를 비교한 결과를 나타낸다. 버너 근처의 고온 영역에서는 열 교환기 부분에 있어 단면 평균 가스 온도 결과는 촤 반응 모델에 따라 큰 차이를 보이지 않음을 확인하였다. 이는 버너 영역에서 형성된 고온으로 인해 버너 및 전열부에서는 ZoneⅢ에 해당하여 대부분의 열 방출이 일어나기 때문에 해당 영역에서 촤 반응 모델에 따른 큰 차이를 보이지 않는 것으로 생각된다. 그러나, 보일러 하부에서 USC 모델 결과가 다소 높은 가스 온도를 예측함을 알 수 있다. Fig. 9에서 보는 바와 같이 하단부 버너에서 투입된 미분탄은 보일러 하부로 향하는 유동을 따라 ash hopper 부근까지 내려가 선회하며 연소로 상단부로 향하게 되는 거동을 보인다. 이때 random pore 모델은 다른 모델과 달리 ash hopper 영역에서 보다 많은 촤 반응을 예측함으로써 다소 높은 가스 온도 결과를 보이는 것으로 생각된다.
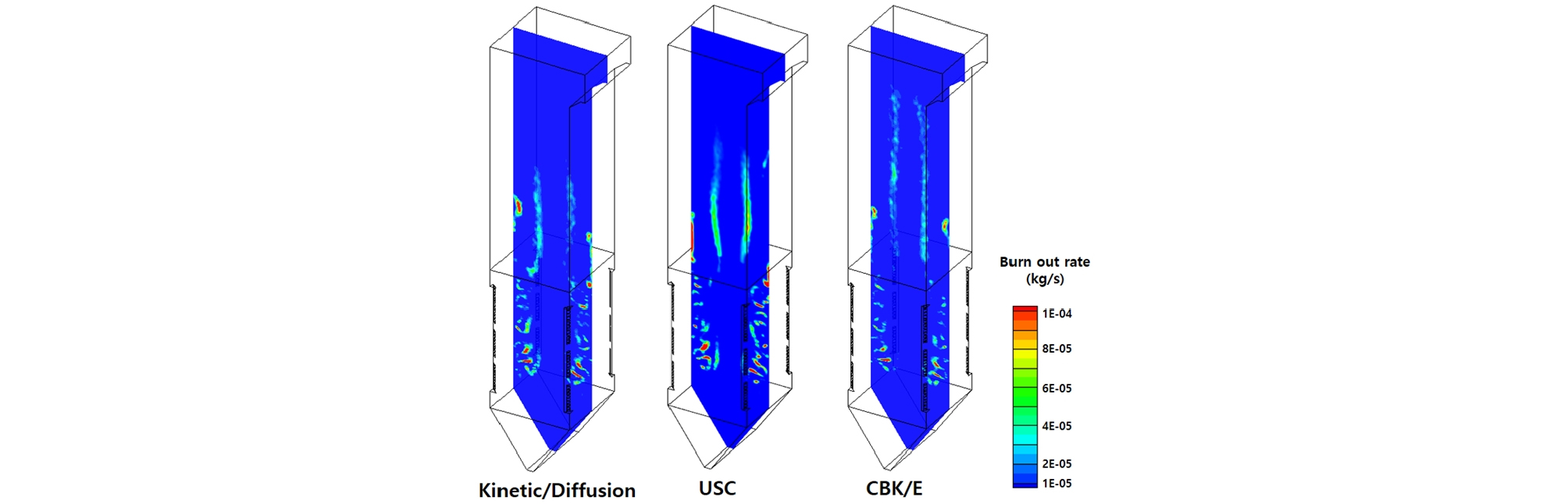
Fig. 10은 연소로 내부에서의 촤 반응 속도를 비교한 것이다. USC 모델에서는 촤 반응이 진행됨에 따라 촤 코어 크기 감소 및 회분 층의 확산 속도 변화 등을 고려하기 때문에 kinetic/diffusion limited 모델에 비해서 연소로 상단부까지 촤 반응이 예측되며, 이는 선행 연구 결과와 같은 결과를 예측한다[6]. CBK/E 모델의 경우는 미분탄 연소 점화 및 소염에 이르는 전 영역에 대한 모사가 가능하며, 또한 촤 연소가 진행됨에 따라 회분층 증가 및 물성치 변화 등을 모사할 수 있기 때문에 각 모델 중 연소로 최상부까지 촤 반응 속도를 예측함을 알 수 있다. 연소가 진행됨에 따른 촤 반응 속도 변화를 모사하기 제한되는 kinetic/diffusion limited 모델보다 촤 고유 반응 모델인 USC모델과 CBK/E 모델이 나은 결과를 예측하는 것으로 생각된다. 따라서 보일러 내부 연소 최적화뿐만이 아니라 슬래깅(slagging) 및 파울링(fouling)등의 미분탄의 연소 진행 상황에 따른 입자 크기 및 특성 변화를 고려해야 하는 전산해석에서는 kinetic/diffusion limited 모델보다 촤 고유 반응 모델들을 선택하는 것이 나은 결과를 예측할 것으로 생각된다. 또한 촤 고유 반응 모델 중 점화부터 소염에 이르는 전 영역에서의 입자 변화를 모사할 수 있으며, DAF 기준의 탄소 분율 만을 가지고 손쉽게 반응 상수를 획득할 수 있는 장점을 지닌 CBK/E 모델을 사용하는 것이 보다 쉽고, 정확한 예측 결과를 얻을 수 있을 것으로 생각된다.
4. 결 론
본 연구에서는 OpenFOAM을 활용하여 기존에 제공되는 kinetic-diffusion limited 모델 이외에 대표적인 촤 고유 반응률 모델인 unreacted shrinking core 모델, random pore 모델, char burnout kinetics extended 모델을 구현하였다. 이를 바탕으로 2.1 MWe 실험실 규모의 연소로와 500 MWe 접선 연소식 실규모 보일러를 대상으로 구현된 촤 연소 모델에 대한 영향 평가를 수행하였다.
실험실 규모의 연소로에 대해서는 random pore 모델을 제외한 각 모델 간에 큰 차이를 보이지 않았다. Random pore 모델의 경우, 모델 적용에 적합한 연소 환경과 적절한 반응 상수가 주어지면 보다 나은 예측이 이루어질 것으로 생각된다.
실규모 연소로에서는 전반적으로 모델 간 차이가 확인되지 않았으며 연소로 하단부에서 USC 모델이 빠른 촤 반응 속도를 예측함을 확인하였다. 더불어 슬래깅과 파울링 같은 미분탄 특성에 대한 정확도 높은 해석이 이루어지기 위해서는 촤 고유 반응 모델을 사용해야 할 것으로 판단되며, CBK/E 모델은 반응 상수 획득을 위한 추가 실험 없이 해당 탄종의 원소 분석 결과만으로 쉽고 정확한 예측이 이루어질 것으로 생각된다.