1. 서 론
2. 실험장치 및 측정방법
2.1. 실험장치
2.2. 실험 및 측정방법
3. 실험결과 및 검토
3.1. 이론모델 및 반응메커니즘의 검증
3.2. SNG 연료의 와 lb
4. 결 론
1. 서 론
지속적인 에너지 소비증가로 인한 에너지 부족현상과 기후변화 문제가 심각해지고 있는 가운데 재생에너지(renewable energy) 및 대체에너지(alternative energy)에 대한 관심이 지속적으로 증가하고 있으며, 새로운 에너지(advance energy)에 관한 연구가 수행되어왔다. 특히, 가격상승 정도가 비교적 작고 매장량이 풍부한 석탄을 이용한 가스화(coal gasification) 기술이 주목을 받고 있다. 석탄 가스화 공정을 거친 결과물 중 하나인 합성천연가스(Synthetic Natural Gas, 이하 SNG)는 메탄(CH4)을 주성분으로 가지고 있어 천연가스 연료를 대체할 수 있을 것으로 예상된다[1], [2]. 그러나 이러한 대체연료들은 기존 연료와는 다른 성분을 포함하고 있어 연소특성이 다르게 나타날 것으로 예측된다. 따라서 기존 연료에 맞춰 설계된 연소기에 대체연료를 사용하기에 앞서 SNG 연료의 연소특성을 파악하는 것이 필요하다[2].
한편, 1차원 예혼합 화염에서 화염 면에 수직 방향으로 미연혼합기(unburned mixture)가 전파하는 속도로 정의되는 층류연소속도(laminar burning velocity)는 예혼합 연료의 연소특성 중 하나로써 당량비 및 연료조성과 관련된 물성치이며, 연소율(burning rate) 및 화염의 날림(blow off)이나 역화(flash back)같은 실제 연소현상을 이해하는데 중요한 인자이다[3], [4]. 이 경우 정확한 층류연소속도를 측정하는 것이 화학반응 메커니즘의 개발과 검증에 큰 역할을 한다[5]. 또한 굴곡진 국부화염대 신장(stretch)에 대한 특성변수인 마크스타인 길이(Markstein length)는 스트레치율(stretch rate)에 대한 화염속도의 반응으로 정의되며, 스트레치를 받은 화염의 거동을 보다 정확히 특성화 하는데 필요한 변수이다. 마크스타인 길이는 특정 예혼합 난류화염 모델에서 기초적인 물리 화학적 인자이기 때문에 이를 정확히 측정하는 것이 요구된다[6], [7].
이러한 층류연소속도와 마크스타인 길이를 실험적으로 측정하기 위한 방법들이 지속적으로 개발 및 발전되어 왔다. 층류연소속도를 측정하는 대표적인 방법에는 분젠 버너에서 슐리렌(schlieren) 이미지를 이용하는 방법, 대향류 화염을 이용하는 방법, 평면 화염을 이용하여 연소기의 표면온도를 측정하는 방법, 구형으로 전파하는 화염을 이용하여 측정하는 방법 등이 있다[8], [9]. 이러한 방법들 중에서 특히 구형 전파화염 방법은 표면에서 발생하는 셀 불안정성(cellular instability) 관측이 가능하고 고압과 다양한 초기 온도조건에서 실험이 용이하며, 고압조건에서는 유동에 의한 화염 불안정성이 현저히 적기 때문에 보다 정확한 층류연소속도를 측정할 수 있다는 장점이 있다[9].
구형 전파화염에서 층류연소속도에 영향을 미치는 인자들로는 복사(radiation), 연소기 내부 벽에 의한 영향(chamber confinement), 점화 에너지(ignition energy)에 대한 영향, 화염의 불안정성(flame instability)이나 부력(buoyancy) 등이 있으며, 이러한 인자들의 영향을 줄이기 위해 많은 연구들이 진행되어 왔다[7], [9], [10], [11], [12], [13]. Yu 등은 수치해석으로 화염이 전파할 때 발생하는 복사 영향에 대해 연구를 진행하였는데, 복사는 화염의 연소속도를 감소시키지만 다른 인자들에 비하여 상대적으로 영향이 매우 작다고 보고하였다[11]. Zhou 등은 점화 에너지가 층류연소속도에 미치는 영향을 확인하였으며[12], Burke 등은 원통형 연소기에서 내부 벽에 의해 영향을 받은 층류연소속도를 연구하였다[13]. Cai 등은 앞서 언급한 층류연소속도 측정에 영향을 미치는 인자들의 영향을 최소화할 수 있도록 적절한 화염반경 구간을 선정하는 것을 제안하였으며[7], Chen은 메탄-공기 혼합물의 NPT(Normal Pressure and Temperature, P=0.1MPa, T=298K) 조건에서 측정된 층류연소속도와 타 연구의 결과를 비교하는 것으로 신규 연소기의 검증이 필요하다고 보고하였다[10].
이에 본 연구에서는 정확한 SNG 연료의 층류연소속도 측정을 위해 먼저 메탄-공기 혼합기를 구형으로 전파하는 화염을 이용하여 연소기 검증을 진행하였다. 아울러 선형/비선형 모델(linear and nonlinear model) 중 적합한 모델을 선정하고, 층류연소속도를 ANSIS CHEMKIN PRO의 Premix code[14]를 이용한 수치해석 결과와 비교하여 가장 낮은 오차율을 가지는 메커니즘을 채택하였으며, 이를 기반으로 SNG연료의 층류연소속도와 마크스타인길이를 다양한 압력조건에서 측정하였다.
2. 실험장치 및 측정방법
2.1. 실험장치
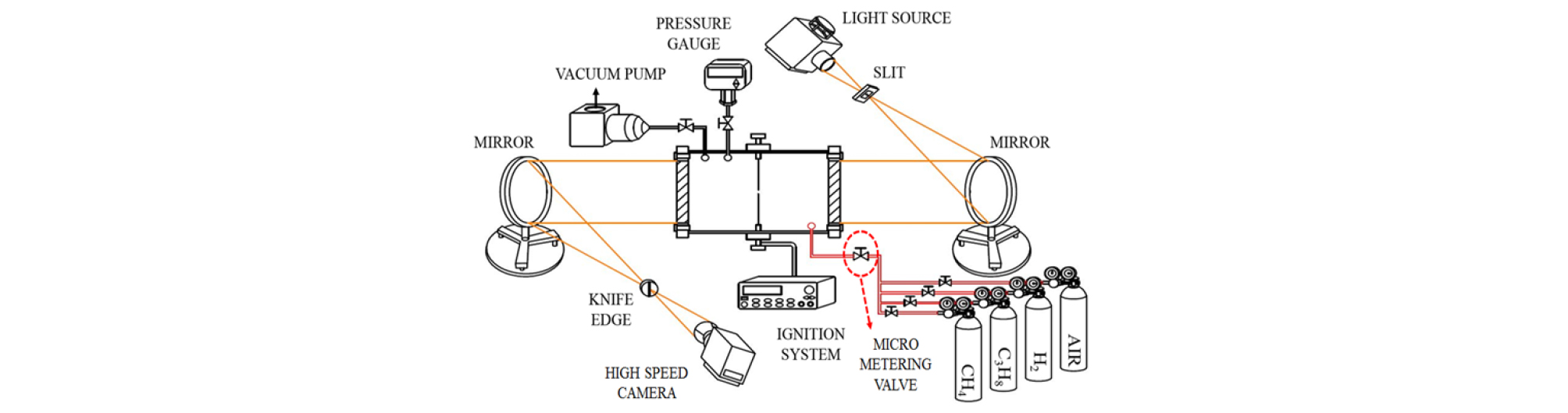
Fig. 1은 본 연구에 사용된 정적연소기와 슐리렌 장치를 나타낸 개략도이다. 연소기는 내부 직경 200 mm, 길이 220 mm의 원통형으로 양쪽에 직경 150 mm, 두께 40 mm의 석영(quartz)창을 설치하여 광학적인 접근이 가능토록 설계하였다. 혼합기의 점화를 위해 연소기 중앙에 두 개의 전극봉이 설치되어있다. 또한 연소기 내부의 압력을 측정하기 위한 전자압력계(digital pressure gauge, LabDMM), 연료유입 전 연소기 내부를 진공상태로 만들기 위한 진공펌프(vacumm pump), 마지막으로 연료유입의 정밀성을 높이기 위해 미세조절밸브(micro metering valve)를 사용하였다.
슐리렌 장치는 100 W 할로겐 광원(light source) 램프, 2개의 광학(optical)거울, 그리고 슬릿(slit)과 나이프에지(knife edge)로 구성되어 있어 측정 영역에서 화염의 밀도구배에 따른 굴절률을 나타낸다. 슐리렌 이미지는 고속카메라(Photron Inc., Fastcam 1024 pci, 384x368 pixel)를 이용하여 초당 6000 장의 이미지를 취득 후 분석하였다.
실험에 사용된 연료는 화염의 특성을 엄밀하게 관찰 가능한 고순도 연료들로 제조된 모사 SNG으로, 기존의 LNG와의 호환성을 위해 프로판과 수소로 발열량을 맞추었다. 연료 조성비 등 주요 실험조건들은 Table 1에 정리하였다.
Table 1. Experimental conditions
| Description | Specification |
| Fuel | CH4 (99.999%) C3H8 (99.5%) H2 (99.999%) |
| Composition of SNG (%) | CH4:C3H8:H2=91:6:3 |
| Oxidizer | Air (99.999%) |
| Equivalence Ratio (Ф) | 0.7 - 1.3 |
| Pressure (MPa) | 0.1, 0.3 and 0.5 |
2.2. 실험 및 측정방법
구형 전파화염을 이용한 층류연소속도 측정은 먼저 진공펌프를 이용하여 연소기 내부를 진공상태로 만든 후, 연료와 공기를 각 실험조건에 따라 몰분율(mole fraction)에 상응하는 부분압력(partial pressure)으로 조정하여 공급한다. 공급된 혼합기는 안정된 상태(well steady reactor)가 될 수 있도록 10분의 대기시간 후 점화 장치(ignition system)에 의해 두 전극봉 사이에서 스파크 발생으로 점화가 시작된다. 점화로 생성된 초기 구형화염은 중앙에서 미연혼합기 방향으로 전파되어 연소실 벽에 닿아 소화하게 되었는데, 이때 구형으로 퍼져나가는 화염의 이미지를 슐리렌 장치와 고속카메라를 이용하여 이미지를 취득한 후 MATLAB 코드를 적용하여 시간당 화염반경의 연소속도를 구하게 된다. 연소 후 연소기 내부의 배기가스는 실험실 배기 시스템을 통하여 외부로 빠져나가게 되며, 압축공기를 사용하여 연소기 내부에 응축된 수증기를 제거한다. 이 경우 실험에서 발생할 수 있는 불확실성을 줄이기 위해 동일한 조건에서 3번 이상 반복하여 실험을 수행하였다.
구형 전파화염에서 스트레치를 받는 기연가스의 연소속도(stretched burning velocity, 이하 Sb)는 dRf/dt로 정의된다. 이때 화염은 전파될수록 스트레치의 영향을 받게 되는데 스트레치율(stretch rate, 이하 K)은 K=(2/Rf)Sb로 나타낼 수 있다. 언급된 수식들에서 Rf는 화염반경(flame radius)을 의미한다. 이미지 분석과 앞의 계산식을 통해 Sb와 K가 도출되며, Sb와 K는 다음과 같은 선형관계를 갖는다[15].
| $$\mathrm{LM}\;:\;S_b=S_b^0-L_bK$$ | (1) |
식 (1)을 선형모델(Linear Model, 이하 LM)이라 하는데, 여기서 는 기연가스의 스트레치를 받지 않는 연소속도(unstretched burning velocity, 이하 ), Lb는 기연가스의 마크스타인 길이(Markstein length at burned mixture, 이하 Lb)로 식 (1)과 같이 K에 대한 Sb의 관계를 나타낸다. 이때 는 Sb−K의 그래프에서 외삽(extrapolation)을 통해 스트레치를 받지 않는 K=0인 지점에서의 연소속도 즉 을 계산할 수 있으며, 이 경우 Lb는 Sb−K 그래프에서 음의 기울기를 의미한다.
또한 LM 외에도 다음과 같이 식 (2)과 식 (3)같은 비선형모델을 사용하여 을 계산할 수 있다.
| $$\mathrm{NM}\;\mathrm I\;:\;S_b=S_b^0-S_b^0L_b\;\cdot\;(2/R_f)$$ | (2) |
식 (2)은 충분히 큰 Rf를 가정하여 Frankel과 Sivashinsky에 의해 제안된 비선형모델(Non linear Model Ⅰ, 이하 NMⅠ)로 화염곡률(flame curvature) 2/Rf과 Sb의 그래프에서 외삽을 통해 와 Lb을 계산할 수 있는 모델이다[16].
| $$\mathrm{NM}\;\mathrm{II}\;:\;\ln(S_b)=\ln(S_b^0)-S_b^0L_b\;\cdot\;2/(R_fS_b)$$ | (3) |
식 (3)은 Kelley와 Law에 의해 제안된 비선형 모델(Non linear Model Ⅱ, 이하 NM Ⅱ)로 ln(Sb) - 2/(RfSb) 그래프에서 외삽을 통해 와 Lb를 구할 수 있는 비선형 모델이다[17].
위의 3가지 이론모델에서 공통적으로 를 구할 수 있으며, 최종적으로 구형 전파화염의 층류연소속도, 즉 미연가스의 스트레치를 받지 않는 연소속도(unstretched laminar burning velocity at unburned mixture, 이하 )는 질량보존관계식인 을 통해 계산된다. 여기서 ρb와 ρu는 기연가스와 미연가스의 밀도를 의미하며, 평형상태로 가정하여 EQUIL code를 이용하여 계산하였다[14].
그러나 위의 3가지 식에 의해 계산되는 와 Lb는 전파해 나가는 구형화염의 반경 범위에 의존적이다. 따라서 연소속도 측정과정에서 적절한 Rf의 범위를 설정하는 것은 매우 중요하다. 이를 위해 먼저 두 전극봉 사이 스파크에 의해 화염의 핵(flame kernel)이 생성된 직후 연소속도가 점화에너지에 의해 영향을 받지 않도록 충분히 큰 최소 화염반경(lower flame radius, 이하 RfL)을 설정해야 한다. 또한 최대 화염반경(upper flame radius, 이하 RfU)은 화염의 불안정성(flame instability), 복사(radiation) 그리고 연소기 내부 벽(confinement)의 영향이 배제될 수 있도록 충분히 작은 값을 선정해야 한다[7], [9], [10].
한편, 높은 정확도의 를 얻기 위해 많은 연구자들에 의해 Rf의 범위 선정과 연소속도측정에 영향을 미치는 인자들에 대한 연구가 진행되어왔다. Bradley 등은 RfL이 6 mm 이상일 경우 점화에 의한 영향이 배제될 수 있다고 보고하였으며[18], Kelly 등은 Sb−K 그래프에서 점화에너지 변화에 따른 연소속도의 변화를 분석함으로써, 초기 점화단계에서의 점화에너지(ignition energy)에 대한 영향을 분석하였다[17]. Chen등은 RfU가 40 mm 이하일 경우 복사에 의한 영향을 무시할 수 있다 하였으며[20], RfU/RW가 25% 미만일 경우 연소기 내부 벽의 영향을 최소화할 수 있다고 보고하고 있다[13]. 원형이 아닌 연소기의 경우 RW=(3V/4π)1/3로 구할 수 있으며, 여기서 RW 와 V는 각각 연소기 내부 반경과 연소기의 체적을 의미한다. 이에 본 연구에서는 정적연소기에서 화염 반경선정에 관한 이들의 연구결과를 참조하여 연구에 반영하였다.
또한, 물질-열확산 불안정성(diffusional-thermal instability), 수력학적 불안정성(hydrodynamic instability) 그리고 부력(buoyancy)에 의해 층류연소속도가 영향을 받을 수 있다. 이중 물질-열확산 불안정성의 경우 단일 Le 수(Lewis number)보다 작은 조건(Le<1)에서 발생하는 것으로 알려져 있는데, NPT 조건의 메탄-공기 혼합기는 단일 Le 수에 근접한 값(Le≈1)을 가지고 있기 때문에[10], [20] 메탄이 주성분인 SNG연료에서는 해당 불안정성을 배제할 수 있었다. 수력학적 불안정성도 구형화염이 성장함에 따라 열팽창률(thermal expansion ratio)과 화염의 두께에 영향을 받아 발생하므로 충분히 작은 RfU를 선정함으로써, 수력학적 불안정성에 의한 영향을 배제할 수 있었다[7]. 추가적으로 부력의 영향을 극복할 수 있도록 충분히 높은 층류연소속도를 가지는 당량비 0.7에서 1.3까지 0.1씩 증가시켜 층류연소속도가 15 cm/s 이상이 될 수 있도록 실험조건을 설정하였다[21].
마지막으로 본 연소기에 가장 적합한 이론모델과 반응메커니즘을 선정하기 위하여 LM, NM I, II로 도출된 실험값과 ARAMCO 2.0[22], GRI 3.0[23], USC-II[24] 그리고 UC San Diego[25] 반응메커니즘으로 계산된 값을 비교하였고, 이중 가장 낮은 오차율을 가지는 모델과 반응메커니즘을 선정하였다. 이로써 SNG 연료에 적합한 정적연소기는 메탄이 91%인 관계로 먼저 메탄-공기 혼합기를 통해 검증한 후 이를 바탕으로 SNG 연료의 와 Lb를 초기압력 조건인 0.1 MPa에서 0.5 MPa 까지 상승시켜 측정하였다.
3. 실험결과 및 검토
3.1. 이론모델 및 반응메커니즘의 검증
최적화된 반응메커니즘이 알려져 있지 않은 SNG 연료의 실험검증을 위해 SNG 연료에 91%를 차지하는 메탄-공기 혼합기를 사용하여 연소기를 검증하였다.
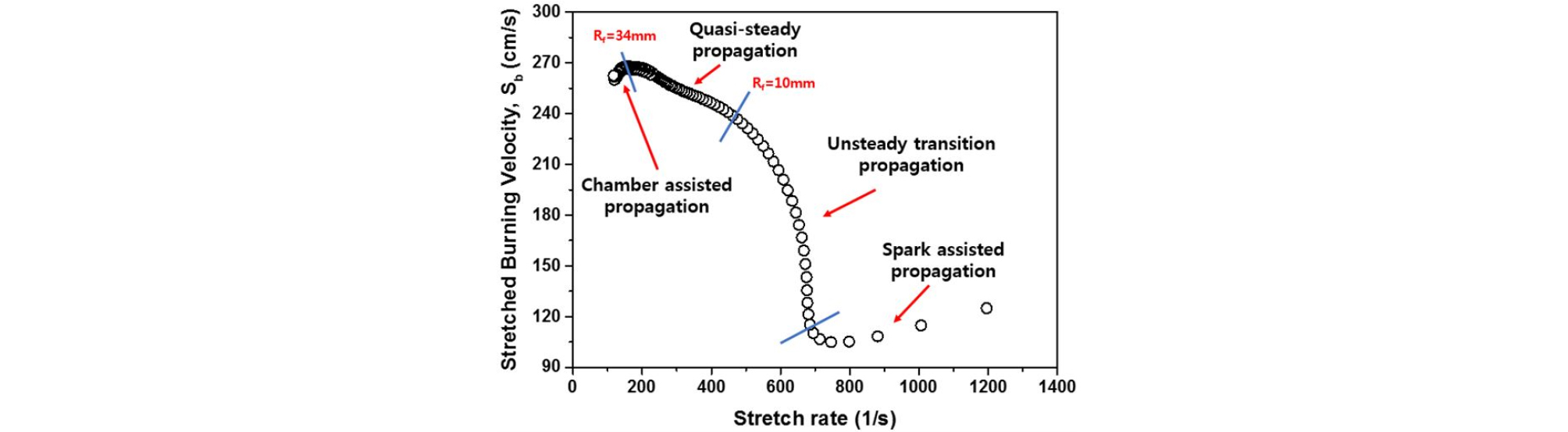
먼저 적합한 Rf의 범위를 설정하기 위해 NPT 조건에서 K의 변화에 대한 Sb의 거동을 Fig. 2에 나타내었다. 초기 화염전파 구간에서는 점화에너지에 의한 영향으로 Sb가 점차 감소하는 전파구간(spark assisted propagation)이 발생하였고, 비선형적으로 Sb가 상승하는 천이구간 (unsteady transition propagation)이 나타났다. 이후 그래프의 기울기가 감소하며 Sb가 선형적으로 증가하는 전파구간(quasi- steady propagation)이 확인되었다. 이러한 경향은 모든 화염에서 공통적으로 나타나는 현상으로 확인되었다. 또한 화염이 연소실 벽면에 도달하였을 때(chamber assisted propagation)에는 Sb가 급격하게 줄어들며 소화하게 된다.
Fig. 2에서 볼 수 있듯이 Rf>10 mm에서는 점화 에너지로부터 Sb의 변화가 안정되는 것을 확인하였으며, 연소기 벽에 의한 영향을 피하기 위해 최대 화염의 반경은 Burke 등[13]이 보고한 RfU/RW < 25%가 되는 29.54 mm 로 계산되었다. 층류연소속도 측정에 사용된 화염의 반경이 클수록 낮은 오차율을 가지기 때문에[6] 최종적으로 연구에 사용된 Rf의 범위는 10<Rf<29 mm로 설정하였다.
설정한 Rf 범위(10-29 mm)를 이용하여 메탄-공기 혼합물의 층류연소속도를 각 모델별로 도출하였으며, 그 결과를 4가지 반응메커니즘으로 계산된 수치해석 결과와 비교하였다.
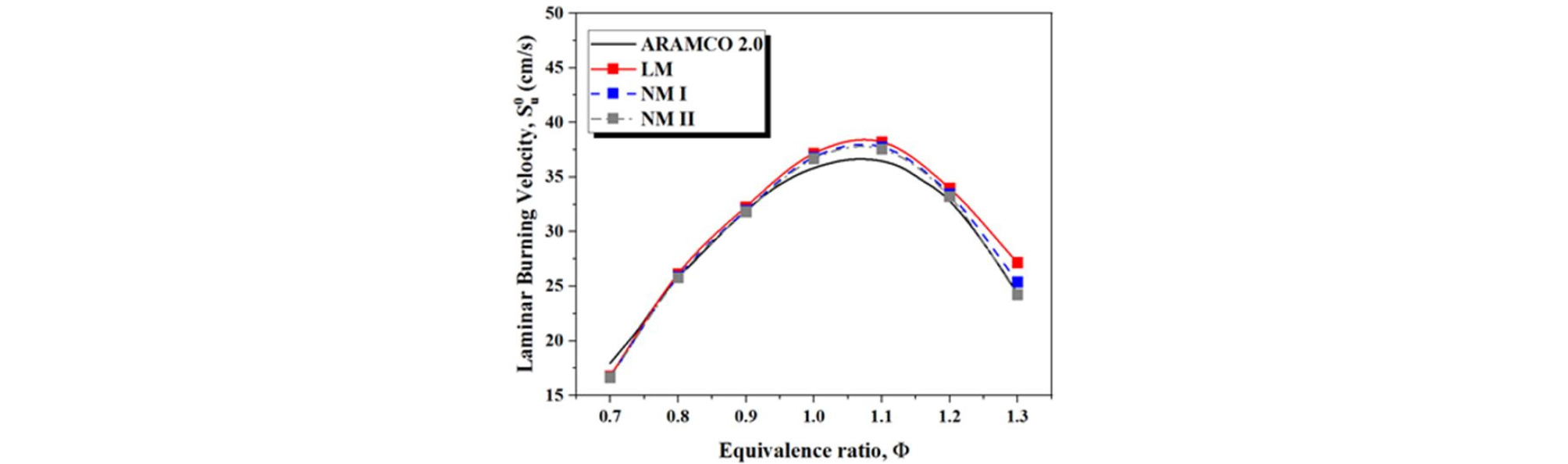
Fig. 3은 세 가지 이론 모델로 측정된 실험값과 ARAMCO 2.0으로 예측된 값을 비교한 그래프이다. 세 가지 모델은 당량비 1.3 구간을 제외하고 근사한 결과값을 보였으며 이중 LM이 가장 큰 값을 가졌다. 이러한 방식으로 반응메커니즘의 계산 값과 실험값을 비교하여 각 오차율을 Table 2에 나타내었다. LM과 NM I의 경우 USC-II 메커니즘이 3.2와 2.5%의 가장 낮은 오차율을 가졌지만, NM II의 경우 ARAMCO 2.0 메커니즘이 2.2%로 전체에서 가장 낮은 오차율을 나타내었다. 이를 통해 결과적으로 NM II와 ARAMCO 2.0 메커니즘을 SNG 연료의 와 lb를 측정하기 위한 모델로 선정하였다.
Table 2. Average error rates in experimental laminar burning velocity of CH4-Air mixture against calculation at NPT condition
| Mechanisms | Error rate (%) | ||
| LM | NMⅠ | NMⅡ | |
| GRI 3.0 | 4.7 | 3.6 | 3.1 |
| USC-II | 3.2 | 2.5 | 3.3 |
| UC San Diego | 10.1 | 8.6 | 7.8 |
| ARAMCO 2.0 | 4.4 | 2.9 | 2.2 |
3.2. SNG 연료의 와 lb
정적연소기를 이용하여 압력별 구형 전파화염의 와 Lb를 측정하였고 이를 수치해석 결과와 비교하였다.
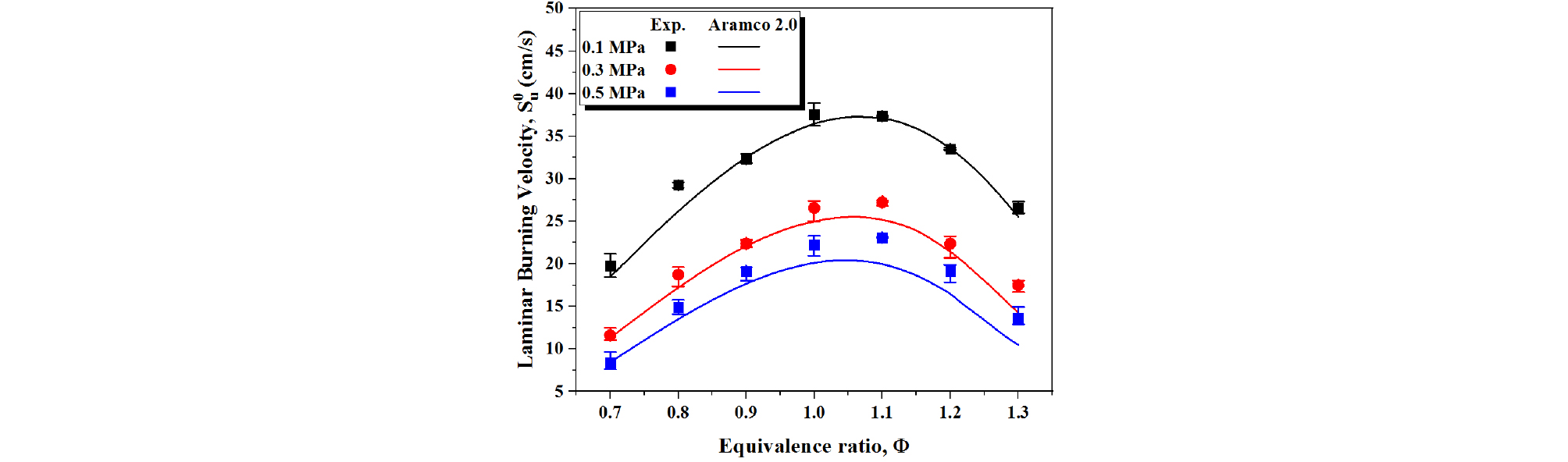
Fig. 4는 연소기 검증으로 선정된 NM II로 구한 SNG 연료의 를 압력과 당량비 변화에 따라 나타내었으며, 이를 앞 절에서 적절한 반응메커니즘으로 선정한 ARAMCO 2.0으로 계산된 수치해석 결과와 비교한 그래프이다. 당량비에 따른 의 증감은 메탄-공기 혼합기와 동일한 경향을 보이며, 의 최댓값 구간은 당량비 1.0에서 1.1으로 유사하다. 반면에 메탄-공기 혼합기의 수치해석 결과보다 대략 0.5 cm/s가량 더 높은 값을 가지는 것으로 나타났다. 초기압력이 증가함에 따라 가 감소하는데, 이는 압력이 상승함에 따라 내부 미연가스의 밀도가 증가하였고, 또한 동일한 당량비 조건에서 체인 분기반응(branching reaction)이 일정한 반면 체인종결반응(inhibiting reaction)이 강화되기 때문이다[8].
한편, 실험으로 측정할 수 없었던 높은 압력과 온도 조건에서의 층류연소속도는 Power law 관계식 (4)를 이용하여 예측할 수 있다[26]. 본래의 수식에는 온도 변화에 대한 항이 포함되어 있지만, 본 연구에서는 초기온도 조건을 298 K로 고정시켜 온도에 대한 항은 배제하였다.
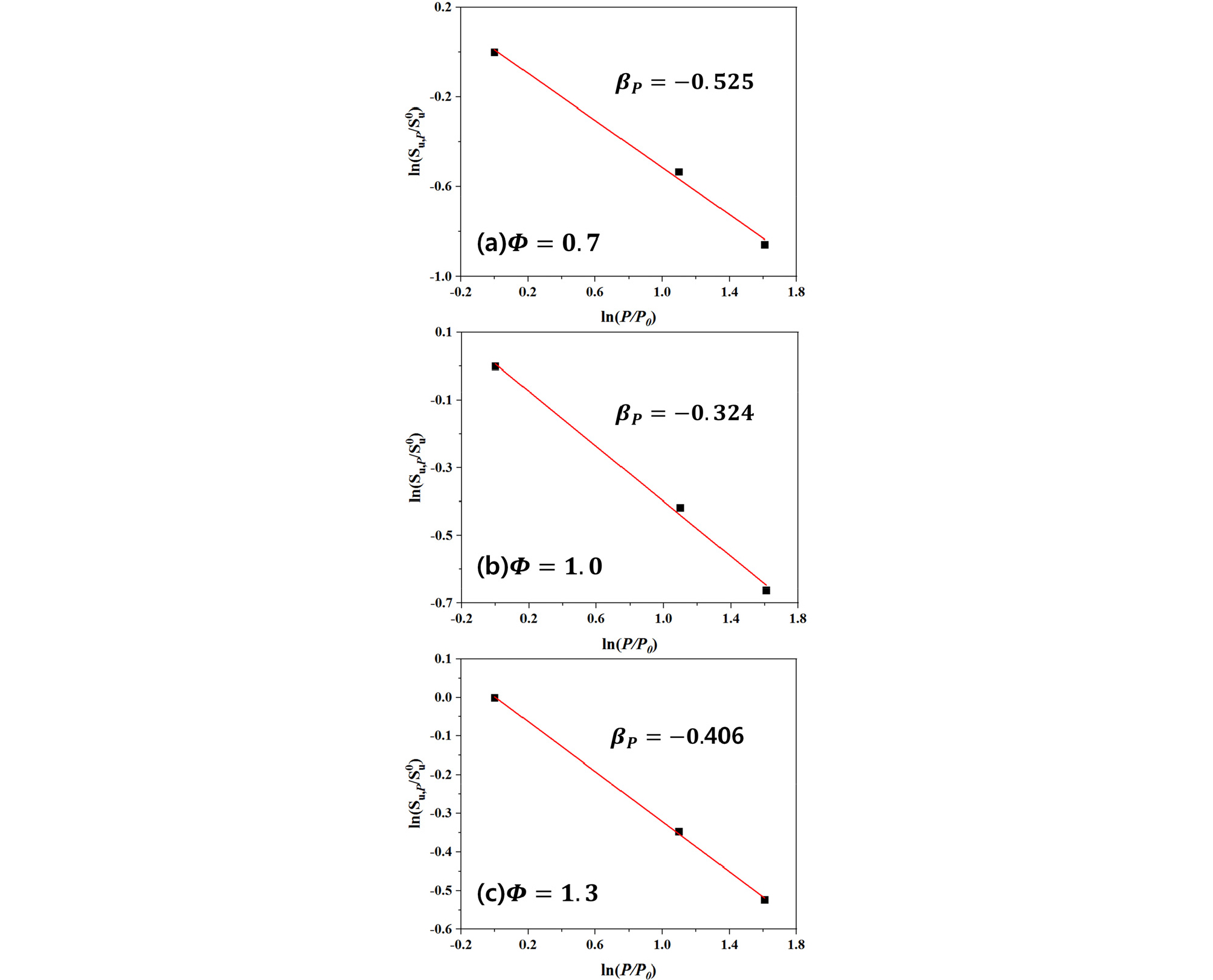
| $$S_{u,P}=S_u^0{(\frac P{P_0})}^{\beta_p}$$ | (4) |
여기서 P0는 기준조건의 압력, 즉 0.1 MPa이며, 는 기준조건에서의 층류연소속도, Su,P는 압력 P에서의 층류연소속도이다. βP는 압력 지수(pressure exponent)로, ln(Su,P/)와 ln(P/P0)의 그래프에서 기울기를 통해 구할 수 있다. Fig. 5는 당량비 0.7, 1.0, 1.3 조건에서의 βP을 나타낸 그래프이다. 당량비 0.7 조건에서 βP값은 -0.525로 확인되었으며 당량비가 증가함에 따라 그 값이 증가하여 당량비 1.0 조건에서 βP값이 -0.324로 측정되었다. 그러나 당량비 1.3조건 에서는 βP값은 -0.406으로 다시 감소하여 이전 연구자들에 의해 구해진 메탄-공기 혼합기의 βP값과 유사한 것으로 확인되었다[27].
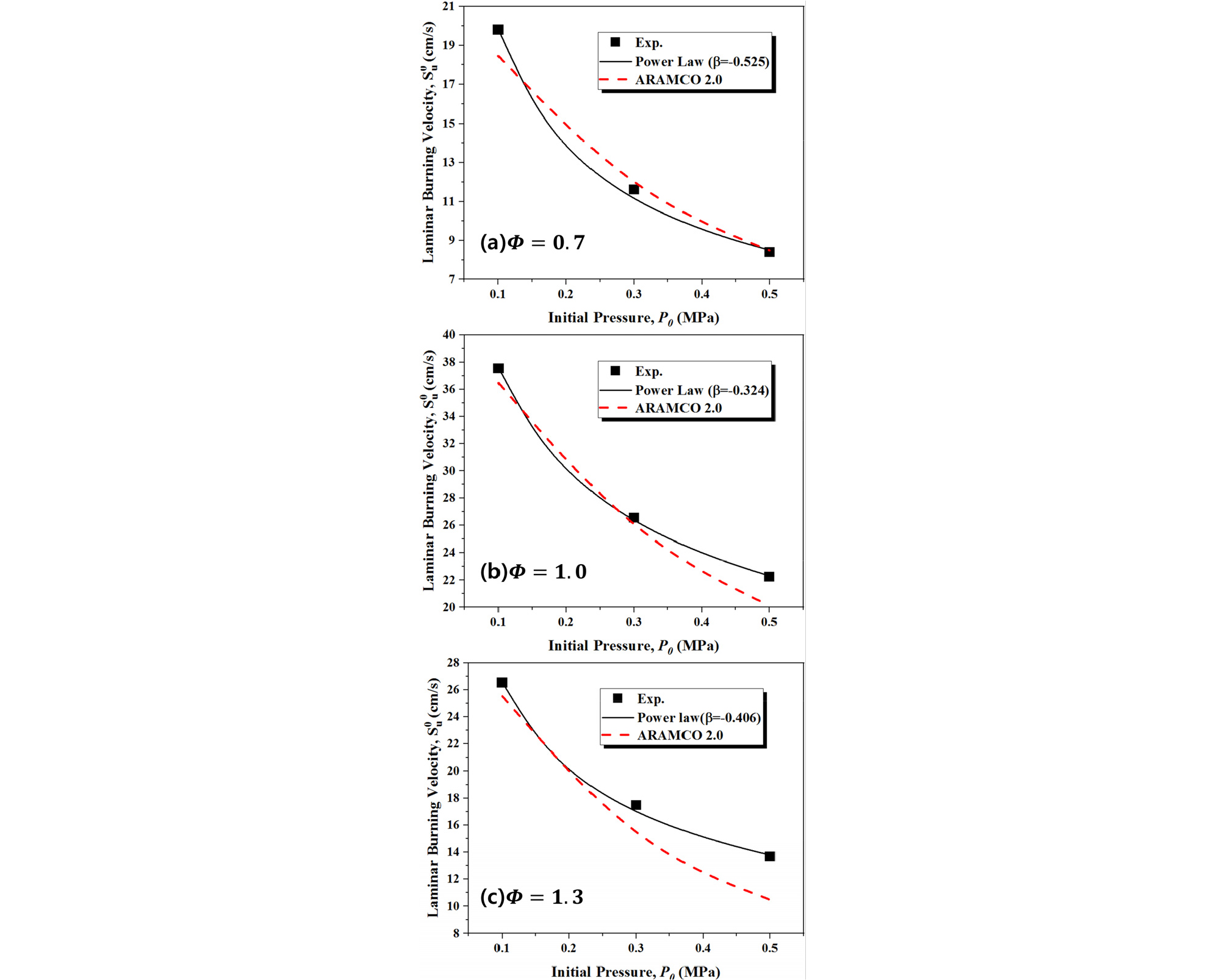
Fig. 6은 압력에 따라 앞서 얻어진 βP값을 식 (4)에 대입하여 예측한 값과 ARAMCO 2.0으로 계산된 수치해석 결과를 비교한 그래프이다. 그래프에서 보는 바와 같이 당량비 0.7 조건에서는 압력이 증가하더라도 예측 값과 수치해석 결과가 잘 일치하였다. 당량비 1.0 조건에서도 낮은 압력에서는 두 값이 비교적 일치하였으나, 압력 0.5 MPa에서 약간의 차이를 보였다. 마찬가지로 당량비 1.3 에서도 압력이 증가할수록 예측값과 수치해석 결과의 차이가 발생하였는데, 이때의 격차는 당량비 1.0 조건보다 약 2배 정도 크게 나타났다. 이는 더 높은 초기압력 조건에서의 실험값과 비교를 통한 반응메커니즘 수정을 통해 오차율을 향상시킬 수 있을 것으로 사료되며 향후 추가적인 연구로 보고할 예정이다.
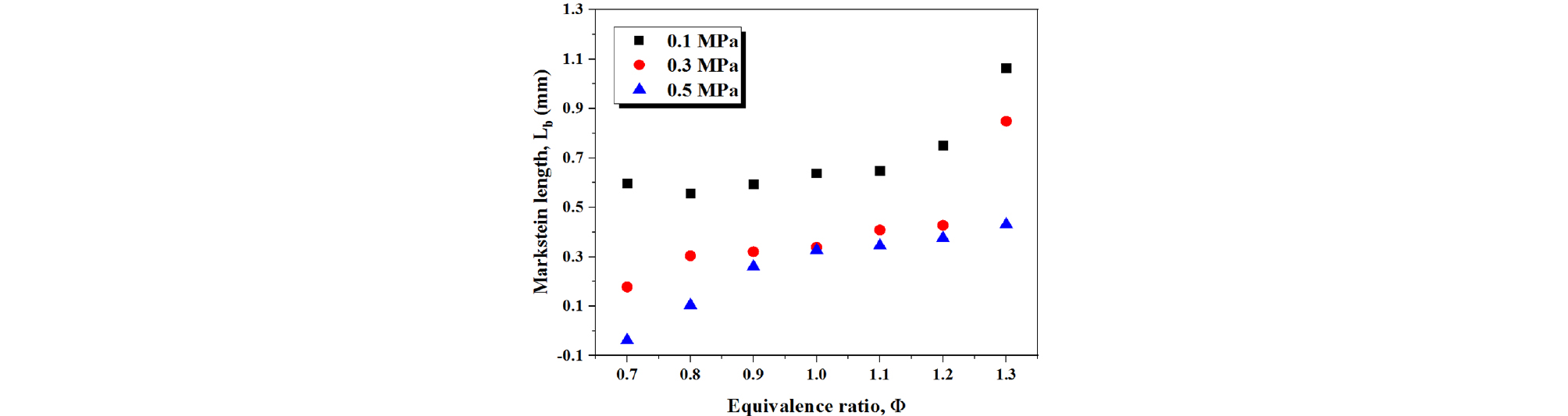
가연성 혼합물의 중요한 인자중 하나인 Lb를 당량비와 초기압력 조건을 변화시켜 측정하였으며 그 결과를 Fig. 7에 나타내었다.
대부분의 조건에서 측정된 Lb는 양수 값을 보였는데, 이는 화염면의 불안정성이 억제되는 것을 의미한다[28]. 당량비가 증가함에 따라 Lb 값이 증가하였으며, 압력이 증가함에 따라 Lb가 감소하는 것이 확인되었다. 이는 압력이 증가함에 따라 비선형적인 K의 거동과 점화에너지에 의한 영향력 등이 줄어들고[5]Lb가 감소하여 화염의 안정성이 감소하는 것을 의미한다[28]. 일반적으로 압력 증가에 따른 셀 불안정성은 연소속도에 영향을 미쳐 정확한 측정에 방해가 되는데, 여기에서는 미약하여 구형화염의 이미지를 추가하지 않았지만, 본 연구에서 측정된 SNG 화염의 표면 셀 형상은 연소속도에 영향을 주지 않았으며 일부 셀은 전극봉에 의해 발생된 것으로 판단되었다.
4. 결 론
구형으로 전파하는 화염으로부터 SNG 연료의 층류연소속도를 측정하기 위해 메탄-공기 혼합기를 사용하여 연소기 검증을 실시하였다. 이를 토대로 SNG 연료의 와 Lb를 측정하였으며 다음과 같은 결론을 도출하였다.
1) 연소기 타당성을 검증하기 위해 메탄-공기 혼합기의 NPT 조건에서 3가지 이론모델을 이용하여 혼합기의 를 측정하였으며, 메탄 반응 묘사에 최적화된 수치해석 결과와 비교하였다.
2) 수치해석 결과와의 비교를 통해 가장 낮은 평균 오차율(2.2%)을 보인 NMⅡ와 ARAMCO 2.0 메커니즘을 사용하여 를 측정하였고, 이 경우를 해당 연소기에서 SNG 연료의 측정을 위해 가장 최적화된 조건으로 선정하였다.
3) SNG 연료는 당량비에 따른 의 경향이 메탄-공기 혼합기와 일치하는 것을 확인할 수 있었다. 또한 초기압력이 증가함에 SNG 연료의 가 감소하는데, 이는 연소기 내부 미연가스의 밀도가 증가하는 것과, 체인 분기반응이 일정한 반면 체인 종결반응이 강화된 것으로 판단하였다.
4) Power law 관계식을 이용하여 층류연소속도를 예측하였으며 βP값이 당량비 0.7, 1.0, 1.3에서 각각 –0.525, -0.324, -0.406으로 측정되었다. 또한 ARAMCO 2.0 메커니즘으로 계산된 수치해석 결과와 비교하였으며 상대적으로 낮은 압력조건에서 수치해석 결과와 실험값이 잘 일치하는 것을 확인할 수 있었다. 하지만 압력과 당량비가 증가할수록 그 차이가 커지는 것을 확인하였다.
5) 대부분의 조건에서 양수 값의 Lb가 측정되었으며. 초기압력이 증가함에 따라 Lb가 감소하는 경향이 확인되었다. 이는 압력이 증가함에 따라 화염이 불안정해지며, 비선형적인 K의 거동, 점화, 그리고 선택되는 Rf의 영향이 줄어드는 것을 의미하였다.
기호설명
Sb : Propagation burning velocity at burned mixture(cm/s)
: Unstretched laminar burning velocitat burned mixture(cm/s)
: Unstretched laminar burning velocityat unburned mixture(cm/s)
Lb : Markstein length at burned mixture(mm)
K : Stretch rate(1/s)
Rf : Flame radius(mm)
RfL : Lower flame radius(mm)
RfU : Upper flame radius(mm)
RW : Inner radius of chamber(mm)
ρb : Density of burned mixture(g/cm3)
ρu : Density of unburned mixture(g/cm3)