1. 서 론

전 세계적으로 깨끗한 환경에 대한 관심이 높아지고 특히 대기환경문제가 대두되면서 화석연료의 사용으로 배출되는 배기가스에 대한 규제들이 더욱 엄격해지고 있다. 대표적인 온실가스인 이산화탄소(CO₂)는 화석연료의 연소과정에서 필수적으로 발생하게 되고 일산화탄소(CO), 질소산화물(NOx), 탄화수소(HC), 황산화물(SOx) 등의 공해물질 배출로 인하여 미세먼지 등 대기오염 및 지구 온난화와 같은 문제가 심각한 실정이다. 따라서 이러한 문제점을 해결하기 위하여 화석연료의 연소과정에서 발생되는 공해물질을 저감하는 친환경연소 및 에너지효율의 증가를 위한 많은 연구들이 진행되고 있다[1], [2], [3], [4].

이 중에서도 연소과정에서 발생된 기연가스의 강한 재순환을 통하여 산화제 및 연료를 희석시켜 낮은 산소농도조건에서 연소하는 MILD(Moderate or Intense Low- oxygen Dilution) 연소기술에 대한 관심이 높아지고 있다[5], [6], [7]. 이러한 MILD 연소기술은 빠른 유동의 속도에 비하여 낮은 산소농도로 인한 화학반응속도가 상대적으로 감소되어 기존의 국부적인 연소화염의 형태가 감소되고 1,500°C이하의 낮은 화염온도와 체적연소를 형성하여 Thermal NOx의 배출을 근원적으로 방지할 수 있다는 장점을 가지고 있다[8], [9], [10], [11].

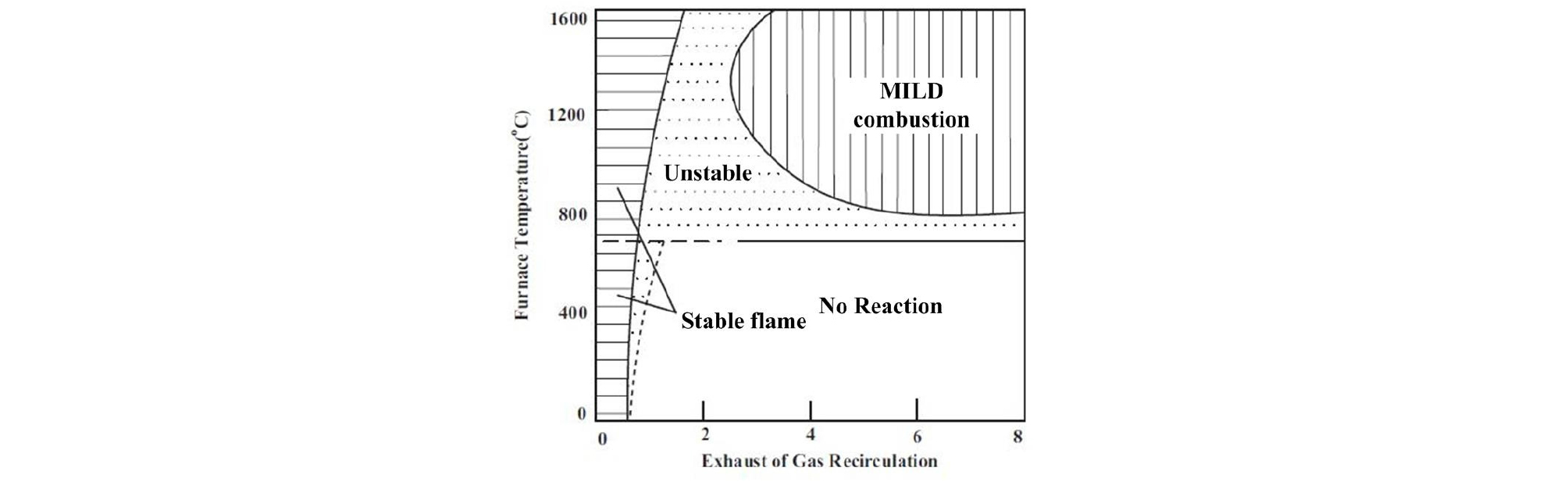
따라서 배기가스의 재순환은 MILD연소에서 매우 중요한 역할을 하는데 이에 Wünning [12], [13] 등은 배기가스 재순환율($K_V$)과 연소로 내부 온도로 나타내어지는 MILD연소의 형성영역을 Fig. 1과 같이 제시하였으며 이때의 배기가스 재순환율($K_V$)는 식 (1)과 같이 정의 하였다.

여기서 $\dot{m_r}$, $\dot{m_f}$와 $\dot{m_a}$은 각각 재순환된 기체, 초기 공급 연료 및 공기의 질량유량을 나타내며, 배기가스 재순환율 $K_V$는 재순환하는 가스의 질량유량을 공급되는 연료와 산화제의 질량유량으로 나눈 값으로 정의 하였다. MILD연소의 안정성 영역을 나타낸 Fig. 1을 살펴보면 재순환율이 3이상 노 내부의 온도가 연료의 자발점화온도 이상인 800°C이상의 조건에서 MILD연소를 형성함을 나타내었다.

Fig. 1.

Schematics of MILD combustion stability limits[12].

이러한 MILD연소기술에 신재생에너지인 바이오매스를 연료로 적용하고자하며 바이오매스 중에서도 에너지밀도가 높고 보관 및 저장, 생산 등에서 많은 장점을 가지고 있는 바이오 연료인 바이오에탄올을 사용한다면 온실가스배출규제 및 온실가스목표관리제 등 강화되는 배기가스 저감측면에서 큰 이점을 가져올 수 있다. 바이오에탄올은 사탕수수, 밀, 옥수수 등과 같은 녹말이 함유된 곡물들의 당을 추출하여 생성하는데 바이오에탄올의 발효 및 연소과정에서 발생되는 이산화탄소를 식물체가 광합성을 통하여 흡수한 이산화탄소로 감각하여 Table 1과 같은 과정에 의하여 이산화탄소 발생량이 “0”인 탄소 중립(Carbon Neutral) 연료로 인정받는 신재생에너지의 하나이다. 따라서 바이오에탄올을 연료로 사용한 연소시스템의 경우 현행 배기규제에서 이산화탄소 배출에 대한 규제를 받지 않게 되고 NOx배출에 대한 규제만이 중요해진다.

액체연료를 사용한 MILD연소기술을 적용하기 위해서는 기존의 MILD연소형성을 위한 중요인자이외에도 액체연료의 분무와 증발과 같은 물리적인 문제들을 추가로 고려해야 한다. 본 연구에서는 이러한 문제를 해결하기 위하여 Fig. 2와 같이 하단에 예혼합 연소기를 적용하여 예혼합 연소 후 발생되는 고온의 연소가스를 통하여 상단의 주 반응구간에 분사되는 에탄올연료를 연소시키는 2단 연소시스템을 구성하였다. 특히 공급되는 고온희석가스의 유속과 산소농도를 변경하며 에탄올연료의 MILD연소형성에 미치는 영향을 3차원 수치해석연구를 통하여 분석하였고 실험결과와 비교하였다. 이를 통하여 기연가스의 여러 물리적 인자들이 MILD 형성에 미치는 영향을 알아보고 아울러 NOx 배출저감에 기여하는 정도를 알아보고자 한다.

Fig. 2.

Direct photo of 2 stage ethanol MILD combustion system.

2. 수치해석방법

2.1 지배방정식

2단 연소방식을 적용한 에탄올 MILD연소시스템의 3차원 수치해석을 수행하기 위하여 상용전산수치해석 프로그램인 Ansys Fluent를 적용하여 수치해석을 진행하였고 다음과 같은 연속방정식, 운동량보존방정식, 에너지보존방정식, 화학종보존방정식을 적용하였다.

2.2 수치해석모델

SIMPLE 알고리즘을 바탕으로 수치해석에 사용된 난류모델은 Realizable $k-ϵ$ 모델을 적용하였고 Radiation을 고려하기 위하여 DO(Discrete Ordinates)모델을 적용하여 수치해석을 진행하였다. 본 수치해석에서 하단부의 예혼합연소기를 통한 반응은 계산하지 않고 Ansys Chemkin pro를 통하여 계산된 각 산소농도별 몰분율과 실험을 통하여 측정된 온도를 적용하여 입구경계조건에 예혼합연소 후 생성된 가스가 바로 공급된다고 가정하였다. 이에 따른 각 산소농도별 희석가스의 조성은 Table 2와 같고 각 조성과 온도에 따라 FGM(Flamelet Generated Manifold)을 사용하여 난류와 화학반응과의 상호작용을 고려하였다.

FGM은 Mixture fraction, Scalar dissipation, Progress variable과 같은 몇 가지 변수에 의해 모든 화학종과 온도를 매개변수화하고 3차원 해석과정에서 이러한 매개변수에 대한 전송 방정식을 푼다. 이러한 FGM을 활용한 난류화염의 수치해석기법은 계산에 소요되는 시간과 비용을 감축할 수 있다는 큰 장점을 가지고 있고 특히 FGM모델을 사용한 MILD연소에 대한 수치해석결과가 실제 현상을 잘 예측하고 있음을 선행연구를 통해 검증된 바 있다[14], [15], [16], [17]]. 본 연구에서 에탄올에 대한 FGM을 형성하기 위하여 사용한 화학반응메커니즘은 Lawrence Livermore National Laboratory에서 개발된 57개의 화학종과 383개의 화학반응으로 구성된 Marinov[18]에 NOx 반응을 추가하여 만든 61개 화학종과 395개 화학반응으로 구성된 메커니즘을 사용하였다.

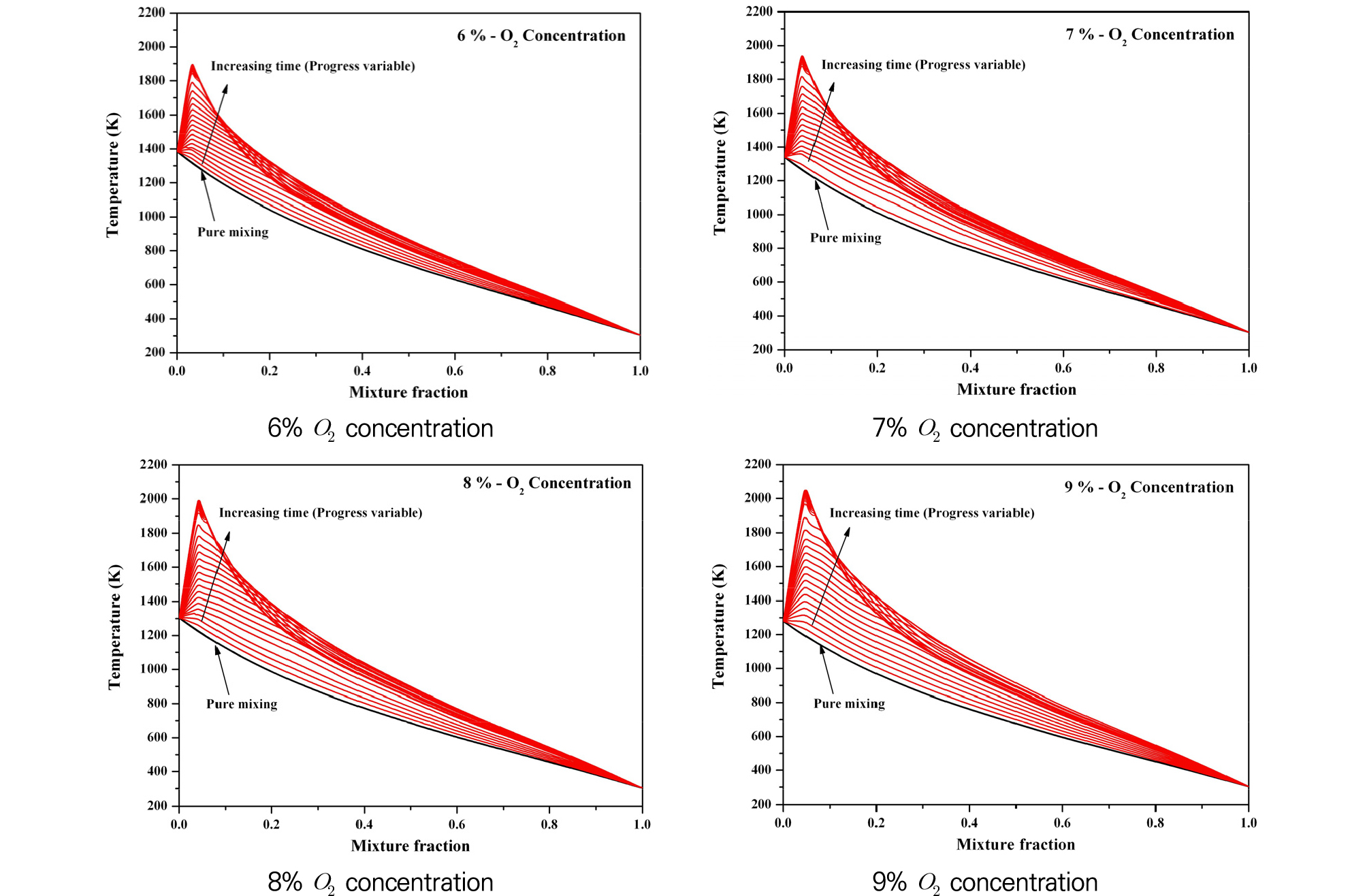
Mixture fraction에 대한 온도분포를 나타낸 Fig. 3의 FGM 생성데이터를 살펴보면 희석가스의 산소농도가 증가함에 따라 발생되는 반응온도가 약 1900 K에서 2100 K으로 증가되는 것을 확인할 수 있다. 이는 희석가스의 산소농도변화에 따라 발생할 수 있는 최고 온도가 이미 정해져있음을 알 수 있고 FGM을 이용한 수치해석과정에서 도출되는 Mixture fraction 및 Progress variable에 따라서 설정된 온도 값을 적용하게 된다.

Fig. 3.

FGM data for temperature versus mixture fraction at different oxygen concentration.

액체상의 바이오에탄올연료는 수치해석영역의 중앙에 위치한 노즐지점으로부터 Point 분사가 되는 것으로 가정하였으며 분무 유동장 해석을 위해 DPM 모델을 사용하여 입자와 대기 중 공기와의 상호교환 고려하였고 이때의 Particle trajectory의 계산은 다음 식과 같다.

여기서 $F_D$는 각 단위 입자 질량에 대한 항력이고 $F_z$는 외력이며, $u$는 유체상의 속도, $u_p$는 입자의 속도, $\mu$는 유체의 점성, $\rho$는 유체의 밀도, ${\rho }_P$는 입자의 밀도, $d_P$는 입자의 직경이며 $C_D$는 항력계수이다. $Re$는 상대레이놀즈수로 정의는 아래 식(8)과 같다.

본 연구에서 사용된 Pressure-swirl atomizer에 대해서는 LISA 모델을 사용하였다. LISA 모델은 Kelvin- Helmholtz 웨이브가 sheet에서 성장하고 결국 액체를 ligaments 형태로 부순다고 가정한다. 2차 breakup의 경우 Kelvin-Helmholtz/Rayleigh-Taylor(KHRT) 모델을 사용하였다[19].

2.3 에탄올 MILD 연소시스템 모델링

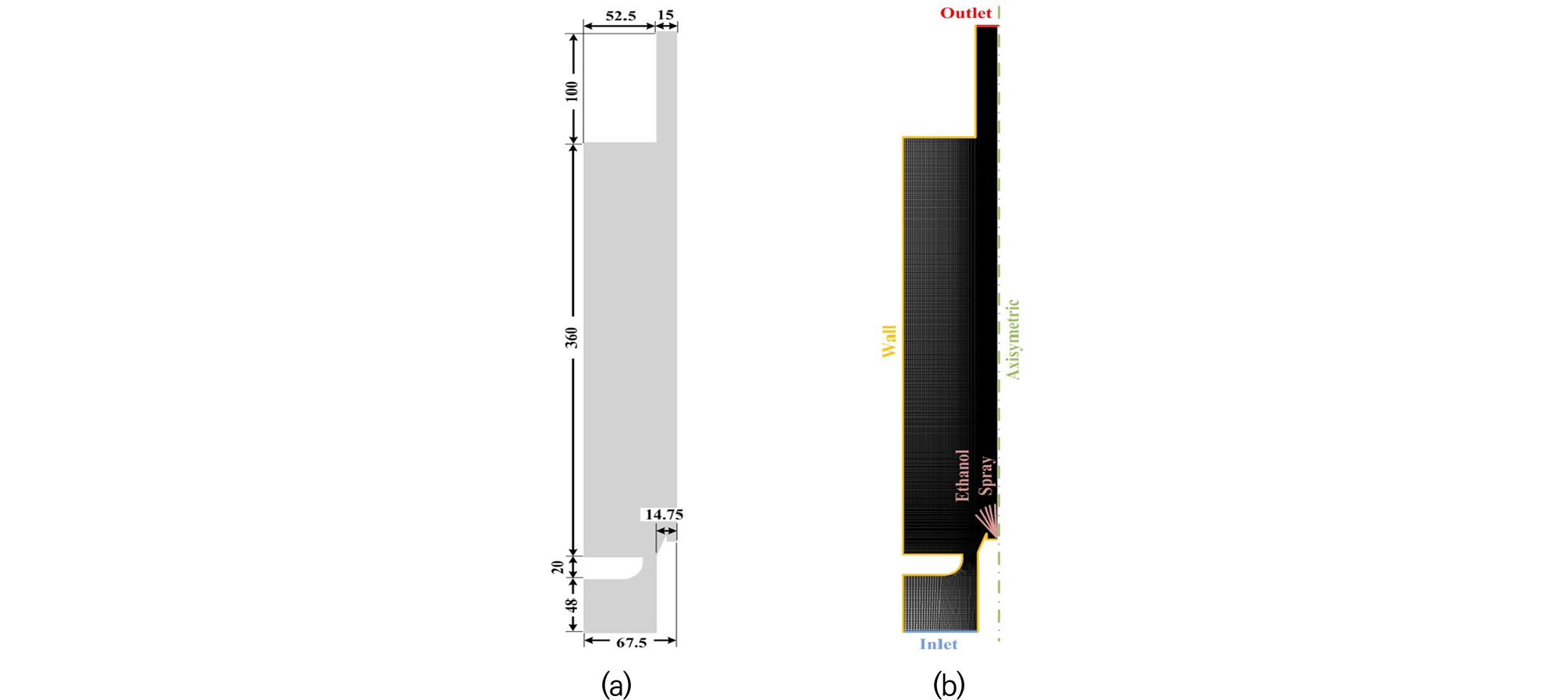
Fig. 2와 같은 2단 연소방식을 적용한 에탄올 MILD 연소시스템을 모델링하기 위해 축대칭조건을 적용하여 3차원 실린더 형상의 2단 에탄올 MILD 연소시스템을 Fig. 4와 같이 축대칭으로 모델링하였다. 모델링된 연소실을 나타낸 Fig. 4(a)를 살펴보면 반지름 67.5 mm, 길이 360 mm의 주 반응영역을 기준으로 velocity control adapter와 하단부에 48 mm길이의 예혼합연소영역이 위치하고 있다. 주 반응영역의 상부에는 반지름 15 mm에 길이 100 mm인 배기출구를 위치시켜 모델링 하였다. Fig. 4 (b)에서 나타낸 격자구조의 경우 열유동 수치해석에 수렴성 및 정밀성이 뛰어난 사각격자를 활용하였고 약 40,000개의 격자를 구성하여 수치해석에 적용하였다.

Fig. 4.

Schematic for the computational domain of (a) dimension (mm), (b) mesh structure and boundary conditions.

3. 결과 및 고찰

3.1 수치해석모델 검증

2단 연소방식을 적용한 에탄올 MILD연소시스템의 수치해석을 진행하기 위하여 가장 중요하게 고려되어야할 부분은 액체인 에탄올의 분사모델이다. 이와 같은 액체연료 분사모델의 검증을 위하여 Ansys Fluent의 Spray 모델을 사용하여 Eindhoven High Pressure Cell(EHPC)와 Sandia National Laboratories[20]의 분사실험결과를 모사하여 동일한 조건으로 계산을 수행하였고 그 비교결과를 Fig. 5에 나타내었다. 작동유체는 실험에서 사용한 Heptane연료로 하여 시간에 따른 액적의 분사거리를 측정하였고 수치해석결과와 비교해보면, EHPC의 경우 분사초기에 수치해석을 통한 연료분사 길이가 약간 길게 예측되지만 시간이 흐름에 따라 실험결과와 동일한 분사 길이를 나타내었다. 반면 Sandia의 경우 분사 초기의 분사 길이는 정확하게 예측하고 있지만 시간이 경과함에 따라 예측되는 spray의 분사 길이가 실험결과에 비해 짧게 예측되는 것을 볼 수 있다. 그러나 발생하는 오차는 3 mm정도의 작은 예측오차범위를 보이고 있으며 본 수치해석모델이 전체적인 경향을 잘 예측할 수 있다고 판단하였다.

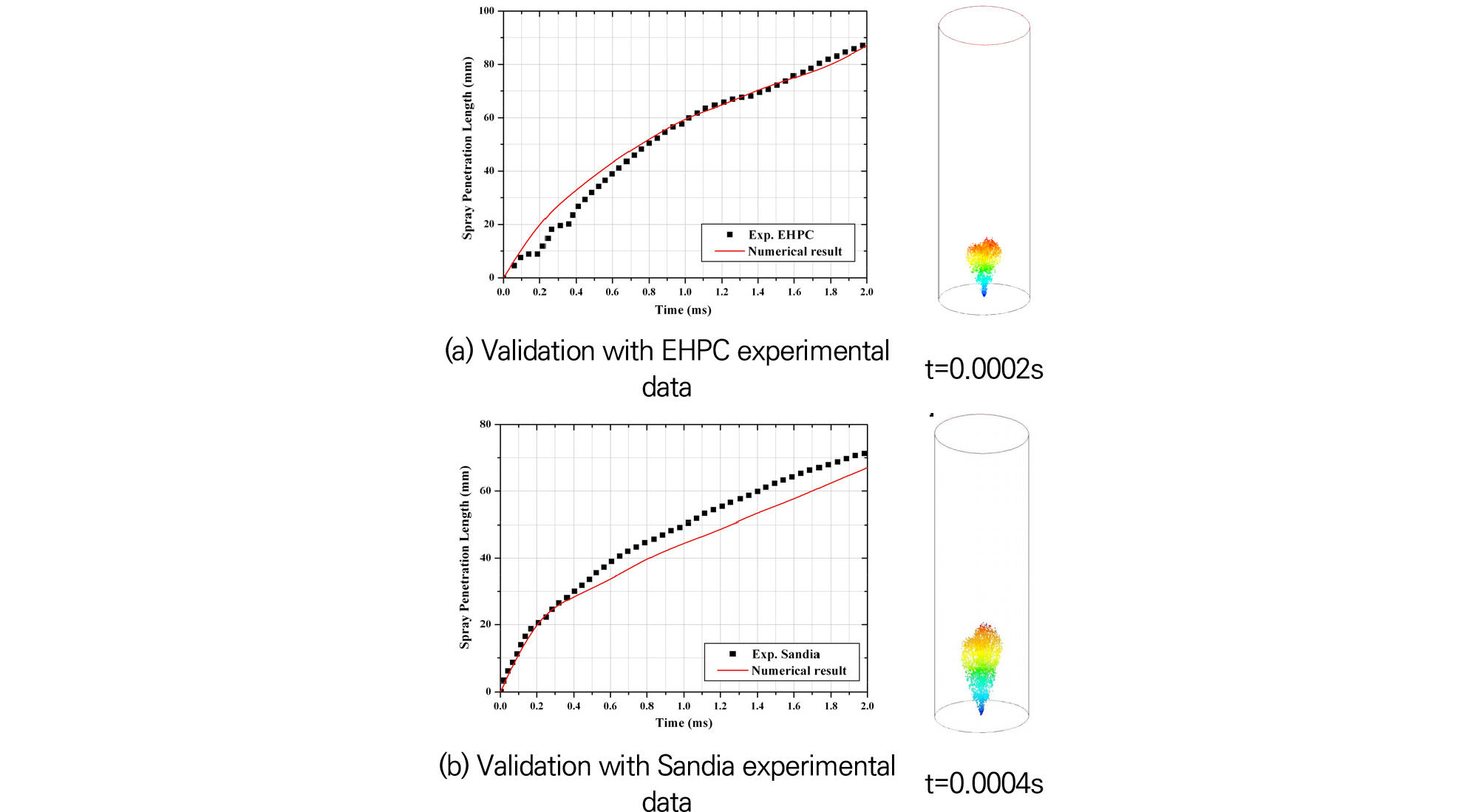
Fig. 5.

Comparison of spray penetration length between numerical result (lines) and experimental data (symbols) [20].

에탄올 연료의 분사 후 발생되는 액적의 크기를 비교하기 위하여 Likun[21] 등에 의하여 수행된 에탄올의 연료분사 액적크기측정 실험조건을 모사하여 수치해석을 진행하였고 그 결과를 Fig. 6에 비교하여 나타내었다. Fig. 6을 살펴보면 대표적으로 액적의 크기를 나타내는 Sauter Mean Diameter(SMD)크기가 각 축 방향 거리에서 실험결과와 근사하게 예측하고 있음을 알 수 있다. 그러나 반경방향으로의 액적분포와 최소 크기의 SMD는 정확히 예측하지 못하는 결과를 보였다. 그럼에도 각 축 방향 거리에서 발생하는 SMD의 최대 크기와 분포는 전반적으로 잘 예측하고 있어 본 연구에 위 Spray 모델을 적용하여 에탄올 MILD연소에 대한 수치해석을 진행하였다.

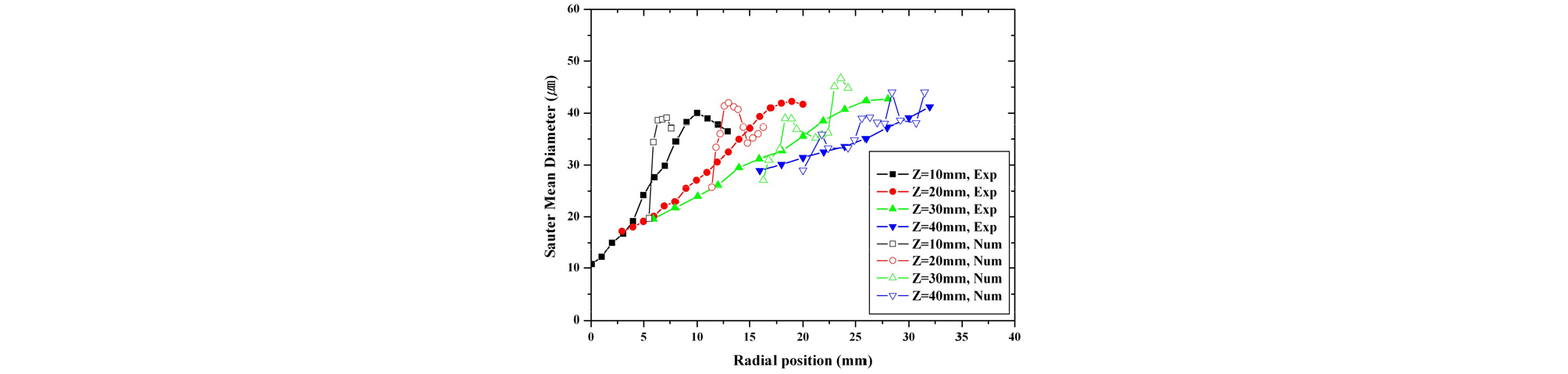
Fig. 6.

Comparison of sauter mean diameter between numerical result (blank dot) and experimental data (solid dot)[21].

3.2 공급유속변화에 따른 에탄올 MILD 연소특성 분석

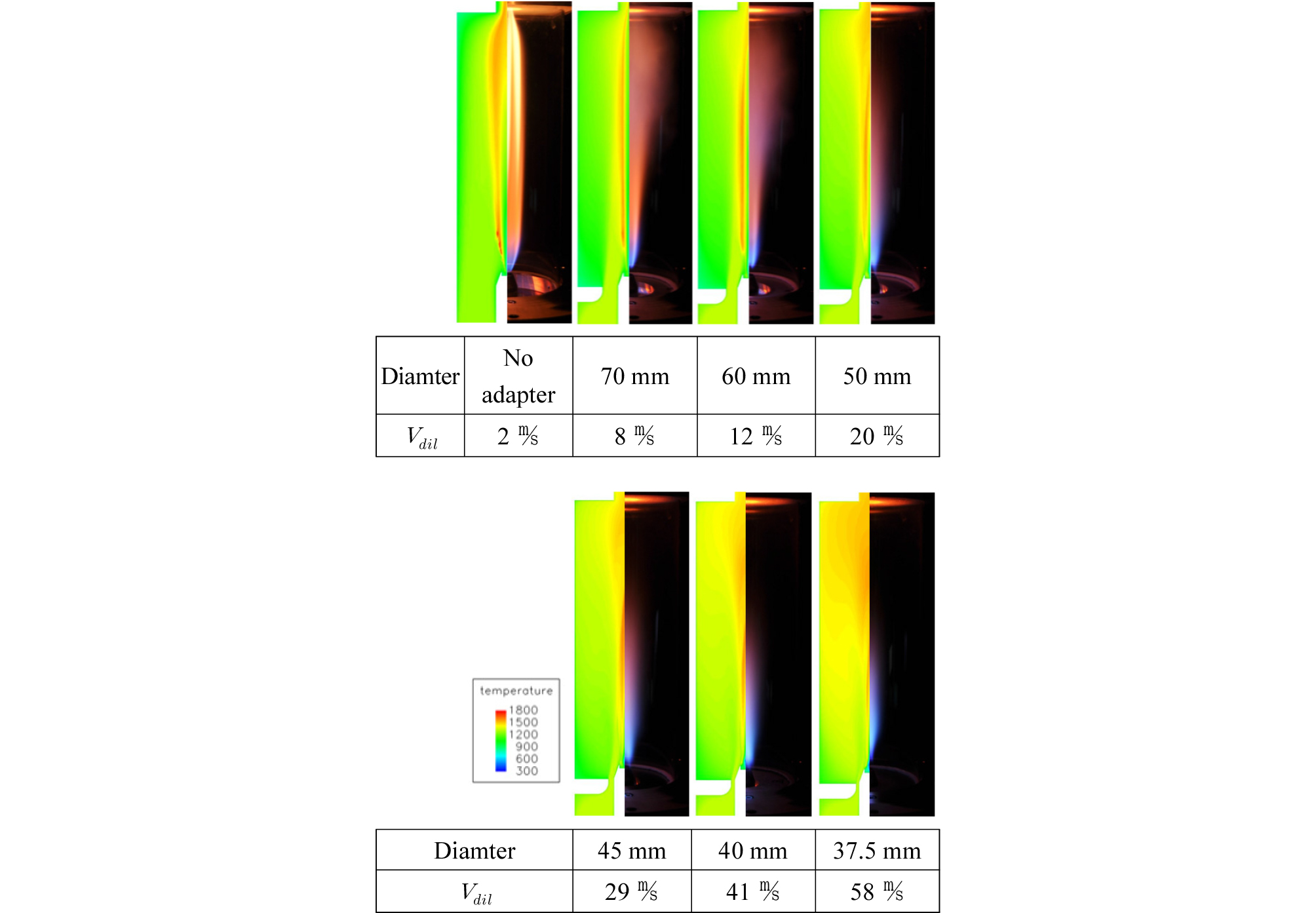
Velocity control adapter의 적용을 통한 희석가스의 공급유속변화는 에탄올분무 연소화염을 밀폐시스템 안에 형성되게 하고 MILD연소에 가까운 화염을 형성하게 하는 매우 중요한 설계요소이다. 따라서 산소농도 7%조건에서 공급유속변화에 따른 에탄올 MILD연소에 대한 수치해석을 수행하였고 온도분포해석결과를 실험을 통해 얻은 화염이미지와 비교하여 Fig. 7에 나타내었다. 수치해석결과 공급유속이 증가함에 따라 발생되는 고온의 온도분포영역이 유동장의 하단부로 이동되어 위치하게 되며 실험결과를 통해 촬영된 오른쪽 사진과 같이 화염길이가 짧아지는 현상과 동일한 결과를 예측하였다. 58 m/s의 가장 빠른 공급유속조건에서 화염의 위치에 발생되는 고온영역은 짧고 얇게 형성되지만 유동장의 상부에 고온영역의 분포가 넓게 형성되는 현상을 볼 수 있다. 이러한 결과는 실험을 통한 화염이미지 촬영으로는 확인할 수 없었던 특징으로 MILD연소에 가까운 화염의 형성으로 인해 반응영역의 온도분포가 상대적으로 고르게 분포되었다고 판단된다.

Fig. 7.

Comparison of between numerical results of temperature distribution (left) and experimental flame images (right).

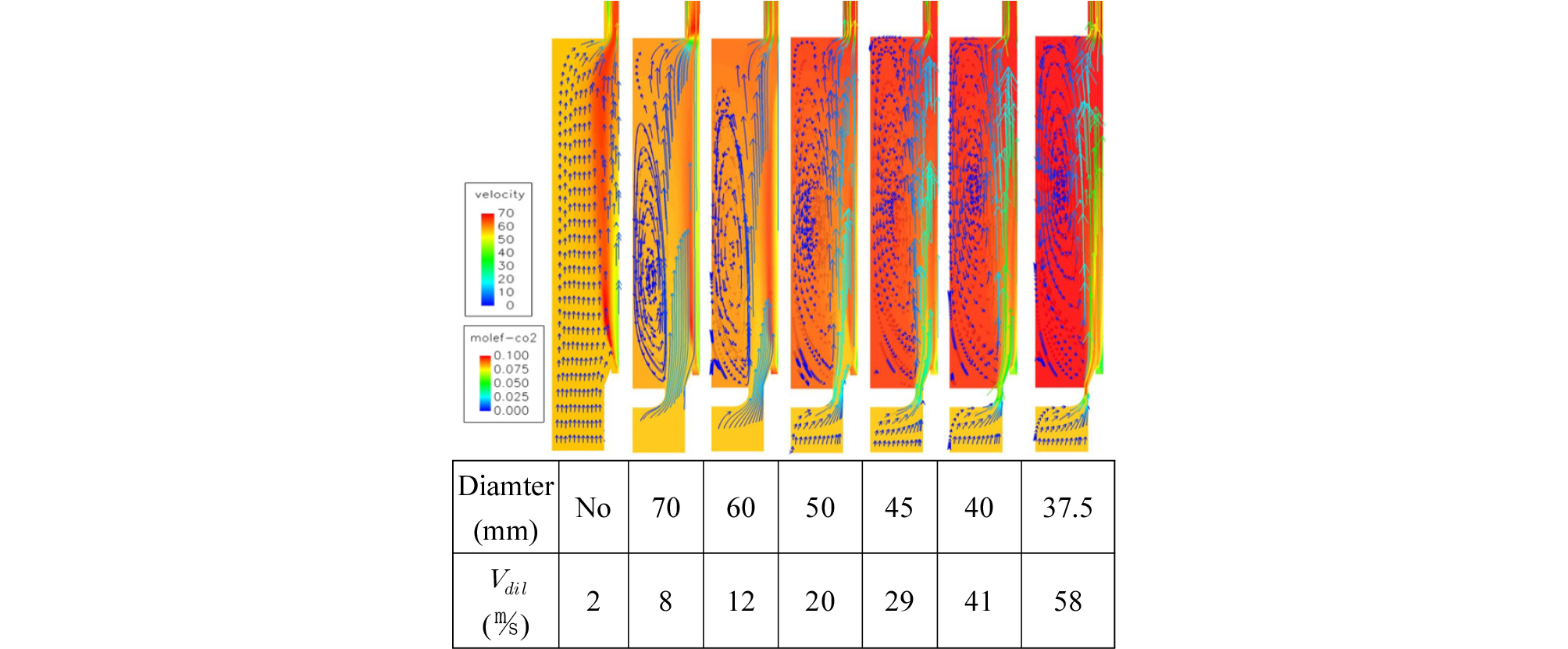
공급유속이 증가하며 MILD연소가 형성되는 이유를 분석해보기 위하여 Fig. 8에서 배기가스를 대표하는 $C{O}_2$분포와 속도벡터를 통하여 유동특성을 살펴보았다. Fig. 8의 속도벡터를 살펴보면 velocity control adapter의 적용 전에는 재순환유동이 전혀 발생하지 않는 것을 확인할 수 있다. Velocity control adapter를 적용하면 연소장 내부에 재순환 유동이 발생하게 되고 velocity control adapter의 직경이 감소하며 희석가스의 공급유속이 증가됨에 따라 발생하는 재순환 유동의 코어가 상부로 이동되며 점차적으로 강한 재순환유동이 형성되었다. 또한 재순환 유동이 강하게 형성됨에 따라 연소장 내부의 $C{O}_2$분포가 균일해지고 농도가 증가되는 결과를 보였다.

Fig. 8.

Velocity vector based on $C{O}_2$ contour regarding the different velocity of dilution gas.

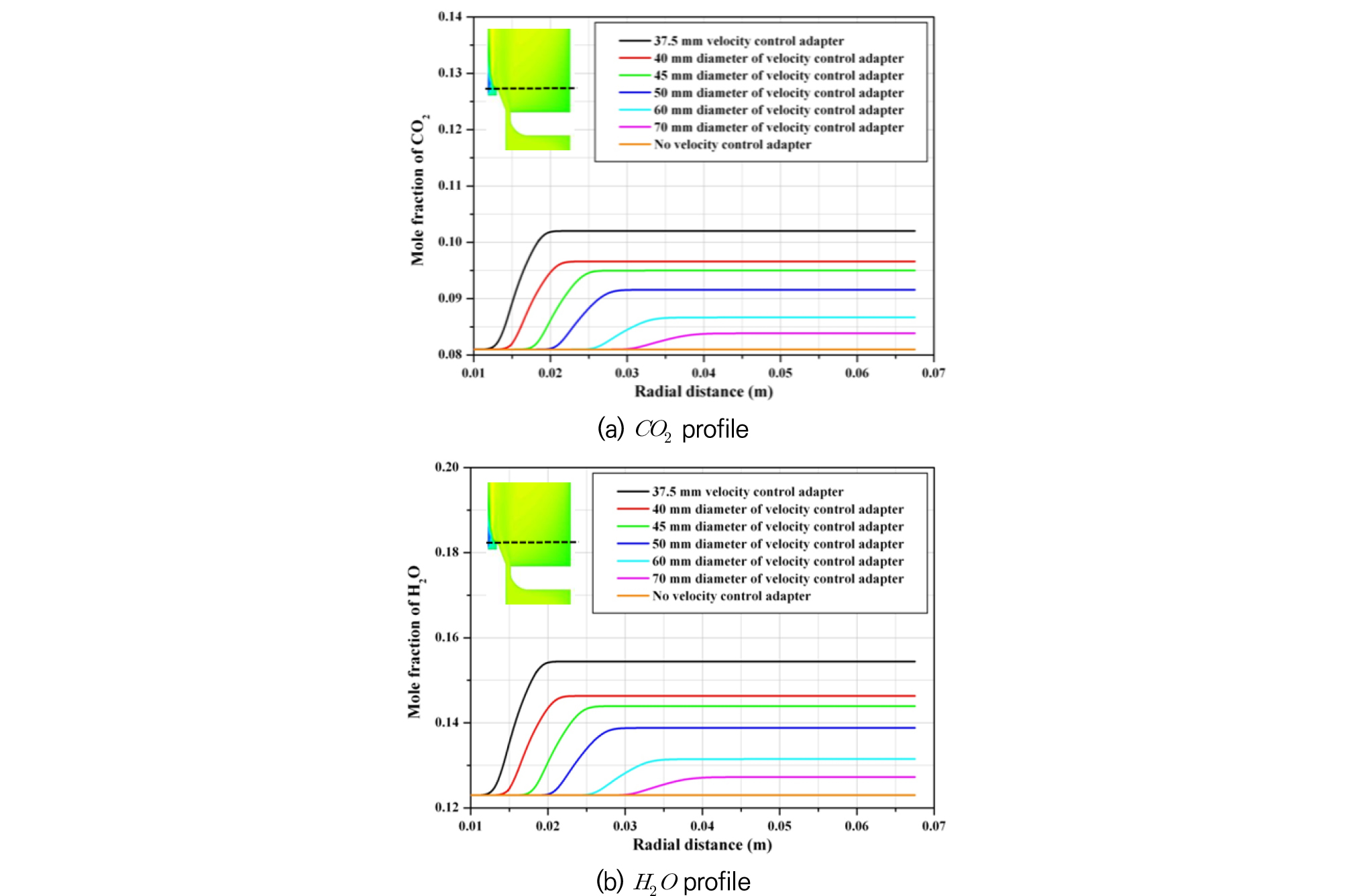
이러한 재순환유동을 통해 증가되는 희석율을 살펴보기 위하여 노즐 상단의 line plot을 통하여 보다 자세히 살펴보았다. Fig. 9 (a)에 나타낸 $C{O}_2$의 경우 에탄올 분사노즐의 끝 지점에서 희석가스의 공급유속이 증가함에 따라 분포되는 $C{O}_2$의 몰분율이 증가되는 것을 확인하였다. 다른 연소 후 재순환가스인 $H_{2}O$ 분포도 마찬가지로 Fig. 9 (b)와 같이 공급유속이 증가되며 연소장 내부에서 재순환되는 $H_{2}O$ 몰분율이 증가되는 것을 볼 수 있다.

Fig. 9.

$C{O}_2$ and $H_{2}O$ profiles regarding the different diameter of velocity control adapters at the nozzle tip.

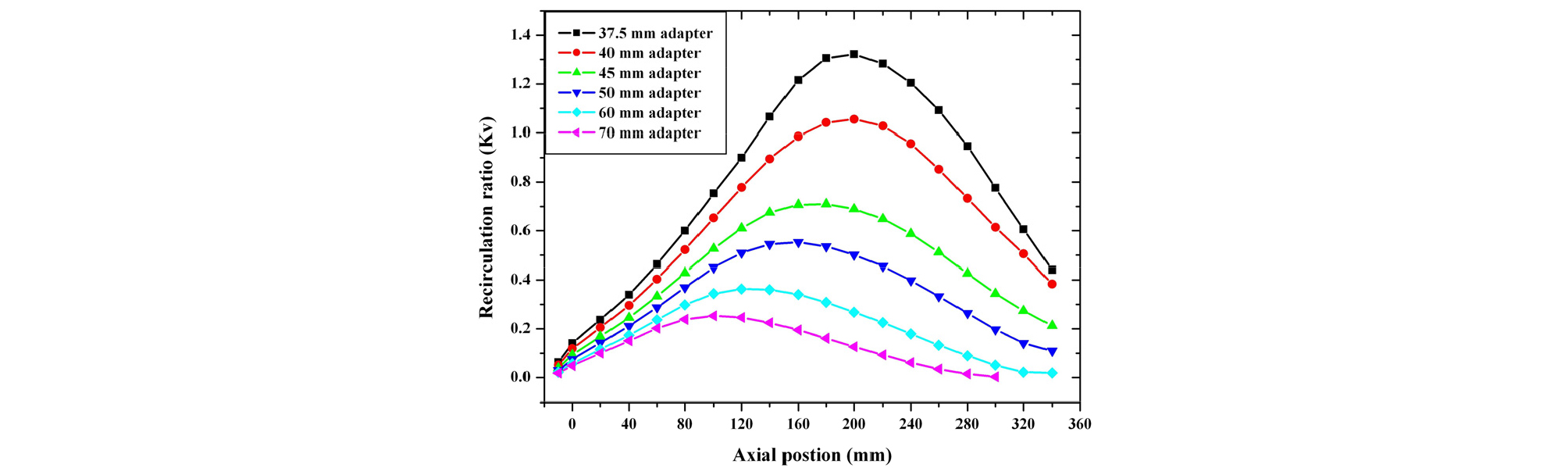
발생되는 재순환 유동의 강도를 비교하기 위하여 앞서 Wünning에 의해 정의된 재순환률($K_V$) 식 (1)을 통하여 유동을 통한 $K_V$를 계산하였다. $K_V$는 Z-축 방향으로 20 mm간격에 대하여 각각 계산되었으며 그 결과를 비교하여 나타낸 Fig. 10을 살펴보면 velocity control adapter의 직경이 감소함에 따라 발생되는 $K_V$의 크기가 증가하며 $K_V$곡선 피크의 위치가 연소장 상류로 이동하는 특징을 나타내었다. 직경 37.5 mm의 velocity control adapter조건에서 연소장의 높이 200 mm지점에서 $K_V$ 1.3으로 가장 높은 값을 나타내었다. 이러한 결과는 Fig. 1에 나타낸 MILD연소영역의 $K_V$조건보다 작은 값이다. 그러나 하단부의 1차 연소를 통하여 산소농도가 낮은 희석가스가 공급되므로 산소농도가 희석되는 정도를 재순환율로 계산하고 그에 더해 공급유속의 증가로 인하여 발생하는 유동의 재순환율을 합하면 $K_V$가 7로 증가함으로 58 m/s의 공급유속조건에서 재순환율 $K_V$조건이 에탄올의 MILD연소영역에 해당되었다.

Fig. 10.

Recirculation ratio ($K_V$) regarding the different velocity of dilution gas.

3.3 산소농도변화에 따른 에탄올 MILD 연소특성 분석

희석가스의 산소농도변화에 따른 에탄올 MILD연소특성을 분석하기 위하여 가장 빠른 공급유속조건인 직경 37.5 mm velocity control adapter 조건에서 희석가스의 산소농도를 6, 7, 8, 9%로 변경하여 수치해석을 진행하였다.

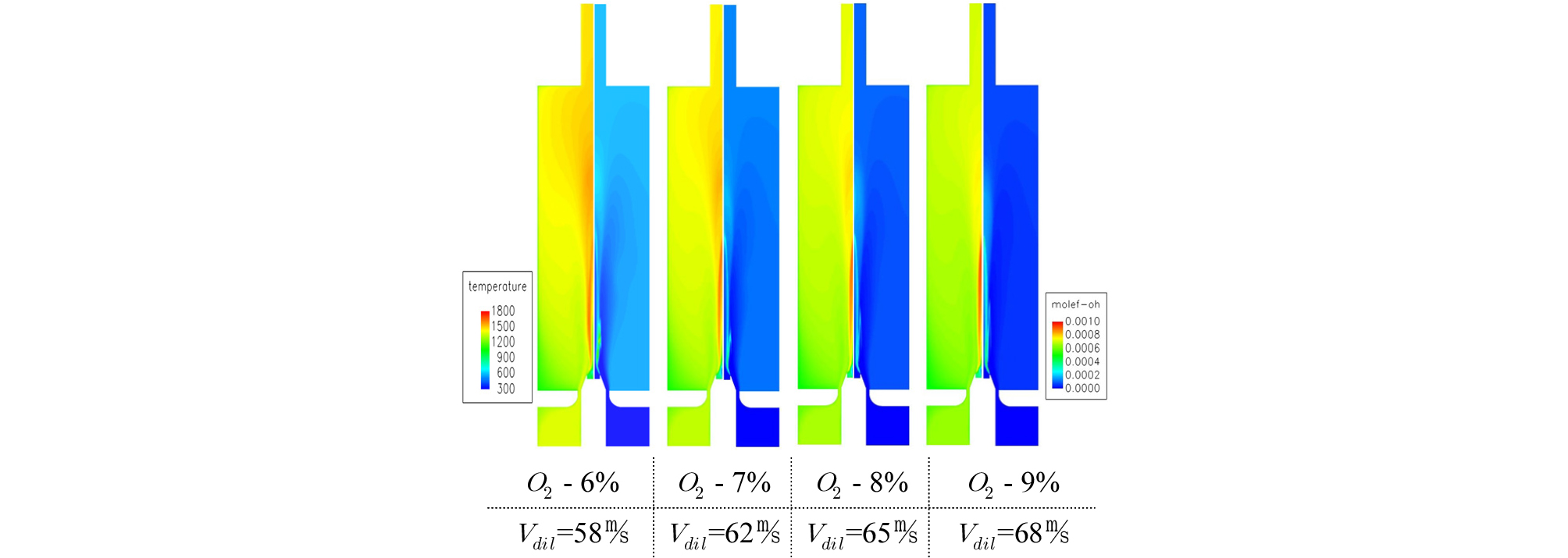
Fig. 11에는 산소농도변화에 따른 온도분포와 OH*의 분포를 비교하여 나타내었다. 왼쪽의 온도분포결과를 살펴보면 산소농도가 9%에서 6%로 감소하는 경우 발생하는 고온의 영역이 보다 길어지고 연소장 상부에 넓게 형성되는 경향이 나타났다. 희석가스의 산소농도가 증가함에 따라 고온영역의 길이가 짧아지고 온도가 증가되는 것을 확인 할 수 있다. Fig. 11 오른쪽의 OH* 분포를 살펴보면 희석가스의 산소농도가 감소함에 따라 연소를 통해 발생되는 OH*의 강도가 낮아지며 연소장에 전반적으로 균일하게 OH*가 분포되는 것을 알 수 있다. 산소농도 6%의 경우 OH* 반응영역의 전체적으로 분포하며 연소장 내부에서 체적연소(Volume combustion)를 형성하는 MILD연소의 특징을 나타내고 있다.

Fig. 11.

Comparison of temperature distribution (left) and OH* distribution (right) for different oxygen concentration.

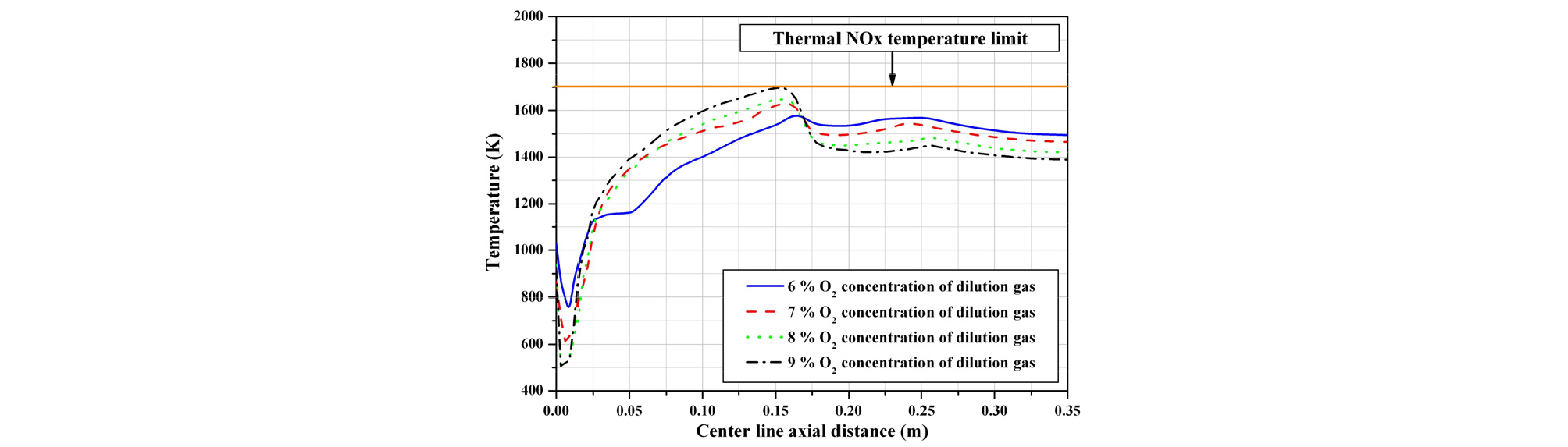
Center line에서의 축 방향 온도분포를 비교하여 나타낸 Fig. 12를 살펴보면 산소농도 7, 8, 9%의 경우 연소장의 0.15 m지점을 경계로 center line의 온도분포가 급격히 낮아지는 경향을 보였다. 반면 희석가스의 산소농도가 6%로 감소함에 따라 발생하는 연소화염의 최고온도가 낮아지며 온도분포가 연소장의 상부에 이르기까지 비교적 균일하게 분포되는 것이 확인되었다.

Fig. 12.

Comparison of temperature profile at the center line for different oxygen concentration.

3.4 에탄올 MILD 연소의 배기가스배출 특성 분석

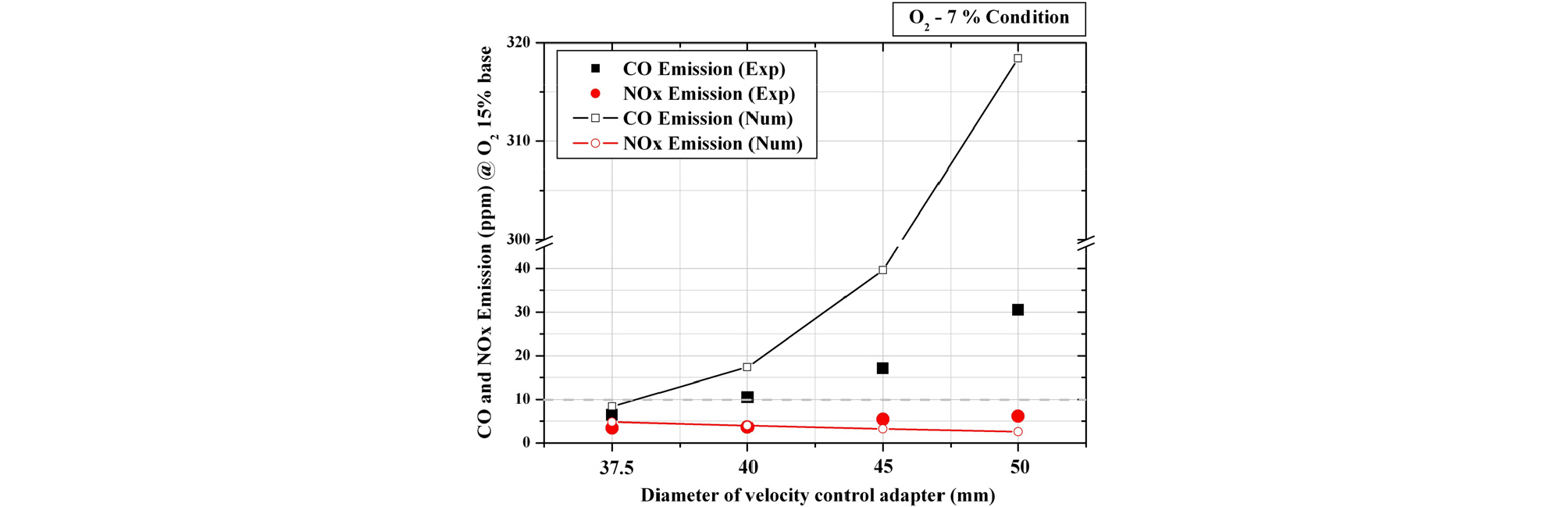
수치해석을 통하여 계산된 각 조건에서의 배기가스배출특성을 실험결과와 비교하여 Fig. 13과 Fig. 14에 각각 비교하여 나타내었다. Fig. 13은 velocity control adapter의 직경변화에 따른 CO 및 NOx의 배출특성을 나타내었다. CO의 경우 수치해석결과가 실험결과에 비하여 과대예측하는 경향을 보였으나 velocity control adapter의 직경이 감소함에 따라 배출되는 CO가 감소하는 경향은 잘 예측하고 있으며 velocity control adapter의 직경 37.5 mm 조건에서는 실험결과와 매우 근사한 값을 보였다. NOx의 경우는 실험결과와 마찬가지로 모든 공급유속조건에서 10 ppm미만의 single digit 수준의 낮은 배출특성을 보였다.

Fig. 13.

Comparison of CO and NOx emission characteristics between numerical results and experimental results for different diameter of velocity control adapter.

Fig. 14.

Comparison of CO and NOx emission characteristics between numerical results and experimental results for different oxygen concentration.

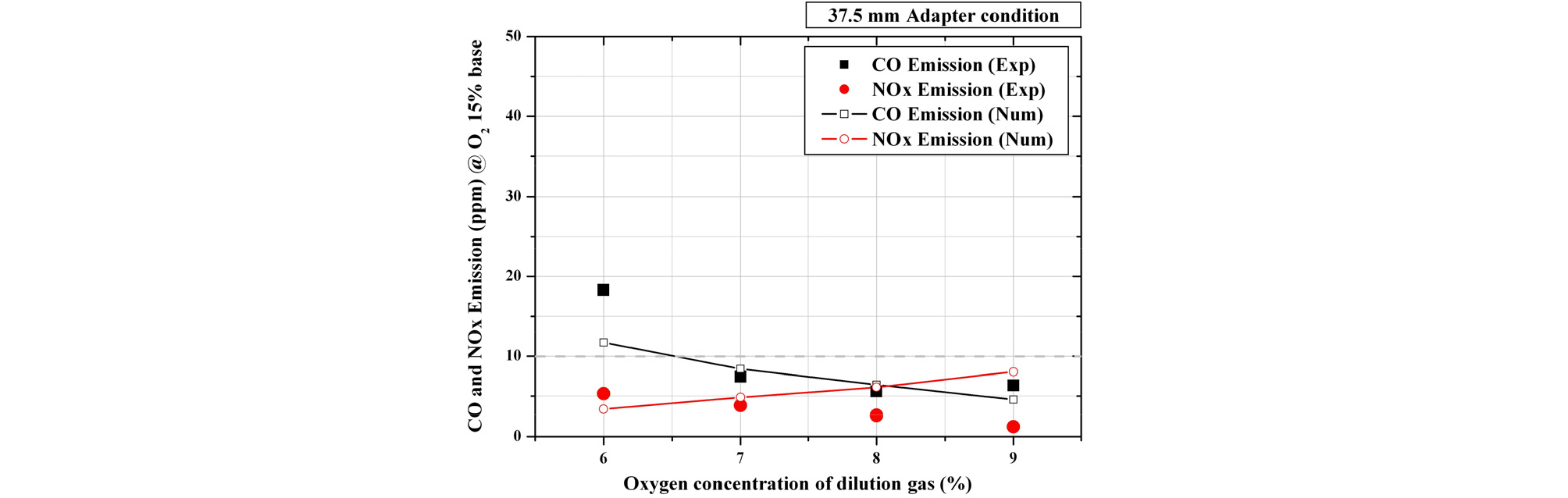
희석가스의 산소농도변화에 따른 CO 및 NOx의 배출특성을 비교한 Fig. 14를 살펴보면 CO의 경우 수치해석결과가 실험결과의 배출량과 산소농도변화에 따른 배출특성 경향을 비교적 잘 예측하였다. 하지만 산소동도 6% 조건의 실험결과의 경우 CO의 배출량이 다른 조건에 비하여 크게 증가된 값을 보였으며 NOx의 경우에도 산소농도가 낮아짐에 따라 NOx 배출량이 감소되는 일반적인 MILD연소 현상과는 반대되는 결과를 보였다. 이러한 이유는 실험순서를 산소농도가 높은 조건부터 시작하여 낮은 조건으로 변경하며 진행함에 따라 당량비 조건이 증가하고 시스템이 가열되며 다른 산소농도 실험조건에 비하여 높은 분위기 온도에서 반응이 일어남으로 NOx의 배출량이 산소농도가 낮아짐에도 점차 증가되는 경향으로 측정된 것으로 사료된다. 반면 수치해석의 경우 산소농도가 낮아지며 MILD 연소가 형성됨으로 발생되는 화염온도가 낮아져 NOx의 배출이 감소되는 경향을 잘 모사하였다. 또한 실험을 통해 측정된 NOx의 배출량은 산소농도변화에도 5 ppm 이하의 낮은 배출특성을 보였고 수치해석결과도 마찬가지로 모든 산소농도조건에서 NOx의 배출량은 4 ~ 8 ppm으로 실험결과와 같은 single digit 수준의 낮은 NOx배출특성을 나타내었다.

4. 결 론

바이오에탄올을 가스터빈 연소과정 상황에 적용하기 위하여 외부 공기의 영향을 받지 않는 연소실 시스템에서 고온 희석된 산화제를 통한 에탄올 MILD연소현상에 대하여 FGM을 이용한 3차원 수치해석을 진행하였고 다음과 같은 결론을 도출하였다.

1) 희석가스 공급유속의 증가는 실험결과와 같이 발생되는 에탄올분사화염의 길이가 감소되어 연소로에 안정적으로 형성되게 하며 비교적 균일한 온도분포를 갖는 MILD연소특성을 보였다.

2) 희석가스의 유속이 증가됨에 따라 유동에 의한 재순환율 $K_V$가 증가되고 1차 연소를 통한 낮은 산소농도조건의 재순환율을 합하면 58 m/s의 공급유속조건에서 재순환율 $K_V$가 7이상으로 증가함으로 Wünning이 제시한 MILD연소영역에 해당함을 확인하였다.

3) 희석가스의 산소농도가 6%로 감소하게 되면 발생되는 에탄올연소화염의 최고온도가 1600 K이하로 감소하게 되고 연소로 전체에 비교적 균일한 온도분포를 형성함으로 MILD 연소특성인 Thermal NOx 생성의 근본적인 억제가 가능함을 확인할 수 있었다.

4) 수치해석을 통한 배기가스 배출특성분석결과가 실험결과와 비교적 잘 일치하는 경향을 보였으며 희석가스의 공급유속 58 m/s조건의 모든 산소농도(6-9%)조건에서 10 ppm 미만인 single digit수준의 낮은 NOx배출특성을 보였다.

기호설명

$\varphi$ : Equivalence ratio

$\rho$ : Density

$v$ : Velocity

$p$ : Pressure

$g$ : Gravity

$\nu$ : Kinematic viscosity

$J_j$ : Diffusion flux species

$S_h$ : Source term