1. 서 론
가스터빈 혹은 로켓 추진체에서 발생하는 열음향 불안정성은 공명(resonance) 현상 중 하나로 연소과정 중 발생하는 비 정상적인 열방출률이 연소기 내의 고유 진동수와 동조(in phase)될 때 발생한다[1]. 설계자 입장(designer viewpoint)에서는 연소기 내의 고유 주파수(natural frequency)를 분석하여 비 정상적인 열에너지와 압력파의 탈조(out of phase)를 유도하는 것이 시스템 안정성 확보를 위해 필수적으로 요구된다. 만약 설계단계에서 불안정성 요인을 사전에 제거하지 않거나 안정화 시스템이 도입되지 않은 채로 시스템을 운영한다면 공조현상으로 인해 연소기 내부에 심각한 기계적 결함이 발생하거나 피로 파괴 혹은 폭발로 이어지는 사고를 유발할 수 있다[2].
위와 같은 상황을 미연에 방지하기 위하여 학계에서는 환형 연소기(annular combustor), 스월버너(swirl burner), 헬름홀츠 공명기(Helmholtz resonator), 리케 튜브(Rijke tube) 등 다양한 연소기에서 연소 불안정성 모드를 감쇠시키는 연구를 수행하여 왔다[3], [4], [5], [6]. 특히 본 연구실은 1/4파장 공명기에서 열음향 불안정 발생 메커니즘을 규명하기 위해 다양한 실험적 연구[7], [8], [9], [10], [11]를 수행하여 왔는데, 음향해석 접근 방식은 Searby의 실험적 고찰[12]을 기반으로 하고 있다.
Searby는 1/4 파장의 종파모드(quarter wavelength longitudinal mode)로 여기(excitation)되는 한쪽 끝이 열린 실린더 형태의 공명기에서 하향 전파하는 예혼합 화염의 천이현상을 관측하였다. 그 결과, 화염이 정상파(standing wave)의 배(anti-nodes)에 해당하는 튜브 바닥으로 전파함에 따라 공명기 내 차지하는 기연가스 영역이 넓어지기 때문에 시간에 따른 음향 세기(acoustic intensity)가 상이하게 측정되었다. 그는 음향 세기에 따라 총 4개의 특징적인 화염 형태를 결합 메커니즘(coupling mechanism)과 함께 아래와 같이 제안하였다.
(1)한쪽 끝이 열린 공명기 상부에서 점화된 화염이 하향 전파하며 수력학적 불안정성(hydrodynamic instability)과 함께 압력 섭동이 발생되지 않는 음향적으로 안정된(acoustically stable) 화염.
(2)점화된 화염이 공명기의 길이 방향으로 1/2되는 지점에 도달하였을 때, 압력의 섭동과 화염으로 인한 열방출 섭동 간에 피드백 결합으로 발생되는 일차 열음향 불안정성(primary acoustic instability). 기본적으로 종파(longitudinal wave)를 가지는 음향파로 인해 화염 표면에 생성된 수력학적 불안정성이 억제되고 음향 주파수 주기로 진동하는 평면화염이 관측됨.
(3)평면화염에서 화염 표면에 물결모양(corrugated structure)이 발생하며 급격한 압력증폭 현상을 유발하는 이차 열음향 불안정성(secondary acoustic instability).
(4)이후 급격한 압력 감쇠와 더불어 난류로 천이하는 화염(turbulent).
현재까지 일차 열음향 불안정성의 성장 메커니즘에 대해 많은 연구가 진행되어 왔고, 그 중에서 타당성이 높은 메커니즘으로 압력결합[13]과 가속결합[14]을 꼽을 수 있다. 우선적으로 압력결합은 일차 열음향 불안정성의 성장률은 결합상수(βM)에 비례한다는 메커니즘으로 β와 M은 은 각각 Zel’dovich 수와 Mach 수를 의미한다. 즉, 화염이 높은 Zel’dovich 수를 가지게 되면 외부 온도 변동에 민감하게 반응하기 때문에 음향장 발생으로 인한 온도장 변화에 연소 반응률이 동조하여 변하게 된다. 또한 아음속으로 진행되는 디플래그레이션(deflagration)의 경우, 화염전파속도가 증가할수록 음속(sound speed)과의 간격이 좁혀지기 때문에 음향장과 연소장이 동조하여 섭동할 여지가 충분하다.
반면 가속결합은 점화 직후 화염 면에 발생되는 수력학적 불안정성으로 인해 화염면적 변화를 야기하고, 이로 인해 화염 대를 가로지르는 유입가스의 탈선을 유발한다. 이때 발생되는 국부 유동속도의 변화가 공명기 내 압력 섭동을 촉발하고 시간에 따른 수력학적 불안정성의 변화와 압력 섭동이 동조되어 압력증폭현상을 야기한다고 주장하고 있다. 전술한 두 연구[13], [14]의 주장이 엇갈린 가운데 최근 Yoon 등[7], [8], [9], [10]이 제안한 연구 결과에 따르면 일차 열음향 불안정성은 화염면적 변화에 무관하고 오히려 높은 결합상수를 가지는 가스조성에서 압력 증폭 현상이 민감하게 반응하는 것을 CO2 레이저 조사기법을 통해 실험적으로 확인하였다. 따라서 일차 열음향 불안정성의 메커니즘에 대한 논란은 일단락될 전망이다.
반면, 이차 열음향 불안정성은 Searby[15]와 Denet[16]가 주장한 이차 열음향 불안정성의 고유한 특징인 화염 표면에 발생되는 물결모양의 파수(wave number)와 압력 섭동의 성장률이 비례한다는 주장이 현재까지 가장 유력한 메커니즘으로 간주되고 있다. Searby와 Denet의 메커니즘도 기본적으로는 수력학적 불안정성을 주요 변수로 취급하는 가속결합을 기반으로 하고 있으며 Denet의 연구[16]에 따르면 수력학적 불안정성과 음향장의 강도가 균형을 이룰 때 안정된 평면화염(일차 열음향 불안정성의 포화상태)이 관측된다. 이후 화염이 튜브 바닥 쪽으로 전파함에 따라 압력 섭동의 진폭이 증가하여 두 섭동의 균형은 무너지고 불균형 상태인 파라메트릭 불안정성(parametric instability)을 발생한다고 보고하고 있다. 이러한 두 섭동의 불균형 상태를 “이차 열음향 불안정성”이라고 정의하고 있다.
따라서 본 연구는 Searby와 Denet 등이 제안한 화염 표면에 발생되는 셀(cell)의 파수와 압력 섭동의 성장률의 상관관계를 조사하기 위해 실험적 연구를 수행하였다. 본질적인 연소 불안정성(intrinsic combustion instability)중의 하나인 수력학적 불안정성을 정량적으로 제어하기 위해 CO2 레이저 조사기법[7], [8], [10]을 채택하였다. CO2 레이저를 에틸렌 화염의 미연 가스 측에 조사하게 되면 에틸렌이 CO2 레이저 파장에 선택적으로 반응하기 때문에 국부 가스온도가 증가하고 화염이 레이저가 조사된 영역으로 가속하게 된다. 따라서 화염면적은 레이저 조사 방향으로 신장하게 되고 수력학적 불안정성은 더욱 심화된다. 본 연구는 상기의 실험 방법을 채택하여 이차 열음향 불안정성을 인위적으로 구현하여 Searby와 Denet 등이 제안한 이차 열음향 불안정성 성장 메커니즘에 대해 실험적 검증을 시도하였다.
2. 실험장치 및 방법
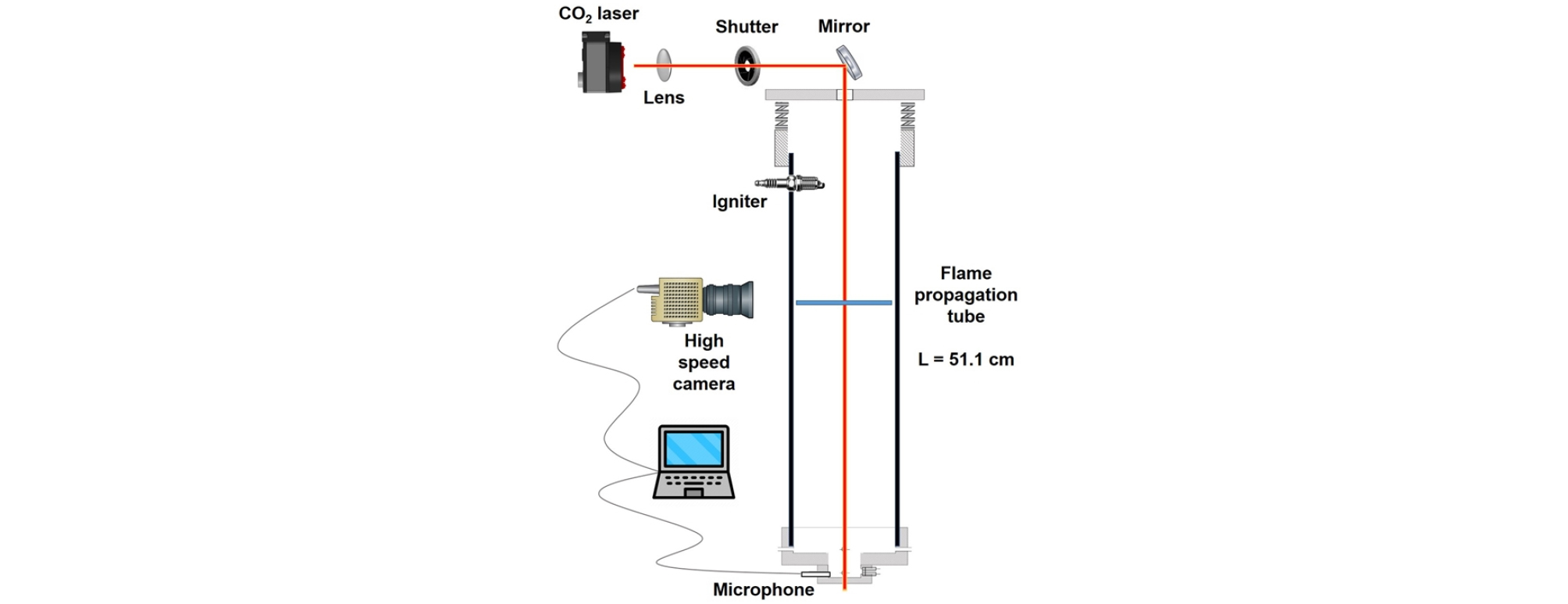
Fig. 1은 실험에 이용된 1/4 파장 공명기의 개략도와 광학 장비를 도시하고 있다. 공명기로 사용된 투명 아크릴 관은 내부 직경이 50 mm, 길이는 511 mm이다. 버너 상단은 전자석(electro-magnet)과 스프링(mechanical spring)으로 구성된 전자동 개패 시스템이 설치되어있다. 개패 시스템이 닫힌 상태에서 예혼합 가스는 대기압으로 충전되고 이후 충전된 가스가 공명기 내에서 안정화될 때까지 5 min가량 대기한다. 스파크 점화기(spark igniter)에서 점화가 시작됨과 동시에 버너 상부의 설치된 개패 시스템이 열리게 된다. 화염 생성 후, 0.7 s 가량 경과된 후에 관내 예혼합 가스는 CO2 레이저에 노출된다. 본 실험에 사용된 가스 조성에서 점화 후 0.7 s일 때 화염은 포화 상태의 일차 열음향 유동장을 발생하게 된다. 실험에 사용된 레이저 빔의 직경과 파장은 각각 3.3 mm과 10.6 µm에 해당하고 압력 변화를 측정하기 위해 마이크로폰(OnosokiM1432)을 공명기 하단에 설치하였다. 화염 가시화를 위해 초고속 카메라로 화염 이미지를 2000 fps 단위로 수득하였다.
실험에서 사용된 예혼합 가스의 조성은 Table 1에 표기하였다. 여기서 SL은 층류화염전파속도, Tb는 단열화염온도, 그리고 βM은 서론에서 전술한 결합상수를 나타낸다. 현재에 사용된 상태량은 USC II 반응 메커니즘을 채택하여 CHEMKIN (Premix code)으로 도출하였다. 본 연구는 레이저 조사기법을 채택하여 평면화염에 인위적으로 수력학적 불안정성을 구현하여 이차 열음향 불안정성을 유도하는 것이 일차적인 목적이기 때문에 레이저를 조사하지 않은 기본화염(default flame)은 이전 연구[7]의 실험결과를 토대로 일차 열음향 불안정성이 발생되는 결합상수, 0.011로 선택하였다. 여기서 β는 12.94, M은 8.8×10-4에 해당하는 값이다.
Table 1. Composition of tested gas mixture
| C2H4 | O2 | CO2 | SL (cm/s) | Tb (K) | βM |
| 0.07 | 0.24 | 0.69 | 21.7 | 2049 | 0.011 |
3. 결과 및 고찰
3.1. 일차 열음향 불안정성
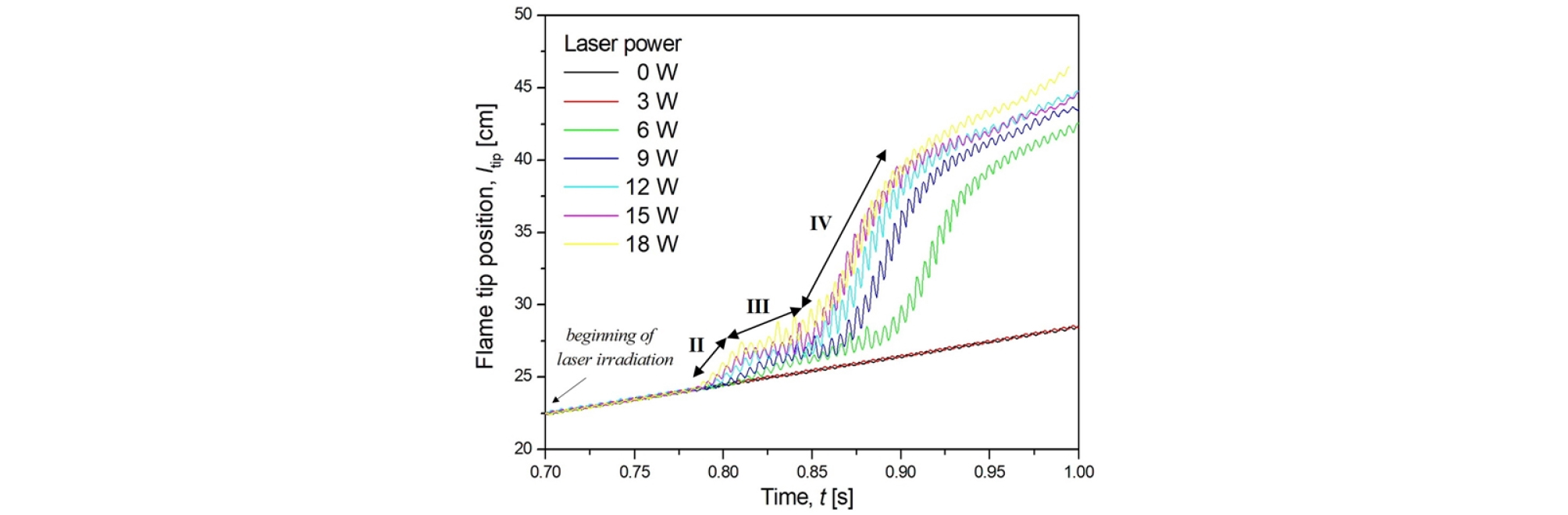
Fig. 2는 시간에 따른 화염 선단위치, ltip, 를 화염 면에 조사된 CO2 레이저 출력에 따라 도시하였다. 여기서 t = 0 s는 화염이 점화된 시간을 나타내며 t = 0.7 s에서 레이저가 조사되었다. 3.1절에서는 레이저가 조사되지 않는 기본화염(default flame)의 화염거동에 대해서만 논의하기로 한다.
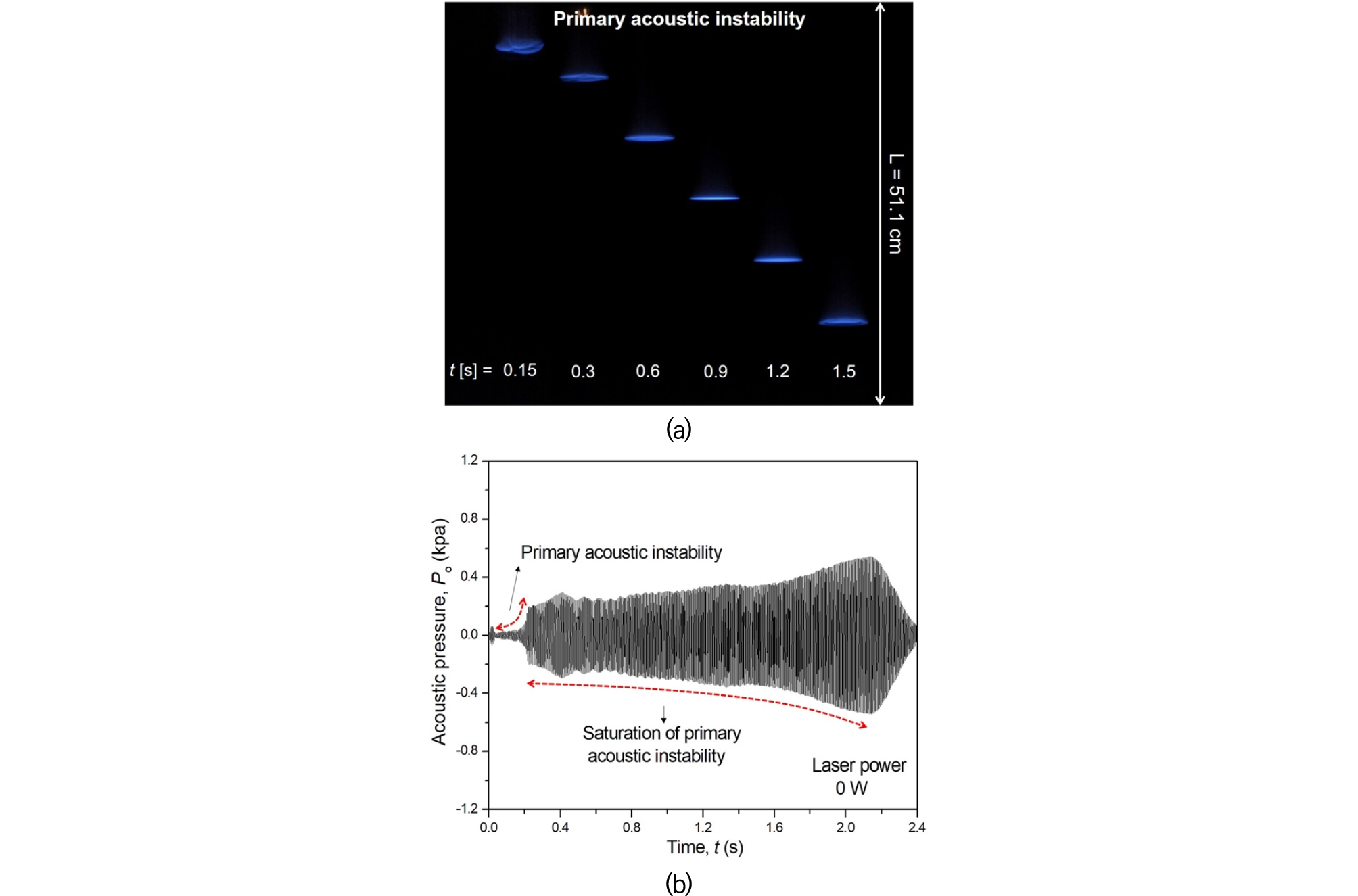
우선 점화 초기, 화염은 미연 가스와 기연가스의 밀도 차에 의해 야기되는 수력학적 불안정성으로 인해 화염 표면에 셀 형태의 굴곡진 화염이 발생하며 튜브 바닥 쪽으로 음향 진동(acoustic vibration)없이 자연스럽게 하향 전파 한다. Fig. 3(a)에 시간에 따른 기본화염의 화염구조를 관찰하기 위하여 튜브 위치에 따른 화염이미지를 시간 별로 나타내었다. 여기서 좌측에 표기된 스케일은 실제 튜브상단에서의 거리에 해당한다. 그림에서 보듯, 점화 직후 0.15 s 지난 시점부터 화염 표면에 발생된 셀의 진폭은 점차 감소하고 작은 소음과 함께 평면화염으로 천이한다. 이때 평균 화염전파속도는 20.34 cm/s으로 층류 화염전파속도인 21.7 cm/s와 매우 유사한 값을 획득하였다.
이러한 원인으로 본 실험은 기본적으로 유량제어 시스템이 없는 정지 유체를 초기 조건으로 채택하고 있고 또한 일차 열음향 유동장이 발생하더라도 음향파는 사인파들의 중첩으로 표현할 수 있기 때문에 이를 준 정상상태(quasi-steady state)로 고려한다면 시간에 따른 변위가 항상 0으로 간주할 수 있다. 따라서 수력학적 불안정성이 억제된 평면화염의 전파속도는 층류 화염전파속도와 유사하게 도출되는 것은 매우 타당한 실험 결과이며 추후 연구를 통해 화염전파속도 측정 방안에 대해 지면을 통해 발표할 예정이다.
시간에 따른 압력변화를 도시한 Fig. 3(b)를 살펴보면, 화염이 생성되는 초기 시간에는 점화 커넬(ignition kernel)이 관측되고 스파크 점화로 인한 잡음으로 인해 미세한 압력변화가 관측된다. 이후 음향진동이 관측되는 0.15 s에서 평면화염이 관측되는 0.3 s까지 측정된 압력 섭동은 배경 잡음(background noise)보다 큰 값을 가지며 압력 섭동의 진폭은 시간에 따라 급격하게 성장한다. 현재의 영역을 “일차 열음향 불안정성(primary acoustic instability)”이라 일컫는다[12], [13]. 이후 압력 성장률의 기울기는 완만하게 증가하다 화염이 튜브 상단으로부터 약 40 cm에 해당하는 지점에 도달하게 되면 화염의 체류시간이 음향 에너지의 손실(acoustic energy losses)을 야기할 수 있는 시간을 초과하게 되어 압력 섭동은 급격히 감소하게 되고 감쇠된 음향파로 인해 화염 형태도 더 이상 평면화염을 유지할 수 없게 된다. 이후 공명기 내의 모든 가연가스를 소비하게 되면 화염은 소화되고 내부에 발생된 음향장도 사라지게 된다. 여기서 평면화염을 유지하며 완만한 압력증폭을 보이는 구간을 “일차 열음향 불안정성의 포화상태(saturation of primary acoustic instability)”라고 정의[12], [13]하는데 압력파와 열방출률의 섭동으로 인한 피드백 결합이 음향손실과 적절히 균형을 이루기 때문에 발생하는 것으로 이해될 수 있다.
음향 에너지 손실을 유발하는 2가지 요인은 첫째, 외부로 노출된 튜브 상단으로 음향 에너지가 소산되는 복사 손실(radiative losses)과 둘째, 튜브 벽면에서 점성 경계층과 열 확산 경계층 내에서 발생하는 벽면 손실(wall losses)을 꼽을 수 있다[7]. 이러한 음향 에너지 손실의 증감은 이차 열음향 불안정성의 발생을 결정하는 매우 중요한 인자로, 만약 어떠한 외부 요인으로 인해 수력학적 불안정성과 음향장 간의 불균형을 초래하게 된다면 화염 표면에 셀 불안정성이 발생하게 되고 화염 면을 가로지르는 유입가스의 유선(streamline)의 변형을 야기하게 된다. 만약, 가속결합[14]을 기반으로 한 화염면적 변화가 이차 열음향 불안정성의 성장률에 지대한 영향[15], [16]을 미친다면 압력증폭현상으로 인해 발생된 음향 에너지가 음향 에너지 손실량을 초과하여 이차 열음향 불안정성의 발생을 유도할 것으로 예상된다. 따라서 다음 절에서는 본 연구에서 채택된 기본화염에 CO2 레이저를 조사하여 인위적인 화염면적 변화를 유도한 뒤 이차 열음향 불안정성 발생 여부와 압력 섭동의 성장률을 조사하기로 한다.
3.2. 이차 열음향 불안정성
본 절에서는 3.1절에서 논의한 기본화염에 레이저 조사하여 이차 열음향 불안정성을 인위적으로 구현하여 압력 성장 메커니즘에 대해 논의하기로 한다. 시간에 따른 화염 선단위치를 도시한 Fig. 2를 재 상기하면 기본화염이 점화 후 0.7 s 경과된 시점, 즉 튜브 상단으로부터 22.5 cm 지점에 도달하였을 때 레이저 광을 화염 면 중심에 조사하였다.
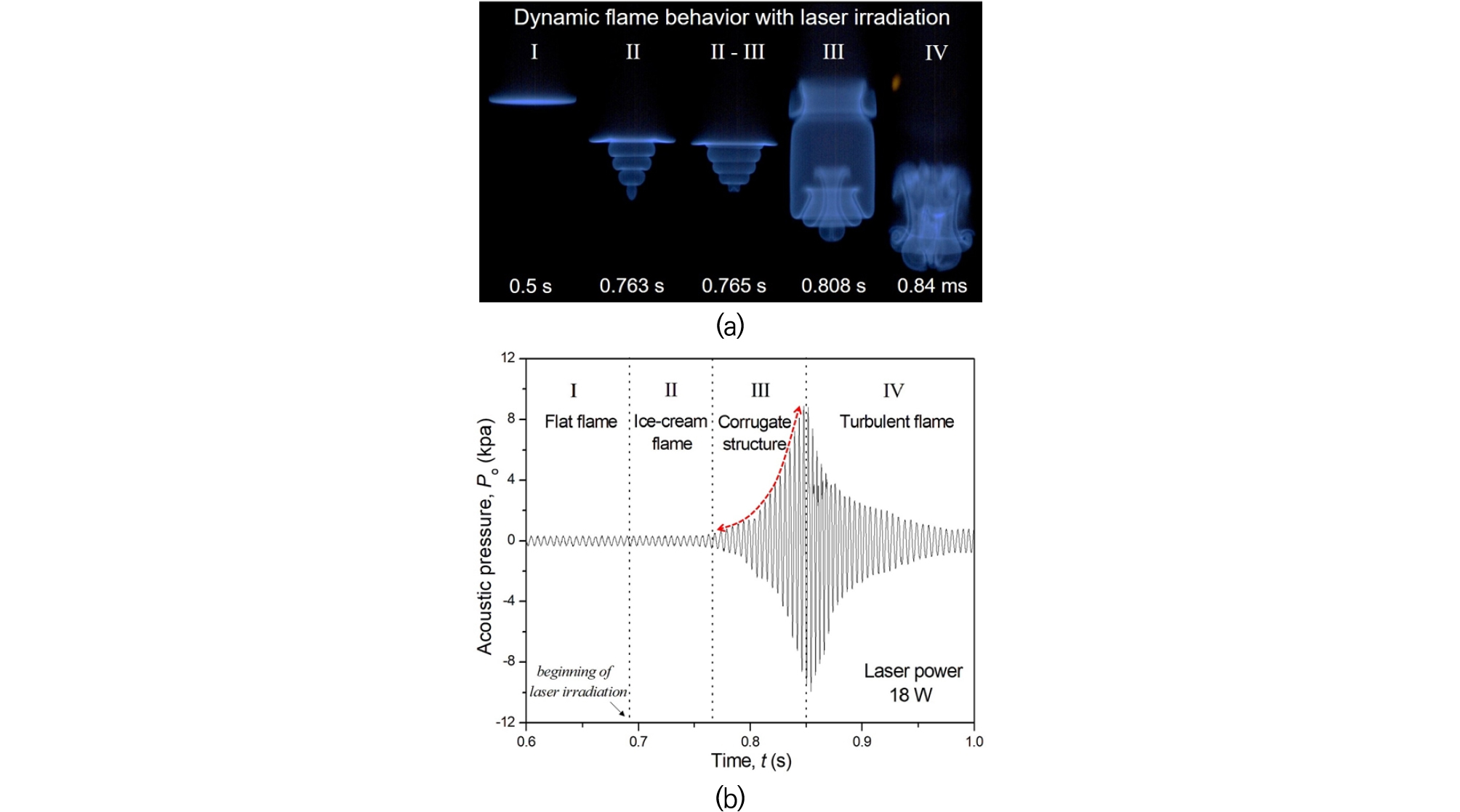
Fig. 4(a)와 (b)는 레이저 출력 18 W조건에서의 시간에 따른 화염거동 이미지와 압력변화를 각각의 영역 별로 도시하였다. 우선 CO2 레이저를 기본화염(Fig. 4(a), I)에 조사하게 되면 에틸렌 가스가 선택적으로 반응하게 되고 화염선단의 국부 가스온도가 증가하게 된다. 따라서 화염 면 중심으로 부터 국부 화염전파속도가 증가하여 Fig 2에서 도시한 바와 같이 레이저 조사 이후 0.1 s 경과된 시점부터 급작스런 가속을 하게 된다. 이때 음향파는 기본적으로 종파로 구성되어 있고 레이저를 이용한 국부가열은 단일방향으로 열전달하는 특성이 있기 때문에 화염 형상도 아이스크림 모양의 매우 특징적인 모양으로 변하게 된다(Fig. 4(a), II). 여기서 주목할 점은 화염면적 변화가 급격히 이루어짐에도 불구하고 압력 섭동의 증폭은 전혀 변화하지 않는다는 것이다(Fig. 4(b), II). 즉 일차 열음향 불안정성의 성장률은 Pelcé 와 Rochwerger[14]의 주장과는 달리 화염면적 변화와는 무관하다는 것을 알 수 있고 이러한 실험 결과를 이전 문헌에서 발표한 바 있다[7]. 이후 화염선단에 이차 열음향 불안정성 발생의 전조현상(precursor)인 오목한 화염(Fig. 4(a), II-III)이 발생하게 되면 평균 화염전파속도는 감소하고(Fig. 2) 화염 면은 심하게 굴곡진 형태(Fig. 4(a), III)를 띄며 압력 섭동의 폭발적인 증가(Fig. 4(b), III)를 보인다. 이와 같이 물결모양(corrugated structure)의 화염구조, 평균 화염전파속도의 감소, 그리고 폭발적인 압력 섭동의 증가는 전형적인 이차 열음향 불안정성의 특징과 일치한다고 볼 수 있다[7], [12], [14], [15]. 마지막으로 물결모양의 화염구조가 붕괴되고 평균 화염전파속도의 증가와 더불어 난류 화염으로 천이(Fig. 4(a), IV)하게 되는데, 이때 압력 섭동의 진폭은 큰 폭으로 감소한다(Fig. 4(b), IV). 이는 난류화염으로 인해 발생된 작은 화염 파편들이 급격히 증가함으로써 관 내 복사 열손실이 증가하고, 벽면으로 음향손실이 상승하기 때문이라고 판단된다.
한편, 레이저 조사기법은 단순히 기연가스의 국부가열로만 고려할 것이 아니라 볼록한 화염 면을 따라 유입가스 유동의 탈선을 유발하기 때문에 수력학적 불안정성을 정량적으로 제어할 수 있는 실험방안으로 생각할 수 있다. 따라서 레이저 출력에 따라 화염면적 변화를 실험적으로 제어할 수 있기 때문에 수력학적 불안정성 강도를 인위적으로 제어 가능하다고 볼 수 있다. 이 점을 염두에 두고 논의를 계속하고자 한다.
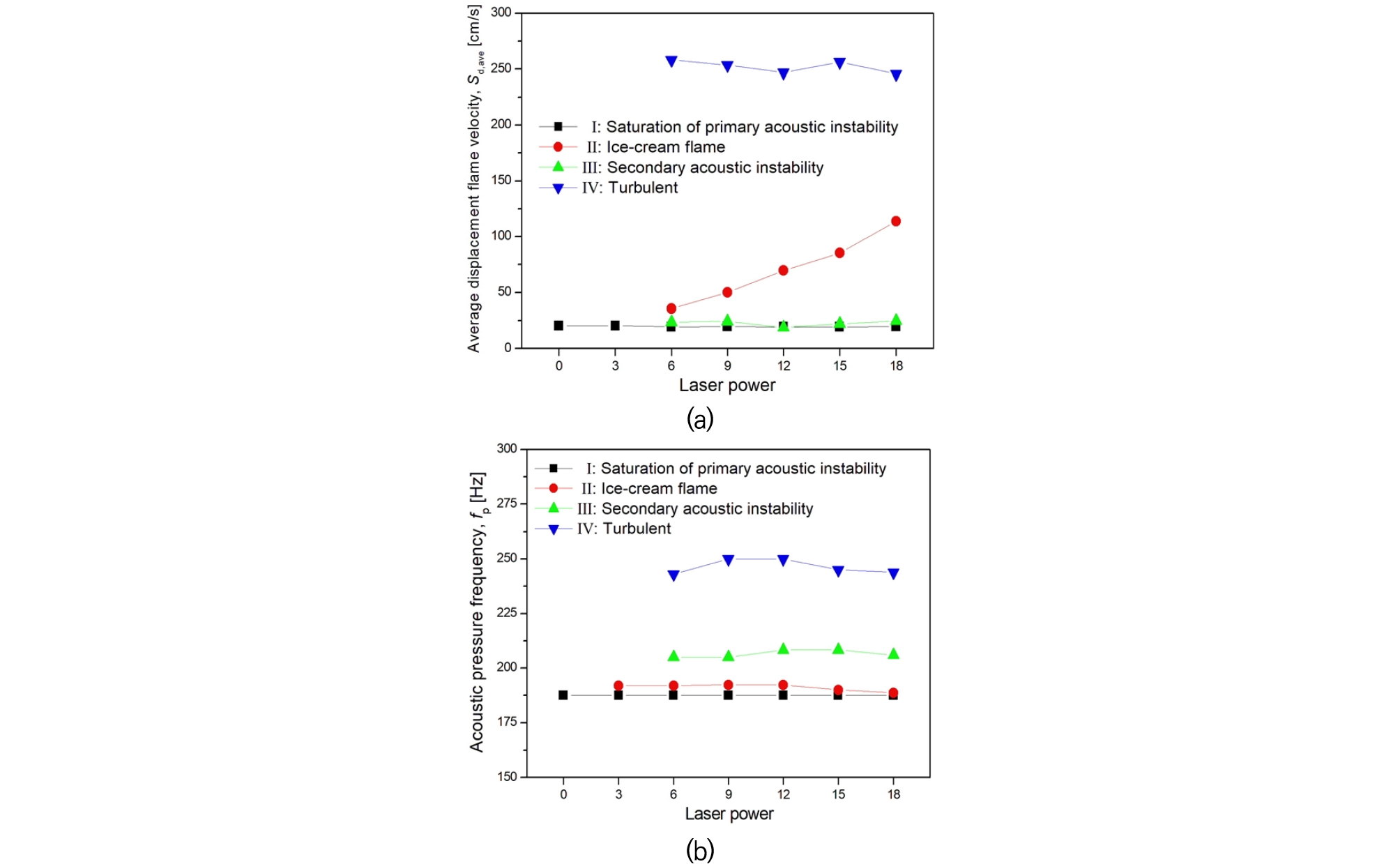
Fig. 5(a)와 (b)는 레이저 출력에 따른 평균 화염전파속도의 변화와 음향 주파수 변화를 각 영역 별로 도시하였다. 현재의 음향 주파수는 측정된 압력정보를 바탕으로 시간 도메인과 함께 FFT 분석 결과를 나타내었다. 그림에서 보듯, 일차 열음향 불안정성이 포화된 영역 I에서는 전술한 바와 같이 층류 화염전파속도인 21.7 cm/s와 유사한 20.34 cm/s로 도출되었고, 화염 면에 CO2 레이저 조사한 영역 II에서는 레이저 출력이 증가함에 따라 평균 화염전파속도가 증가하였다. 급격한 압력 성장률을 보인 영역 III에서는 이차 열음향 불안정성의 특징인 급격한 셀 구조의 화염형태와 빠른 순간 화염전파속도가 관측되어지나 평균 화염전파속도는 일차 열음향 불안정성이 포화된 영역 I과 유사하게 도출되었다. 마지막으로 난류화염 영역인 영역 IV에서는 전술한 바와 같이 평균 화염전파속도가 약 250 cm/s로 급격히 가속되는 것을 확인할 수 있다.
이차 열음향 불안정성의 발생 메커니즘에 대해 추가적으로 논의하기 위하여 압력 섭동의 주파수 변화를 고려하기로 한다. Fig. 5(b)에서 보듯, 영역 I에서는 약 187 Hz의 진동 주파수가 측정되었는데, 이는 1/4파장 공명기에서 정의되는 기본 주파수(fundamental frequency), 168 Hz와 유사한 값이 도출되었다. 기본 주파수는 의 식을 사용하여 획득하였으며, 여기서 c는 공기의 음속(343 m/s)을 가정하였고, L은 공명기의 길이(51.1 cm)로 정의하였다. 영역 II(ice-cream flame)에서도 영역 I과 마찬가지로 기본 주파수와 유사한 약 190 Hz가 도출되었고 이차 열음향 불안정성이 발생하는 영역 III에서는 기본 주파수보다 높은 약 206 Hz가 도출되었다. 특히 영역 III에서는 초고속 카메라로 획득한 화염 진동 주파수가 압력 섭동 주파수의 절반에 해당하는 약 103 Hz가 도출되었는데 이는 기본적으로 이차 열음향 불안정성이 “oscillation”으로 명칭 되는 “Faraday instability”와 유사하다는 이전 연구 결과[17], [18]와 일치한다. 반면 일차 열음향 불안정성의 경우에는 압력 섭동 주파수와 화염 진동 주파수가 정확히 일치하였고, 이것은 이전 문헌[17]에서도 “oscillation”과 달리 “pulsation”으로 명명하고 있다. 난류 화염이 발생하는 영역 IV에서는 압력 섭동 주파수가 약 246 Hz로 도출되었다.
Fig. 5(a)와 (b)의 실험 결과를 보면 레이저 출력에 따라 화염면적 변화를 상이하게 한 결과 영역 II에서의 평균 화염전파속도 결과를 제외하고는 모든 평균 화염전파속도와 압력 섭동 주파수가 각 영역 별로 일치하는 것을 알 수 있다. 특히 레이저 출력에 따라 미연가스의 예열 정도가 상이하다는 점을 고려하면 영역 II에서의 평균 화염전파속도는 레이저 출력이 증가함에 따라 빨라지는 관측 결과는 명백한 현상이라고 볼 수 있다. 또한 이차 열음향 불안정성에서 화염면적 변화에 따라 평균 화염전파속도와 압력 섭동 주파수의 차이가 없는 것으로 보아 이차 열음향 불안정성의 성장 메커니즘은 오로지 가속결합[14]으로만 설명될 수 없다는 점을 시사한다고 볼 수 있다.
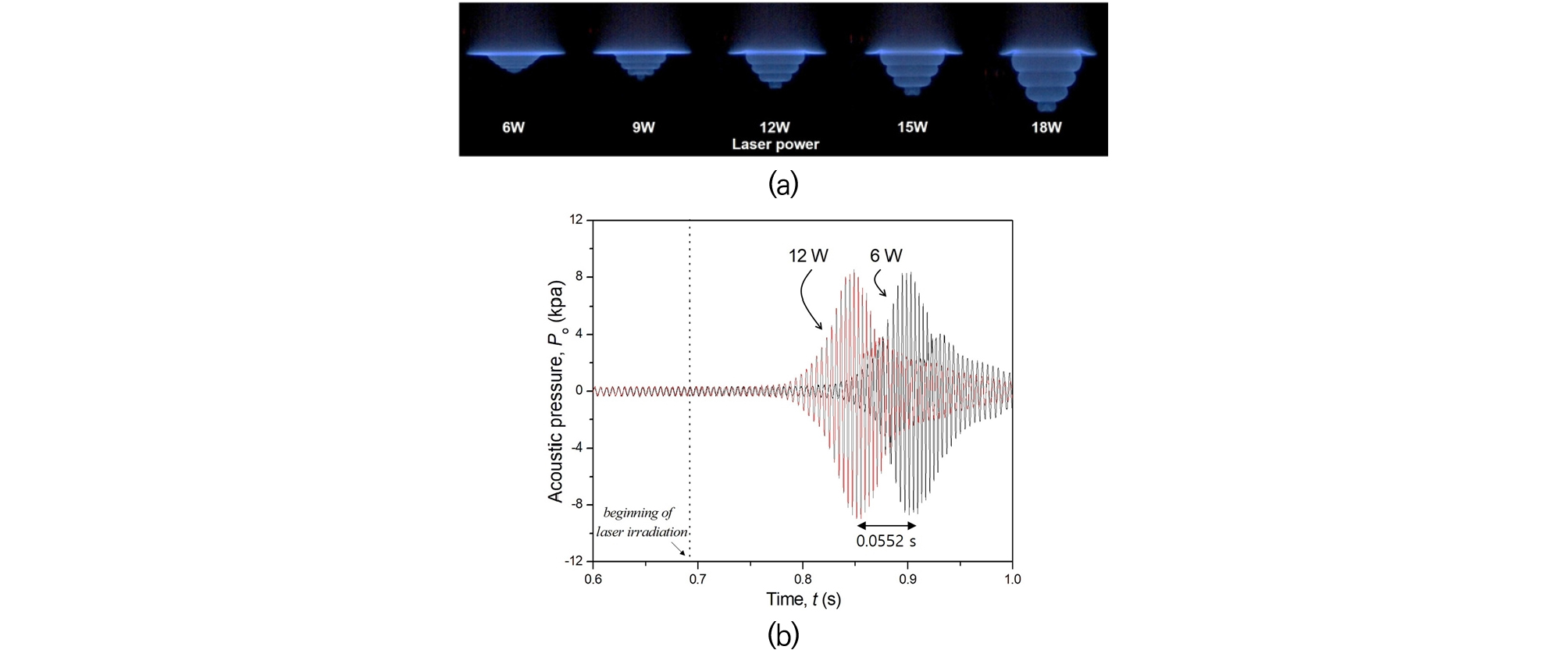
이 점을 보다 명확하게 하기 위하여 Fig. 6(a)에 이차 열음향 불안정성의 전조 현상인 화염 선단에 오목한 화염이 발생했을 때의 화염 이미지를 레이저 출력 별로 나타내었다. 그림에서 보듯, 레이저 출력이 증가함에 따라 전체 화염면적이 넓어지고 화염 면에 발생한 파수(wave number)가 감소되는 것을 알 수 있다. Pelcé 와 Rochwerger[14]의 이전 연구 결과에 따르면 음향 성장률(growth rate)은 축약파수(reduced wave number)와 비례관계가 있다고 보고한 바 있다. 따라서 본 연구 결과에서도 이전 연구결과와 일치하는지 검증하기 위해서 Fig. 6(b)에 시간에 따른 압력 변화를 레이저 출력 6과 12 W에 대해서 나타내었다. 그림에서 보듯, 동일 시간(점화 후 0.7 s)에 레이저가 화염 면에 조사되었음에도 불구하고 압력이 증폭되는 시점은 12 W 출력인 경우가 6 W인 경우보다 0.0552 s 빠르게 나타났다. 그럼에도 불구하고 압력 섭동의 성장률을 나타내는 마루 혹은 골(anti-node)의 기울기는 레이저 출력에 관계없이 거의 일정한 것을 알 수 있다.
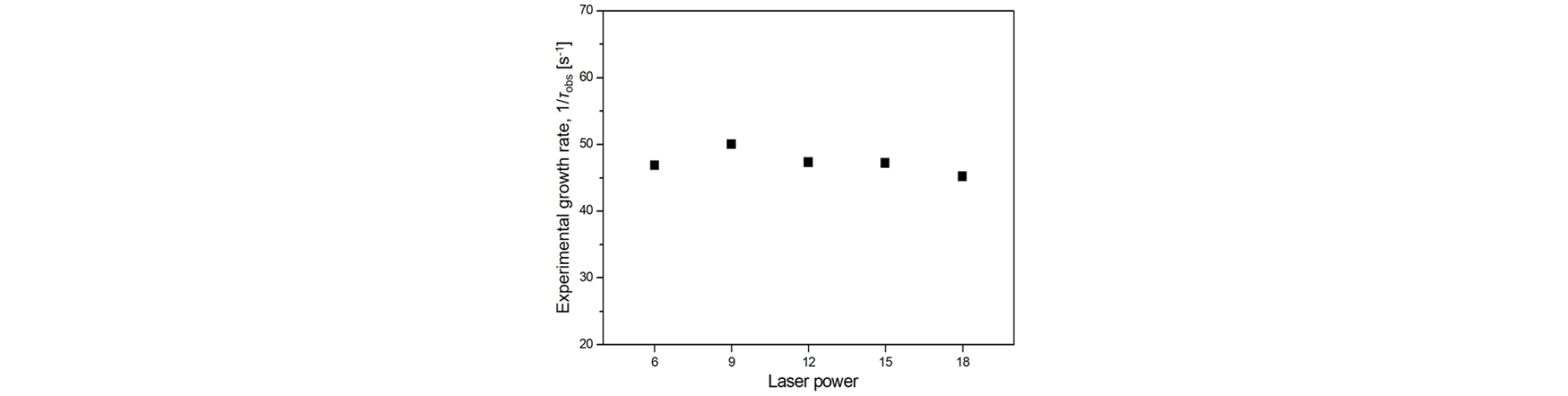
Fig. 7에 이차 열음향 불안정성의 압력 성장률(Fig. 4(b), 붉은 점선으로 표시된 기울기, τobs)을 레이저 출력 별로 도시하였다. 그림에서 알 수 있듯이 압력 성장률이 레이저 출력에 따른 화염 면적 변화가 상이함에도 불구하고 약 45 s-1로 일정한 값을 가지는 것을 알 수 있다.
상기의 실험 결과는 이전 연구결과[16], [17]의 주장에 위배되는 결과로서, 화염면적 변화 혹은 화염 면에 발생하는 파수가 이차 열음향 불안정성 성장 메커니즘(growth mechanism)에 미치는 영향이 크지 않다는 점을 내포하고 있다. 그럼에도 불구하고 레이저 조사 유무에 따라 레이저를 조사하지 않은 기본화염인 일차 열음향 불안정성에서 이차 열음향 불안정성으로 압력 증폭이 이뤄졌다는 점을 상기한다면 이차 열음향 불안정성 발생 메커니즘(onset mechanism)에서의 화염 면적 변화의 영향은 무시할 수 없을 것으로 판단된다.
이전 문헌[16], [17]에서 본 실험결과와 다른 결과가 도출된 원인으로 이전 실험에서는 수력학적 불안정성을 정량적으로 제어하지 않고 화염 표면에 자연스럽게 발생하는 셀의 파수를 측정하였고, 무작위(random)하게 발생되는 셀의 크기는 다를 수밖에 없다. 또한 본 연구실의 이전 연구[7]에서도 가스조성의 결합상수가 증가할수록 높은 압력 성장률이 도출되었는데 이 점을 미루어 볼 때, 이차 열음향 불안정성의 압력 성장률이 증폭하면 화염 표면에 발생하는 셀 불안정성이 심화되나, 이 명제의 역인 셀 불안정성의 성장률은 이차 열음향 불안정성의 압력 성장률에 무관하다는 것으로 이해할 수 있다.
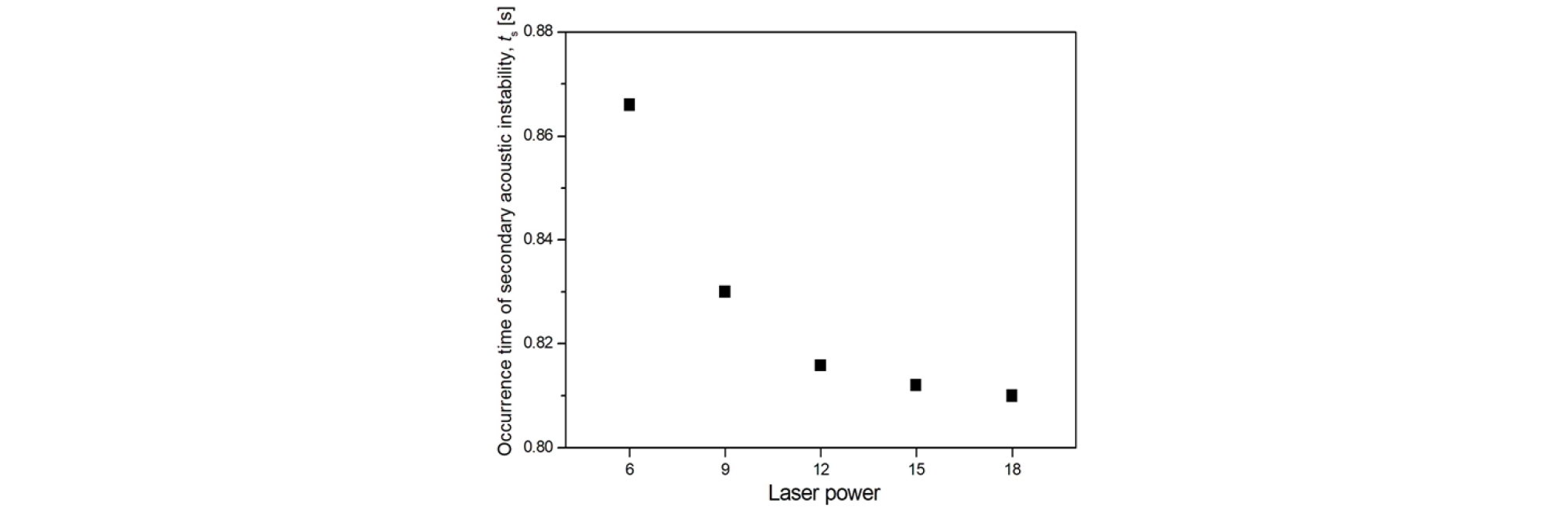
Fig. 8에 이차 열음향 불안정성의 발생 시점(Fig. 4(a), II-III)을 레이저 출력 별로 도시하였다. 그림에서 알 수 있듯이 레이저 출력이 증가함에 따라 이차 열음향 불안정성의 발생 시점이 빠르다는 것을 알 수 있고 이 점을 미루어 보아 높은 화염 면적 변화율에서 이차 열음향 불안정성의 발생이 상대적으로 용이하다는 결론을 획득할 수 있었다.
4. 결 론
본 연구는 CO2 레이저 조사기법을 채택하여 1/4파장 공명기 내 전파하는 예혼합 화염의 화염면적을 인위적으로 제어하여 화염 면에 발생하는 수력학적 불안정성의 강도에 따라 이차 열음향 불안정성에 미치는 영향에 대해 실험적으로 조사하였다. 이차 열음향 불안정성으로 천이하지 않고 일차 열음향 불안정성만 발생하는 기본 화염에 화염면적을 인위적으로 증가시킨 결과 이차 열음향 불안정성이 발생하였고, 높은 화염면적 변화율에서 이차 열음향 불안정성 발생 시점이 빠르게 나타났다. 하지만 압력 변동의 성장률은 화염면적 변화율과는 무관하게 일정한 값이 도출되었고 이 점을 미루어 보아 이전 문헌[16], [17]에서 주장하는 것과 같이 이차 열음향 불안정성의 성장 메커니즘은 화염면적 변화율에 비례하는 것이 아니라 다른 요인이 있을 것으로 판단되고 이는 향후에 추가 연구를 수행하여 규명하고자 한다.